多模型粒子滤波在机动目标跟踪中的应用

闫文利， 王建刚， 柳 毅

(光电控制技术重点实验室，河南洛阳 471009)

0 引言

由于双机协同无源跟踪能够提供飞机的隐蔽性，符合“静默”攻击的要求，使其成为近几年最广泛研究的跟踪技术之一。在以往的研究中，一般假设目标匀速执行运动或变速直线运动［1－2］，而空中运动的目标总是机动的，因此研究空中机动目标的跟踪具有很强的现实意义。

现有的机动目标跟踪算法中，由 Bolm和 Bar-Shalom提出的交互式多模型(Interacting Multiple Model，IMM)及其改进算法被广泛应用于跟踪机动目标［3－5］。该方法采用马尔科夫转移概率进行模型切换，对线性机动的目标达到很好的跟踪效果。目前主要采用交互式多模型(IMM)和扩展卡尔曼滤波相结合处理非线性问题［6－7］，由于扩展卡尔曼滤波(EKF)对非线性模型进行一阶线性化，这样不可避免地引入很大的线性误差，造成跟踪精度大大降低，甚至出现失跟现象，限制了交互式多模型的进一步发展。

近年来，许多学者将交互式多模型和粒子滤波相结合用以处理非线性问题，并取得很好的效果。文献［8］指出了交互式多模型方法和粒子滤波结合时存在的主要问题，并介绍了几个有价值的应用方向;文献［9］提出一种基于多模型粒子的多目标跟踪算法，有效地解决了密集杂波环境下机动多目标跟踪中的非线性问题。现有的文章基本都是对二维机动目标进行跟踪，本文在双机协同跟踪的基础上，将交互式多模型粒子滤波用于跟踪空中三维机动目标。最后通过仿真表明，该算法对空中三维机动目标跟踪效果优于扩展卡尔曼滤波和交互式多模型扩展卡尔曼滤波。

1 系统模型

考虑协同飞机与空中机动目标的几何关系，建立如图1所示的笛卡尔三维坐标系。其中:φ1和θ1为目标相对于飞机1的方位角和俯仰角;φ2和θ2为目标相对于飞机2的方位角和俯仰角。

图1 协同飞机与目标的几何关系Fig.1 The geometry of cooperative planes and target

其中:w(k－1)是以Q为协方差的非高斯过程噪声。

协同飞机在任意采样k时刻可以提供目标相对于该飞机的方位角和俯仰角信息，则该系统观测方程为

其中:Z(k)=［φ1(k)，θ1(k)，φ2(k)，θ2(k)］T，

其中:xP1(k)，yP1(k)，zP1(k)，xP2(k)，yP2(k)，zP2(k)分别表示k时刻飞机1和飞机2相对于坐标原点的距离在X，Y，Z坐标轴上的分量;v(k)是以R为协方差的高斯白噪声且与w(k－1)相互独立。由式(2)可知该系统的观测方程有很强的非线性。

2 粒子滤波

粒子滤波是通过蒙特卡罗法从后验概率随机抽取一组带权重的粒子集，用粒子集来逼近后验概率分布，并序贯地预测和更新。粒子滤波一经提出就成为解决非高斯非线性问题最热门的算法之一，如今已被广泛应用于目标跟踪［10］、信息处理［11］等领域。

假设已知目标状态的初始概率密度，并且已获取k－1时刻的概率密度p(X(k－1)/Z(k－1))，在式(1)和式(2)的基础上，则预测和更新过程为

理论上可通过式(3)和式(4)求取后验概率密度分布，但通常情况下积分的解析解很难获得。后验概率分布可以用有限个离散样本来近似，问题是通常很难直接从后验概率采样。为了解决这一问题，可以从一个已知的、容易采样的重要性函数q(X(k)/Z(k))采样一组粒子集来逼近后验概率密度分布，则粒子的重要性权值为

则后验概率的真实分布用式(6)逼近为

假设系统的状态是一个马尔科夫过程，且各次观测相互独立，由此得到重要性函数的另一种表达式为

从而得到重要性权值迭代公式为

可见重要性函数的选择至关重要，目前还没有一个广泛使用的重要性函数，先验概率分布是目前较常使用的重要性函数

顺序重要性采样是目前使用比较多的采样方法之一，但其缺点是随着时间的推移将出现粒子的退化现象。因此，文献［8］提出了重采样的方法来解决粒子退化问题，然而重采样又会造成粒子的贫化现象，为了恢复粒子的多样性，又引入了MCMC移动步骤算法，二者的结合基本解决了粒子的退化和贫化现象。

3 交互式多模型粒子滤波

交互式多模型粒子滤波是融合交互式多模型和粒子滤波算法的一种新算法。该算法充分发挥交互式多模型和粒子滤波各自的优点，既解决了机动目标跟踪过程中模型不匹配的问题又可对非线性非高斯问题起到很好的作用。假设模型转移概率矩阵Π={πij，i，j=1，2，…，M}，模型概率 U={ui，i=1，2，…，M}，M 为模型数。已知目标的初始状态Xi(0)，i=1，2，…，M和协方差Pi(0)，i=1，2，…，M。另外，该算法的每个模型采用固定数目的粒子。交互式多模型粒子滤波的主要过程如下所述。

1)随机采样粒子集。

在k(k＞0)时刻根据k－1时刻各个模型状态和协方差的均值随机采样各个粒子状态1，2，…，M，n=1，2，…，N 和协方差1，2，…，M，n=1，2，…，N，其中 N 为粒子个数。

2)输入交互。

各个模型间相应的粒子进行交互

3)滤波。

在输入交互的基础上每一个粒子匹配一个粒子滤波器对其进行滤波，根据式(1)和式(2)得到粒子的状态预测和观测预测为

粒子的重要性权值为

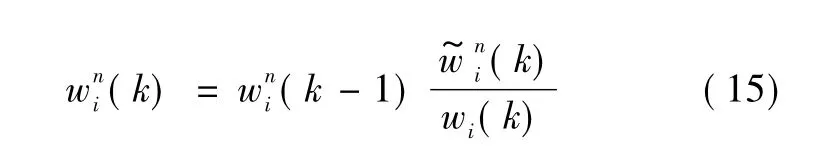
残差重采样。

4)模型概率更新。

各模型的似然函数为

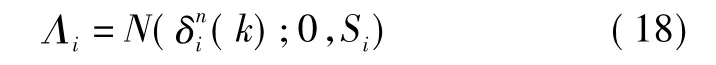
各模型概率更新为

5)输出交互。

对各模型进行输出交互得到状态及其协方差的估计值

4 仿真与分析

4.1 运动轨迹

在整个跟踪过程中两架协同飞机在做高度不变匀速直线运动，目标沿Z轴方向一直做匀速直线运动，在XOY平面上的运动有以下7个阶段:

1)0～20 s目标做匀速直线运动;

4.2 仿真结果分析

本文采用扩展卡尔曼滤波(EKF)、交互式多模型扩展卡尔曼滤波(IMMEKF)和交互式多模型粒子滤波(IMMPF)3种算法对空中机动目标进行跟踪。图2是目标运动的真实轨迹和EKF、IMMEKF、IMMPF算法的跟踪轨迹。

图2 目标运动真实轨迹和3种算法的跟踪轨迹Fig.2 The true trajectory of target and tacking trajectory of three algorithms

图3 为EKF、IMMEKF、IMMPF算法X位置的均方根误差;图4为EKF、IMMEKF、IMMPF算法Y位置的均方根误差;图5为EKF、IMMEKF、IMMPF算法Z位置的均方根误差。

图3 X位置均方根误差Fig.3 The root mean square error of X poistion

图4 Y位置均方根误差Fig.4 The root mean square error of Y poistion

综合分析图2～图5可以看出，在目标匀速直线运动阶段(0 ～20 s，30 ～50 s，60 ～80 s，90 ～100 s)IMMPF的跟踪性能与EKF和IMMEKF基本相同，甚至有些时候稍弱于后面二者;但在目标转弯机动阶段(20～30 s，50～60 s，80～90 s)IMMPF的跟踪性能明显优于EKF和IMMEKF;在目标从机动转为匀速直线运动后IMMPF收敛速度最快，IMMEKF次之，EKF最差;分析整个跟踪过程发现EKF和IMMEKF在目标直线运动时跟踪精度高，目标转弯机动时跟踪精度明显降低，而IMMPF基本不变，说明IMMPF有很强的鲁棒性。

图5 Z位置均方根误差Fig.5 The root mean square error of Z poistion

5 结论

本文在双机协同跟踪的基础上，将交互式多模型粒子滤波应用到对空中机动目标跟踪过程中，基本上解决了扩展卡尔曼滤波和交互式扩展卡尔曼滤波处理非线性问题的局限性。最后，通过仿真验证了交互式多模型粒子滤波的跟踪精度、收敛速度和鲁棒性等方面明显优于扩展卡尔曼滤波和交互式多模型扩展卡尔曼滤波。

［1］ 夏军成，王春波，倪天权.多舰协同定位算法［J］.舰船电子对抗，2008，31(3):71-73.

［2］ 孙仲康，周一宇，何黎星.单多基地有源无源定位技术［M］.北京:国防工业出版社，1996.

［3］ BLOM H A P，BAR-SHALOM Y.The interacting multiple model algorithm for systems with markovian switching coefficients［J］.IEEE Trans on Automatic Control.1988，33(8):780-783.

［4］ 顾潮琪，周德云，曲艺海.一种精确跟踪机动目标的滤波算法的研究［J］.电光与控制，2008，14(2):8-11.

［5］ 孙庆鹏，孔祥维，卢聪聪，等.用于非线性机动目标跟踪的新型 IMM 算法［J］.电光与控制，2008，15(8):14-19.

［6］ 朝磊，马晓莹.一种基于IMM-KF的机动目标跟踪算法［J］.数据通信，2009(3):66-68.

［7］ MAZOR E，AVERBUCH A，BAR-SHALOM Y，et al.Interacting multiple model methods in target tracking:As urvey［J］.IEEE Transactions on Aerospace and Electronic Systems.1998:34(1):103-123.

［8］ 周云锋，单甘霖，张淼.交互式多模型粒子滤波算法综述［J］.军械工程学院学报，2010，2(1):57-62.

［9］ 胡振涛，潘泉，杨峰，等.基于多模型粒子滤波的机动多目标跟踪算法［J］.四川大学学报，2010，42(4):136-141.

［10］ 沈玉娟，王健.基于粒子滤波跟踪方法研究［J］.仪表技术，2010(3):55-57.

［11］ GORDON N J，SALMOND D J，SMITH A F M.Novel approaeh to nonlin-ear/non-Gaussian Baye sianstate estimation［J］.IEE Proe.Radar and Signal Processing 1993，140(2):107-113.