地面移动目标被动探测最优路径规划

杜昌平， 刘 敏， 高瑞周， 陈哨东

(1.浙江大学航空航天学院，杭州 310027; 2.光电控制技术重点实验室，河南洛阳 471009;3.中航工业洛阳电光设备研究所，河南洛阳 471009)

0 引言

采用被动方式工作的无源定位技术具有作用距离远、隐蔽测量接收、不易被对方发觉的优点，对于增强系统在复杂电磁环境下的生存能力和工作能力具有重要意义［1］。另外，通过无源定位技术对已知地理位置的目标进行测量定位，可以确定飞行或运动中物体的空间位置，这在导航和制导定位中具有重要意义。由于无源定位系统自身无法获得距离信息，因此一般要多个观测站共同测量才能实现。但多站无源定位受到时间同步、数据通信传输、数据有效等约束，且机载平台又具有作用距离远、覆盖地域大、机动性好等优点，因此机载单站被动探测技术研究受到更多关注［2］。

目前国内外针对机载单站被动探测技术的研究已有一些相关的报道。研究成果主要集中在测角定位系统的非线性滤波方法方面［3－9］，在承载平台的机动运动方面的研究报道相对较少。文献［1］研究了分布式传感器跟踪三维运动目标的EKF方法;文献［2］提出了采用UKF滤波算法进行单传感器移动目标的定位和跟踪;文献［5］分析比较了单传感器测角定位系统的高斯和滤波(Gaussian Sum Measurement Approximation Filter)、LPC-EKF和RP-EKF滤波算法，提出了在仅测角定位的情况下，完全的目标信息不可测，指出了选择适当的量测计算坐标系和滤波模型对定位计算影响较大;文献［9］研究了适用于小型无人机的单光学传感器目标定位的轨迹规划方法，并在不同的目标运动状态下进行了仿真研究，指出了在适当的无人机机动下目标的定位精度将有较大提高。其轨迹规划不考虑承载平台自身性能约束及环境约束。从传感器测量目标状态的精度出发，采用扩展卡尔曼滤波算法进行传感器量测信息滤波，考虑目标被动探测的环境及飞行器性能约束，以目标量测信息阵等为指标，进行被动探测最优路径规划，实现地面移动目标探测，并进行了该被动探测最优路径规划算法的仿真研究。研究结果表明，所提出的被动探测最优路径规划算法能够快速、有效地完成最优被动探测路径的规划计算。

1 路径规划相关模型

首先，运用扩展卡尔曼滤波方法进行目标被动测量滤波，然后，计算目标探测跟踪的信息矩阵。被动目标探测传感器自身不辐射电磁、声、光等信号，通常只能获得辐射源目标的方向信息(角度信息)。且假设传感器测量噪声和目标运动系统噪声均为加性高斯白噪声，则系统模型如下所示。

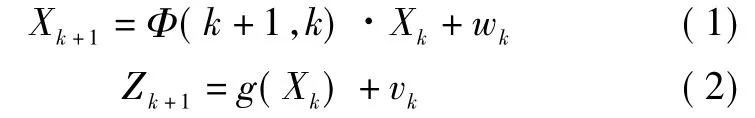
式中:Xk为k时刻系统状态，即目标的地理位置信息;Zk为k时刻系统测量信号;g(*)为非线性函数;wk为k时刻系统噪声;vk为k时刻测量噪声，且wk～N(0，Qk)，vk～ N(0，Rk)。则测量系统模型为

式中:xt，yt，zt为目标 k 时刻位置分量;xf，yf，zf为载机k时刻位置分量。

1.1 传感器目标量测信息阵模型

信息矩阵是衡量系统状态估计性能指标之一，且该信息阵具有便于工程计算的递推计算形式，以及多传感器量测和时间序列上的累加特性。因此，研究采用信息矩阵建立的光电传感器探测轨迹规划指标模型，所建立的光电传感器探测轨迹规划指标模型计算量小、计算速度快。同时，信息阵快速收敛的方向即为传感器对目标状态探测估计快速趋于稳定方向的衡量指标之一。信息矩阵定义为

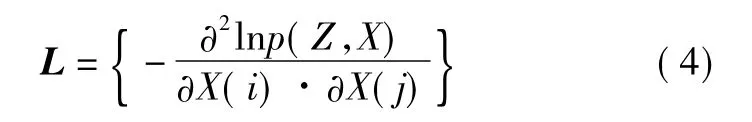
式中:p(Z，X)为系统状态X与系统量测值Z的联合概率密度函数;X(i)为第i个状态。

在上述传感器模型式(1)、式(2)和式(3)条件下，采用EKF滤波模型［1］进行传感器滤波计算，则传感器探测信息阵递推计算式为

1.2 传感器路径指标模型

光电传感器最佳探测轨迹规划算法以传感器最佳探测路径长度、传感器探测角度约束与传感器信息阵为指标，其传感器最佳探测轨迹规划指标计算模型为

式中:Fit为光电传感器最佳探测轨迹指标值;a1，a2，a3为各因素综合的权值;Lk为光电传感器目标探测信息阵，由式(5)计算;Mmax为传感器被遮挡下的探测目标信息值，max(diag(*))为取矩阵对角元素最大值函数;D为光电传感器规划路径长度;φm为目标方位角;θm为目标俯仰角;b1，b2为目标方位角、俯仰角综合加权值;exp(*)为指数函数;n为当前传感器规划路径的路径点个数;xi，yi，zi为传感器第 i个路径点位置分量值;Rfx，Rfy，Rfz为当前目标相对载机的机体系距离分量值。

2 探测轨迹规划算法

机载传感器对地面移动目标被动测量的最优路径规划方法，考虑目标被动探测的环境及飞行器性能约束，即进行目标量测信息阵计算时考虑探测遮挡，若遮挡则其数值不计算而直接设为指定值，否则按式(5)计算。遮挡计算和判断主要采用线、面几何相交计算模型，计算和判断当前载机传感器位置与运动目标，在当前位置间是否受到建筑物、地形等光电信号不可穿越威胁遮挡。同时，考虑飞行器的转弯、爬升和俯冲性能，可能的路径搜索方向则在转弯、爬升和俯冲性能约束范围内寻优计算。目标探测信息阵为衡量传感器探测目标精度的指标之一，该信息阵收敛方向，则为传感器探测目标快速收敛方向。故而以目标量测信息阵为指标，进行被动探测最优路径规划，实现地面移动目标探测。探测轨迹规划具体步骤如下:

1)初始化滤波参数、计算时间步长、角度步长、最优路径列表等相关参数;

2)滤波计算当前载机目标态势下的目标运动状态信息;

3)根据飞行器当前位置、状态和机动性能及载机路径搜索角度步长，确定和搜索机载传感器平台下一步可行的飞行方向;

4)计算当前可行方向下的载机传感器平台和目标相对态势信息;

5)根据当前载机、目标和威胁/环境信息，采用线面几何相交计算模型，计算分析机载传感器被动探测遮挡;

6) 按照式(5)、式(7)、式(8)、式(9)计算传感器信息阵值，计算当前可行路径长度及载机运动角度约束;

7)按照式(6)进行当前路径长度、载机运动角度约束与传感器信息阵加权综合;

8)判断所有可行方向是否计算完成，若未完成则返回3)，否则转9);

9)根据综合指标值，以指标值最小的可行方向确定为当前最优可行方向及路径段;

10)将当前最优路径段加入最优路径列表;

11)判断路径规划结束条件，若未结束则返回2)，否则转12);

12)输出最优路径列表，结束规划计算。

采用上述的载机传感器对地面运动目标的路径规划计算，并给出满足载机运动约束条件下的传感器探测指标快速收敛的可行的探测路径。

3 仿真结果及分析

采用机载传感器对地面移动目标被动测量的最优路径规划方法进行了算法仿真。取飞行器平均飞行速度250 m/s，最大水平机动角 9(°)/s，搜索步长为1.5°，最大俯仰机动角6(°)/s，搜索步长为1.2°，预测计算步数为5;目标为匀速直线运动，速度为12 m/s;无遮挡时初始飞机位置东向0 m，北向0 m，天向1500 m，目标位置东向－50 m，北向15000 m，天向0 m，遮挡时初始飞机位置东向－274 m，北向223 m，天向1500 m，目标位置东向－50 m，北向15000 m，天向0 m。图1、图2所示为仿真计算的部分结果。

传感器探测目标区域无遮挡物条件下的匀速直线运动目标最优探测路径规划结果如图1所示。其中:红色细曲线为探测路径(起点为左侧端点，终点为右侧端点);蓝色粗线段为目标运动轨迹(起点为左侧端点，终点为右侧端点)。目标区域有障碍物遮挡条件下传感器最佳探测路径规划结果如图2所示。图2a为路径在水平面的投影图，其中，绿色粗点线为探测路径(起点为左侧端点，终点为右侧端点)，蓝色细线段为目标运动路径(起点为左侧端点，终点为右侧端点)，红色曲线为遮挡物体水平面截面;图2b为规划路径的空间图，其中，S为路径起点，E为路径终点。结果表明，在存在遮挡条件下，路径能够规避遮挡，实现移动目标的连续探测和识别，且算法规划路径考虑了传感器平台角度机动约束，所规划的每一步均能满足飞行器角度机动性能约束。

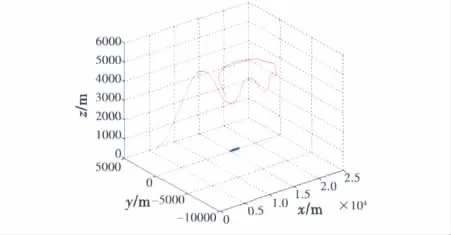
图1 目标匀速直线运动无遮挡的最优探测路径规划结果图Fig.1 Optimal path for detecting the constant velocity target without sheltering

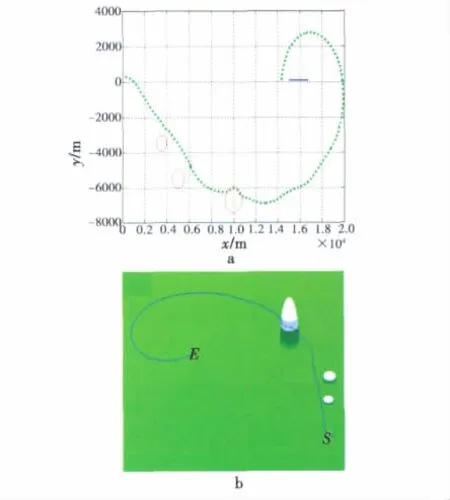
图2 目标匀速直线运动存在遮挡的最优探测路径规划结果图Fig.2 Optimal path for detecting the constant velocity target with sheltering

4 结论

本文提出了一种机载传感器对地面移动目标被动测量的最优路径规划方法。该方法从传感器测量目标状态的精度出发，采用扩展卡尔曼滤波算法进行传感器量测信息滤波，进而计算目标探测跟踪的信息矩阵。综合目标量测信息阵，考虑被动探测遮挡等，进行被动探测最优路径规划。所提出的算法以目标信息矩阵为基础，易于进行传感器量测数据的精度控制，且信息矩阵能够进行递推计算，计算速度快。综合信息阵等为路径规划算法的指标，并进行探测遮挡计算，能有效规避遮挡。本文进行了该被动探测最优路径规划算法的仿真研究。研究结果表明，文中提出的被动探测最优路径规划算法能够快速、有效地完成最优被动探测路径的规划计算。

［1］ MASAYOSHI I，SHINGO T，YOSHIO K.Tracking a threedimensional moving target with distributed passive sensors using extended kalman filter［J］.Electronics and Communications，2001，84(7):74-85.

［2］ XUE A，GUO Y.Bearings only target tracking with signal time delay using the IR PUKF algorithm［C］//The 6th International Conference on Intelligent Systems Design and Applications，2006:740-744.

［3］ CHEN X，SCHONFELD D，KHOKHAR A.Localization and trajectory estimation of mobile objects with a single sensor［Z］.SSP，2007:363-367.

［4］ RISTIC B，ARULAMPALAM M S.Tracking a manoeuvring target using angle-only measurements:algorithms and performance［J］.Signal Processing，2003(8):1223-1238.

［5］ LA S B，MORELANDE M.An analysis of the single sensor bearings-only tracking problem［C］//The 11th International Conference on Information Fusion，2008:1-6.

［6］ MUSICKI D.Bearing only single-sensor target tracking using Gaussian mixtures［J］.Automatica，2009(45):2088-2092.

［7］ CLARK J M C，VINTER R B，YAQOOB M M.The shifted rayleigh filter for bearings only tracking［C］//The 8th International Conf.on Information Fusion，PA，USA，2005:2131-2138.

［8］ CLARK J M C，VINTER R B，YAQOOB M M.The shifted rayleigh filter:A new algorithm for bearing only tracking［J］.IEEE Transactions on Aerospace and Electronic Systems，2007(10):1373-1384.

［9］ PONDA S S，KOLACINSKI R M，FRAZZOLI E.Trajectory optimization for target localization using small unmanned aerial vehicles［C］//AIAA Guidance Navigation and Control Conference，AIAA-2009-6015:1211-1235.