基于改进遗传算法的UAV航迹规划

鲁 艺， 吕 跃， 罗 燕， 张 亮，， 赵志强， 唐 隆

(1.空军工程大学工程学院，西安 710038; 2.中国人民解放军95183部队，湖南 邵阳 422000)

0 引言

无人飞行器(Unmaned Air Vehicle，UAV)作为一种新型作战武器，必将会以其特有优势越来越多地应用于未来战争中。作为UAV的关键技术之一，航迹规划问题已受到国内外学者的广泛研究，但目前关于最优航迹求解问题，大多是将某条整体代价最小航迹作为最优航迹，而没有求解出航迹上航迹点的杀伤概率［1－2］，这样可能导致的问题是:即使某条航迹整体代价最小，但可能会出现局部航迹点的杀伤概率无法满足UAV的安全性要求，因此所得到的最优航迹并不是真正意义上的最优航迹 。文献［3－4］将火力杀伤区分为完全杀伤区和概率杀伤区，利用分水岭算法求解出了最优航迹，但仍然没有求解出航迹点的具体杀伤概率，因此所求航迹在实际作战环境中也不一定是可行航迹。

本文首先在利用骨架化算法得到规划搜索空间的基础上，建立了雷达探测威胁和地空导弹杀伤威胁共同作用下的杀伤概率模型，求解出了规划搜索空间中航迹点的杀伤概率和航迹段的威胁代价。然后利用本文设计的遗传算法找到代价最小、次小、第三小等航迹，并根据本文提出的航迹选取原则，选择出真正意义上的最优航迹。

1 骨架化算法的规划空间建模

规划空间建模作为航迹规划的关键技术之一，是建立航迹代价函数和进行航迹寻优的基础和依据。数字高程地图作为记录地形、地貌和地面威胁空间分布的工具，是航迹规划的信息来源和计算依据。本文中采用某100 km×100 km的数据高程地图，首先将其均匀离散化201×201的网格点，两个相邻网格点之间的垂直或水平距离为500 m。然后进行数字高程地图的二值化，规定图像矩阵中“0”为背景，“1”为前景，该地图在某高度的地形威胁二值图像如图1所示。

图1 地形威胁图像Fig.1 Image of terrain threats

在实际作战环境中，除地形威胁外，还存在雷达探测威胁和火力杀伤威胁。本文假定地面火力威胁均为地空导弹杀伤威胁。地空导弹杀伤区可分为完全杀伤区和概率杀伤区。完全杀伤区可简化为一系列在水平投影上不可穿越的黑色圆形区域，概率杀伤区的杀伤概率随着UAV与地空导弹距离的增大逐渐变小。将地空导弹杀伤威胁与地形威胁图像叠加可得到综合威胁图像，如图2所示，图中的黑色圆形区域表示地空导弹的完全杀伤区，完全杀伤区实际上等效于地形威胁。

图2 综合威胁图像Fig.2 Image of compositive threats

对于如图2所示综合威胁图像，采用骨架化算法［5－6］生成如图3所示规划搜索空间，将规划搜索空间与综合威胁图像相叠加，可得到综合威胁图像与规划搜索空间的叠加图像，如图4所示。

图3 优化后规划搜索空间Fig.3 The planning space after optimuization

图3 和图4中，S为UAV的起始点;T为UAV的目标点，分别用★和▲表示。

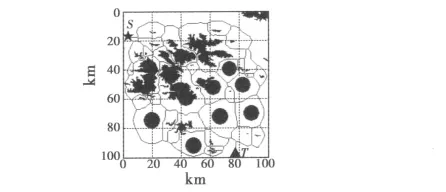
图4 威胁与规划搜索空间叠加Fig.4 Combination of threats and planning space

规划搜索空间实际上是由一系列航迹段、航迹点和节点组成。提取规划搜索空间中的信息，将航迹节点信息存储于二维矩阵node(node_num，8)中，边(航迹段)的信息存储于二维矩阵way(way_num，10)中，航迹点的信息存储于Route_point三维矩阵中［7］。

2 航迹代价函数建立

航迹代价函数建立是航迹规划中一个基本而又重要的组成部分。建立航迹代价函数时，需综合考虑影响航迹代价的各项因素，进而确定影响航迹代价的指标和权重。

1)通过骨架化算法得到了规划搜索空间，对于规划搜索空间中的任意航迹段，其燃油代价记为 Jfuel，i［2］。文献［8－9］分别建立了雷达探测概率模型和地空导弹杀伤概率模型，但实际上雷达和地空导弹是相互联系的，地空导弹打击目标在雷达发现目标的前提下进行，因此应该建立雷达探测威胁和地空导弹杀伤威胁共同作用下的杀伤概率模型。

本文假设地空导弹和雷达为一体。结合系统，N部雷达发现目标相互独立，发现目标的概率分别为P(R1)，P(R2)，…，P(RN)(N ＞0)，则 N 部雷达共同作用下对目标的探测概率为

设Q部地空导弹在N部雷达作用下对目标的杀伤概率分别为 P(M1|R)，P(M2|R)，…，P(MQ|R)(Q ＞0)，则N部雷达共同作用下，单部地空导弹对目标的杀伤概率分别为P(M1R)，P(M2R)，…，P(MQR)，则应用全概率公式［10］可求得Q部地空导弹和N部雷达共同作用下对UAV的杀伤概率为

对于规划搜索空间中任意航迹点和航迹段，都可利用式(1)和式(2)求解出其在多部地空导弹和多部雷达共同作用下航迹点的杀伤概率和航迹段的威胁代价，航迹点的杀伤概率记为p，航迹段的威胁代价记为fthreat，i。

2) 求出燃油代价 Jfuel，i和威胁代价 fthreat，i后，可将航迹代价函数简化为

式中:J表示航迹的总代价;ω1，ω2分别表示燃油代价和威胁代价的权值，取值范围为［0，1］，且 ω1+ω2=1。

3 遗传算法航迹寻优

遗传算法(Genetic Algorithm，GA)属于仿生算法，是一种基于生物自然选择与基因遗传学机理的随机搜索算法，具有并形搜索、全局最优等优点［11］。

3.1 基因编码方式

由于所求航迹的航迹段个数不确定，因此本文采用变长度的基因编码方式，如图5所示。

图5 染色体结构Fig.5 The configuration of chromosone

图中:mi为当前节点的序列码;(xi，yi，zi)为当前节点的空间坐标信息;fi为当前节点的适应值(即当前节点到下一个节点的代价值);n为染色体的最大长度;N为染色体的实际基因的长度;F为该条染色体的航迹代价信息。

已知规划搜索空间中节点和边的信息，因此在进行基因编码时采取特殊的编码方式，具体步骤如下:

1)首先随机产生从1到node_num之间的随机数N，将其作为染色体结构的终点，连同与之相关的坐标信息填入相应的基因位，规定终点的适应值fN为0;

2)根据选定的起点信息和node(node_num，8)矩阵中node_num值的大小，连同与之相关的空间坐标信息、适应值信息填入染色体基因位的第1位;

3)根据way(way_num，10)矩阵中的信息，从前往后依次对每一条染色体的第2位至第(N－1)位进行填写，每个基因位对应1个节点，每个节点周围可能存在有1个节点、3个节点和4个节点3种情况，对于当前节点，其下一位节点信息分别按照这3种情况取均等概率填写;

4)填写完所有基因位后，由前至后将每一基因位的适应值相加填入染色体的最后一位，作为总的适应值F。

与文献［11］中的基因编码方式相比，采用这种染色体结构编码方式在赋值阶段的时间消耗会比随机赋值时间消耗稍多，但在进化时却能够节省很多时间，从而提高了航迹寻优的效率。

3.2 航迹评价

采用这种特殊的基因编码方式后，航迹评价就不用设置复杂的罚函数，只需遵循一条准则:适应值小的航迹优于适应值大的航迹。

3.3 进化算子的设计

由于采用了基于ERP算法［11］的特殊基因编码方式，因此本文设计了1个交叉算子和5个变异算子。包括交叉算子、扰动算子、插入算子、删除算子、交换算子和平滑算子［7］。

3.4 算法描述

采用遗传算法进行航迹规划时，系统首先为无人机生成大小为P的种群，完成初始化。然后按照图6所示进行航迹寻优。

图6 遗传算法流程图Fig.6 The flow chart of genetic algorithm

3.5 航迹选取原则

在实际作战环境中，UAV总会受到地空导弹的攻击，如果长期暴露在杀伤威胁区，必然会增大UAV被地空导弹击毁的概率，为此提出实际作战环境中的航迹评价原则:UAV在不同杀伤概率下沿某航迹飞行时所允许连续穿越的航迹点个数，不能超过保证其安全的最大航迹点个数，如表1所示。

表1 无人机在不同杀伤概率下的连续最大航迹点数目Table 1 The maximum number of route points for different kill probability

本文在采用遗传算法寻找到整体航迹代价最小、次小、第三小等航迹的同时，描绘出对应航迹上航迹点的杀伤概率分布图，因而对于所求航迹，均可通过表1和航迹所对应的杀伤概率分布图对其进行选取，判别其在实际作战环境中是否为可行航迹。

3.6 航迹平滑

航迹平滑是在航迹寻优的基础上，对寻优结果进行平滑处理［3］。航迹平滑前后航迹上航迹点位置的变化必然引起杀伤概率的变化，为确保无人机安全性，得到最优可飞航迹，本文提出航迹平滑的3个原则:

1)平滑后的航迹要满足无人机机动性能要求;

2)平滑后的航迹要满足无人机的安全性要求;

3)步长选取应以平滑后的航迹代价最小为原则。

4 仿真分析

4.1 仿真情况1

仿真情形1为利用遗传算法求解最优航迹。

采用图2中所示的综合威胁图像，根据式(3)中的航迹代价函数，在Matlab 2009环境下进行仿真分析。

参数设置:

1)雷达的最大探测距离Rmax=20 km，地空导弹完全杀伤区半径L0=6km，最大杀伤区半径Lmax=20 km;

2)P=100，S=60，即种群的大小为 100，每次迭代取60条航迹进行进化操作;

3)无人机起点坐标为(18 km，5 km)，终点坐标为(100 km，80 km)，在图中分别用★和▲表示;

4)所有的进化算子以1/6的概率选取;

5)最大进化代数为100代;

6) 燃油代价权值 ω1=0.7，威胁代价 ω2=0.3。

遗传算法的进化曲线如图7所示。

图7 遗传算法时的进化曲线Fig.7 The evolutionary curve of GA algorithm

图8 ～图10所示分别为整体代价最小、次小和代价第3小航迹，具体航迹代价值和不同杀伤概率下的不可行航迹点数目见表2。

表2 各航迹的代价值和不满足杀伤概率点的个数Table 2 The cost of route and the number of unfeasilble points

由图7可知，采用本文设计的遗传算法，在初始化完成后，就形成可行航迹。进化到20代左右时，形成接近全局最优航迹;进化到60代左右时，形成代价最小航迹。

图8 代价最小航迹及航迹点杀伤概率分布Fig.8 Route of the minimum cost and the kill prdoability of route points

图9 代价次小航迹及航迹点杀伤概率分布Fig.9 Route of the seconed minimum cost and the kill probability of route points

由图8～图10和表2可知，利用遗传算法进行航迹寻优，不仅可以找到代价最小航迹，而且还可以找到代价次小和第三小等航迹。

但代价最小和次小航迹不满足表1中UAV的安全性要求，故此时将代价第三小航迹作为真正意义上的最优航迹。

4.2 仿真情形2

仿真情形2为航迹平滑。

针对仿真情形1所得到的最优航迹，选择步长L=3为单位进行平滑处理。

图11所示为步长L=12时平滑后的航迹和其上航迹点的杀伤概率分布。表3所示为不同步长L平滑后的归一化航迹代价及不同杀伤概率下的最大连续不可行航迹点个数。

图10 代价第三小航迹及航迹点杀伤概率分布Fig.10 Route of the third minimum cost and the kill probability of route points

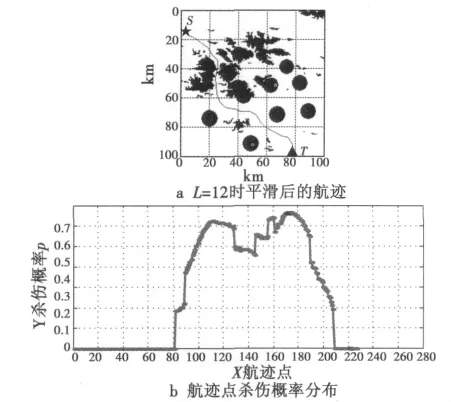
图11 L=12时平滑后的航迹及航迹点的杀伤概率分布Fig.11 The smoothed route when L=12 and the kill probability of route points

表3 平滑后的航迹代价及不同杀伤概率下连续不可行航迹点个数Table 3 The cost of smoothed route and the number of unfeasible points on different kill probability

仿真结果表明:各种步长条件下平滑后的航迹均满足无人机的安全性要求。当步长从L=3增大时，燃油代价和威胁代价均逐渐减小，整体代价也逐渐减小;当步长L=12时，整体代价最小。但随着步长进一步增大，燃油代价仍逐渐减小，威胁代价逐渐增大，整体代价却逐渐增大，所以将步长L=12时平滑的航迹作为最优航迹。因此，图11a中所示航迹为平滑后的最优可飞航迹。

5 小结

为实现实际作战环境中的UAV航迹规划，本文设计了一种基于特殊编码方式的改进遗传算法，不仅得到了最优可飞航迹，而且提高了航迹规划效率，具有实际作战意义。

本文首先采用骨架化算法生成规划搜索空间，在简化作战环境同时得到了贴近实际的规划搜索空间，并详细获知了规划搜索空间中的信息。其次，建立了雷达和地空导弹共同作用下的杀伤概率模型，求解出了规划搜索空间中航迹点的杀伤概率和航迹段的威胁代价。第三，采用本文设计的遗传算法进行航迹寻优，并根据航迹选取原则和平滑原则得到了实际作战环境中的可飞航迹。

［1］ 李季，孙秀霞.基于改进A_star算法的无人机航迹规划方法研究［J］.兵工学报，2008，29(7):788－792.

［2］ 赵文婷，彭俊毅.基于VORONOI图的无人机航迹规划［J］.系统仿真学报，2008，18(S2):159－165.

［3］ 杨新勇.基于分水岭算法的无人机航迹规划研究［D］.西安:空军工程大学，2009.

［4］ 穆中林，周丽丽.分水岭分割算法的飞行器低空突防航路规划［J］.电光与控制，2009，16(12):43－45.

［5］ 田岩，彭复员.数字图像处理与分析［M］.武汉:华中科技大学出版社，2009.

［6］ 穆中林，鲁艺.基于改进A*算法的无人机航迹规划方法研究［J］.弹箭与制导学报，2007，27(1):297－300.

［7］ 张亮.基于生存原则的无人机航迹规划方法研究［D］.西安:空军工程大学，2010.

［8］ 徐正军，唐硕.基于改进遗传算法的飞行航迹规划［J］.宇航学报，2008，29(5):1540－1544.

［9］ 郭锡福，赵子华.火控弹道模型理论及应用［M］.北京:国防工业出版社，1997.

［10］ 盛骤，谢式千.概率论与数理统计［M］.北京:高等教育出版社，2003.

［11］ 丁明跃，郑昌文，周成平，等.无人飞行器航迹规划［M］.北京:电子工业出版社，2009.