无人机视觉辅助着陆中的姿态和位置估算

李 飞， 唐大全， 沈 宁， 尹洪伟， 唐 波

(1.海军航空工程学院，山东烟台 264001; 2.中国人民解放军92514部队，山东烟台 264001)

0 引言

据资料统计，无人机回收阶段的故障数占整个任务执行阶段故障数的80%，因此无人机着陆导航技术受到广泛关注。由计算机视觉发展起来的视觉辅助导航方法，具有精度高、不受电子干扰等特点，因此在无人机的着陆导航中受到越来越多的关注［1］。视觉辅助导航方法主要是通过安装在飞机上的摄像机，获得着陆点附近的图像，使用计算机视觉算法，估计飞机的飞行状态和相对于着陆点的位置和方位，结合其他机载传感器的信息，实现无人机的自主着陆控制。

目前在利用视觉进行着陆的研究中，研究最多的是提取跑道边缘线和地平线等线特征来估算飞机的姿态和位置［2－6］。然而在战时，公路等简易机场都可以作为无人机的着陆场，这时候，地平线的提取易受建筑物、高山等地形的影响，跑道边缘线的提取容易受河流、公路等具有线特征地物的影响。

为了克服这些缺点，本文寻找易辨识的特征。特殊标识的点在图像中较容易辨识，这些点在夜晚可以是布置在跑道附近的灯光点，白天可以布置特殊形状的物体或者提取跑道附近特殊图案的角点;然后寻求地面上的点和图像上的点之间的对应关系，结合计算机视觉算法，提取出无人机着陆需要的相对跑道位置信息和姿态信息，同时结合最小中值法提高了精度。

1 坐标系及坐标变换

1.1 方程坐标系介绍

在本文的研究中用到跑道坐标系、机体坐标系、摄像机坐标系，3个坐标系之间的关系如图1所示。

各坐标系的定义如下。跑道坐标系P:ZP轴沿跑道中心线指向进场方向;XP轴在跑道平面内，与ZP垂直且指向右;YP轴垂直跑道平面且向下。

图1 几种坐标系之间的关系Fig.1 The relation among the coordinate systems

摄像机坐标系C:摄像机固联在飞机上，坐标原点为光学中心;ZC为光轴方向;XC垂直于飞机对称面指向飞机右侧;YC由笛卡儿右手系决定。为了论述方便，假设摄像机系和机体系是重合的。

1.2 坐标系变换

如何将跑道坐标系中的特征点投影到成像平面，是研究的基础，这个投影过程分为以下两步。

1)跑道坐标系向摄像机坐标系的变换，公式为

其中:旋转矩阵R由3个姿态角组成;平移矩阵D由飞机相对跑道的位置构成。

2)摄像机坐标系向图像坐标系变换近似为小孔成像。图像坐标系的原点O1为光轴与图像平面的交点;f为焦距;(x，y)为摄像机系中参考点在图像上的投影坐标。则有投影公式为

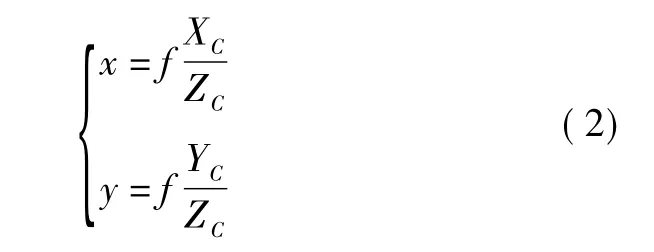
2 飞机姿态位置解算

下面将分两步解算飞机的姿态和位置:第一步求出特征点在摄像机系中的坐标［7］;第二步根据摄像机坐标及其对应的跑道坐标系坐标，解算出飞机的姿态和位置［8］。

2.1 解算特征点在摄像机坐标系中的坐标

假设已知3个特征点在跑道系和图像系上的坐标。

图2 3个特征点的几何图形Fig.2 The geometry figure of 3 feature points

3个特征点在摄像机系中坐标。dij(i，j=1，2，3)为这3个特征点在跑道系中的对应距离，根据图2中的对应关系，有并且参考式(2)(为了表述方便，这里用Xi代替，等式便可写成

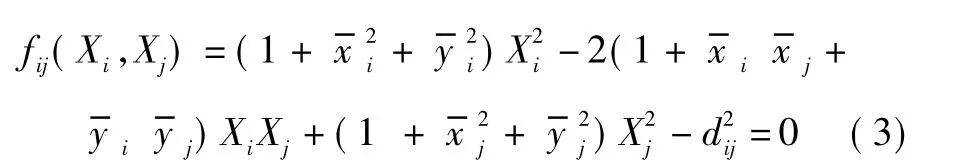
对于N=3个点，有

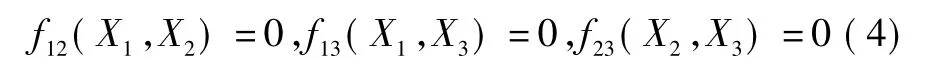
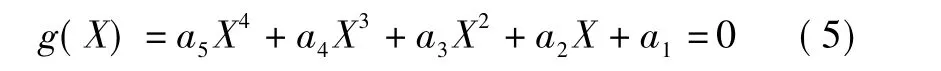
对于此多项式方程，最多有4个解。如果得到唯一解，根据X1是正数，可以将其唯一确定，然后根据式(2)便可确定其他两个坐标值。

为了得到唯一解需要再多增加几个点。对于N个点，能够得到(N(N－1))/2个fij(Xi，Xj)=0，进而得到((N－1)(N－2))/2个四次方程g(X)=0。

对于N=4，得到3个诸如式(5)的等式，写成矩阵形式

令 t5=(t0，t1，t2，t3，t4)=(1，X，X2，X3，X4)T，则方程(6)可看作齐次线性方程组。对该齐次线性方程组运用奇异值分解的方法［9］便可求得唯一解。

同样对于任意N≥5个点，都可以获得如式(6)形式的齐次线性方程组，再利用奇异值分解的方法即可求得唯一解。

2.2 解算飞机姿态位置

由于飞机的姿态和位置构成了旋转矩阵R和平移向量D，因此可以通过求出R和D得出飞机的姿态和位置。首先利用正交化算法［8］。假设跑道上3个点P1，P2，P3，在摄像机坐标系对应坐标为 C1，C2，C3。记为

显然，Up=(rp1，rp2，rp3)和 Uc=(rc1，rc2，rc3)是正交阵，于是，其中

在实际成像过程中，往往存在成像噪声，一些点的误差可能大于两三个像素，甚至会出现匹配误差，如果直接利用这些匹配点将产生较大的误差，鲁棒性会很差。根据文献［10］，将最小中值法用于计算旋转矩阵和平移向量可以大大提高算法的鲁棒性。

下面以4点算法为例，对最小中值法进行阐述。

1)从图像平面上的点(1，2，…，n)中随机选出4个点，例如，J=(1，2，3，4)。

2)利用4点定位算法求得这4个点在摄像机系中的坐标，并由图像匹配给出对应的跑道系坐标。

3)重复1)～2)，得出第k种随机点样本组合的跑道系坐标和摄像机系坐标。假设共取m个样本组合。

4)取出3)中m种样本组合的第k种。4个点对为(P1，P2，P3，P4)，(C1，C2，C3，C4)，在这 4 个点中，任取3个点进行组合，共有4种组合，如第1种点对的组合为(P1，P2，P3) 和(C1，C2，C3)，若(P1，P2，P3) 和(C1，C2，C3)中的一组3个点共线或接近共线，则舍弃不用，否则对(P1，P2，P3)和(C1，C2，C3)使用正交化算法求出旋转矩阵和平移向量，4种组合解算完毕求出没有舍弃的组合的平均值RJ和DJ。

5)计算残差平方为

6)计算中值为

3 卡尔曼滤波方法的应用

已知系统状态为:X(k)=［Xb，Yb，Zb，Vx，Vy，Vz，ψ，ϑ，γ，r，q，p］T，(Xb，Yb，Zb)为飞机在跑道坐标系中的位置;(Vx，Vy，Vz)为飞机在横向、垂直、纵向的速度;(ψ，ϑ，γ)为飞机的航向角、俯仰角、滚转角;(r，q，p)为横滚角速度、俯仰角速度、偏航角速度。滤波测量量由第2节求得的飞机姿态和位置给出:Z(k)=［Xb，Yb，Zb，ψ，θ，γ］T。飞机的位置从某一时刻到下一时刻的系统转移关系为

飞机的姿态角与上一时刻姿态角和转动角速度的关系为

由式(12)和式(13)可以得出系统的状态转移矩阵。

在得到了上述条件和飞机的初始时刻参数后，应用卡尔曼滤波方法［11］，就可得到每个时刻飞机的姿态和位置。

4 仿真与分析

参考国际民航组织精密进场着陆Ⅲ级精度要求，提出无人机着陆导航系统导航精度要求:到达着陆点时，垂直精度高于1.97 m;横向精度高于13.45 m。由于跑道长1000 m，所以对于纵向的位置偏差并没有做要求。俯仰角精度高于0.5°，滚转角精度高于0.5°，航向角精度高度高于0.5°。

4.1 仿真条件

构建20个随机点，这些点在沿跑道横向服从均值为0，标准方差为100的正态分布，在沿跑道纵向0～1000 m内服从均匀随机分布，并且假设在点匹配过程中存在两对错误匹配点。

飞机初始下滑高度为60 m，距离跑道起点纵向距离为1000 m。飞机下滑角为－3°，摄像机光轴与飞机纵轴夹角3°，且在飞机纵轴下方，下滑速度为40 m/s。系统噪声方差阵为对角阵，前6 个对角元素为［2，2，2，0.25，0.25，0.25］，后6 个对角元素均为(0.5π/180)2。测量噪声方差阵为对角阵，对角元素为［5，5，5，(0.5π/180)2，(0.5π/180)2，(0.5π/180)2］。

4.2 仿真结果分析

基于上述仿真条件，使用MatlabR2009a软件进行仿真，取N为4，即针对4点算法情况进行仿真，着陆导航信息误差图见图3和图4。

图3 位置估计误差Fig.3 The position estimation error

图4 姿态估计误差Fig.4 The attitude estimation error

由图3可知，对着陆安全性要求最高的横向位置误差基本能够控制在5 m以内，尤其是当距离机场越近时，误差越小，20 s后，距离机场纵向距离为201 m，横向误差基本在2 m以内;高度误差基本控制在1.5 m以内，20 s后，距离地面高度在18 m，高度误差控制在0.5 m以内;纵向误差维持在10 m以内。由图4可知，俯仰角的误差精度基本控制在0.5°内，尤其进入10 s后，精度达到 0.2°以内，进入 20 s后，精度达到 0.1°以内;偏航角在仿真开始时误差较大，但随着距离机场越近时，误差逐渐减小，进入20 s后，精度达到0.2°;滚转角始终保持在0.5°的精度范围。综上所述，本文所提算法满足无人机着陆要求。

最小中值法对于提高算法的鲁棒性至关重要，文章对最小中值法和常用的最小二乘法的效果进行了对比。两种方法的方差对比结果如表1和表2所示。由表1和表2可知，最小中值法解算出的导航信息的精度要远大于最小二乘法，究其原因，主要是噪声和错误匹配点的影响，最小二乘法假设噪声是高斯分布的，这是合理的，因为点的误差往往在一两个像素之内，但是有一些点可能没有很好地提取或者存在错误匹配，其误差要远大于两三个像素，这些点将严重影响导航信息估计的精度;而最小中值法能够排除误差较大的那些匹配点，由于仅考虑残差的中值，理论上即使有接近50%的错误数据，最小中值法都能给出精度很高的导航信息估计。

表1 位置误差方差对比Table 1 The contrast of position error variance

表2 姿态误差方差对比Table 2 The contrast of attitude error variance

此外，文章还对N为5的情况进行了实验仿真，即5点算法的情况。通过分析，使用4点算法解算一帧图像平均耗时52 ms，而使用5点算法解算一帧图像平均耗时320 ms，对于实时性要求很高的无人机着陆，5点算法不可取。

5 结束语

针对无人机在公路等简易机场着陆的情况，分析了线特征作为着陆辅助特征的缺点，并选取点特征进行辅助降落，运用N点算法和正交化算法求出了飞机的姿态和位置，考虑到噪声的影响，引入最小中值法和卡尔曼滤波法提高了算法的精度。通过仿真验证了文章所提算法解算出的位置和姿态均能满足着陆导航要求，并且通过对比分析了最小中值法对提高鲁棒性的作用，最后通过实验，发现5点算法的实时性无法满足着陆要求。

在公路等简易机场上，基于辅助特征点的视觉着陆在本文中得到了探索，为无人机视觉着陆的研究提供了一种新的思路。

［1］ 陈海.无人机自主控制综述及自主着陆控制系统设计［D］.西安:西北工业大学，2007.

［2］ PAN Xiang，MA Deqiang.Vision-based approach angle and height estimation for UAV landing［C］//IEEE Congress on Image and Signal Processing，2008:801-805.

［3］ LIU Tianshu，FLEMING G.Videogrammetric determination of aircraft position and attitude for vision-based autonomous landing［C］//The 44th AIAA Aerospace Sciences Meeting and Exhibit，2006，1437:1-35.

［4］ 朱宪伟，李由.机载视觉自主着陆过程中的跑道提取方法［J］.国防科技大学学报，2009，31(2):20-24.

［5］ TRISIRIPISAL P，PARKS M R.Stereo analysis for visionbased guidance and control of aircraft landing［C］//44th AIAA Aerospance Sciences Meeting and Exhibit.Reno，Nevada，2006，1438.

［6］ 陈龙胜，陈谋，姜长生.基于视觉信息的无人机自主着陆过程姿态和位置估计［J］.电光与控制，2009，16(5):47-51.

［7］ 马颂德，张正友.计算机视觉［M］.北京:科学出版社，1998:53-56，159-162.

［8］ QUAN Long，LAN Zhongdan.Linear N-point camera pose determination［J］.IEEE Transactions On Pattern Analysis And Machine Intelligence，1999，21(8):774-780.

［9］ 陈祖明，周家胜.矩阵轮引论［M］.北京:北京航空航天大学出版社，1998:192-195.

［10］ GHYZEL P A.Vision-based navigation for autonomous landing of UAV［D］.Naval Postgraduate School，2000.

［11］ 付梦印.Kalman滤波理论及其在导航系统中的应用［M］.北京:科学出版社，2010.