中考数学组合型开放题探析
2012-08-27江苏省靖江市第三中学沙咏蕾
☉江苏省靖江市第三中学 沙咏蕾
“体现新课标,提供新材料,追求新创意,提出新问题”是近年各省市中考数学命题的新特征.组合型开放题因能较好地反映这些新特征而备受命题者的青睐.所谓组合型填空题,就是给出若干个论断要求学生将其重新组合,使其构成符合题意的命题.解这类题,要求学生对所学的知识点间的关系有一个透彻的理解和掌握,通过对题目的阅读、理解、分析、比较、综合、抽象和概括,用归纳、演绎、类比等推理方法准确地阐述自己的观点,理清思路,进而完成组合顺序.这种组合型开放题,已使几何的论证转向发现、猜想和探究,从而促进学生生动活泼、主动的学习,并使中考试题充满活力和魅力,它对今后的课程改革将起着一个良好的导向作用.
下面从近几年的中考试卷中撷取几例,加以分析,供读者参考.
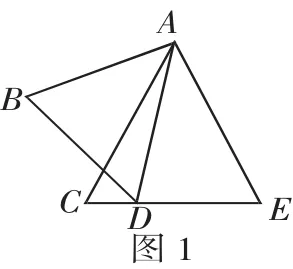
例1 如图1,在△ABD和△ACE中,有下列四个论断:①AB=AC;②AD=AE;③∠B=∠C;④BD=CE.请以其中的三个论断作为条件,余下一个论断作为结论,写出一个真命题是____(用序号的形式写出).
答案:可以构成四个命题:①②③⇒④;①③④⇒②;①②④⇒③;②③④⇒①.其中两个是正确的,两个是错误的,填写一个正确的命题是:①③④⇒②(或①②④⇒③).
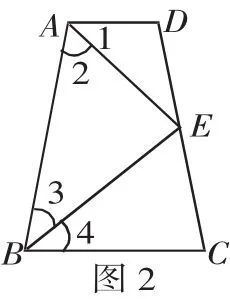
例2 如图2,四边形ABCD中,点E在边CD上,连接AE、BE,给出下列五个关系式:①AD∥BC;②DE=CE;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB.将其中的三个关系式作为题设,另外两个作为结论,构成一个命题.
(1)用序号写出一个真命题(书写形式为:如果×××,那么××),并给出证明;
(2)用序号再写出三个真命题(不要求证明);
(3)加分题:真命题不止以上四个,想一想,就能够多写出几个真命题,每多写出一个真命题就给你加1分,最多加2分.
评析:本题是一道条件和结论都开放的综合型组合题,充分考查了学生对几何知识点的整合能力,洞察能力和证明过程的严密性.解答此题既是一个再学习的过程、一个探索的过程、一个用数学的过程,又是学生展示能力和实力的过程,它对学生能力要求较高.第(3)小题实行了评分标准的开放性,极大地鼓舞了学生去勇于探索,不断创新.
本试题的条件和结论的开放,评分标准的开放,体现了课程标准的基本理念:“不同的人在数学上得到不同的发展.”实现了“课标”所提出的评价理念:“评价的手段和形式应多样化”,要充分“发挥评价的激励作用”,鼓励学生进行探索,产生更具创意的结果,让学生有更多的发展.
解答:(1)从条件①、②、③、④、⑤中选取3个作题设,另外2个作结论,构成一个真命题,经尝试、探索可得:如果①②③,那么④⑤.
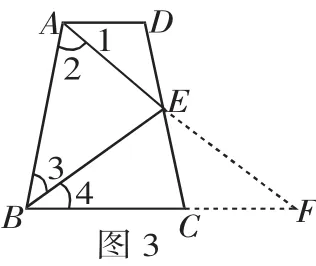
证明:如图3,延长AE交BC的延长线于F.
因AD∥BC,故∠1=∠F.
又∠AED=∠CEF,DE=CE,所以△ADE≌△FCE,AD=CF,AE=EF.
因∠1=∠F,∠1=∠2,故∠2=∠F,AB=BF.
因AB=BC+CF=BC+AD,即⑤成立.
故AE=FE,∠2=∠F,AB=BF,所以△ABE≌△FBE.
故∠3=∠4,即④成立.
(2)如果①②④,那么③⑤;如果①③④,那么②⑤;如果①③⑤,那么②④.
(3)本小题答案不唯一,写出的命题为真命题的还有:如果①②⑤,那么③④;如果②④⑤,那么①③等.
例3 如图4,下面四个条件中,请你以其中两个为已知条件,第三个为结论,推出一个正确命题.(只需写出一种情况)
①AE=AD,②AB=AC,③OB=OC,④∠B=∠C.
评析:本题是以学生常见的基本图形为载体,把传统的几何证明题,设计成一个要求学生发现、猜想、证明的组合开放题,让学生通过观察——发现的思维过程,自主探索,发现有意义的结论,积极创设思考空间,增强了学生的创新意识,养成了学生“观察——猜想——验证”正确的科学态度.
解答:本题的答案不唯一,正确的命题有:①②⇒③;①②⇒④;①④⇒②;①④⇒③;③④⇒①;③④⇒②;②④⇒①;②④⇒③共8个命题,从中任选一个证明即可.例如,证明命题①②⇒④.


“不同的人在数学上得到不同的发展”,组合型开放题因能充分体现这一新课程理念而成为最近几年中考命题的一道亮丽的风景线.它改变了过去直接给出结论,让考生去证明的固定的模式,激活了考生的思维.它启迪了我们:数学学习不仅要学习知识和方法,更要勤于思考,多探究,关注“过程”,从而体验创造的乐趣,做学习的主人.
