巧解抛物线变换问题

☉江西会昌实验学校 李 扬

巧解抛物线变换问题

☉江西会昌实验学校 李 扬

一、抛物线的平移变换

例1 （2011·重庆市江津区）将抛物线：y=x2-2x向上平移3个单位，再向右平移4个单位得到的抛物线是__________.

巧解方法：直接在一般式的自变量和因变量上分别进行“左加右减”和“上加下减”.

解：用x-4代替解析式中的x，并对其中的y（即原等式右边）加上3，就得到解析式：y=（x-4）2-2（x-4）+3，展开并整理得y=x2-10x+27.

故答案为：y=x2-10x+27.

点评：本题主要考查的是函数图像的平移，用平移规律“左加右减，上加下减”直接代入函数解析式求得平移后的函数解析式.

二、抛物线的翻折与旋转变换

（1）请直接写出抛物线c2的表达式.

（2）现将抛物线c1向左平移m个单位长度，平移后得到的新抛物线的顶点为M，与x轴的交点从左到右依次为A，B；将抛物线c2向右也平移m个单位长度，平移后得到的新抛物线的顶点为N，与x轴交点从左到右依次为D，E.①当B，D是线段AE的三等分点时，求m的值；②在平移过程中，是否存在以点A，N，E，M为顶点的四边形是矩形的情形？若存在，请求出此时m的值；若不存在，请说明理由.

方法：抛物线y=ax2+bx+c若沿x轴翻折，所得图像的函数解析式只需将原函数解析式中的y换成-y，即y=-ax2-bx-c；若沿y轴翻折，所得图像的函数解析式只需将原函数解析式中的x换成-x，即y=ax2-bx+c.

分析：（1）根据抛物线翻折的性质可求抛物线c2的表达式.

1时，当AB=AE时两种情况讨论求解；②存在.理由：连接AN，NE，EM，MA.根据矩形的判定即可得出.

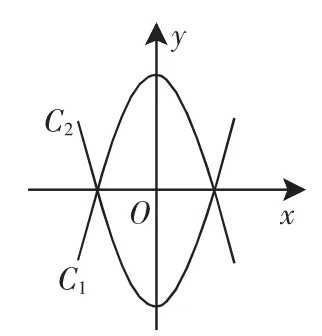
图1

图2

图3

②存在.

所以四边形ANEM为平行四边形.

要使平行四边形ANEM为矩形，必需满足OM=OA，

所以当m=1时，以点A，N，E，M为顶点的四边形是矩形.

点评：本题是二次函数的综合题型，考查了抛物线翻折和平移的性质，平行四边形和矩形的判定，注意分析题意分情况讨论结果.

例3 求抛物线y=x2+2x+3经过下列变换后的抛物线的解析式：（1）绕其顶点旋转180°；（2）绕坐标原点旋转180°.

方法：抛物线y=ax2+bx+c绕顶点旋转180°，先将一般式化成顶点式y=a（x-h）2+k，再根据变换前后开口方向改变和顶点不变，即y=-a（x-h）2+k，最后整理成一般式；抛物线y=ax2+bx+c绕原点旋转180°（关于原点对称），所得图像的函数解析式只需将原函数解析式中x换成-x，y换成-y即可，即y=-ax2+bx-c.

解：（1）把一般式化为顶点式y=（x+1）2+2.注意到变换后的抛物线仅是开口方向发生了变化，而形状、大小和顶点均未变.故所求的解析式为y=-（x+1）2+2，即y=-x2-2x+1.

（2）因为旋转前后的两条抛物线关于原点对称，所以用-x、-y分别代替函数y=x2+2x+3中的x、y即得所求解析式为y=-x2+2x-3.

点评：本题考查了抛物线旋转前后函数图像的性质，要求掌握旋转前后图像的特征与解析式中字母系数的关系.