用最低费用加快法求解成本—工期优化
2012-08-24薛俊锋
薛俊锋
(邯郸市邯三建筑工程有限公司,河北 邯郸 056001)
1 问题的提出
网络计划的优化,是通过不断调整和改善,使之达到成本最低、工期最短的过程。在一般项目施工中要加快某项工作,通常都需要增加劳动力、材料供应、机械设备等,而这些增加均会引起成本的增加,因此工程成本与工期有着密切的关系。对某一个项目而言,既不能简单地认为缩短工期就会增加成本,也不能认为延长工期就会降低成本,所在地就存在一个时间与费用的优化问题,即网络计划工期与成本的优化。
2 工期-成本的关系
(1)工期—成本的关系曲线。工期成本时由直接费用和间接费用组成的,一般情况下,压缩工期将引起直接费用的增加和间接费用的减小;反之,延长工期会使直接费用减小,直接费用增加。
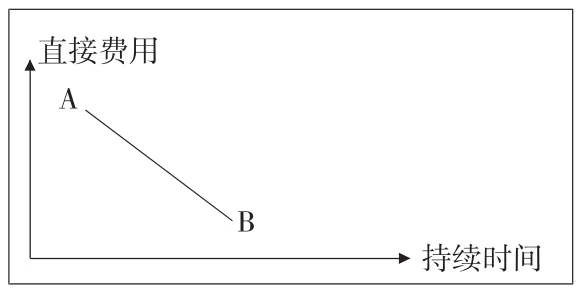
图1 工作持续时间与直接费用曲线
(2)费用率。为简化起见,通常可用直线AB表示工作持续时间与直接费用的关系(如图1)。任意一项工作的费用率ei-j,反映该工作缩短(或延长)单位持续时间所需增加(或减少)的费用数额,即ei-j=(mi-j-Mi-j)/(Di-j-di-j)其中,Mi-j和mi-j表示持续时间变化前后的直接费用,Di-j表示压缩前的持续时间,di-j表示缩短后的持续时间。
3 优化方法
工期成本优化是以工程成本最低为前提寻求工期最优的优化方法。其基本方法是,从网络计划的各工作持续时间和费用关系中,依次找出一方面既能使工期缩短,另一方面又能使得费用增加最少的工作,不断地压缩其持续时间,同时考虑间接费的增加,即可求出工程成本最低时的相应最优工期。关键路线的持续时间决定工期的长短,因此压缩工期首先应缩短关键路线的持续时间,而且,首先应压缩费用率最小的关键工作的持续时间,即“最低费用加快方法”。
4 实例分析
某工程双代号网络计划如图2所示,图中箭线下方括号外数字为工作的正常时间,括号内数字为最短持续时间;TF为某工作总时差。间接费率为1.45万元/天。各工作的工期一成本数据列于表1中,计算后所得的费用率e也列于表1中。现对其进行费用优化。
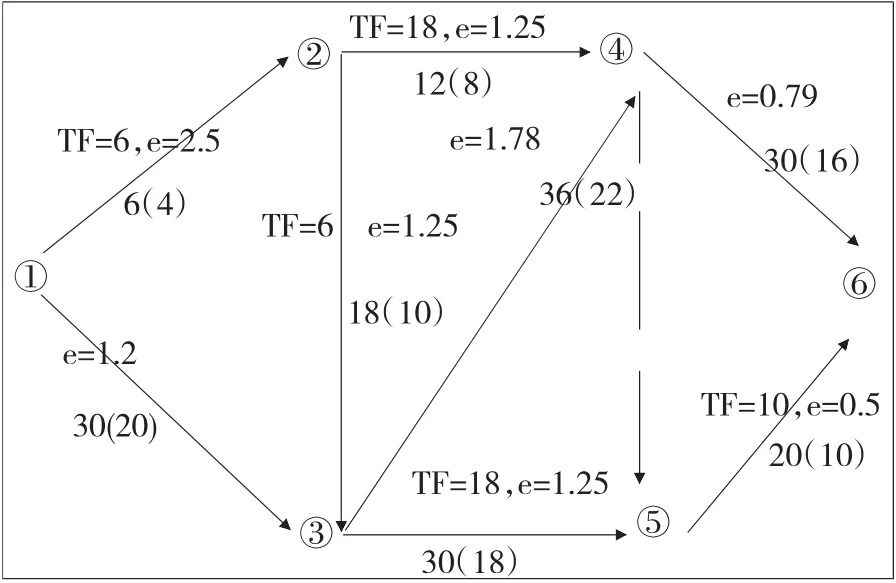
图2 某网络计划图
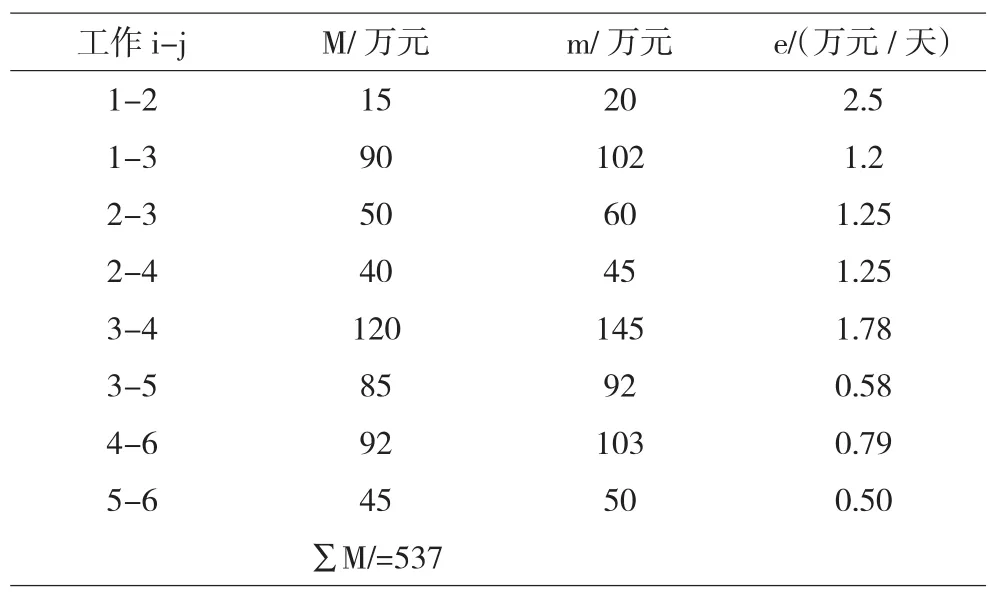
表1 各工作的工期成本数据表
网络计划费用优化可按以下步骤进行:
(1)第一次压缩:从图3可知,该网络计划中关键线路为①→③→④→⑥,费用率最小的关键工作为④→⑥,e4-6=0.79。工作④→⑥的持续时间可压缩30-16=14天,但是由于工作⑤→⑥的总时差只有10天,所以△t1=min<14,10>=10天
则△S1=e4-6*△t1=0.79*10=7.90 万元,S1=△S1+S0=537+7.90=544.90万元。
第一次压缩后,图2变为图3
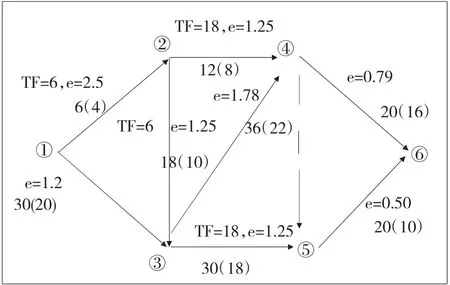
图3 第一次压缩后的网络计划图
(2)第二次压缩:在图3中,有两条关键路线,分别为①→③→④→⑥和①→③→④→⑤→⑥。第一条线路上e最小值e4-6=0.79,第二条线路上e最小值e5-6=0.50,则∑e=0.79+0.50=1.29,所以宜压缩工作①→③。工作①→③的持续时间可压缩30-20=10天,但工作②→③的总时差为6天,因此工作①→③的压缩时间为△t2=6天。则△S2=e1-3*△t2=1.20*6=7.20万元,S1=△S1+S0=544.90+7.20=552.10万元
(3)第三次压缩:第二次压缩后,网络图更新为图4,在该图中关键线路有4条,能缩短工期的切割方案有4种,即:
AA切割,∑e=1.2+2.5=3.7
BB切割,∑e=1.25+1.2=3.75
CC切割,∑e=1.78
DD切割,∑e=0.79+0.5=1.29
因此,选择e最小的方案,即DD方案。
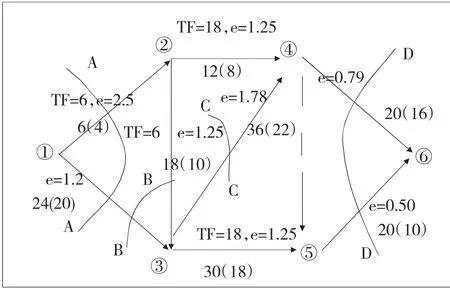
图4 第二次压缩后的网络计划图
工作④→⑥可缩短4天,工作⑤→⑥可缩短10天,所以t3=min<4,10>=4天
△S3=∑e*△t3=1.29*4=5.16万元,S3=S3+S0=552.10+5.16=558.26万元
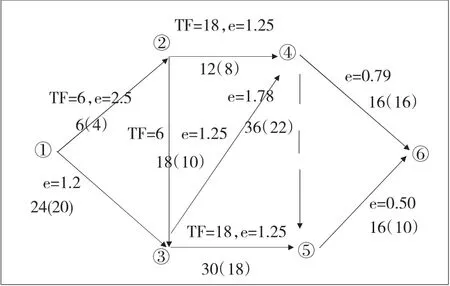
图5 第三次压缩后的网络计划图
经过三次压缩,原网络图最终变为如图5所示,工期变为76天。
将上述优化过程中的结果及相应的间接费汇于表2中,可知最优工期为80天,工程成本为668.1万元。
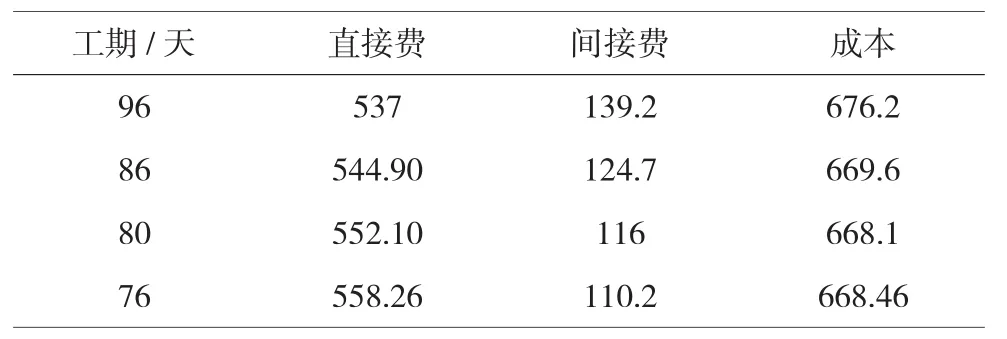
表2 优化后的工期成本数据表
5 结语
我们可以看到,工期成本优化主要是通过系统择优压缩原理,利用费用率从总体上进行同步压缩,不断压缩工程的直接费率,从而寻求满足要求的最优方案的过程。为缩短工程建设时间、控制工程成本提供了有效解决办法。
