高三数学复习课教学方法探究

2012-08-24黄慧琴

镇江高专学报 2012年4期

黄慧琴

(江苏省镇江第一中学，江苏镇江 212016)

基于目前的高考模式，高三的数学复习尤其重要。在复习过程中，教师采用何种教学方法培养学生的数学能力，使其积极应对高考至关重要。

1 遵循“建构主义”原理，淡化概念，强调意义

建构主义认为，认识不是人脑对事物直接的、简单的反映，而是以原有知识为基础，在主客体的相互作用中建构而成的，学习实质上是一种“意义建构”［1］。学习不是简单的信息积累和死记硬背，而是新旧知识经验的冲突以及由此引发的认知结构的重组。学生不是被动接受知识，而应是主动建构知识。学生不会对掌握一章一节的知识感到困难，但应对综合问题时往往感觉力不从心。教师不妨遵循建构主义原理组织教学，并变换角色，从传统的传授知识者，转变为学生学习的辅导者、合作者［2］。

基于建构主义的教学，避免了传统教学中只强调教学的统一性、规范性、模仿继承性，以不变应万变地消极适应高考的缺陷，避免了教师的满堂灌，为学生创造了更多提高和展示自己的机会，最大限度地开发了学生的潜能和特长。基于建构主义的教学，对教师而言，事先的准备工作、课堂的组织工作大大增加了，不仅要提出有质量的学习任务，让学生去思考、讨论、发现、联系，建构自己熟悉和易懂的数学模型，还要让学生多提几个为什么，弄清相应数学概念和基本知识，理顺它们之间的关系，以掌握知识、提高能力、发展个性。如“错位相消法”的原型出现在数列an=a1qn－1(a1≠0，q≠1)的求和中。学习等比数列时，以“求2+22+23+…+2n－1的和”为例，引导学生思考如何消项。有的学生仿照等差数列求和问题进行配对，但发现不管是前后配对还是首尾相加都不能形成合适的结构。此时，教师加以引导“相加不行，作差呢?”“一个等式无法作差，能否尝试用两个等式作差?如果可以，如何做呢?”学生在探索

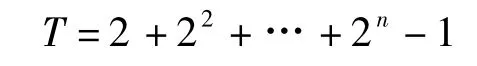
变形中找出规律:

与原式类似，而且出现了n－2个相同项，作差得

趁热打铁，计算

学生主动进行类比，总结规律:将等式两边同乘以公比q后作差得

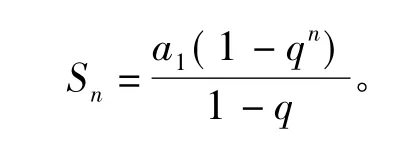
在教师的引导下进行意义建构，有事半功倍之效。

2 辅以数学思想方法，提高数学思维能力

到了高三，学生除了要理解基本概念外，还要会解题，即在较短的时间内判断出题目所考查的知识点，及时选择正确的解题方法。教师在讲例题时要注重解题方法的指导。数学思想方法是数学知识在更高层次上的抽象和概括，它蕴涵在数学知识发生、发展和应用的过程中，分析问题既要“由因导果”，也要“执果索因”［3］。首先，教师对例题的选择要做到精、新、多变。其次，注重对知识点的整理、分类、综合，以点带面，形成完整的知识体系，避免重复做题。再次，引导学生积极探索、总结、反思，选择最佳学习策略。教师讲解例题时，要充分展示自己的思路、解决问题的切入点，让学生把握数学知识之间的内在联系，培养分析问题和解决问题的能力。如果不暴露思维过程而直接给出答案，学生不仅记忆不牢固，理解也会浮于表面，做题时往往只会机械模仿，不会深入思考，更不会变通。

3 营造轻松、愉快的学习环境

轻松、愉快的心情会激发大脑皮层的神经单元形成兴奋中心，促进思维，增强知识接受能力，而在紧张的状态下，大脑皮层的神经单元会受到限制。高三学生学习任务重、压力大，教师要注意营造轻松、愉快的学习氛围，让学生充分发挥自己的聪明才智和想象力，提高学习效率。以平等、宽容、友善、欣赏的态度对待学生，热情鼓励的目光、一次表现机会都可能给予学生无形的力量、钻研的动力［4］。多关心学生的学习和生活，给予其个性发展的环境和空间，让他们切切实实体会到你的关爱，愿意敞开心扉和你交流。根据学生身心发展的特点和知识发展水平，拟定习题的难度，让学生尝到成功的喜悦。教师还要让学生在克服困难中锻炼意志，找回自信，增强心理承受能力，提高心理素质。

4 做有心人，聚焦知识盲点

复习时，学生往往会出现这样的情况:同样的题目，间隔一段时间，还会发生同样的错误。笔者除了建议学生记下错题，记下错误的思路，找出产生错误的原因，形成正确的解题方法，还让学生学会建模，掌握类比、归纳、构造、数形结合等数学思想方法。数学学习不能停留在简单的计算和死记硬背上，要善于动脑，注意问题的转换，养成良好的学习习惯，培养创新能力［5］。教师在上课时，可故意设置障碍，让学生在合作中发现思路，在对比中掌握知识，使思维上升到新的高度［6］。