一维谐振子的数值方法研究①

陈海军

(陇东学院物理系，甘肃庆阳745000)

0 引言

谐振子问题是量子力学和经典力学中的基本问题.任何体系在平衡位置附近的振动，例如，分子的振动，晶格的振动，原子核表面振动以及辐射场的振动等等，在适当的坐标变换之后，都可以分解为若干彼此独立的谐振动.谐振动还可以作为任何复杂振动的初步近似.在量子力学中，谐振子问题的精确求解过程，不仅提供了一整套量子力学处理具体问题的方法，而且为处理其它量子力学问题提供了物理基础.

鉴于大多数量子力学教科书都提供了一维谐振子问题的解析求解过程，本文简述一维谐振子问题的理论求解过程，然后利用数值计算的方法求解其定态解，并研究其随时间的演化规律.这种数值求解过程是数值方法研究其它量子问题的基础.

1 谐振子问题理论求解

根据量子力学教科书［1］简述一维谐振子问题的理论求解过程.

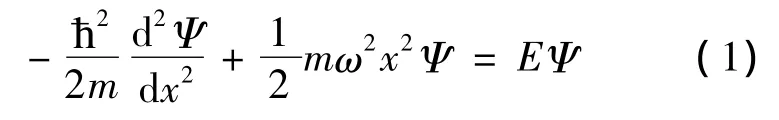
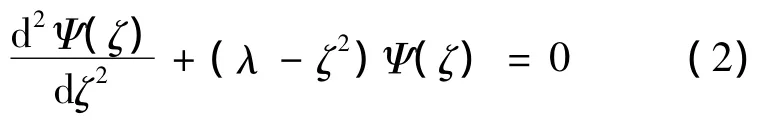
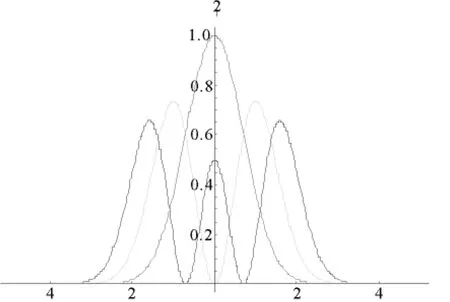
图1 解析解波函数及波函数的模方

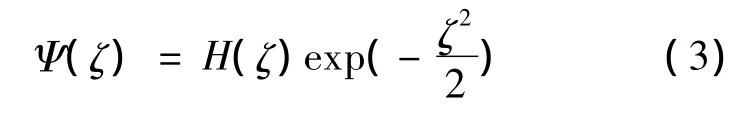
代入方程(2)得到

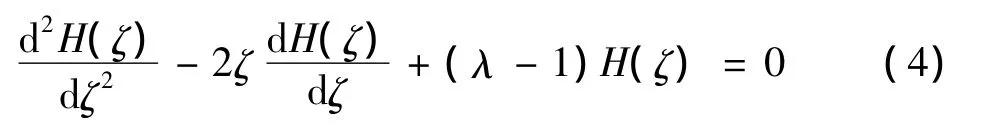
级数展开求解，令

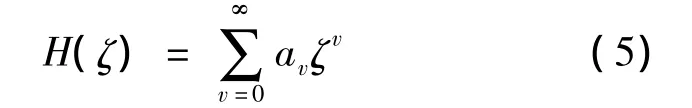
代入方程(4)得到递推公式

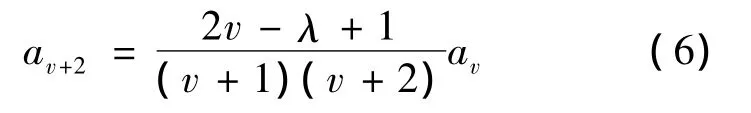
方程(6)表明级数H(ζ)和exp(ζ2)具有相同的收敛性，是发散的，因此必须取有限项使得H(ζ)变为厄米多项式Hn(ζ)，则有

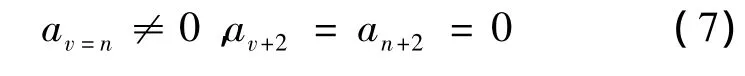
得到λ =2n+1，则能量

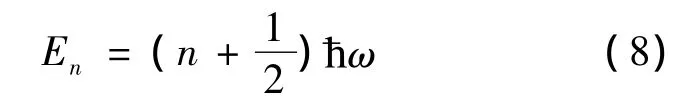
因此和En相应的归一化波函数是

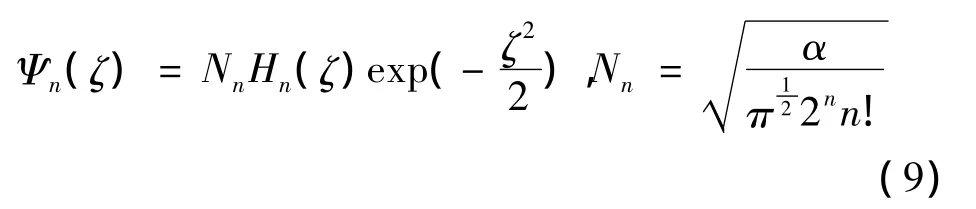
其中Nn为归一化系数.

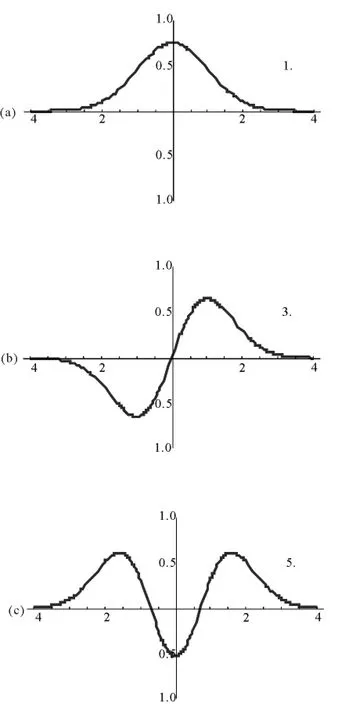
图2 数值计算得到前三个能级所对应的波函数

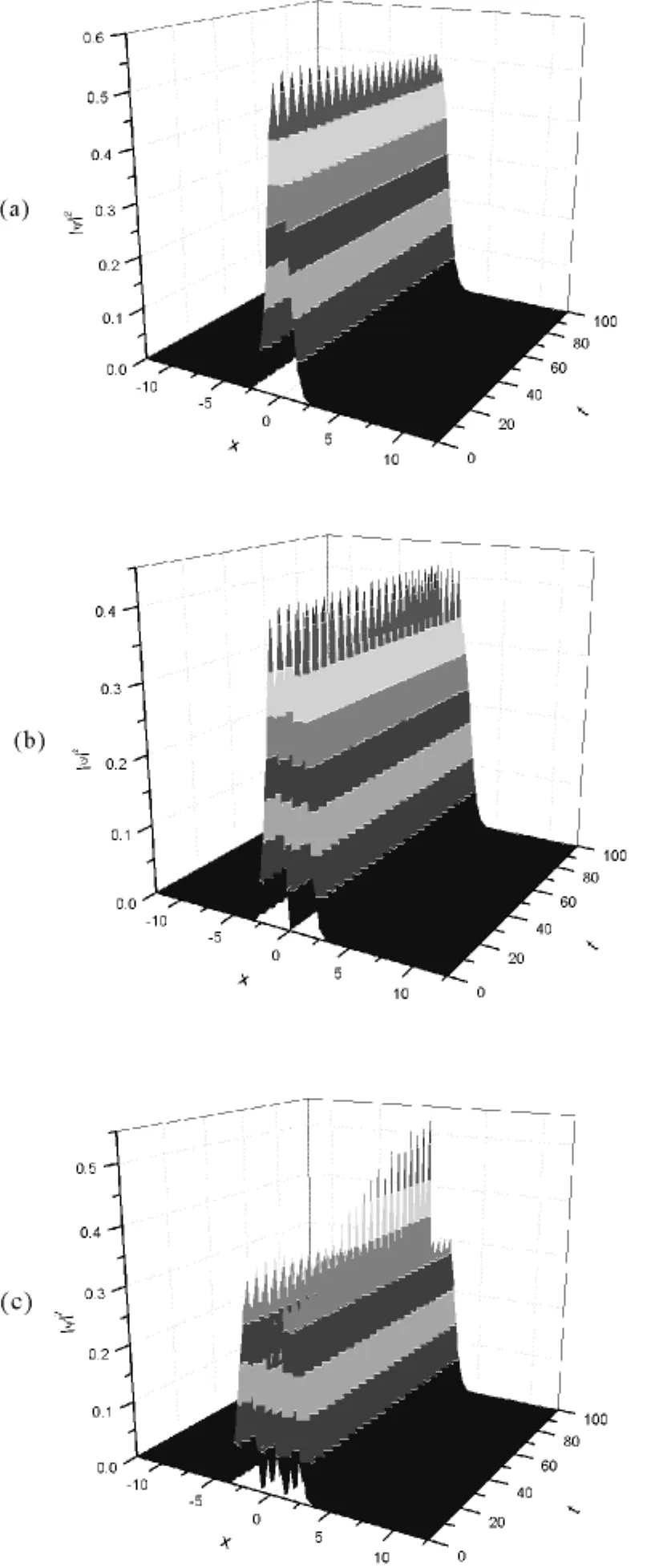
图3 定态随时间传播过程

表1 前三个状态的能量及波函数

表1给出前三个状态的能量及其波函数.图1给出前三个解析解对应的波函数模方，即粒子出现概率密度的空间分布.可以看出处于基态和第二激发态(n=0，n=2)的粒子在势阱中心有一定概率出现，其中，处于基态的粒子在势阱中心出现的概率最大，而处于第一激发态的粒子在势阱中心出现的概率为0.

2 定态问题数值计算

量子力学中的大多数问题不可能求出解析解，因此利用数值计算方法研究谐振子问题具有重要意义.该方法不仅可以求解谐振子问题本身，而且可以扩展到其它的量子问题上，只要把其中的势能函数替换为想要求解体系的势能函数即可.束缚定态问题的数值求解，在数值计算方法中归结为偏微分方程的边值问题求解.这类问题求解多采用打靶法，即取微分方程中某一个参数作为数值计算的试探参数，利用计算机快速计算的能力，在参数取值的物理区间内，按一定的步长改变参数值，直到得出的数值结果满足物理问题要求的边界条件即可.

本文利用Mathematica软件中的NDSolve命令求解方程(2)的边值问题［2］.自变量的变化范围是－∞ ＜ζ＜∞，在数值计算时取 －4≤ζ≤4.由于求解的是束缚定态问题，因此波函数Ψ(ζ)在边界上的取值应为0，数值计算时，采用|Ψ(±4)|＜10－3.另外，由于势能 V(ζ)具有对称性，所以体系具有明确的宇称，在计算过程中偶宇称解和奇宇称解的求解分别进行.在计算过程中，取λ为试探参数，从0开始循环，步长为0.001，直到定态结果出现为止.

计算结果如图2所示，图2(a)和(c)表示偶宇称波函数(n=0，2)，图2(b)表示奇宇称波函数(n=1).数值计算结果给出 λ =1，3，5，对应的能量是 E= ħω/2，3ħω/2，5ħω/2，和理论结果一致.

3 定态稳定性研究

为了验证定态解的稳定性，我们利用Crank－Nicholson差分法求解含时Schrdinger方程［3，4］，时间步长τ和空间步长h分别为0.001和0.1，x方向的网格数为250.把表1中的定态解作为求解含时Schrdinger方程的初始条件，研究其随时间变化的规律.

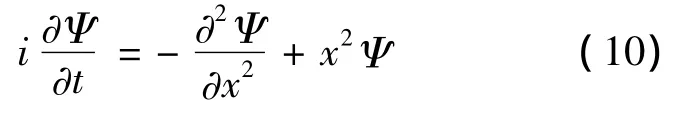
其中时间无量纲化单位是2/ω.差分格式是

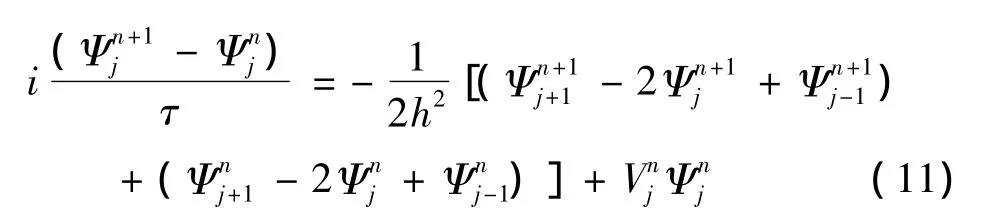
其中V=x2是势能函数.

图3表示n=0，1，2所对应定态|Ψ|2随时间的传播过程，即粒子出现概率空间分布随时间变化过程.图(a)表示基态概率分布随时间的传播过程，其实质是高斯波包在抛物型势阱中的传播过程，如果没有势阱的作用，波包由于色散作用，随时间传播会扩散，而由于势阱的束缚作用，高斯波包在传播过程中保持初始时刻的波形，是稳定的传播过程.第一激发态的传播过程也是稳定的(图(b)).图(c)表示第二激发态随时间的传播过程，和前两个状态的传播过程不同，在传播时，两边的概率会向势阱的中心移动，但是并没有坍缩.另外，整个传播过程是呼吸振荡的.

4 结论

本文利用数值计算方法研究了量子力学中一维谐振子问题.包括定态和含时过程的求解，定态计算结果给出了能量和定态所对应的波函数，和理论分析结果一致.含时过程计算表明处于定态中的粒子出现概率空间分布是不随时间变化的，这是定态的基本性质之一.整个求解过程中涉及到定态问题和含时问题的数值计算，这两类问题的数值计算是研究量子问题的基础，尤其体系稳定性问题，由于能进行理论分析的体系很少，所以只能依靠数值求解含时薛定谔方程来研究.因此本文介绍的方法可以推广到其它量子体系的研究，甚至包括非线性薛定谔方程所描述的体系.

［1］苏汝铿.量子力学(第二版)［M］.北京:高等教育出版社，2002.

［2］董键.Mathematica与大学物理计算［M］.北京:清华大学出版社，2010.

［3］彭芳麟.计算物理基础［M］.北京:高等教育出版社，2010.

［4］Sadhan K Adhikari，Paulsamy Muruganandam.Bose － Einstein Condensation Dynamics from the Numerical Solution of the Gross－ Pitaevskii Equation［J］.J.Phys.B:At.Mol.Opt.Phys.，2002，35:2831 －2843.