三维移测架流固耦合动力学分析①
2012-08-21王懿晨杨志刚李启良
王懿晨, 杨志刚, 李启良
(同济大学上海地面交通工具风洞中心,上海201804)
0 引言
风洞实验可以测量物体引起的所在空间各点物理量分布,但是测量仪器的介入必然导致流场的改变,从而影响测量结果的准确性.正如用于空间测点定位的三维移测架,当实验风速较高时,流场压强变化剧烈,气动力足以导致移测架结构发生扭转与弯曲振动,从而影响实验测量精度.过去对于移测架的研究主要集中在其控制系统上[1-2].关于移测架本身对流场干扰的影响的研究很少.正因如此,本文在过去研究基础上[3],关注移测架自身的振动与流场特性,通过对流场和结构振动的分析,获得流动对测量的影响,为进一步改进结构做好准备.
1 计算方法
由于结构变形量仅有毫米数量级.本文忽略弹性结构对流场的影响,采用结构弹性运动的单向流固耦合仿真方法,即CFD计算结果单向的传递给固体结构分析.
1.1 计算模型
图1所示为三维移测架模型.由于测点定位滑块的大小与质量相对于整个梁结构较小,对于结构振动的影响也较小,因此本文研究忽略滑块.
1.2 流场计算方法
计算域选取图2所示的区域,即L×W×H=1800mm×7500mm×2700mm.边界层贴附在移测架表面,第一层厚度0.5mm,增长率为1.2,共计五层.体网格采用四面体、五面体和六面体网格的混合型网格.最终流体网格数量570万.
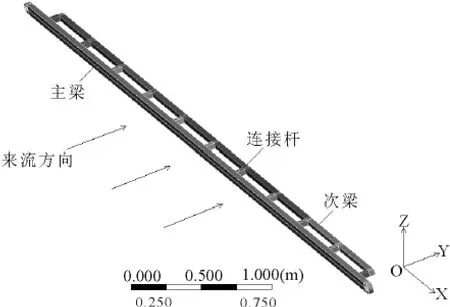
图1 三维移测架模型
采用大涡模拟(LES)方法以捕捉湍流的瞬态特性.非定常迭代时间步大小设置为0.0005秒.首先采用Realizable模型,获得稳定解后,使用LES计算1s后,进入动态稳定阶段后,将结果与结构分析相结合.
1.3 结构分析方法
根据移测架表面几何形状,生成40万个结构体网格.通常风洞实验,移测架需要等流场动态稳定后才使用.因此本文不考虑流场建立过程中的结构响应,只考虑流场动态稳定后,结构的振动情况.
为了实现流固耦合分析,本文采用ANSYS瞬态求解模块与FLUENT流场求解模块联立求解计及梁结构弹性的结果.在施加非定常流场之前先叠加一个稳定的定常流场,使得梁结构产生一定的预变形.等结构的瞬态响应衰减之后,撤去定常载荷,同时加载非定常流场计算结果,获得弹性结构的动态响应.
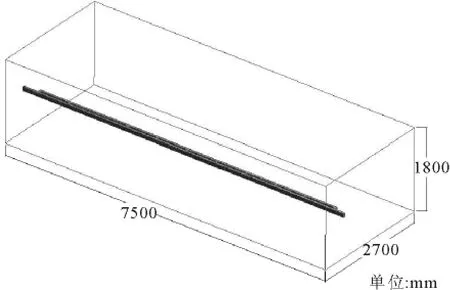
图2 计算域
2 计算结果与分析
2.1 流场分析
结构振动的激振力来自流场的气动力,通过LES计算可以得到表1所示涡脱落的频率.该频率主要是大尺度漩涡的脱落频率.
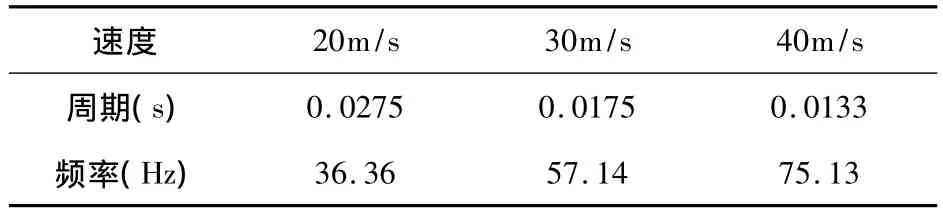
表1 不同流速下,涡脱落频率
为了更加清晰地辨识是否存在其它激振频率.在移测架尾部布置12个测点,测点的布置如图3所示.
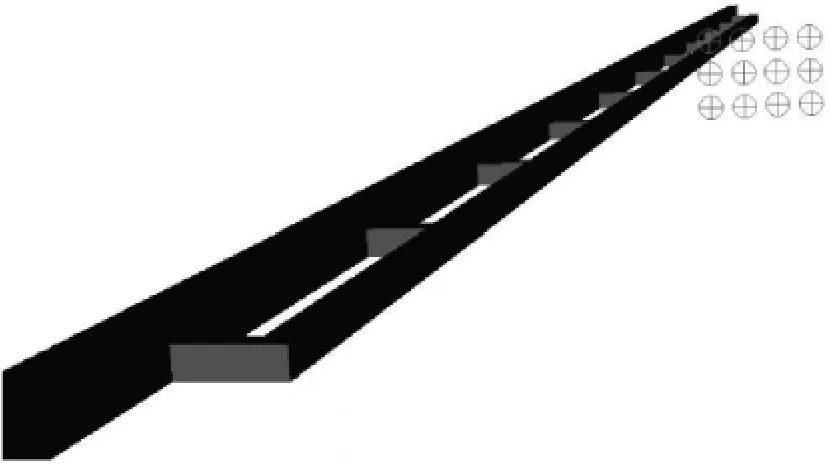
图3 速度测点布置
对监测点速度的进行快速傅里叶变换的结果,如图4所示.
尾部速度频谱除显示出大尺度漩涡的脱落频率外,还获得另一个更高的频率.该频率值是大尺度涡脱落频率的两倍.这一频率是由诱导涡造成的.正如图 5 所示的 30m/s流速下,1.3900s,1.3925s,1.3950s,1.3975s 时刻横截面的涡量云图.1.3850s时刻,上游主梁脱落一个涡,同时尾迹距离减小.这一脱落涡在次梁的上沿诱导出一个反向涡,在脱落涡向下游移动的过程中,反向涡逐渐增大并脱落.在1.3950s时,主梁的边界层尾迹重新增长到次梁的上沿,但并未脱落,而是持续的从边界层中获得能量,因此在1.3975s时,脱落的反向涡很快消失.正是这样一个反向诱导涡的产生、脱落和消亡的过程产生了频率谱中的高阶峰值.
2.2 模态分析
在模态分析中,根据移测架所使用的材料与实际实验流体(空气),确定表2所示的物性参数.
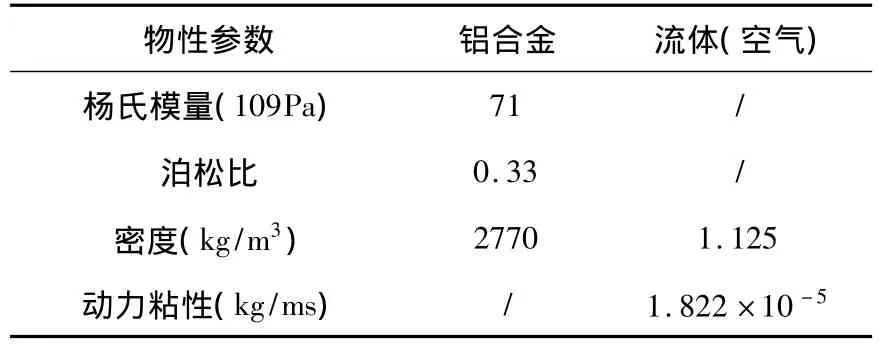
表2 物性参数
出于滑块安装和移动的需要,移测架迎风侧的横梁横截面被加工成矩形,这势必导致梁结构的刚度降低.因此,为了增加结构刚度,风洞移测架在迎风侧的矩形梁之后额外增加一根起加强作用的辅助梁,以期增加梁结构在迎风方向上的抗弯刚度.两根横向梁通过长度为90mm的纵向连接杆连接.可以预测在连接杆连接处梁的整体刚度有所加强,在振型中的反映便是连接处的曲率要低于其他区域,这也导致梁结构在实际振动中不易出现高阶振型.出于垂向移动的目的,实际风洞使用的移测架两端采用铰链支承形式以安装滑轮,本文计算中采用实际安装形式,铰支承轴向与来流方向相平行.
通过计算获得移测架结构的前10阶模态如表3所示.
由于梁结构的横截面呈矩形,因此可以预见梁的各阶振型应该是随模态阶数增加而在流动方向与垂直流动方向上交替产生最大振幅.对于所关注的低频模态区域,由于采用铰支承形式,相邻的两阶模态的频率往往非常接近,但是最大位移却分别发生在垂直方向和流动方向.2阶与3阶、4阶与5阶、6阶与7阶的频率相当接近,因此当激振力频率位于10Hz、25Hz和45Hz附近时,将极有可能使得梁结构在流动和垂直方向上都产生共振,从而使得振动加剧.
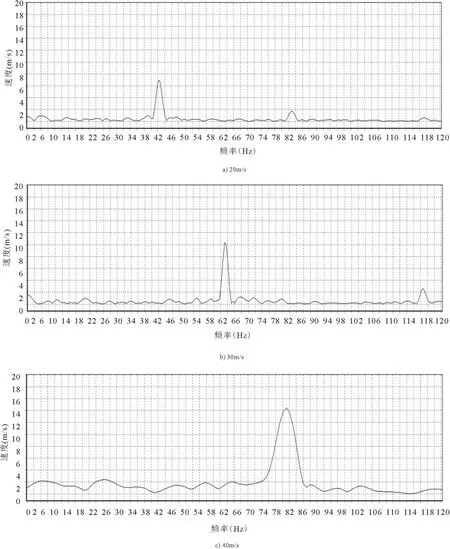
图4 不同来流速度下,速度脉动的频谱
图4 显示了移测架结构的第一、第二阶固有振型.两阶模态的流动方向和垂直方向振幅的比值分别为0.131和8.479.可见,当发生共振时,将会产生某一方向位移占主导的振型,占主导的方向上位移可以达到另一方向位移的8倍.
2.3 流固耦合分析
通过求解绕移测架的非定常流场的N-S方程,获得绕流的流场以及移测架表面的气动压强.然后通过插值方式将流体域压强传递给结构域,再以此作为激振力施加于结构,进行动力学计算.耦合计算结果如表3所示.从表3可以看出,梁变形位移主要是由时均气动力造成的,变形量在40m/s流速下可以达到将近3cm,而压力脉动所造成的振幅只能达到1.65mm.变形与振幅均不随来流速度线性增加.振幅占变形的比例随着来流速度的增加而减小,因此从测量角度考虑,定常压强的影响要大于脉动量.另一方面,垂直方向的变形量大约是水平方向的两倍,这是由于流动方向上的抗弯刚度通过添加次梁而有所加强.根据表3的流动方向和垂直方向的振幅比值分别为 0.235,0.131,0.267,可以看出在流速从20m/s上升到30m/s时,流动方向的振幅几乎没有变化,但是垂直方向上的振幅几乎增大了一倍.在30m/s的速度下,移测架结构表现出一阶振型,可能已经发生了共振.从频率角度看,30m/s来流速度下振动频率是在3.7Hz左右,这与模态分析结果(2.7Hz)不相符合,可能的原因是由于定常气动力作用于梁结构,使得梁结构产生内应力,从而使得结构的固有振动频率向较大的方向偏移.
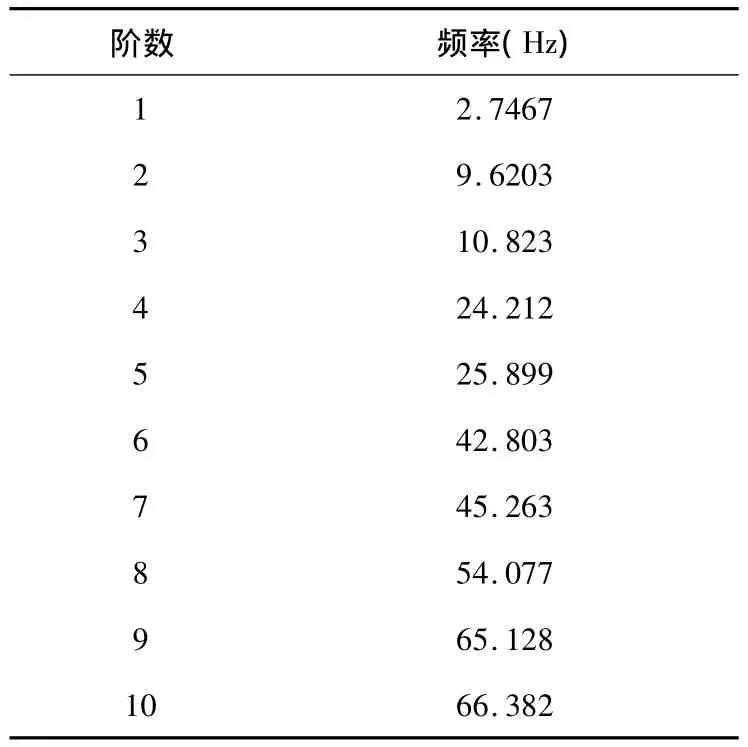
表3 移测架各阶模态
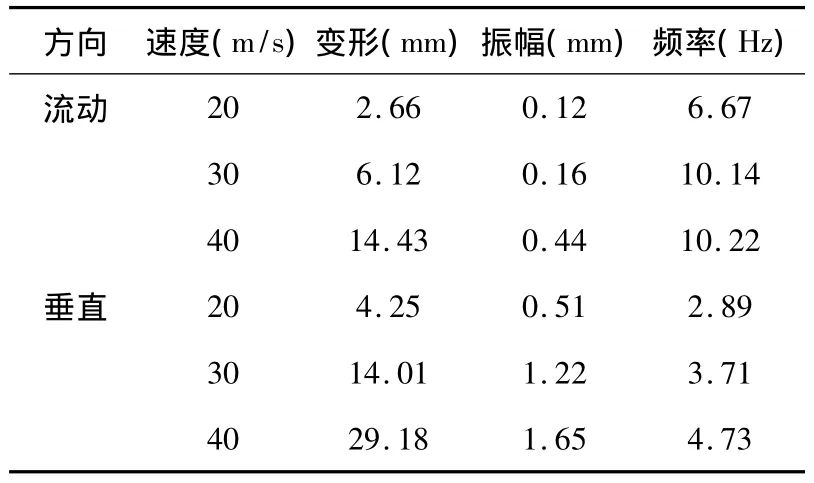
表4 流动方向与竖直方向变形量
另外,大尺度涡脱落频率大于移测架的低阶共振频率,但是由于实际发生的是湍流涡脱落,存在低频振动激励,同时移测架结构刚度通过添加次梁而得到增强,不易在梁跨度上产生驻点而形成高阶振型,因此在多种激振频率共同存在的条件下,移测架主要表现为低阶振型.
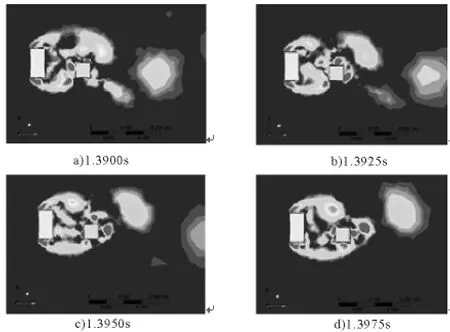
图5 不同时刻的涡量图
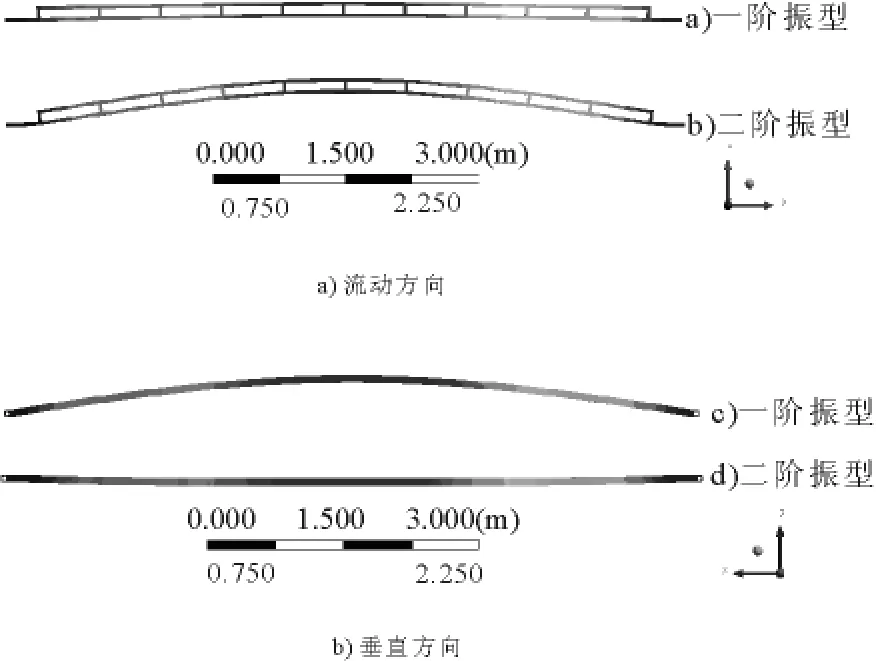
图6 移测架一、二阶振型
3 结论
移测架的变形量主要由定常载荷造成,定常载荷造成的变形量远大于脉动量造成的振幅,同时变形量随着流速的增大而呈非线性关系,随着流速的增加而快速增加.
在流速小于40m/s范围内,只出现低阶振型.随着流速的增加,导致移测架内应力增大,从而各阶模态的固有频率有所升高.
流场的大尺度涡脱落频率随着流速的增加而线性增加,但是激振频谱中,除了大尺度涡脱落频率之外,还存在诱导涡脱落的频率以及其他各频率的激励源,其中包括低阶模态频率,因此移测架的主要振型表现为低阶模态.
[1]孙泽昌,史幼迪.三维风洞移测架座标定位控制系统[J].电气传动和自动控制,1992,6:22 -25.
[2]杨立军,施洪昌.风洞移测架控制系统[J].测控技术,2005,24(4):80-81.
[3]Zhigang Yang,Qiaoyun Liu,Qiliang Li.Effectof Traversing System on Wind Tunnel Flow Field[J].Procedia Engineering,2011,12:15 -20.
[4]李增,张志谊.含弹性连接和层间流体的双梁结构的耦合振动分析[J].振动与冲击,2010(7):189 -192.
[5]Atsushi Okajima,Satoru Yasui,Takahiro Kiwata,Shigeo Kimura.Flow-induced Streamwise Oscillation of Two Circular Cylinders in Tandem Arrangement[J].International Journal of Heat and Fluid Flow,2007(28):552 -560.
