桩－沙土相互作用地震分析研究①

马东亚， 曾大明， 赵 扬

(1.同济大学结构工程与防灾研究所，上海200092;2.中国海诚工程科技有限公司，上海200031;3.上海市中森建筑与工程设计顾问有限公司，上海200120)

0 引言

桩基础具有较高的竖向承载能力和刚度，因此适用于上部竖向荷载较大且地质条件复杂的场地环境中.然而在历次地震如日本新泻地震(1964年)、美国阿拉斯加地震(1964年)和中国唐山地震(1976 年)等都看到了沙土液化现象［1，2］.图 1 是在日本新泻地震中由于沙土液化导致上部建筑物倾倒.归其原因是由于地震作用下，饱和砂土或粉土孔隙水压力上升，地基液化承载力和刚度急剧退化［3］，然而在桩基础设计中并没有很好的应对之策.

图1 日本新泻地震场地液化

分析饱和砂土中桩－土相互作用的方法很多，其中振动台试验是最直接有效的方法，然而由于费用、缩尺和适用对象的单一性，因此数值模拟可以作为较好的补充［4］.

图2 计算有限元模型

图3 三维土－水土耦合单元

现有有限元软件几乎都可以考虑计算强震时域内土的非线性，但要实现强震下砂土液化的固－液耦合问题，模拟起来比较困难.OpenSees因其内置多种可以考虑固－液耦合的本构模型，因此可以较好的模拟液化下桩－土相互作用［5］.

图4 桩－土刚性连接

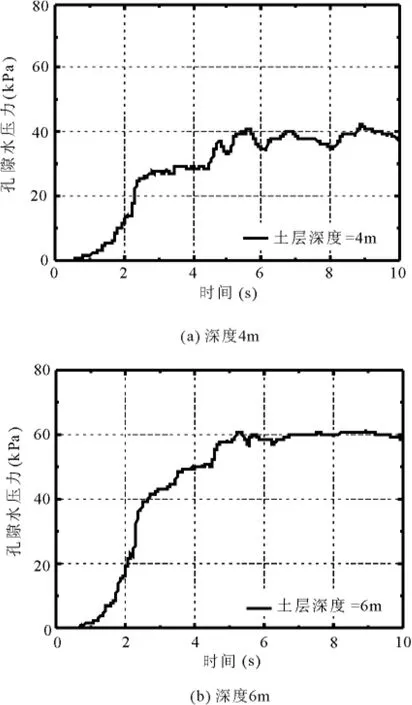
图5 孔隙水压力El Case

1 计算模型

模型中桩单元的常数以及属性见表1.土分为两种，上部2m为软粘土，下部10m为砂土，其中饱和砂土的材料属性见表2.在桩顶位置施加5吨集中质量块代替上部结构.有限元模型见图2.

表1 桩基础材料属性

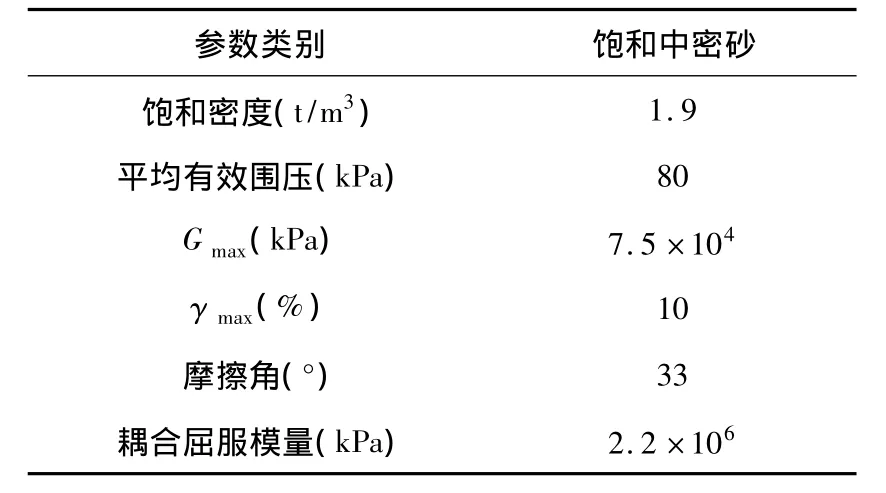
表2 沙土材料属性

图6 孔隙水压力Sin Case

在分析模型中，粘土采用多屈服面塑性本构模型，将粘土模拟为非线性滞回材料，且具有米塞氏多面运动塑性变形特征［6］.砂土采用多屈服面塑性模拟，该模型基于初始多屈服面塑性理论(Prevost模型理论框架)，采用多屈服面方法模拟砂土循环滞后反应［7］.

砂土体采用能考虑孔压消散重分布并与孔压关联的三维土—水完全耦合(u－p)8节点六面体线性等参单元模拟见图3，具体为:每一节点都有4个自由度，自由度1到自由度3表示三个方向的平移自由度(u)，自由度4表示孔压(p).基于Biot动力方程分析土颗粒与水之间的动力相互作用，并通过模拟土－水完全耦合物理过程实现该单元［8］.

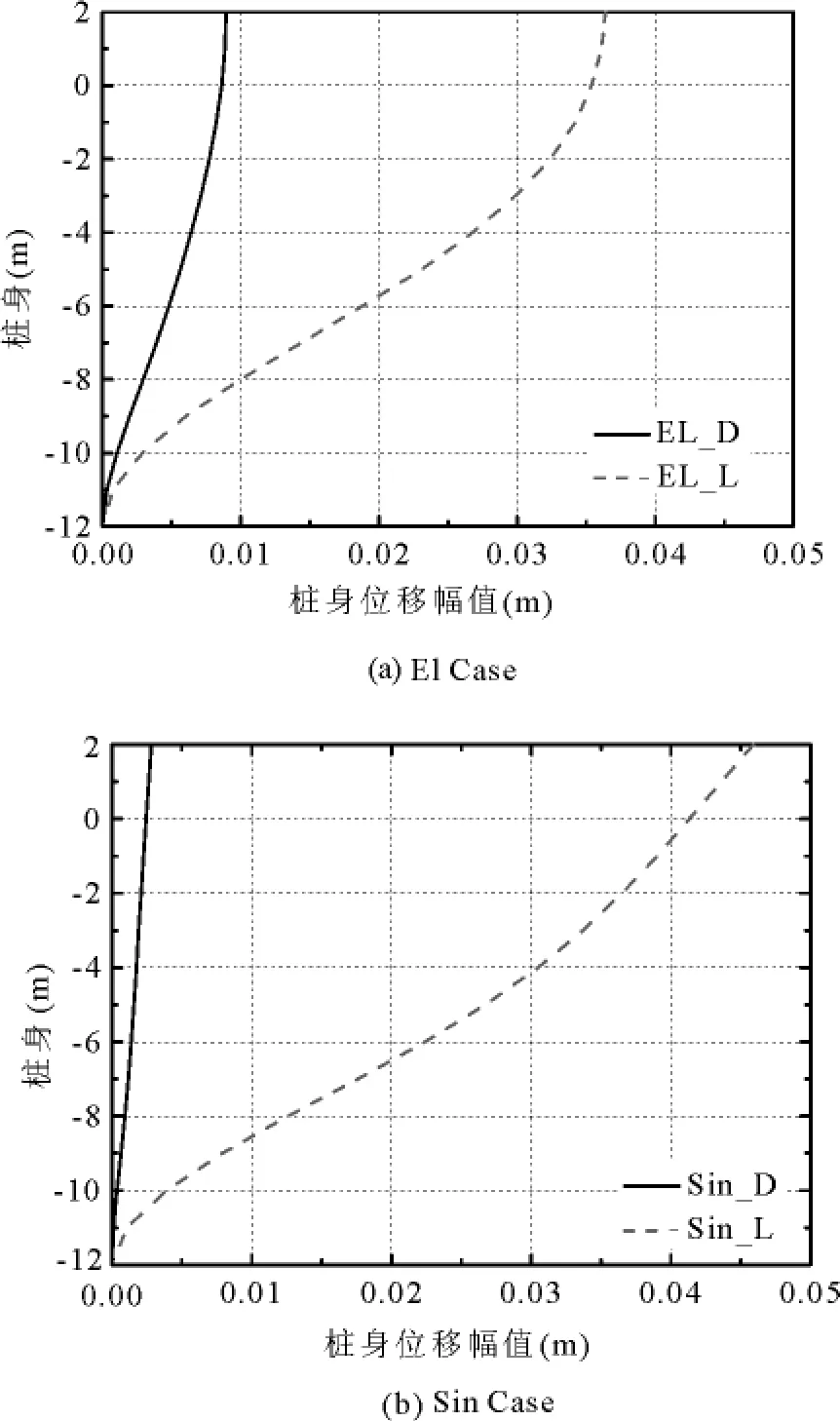
图7 桩身位移幅值

表3 加载机制

采用刚性连接单元模拟桩—土相互作用见图4，杆单元组成径向放射辐连结模拟桩的梁单元节点和桩周土单元节点，将杆单元轴向刚度取得足够大以保证杆件在桩平面截面上将荷载传给土单元，而受到弯矩作用前后桩满足平截面假定，杆单元的力只能在沿杆单元的连结方向传递.

土体底面所有节点固接;土体周边边界选用shear beam边界(将模型周边边界每一层所有节点的水平向自由度捆绑在一起)以反应振动台试验模型箱柔性容器对土体约束的剪切梁效应;基底假定为刚性基岩;约束对称面y向平移自由度.

本次计算荷载的加载机制见表3，其中El表示El Centro波，Sin表示正弦波.

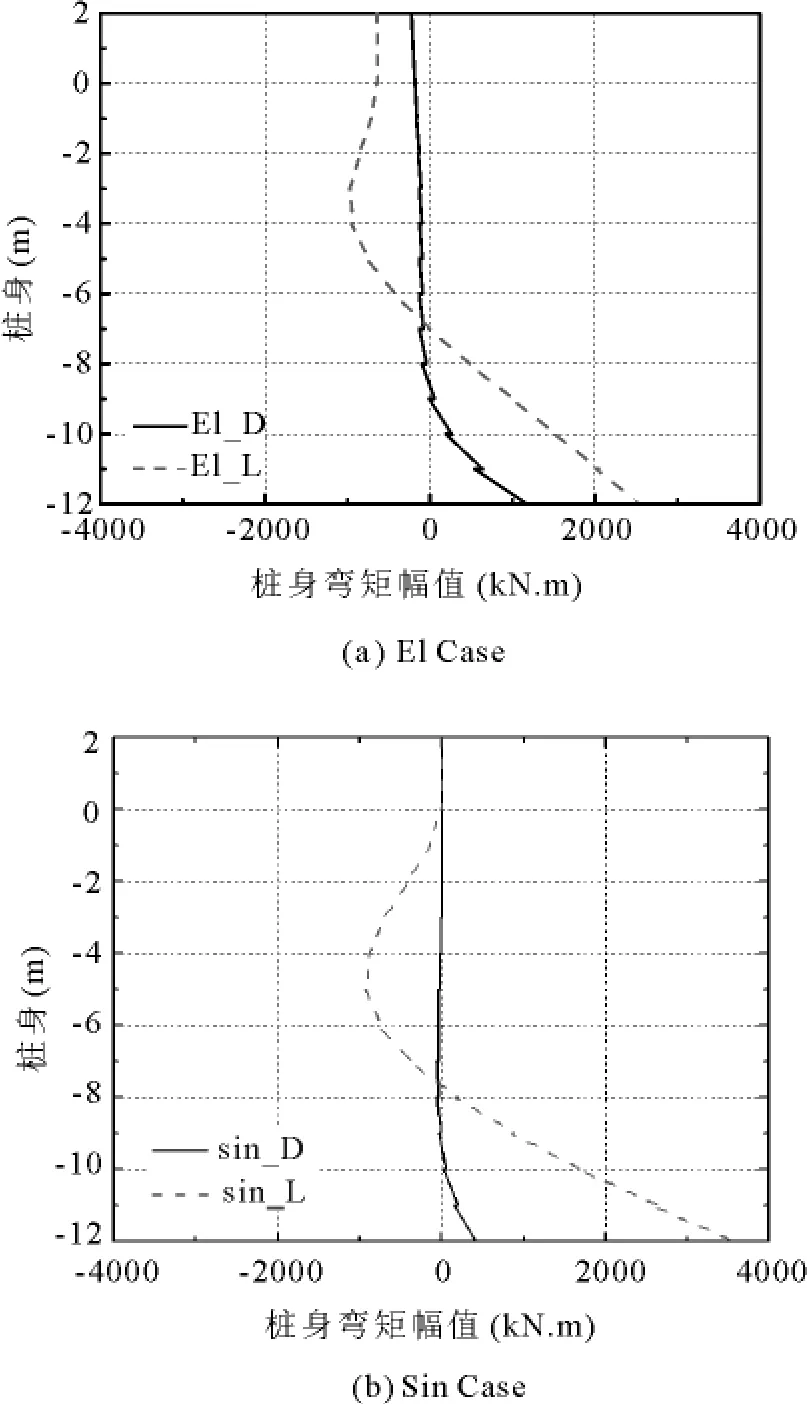
图8 桩身弯矩幅值

2 地震反应

2.1 孔隙水压力

两种波作用下，地表以下4m和6m处沙土的孔隙水压力见图5～6，从图中可以看出:

1、随着场地土深度的增加，极限孔隙水压力增加.

2、在两种波作用下，沙土孔隙水压力迅速增加，且达到液化极限孔隙水压力后并保持恒定，水压力并不随着荷载的减小而减小.

3、El Centro波和正弦波的PGA和频谱不同，说明沙土液化和地震波的种类有关.

2.2 桩身位移幅值和弯矩

两种波作用下，桩身位移幅值和弯矩幅值见图7～8，从图中可以看出:

1、不同地震波作用下，由于PGA和频谱不同，桩身位移和弯矩值不同.

2、沙土液化后，提供给桩的有效水平支撑力减小，的桩身位移远远大于干土的桩身位移，可能导致上部结构的倾覆.

3、沙土液化后，同样由于提供给桩的有效水平支撑力减小，桩身弯矩远远大于干土的桩身弯矩，这样可能导致桩基础地基承载力下降，上部结构倾覆和破坏.

3 结论

本文利用Opensees程序对单桩－沙土相互作用进行地震作用分析，得到以下结论:

(1)孔隙水压力和液化的变化趋势与地震波的类型有关，且达到液化后孔隙水压力保持恒定不随着荷载的减小而减小

(2)沙土液化后，桩身位移和弯矩大幅度增加，可能导致桩承载力降低和上部结构倾覆.

［1］郑新亮，王东升，唐亮.液化场地桥梁基础震害及其抗震研究综述［J］.中外公路，2008，28(4):178－181.

［2］刘惠珊.1995年阪神大地震的液化特点［J］.工程抗震，2001，1(1):22 －26.

［3］吕西林.复杂高层建筑结构抗震理论与应用［M］.科学出版社，2007.

［4］凌贤长，王东升.液化场地桩—土—桥梁结构动力相互作用振动台试验研究进展［J］.地震工程与工程振动，2002，22(4):51－59.

［5］S.Mazzoni，F.Mckenna，M.Scott，et al.OpenSees Command Language Manual［M］.2006:11 －31.

［6］E.Parra.Numerical Modeling of Liquefaction and Lateral Ground Deformation Including Cyclic Mobility and Dilation Response in Soil Systems［D］.Ph.D.Dissertation，Rensselaer Polytechnic Institute.1996:85 －101.

［7］Z.Yang，A.Elgamal，E.Parra.A Computational Model for Cyclic Mobility and Associated Shear Deformation.Journal of Geotechnical and Geoenvironmental Engineering［J］.2003，129(12):1119－1127.

［8］M.A.Biot，D.G.Willis.The Elastic Coefficiects of the Theory of Consolidation.Journal of Applied Mechanics［J］.1957，1(24):594－601.