用β粒子验证动量与动能相对论关系实验数据处理的程序化①
2012-08-21张玉军孙凯霞
张 菲, 张玉军, 孙凯霞
(哈尔滨学院理学院物理系,黑龙江哈尔滨150086)
0 引言
在用β粒子验证动量与动能相对论关系实验中,实验数据的处理方法主要有平均磁场法和主径迹法,其中平均磁场法即认为整个磁场是完全均匀的,这种方法要求学生对每一个数据都要经过反复的代入和修正,并且学生通常利用计算器手工处理实验数据,数据处理比较繁琐,计算量很大.主径迹法是实验仪器上配套软件所提供计算方法,该方法计算结果较为精确,但是这种方法不利于学生对该实验的理解和掌握.同时这个实验对教师来说,批改实验报告的难度也很大,因为学生的数据是在一定的范围内不定点测量所得到的,而且计算过程复杂,中间数据较多,一旦结果有误,教师很难发现问题出现在哪里.然而利用Matlab,并选择适当的计算方法进行编程来处理实验数据就可以解决上述学生和教师所遇到的问题.本文旨在介绍通过Matlab对该实验数据处理过程进行编程的新方法.
1 实验装置及实验数据
实验采用同济大学RES系列相对论效应实验谱仪[1-3],实验数据选用 RES 系列相对论效应实验谱仪教学实验指书中的数据.对NaI(T1)闪烁探测器的能量定标数据和单电子动能和动量的测量数据分别如表1和表2所示.
其中β源的位置为X0=10cm、平均磁场为642.8Gs.Xi为NaI(T1)闪烁探测器测量位置,Ri为回转半径,CHi单能电子峰道数.
2 实验数据处理
2.1 能量定标
利用Matlab中提供的多项式拟合函数polyfit[4]对表1数据进行一次多项式拟合,拟合的结果为
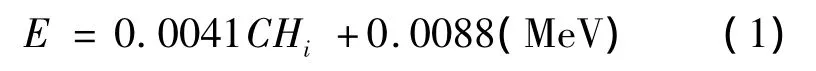
该式就NaI(T1)闪烁探测器的能量定标曲线.
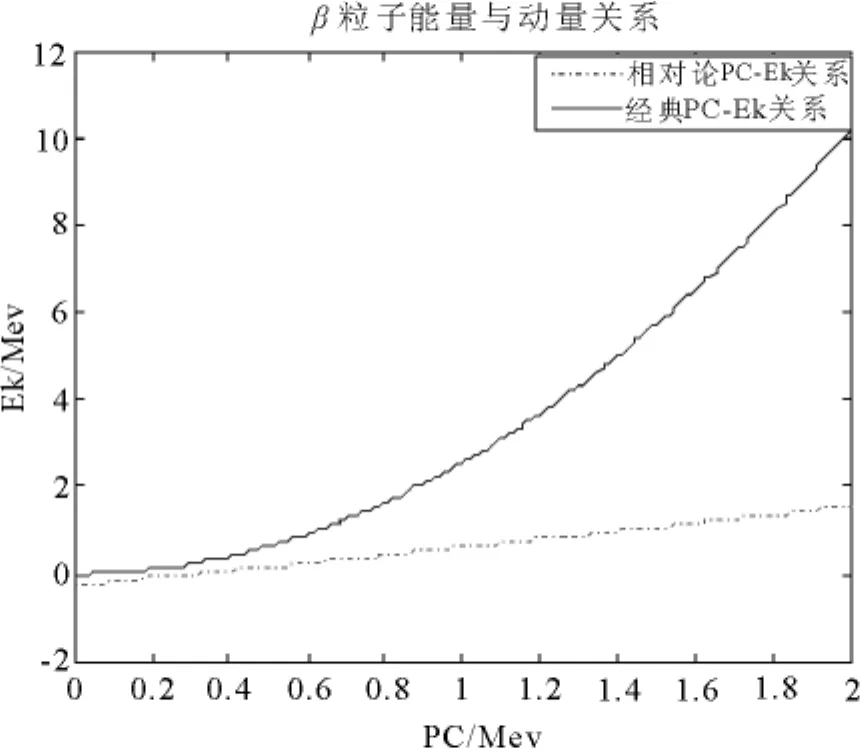
图1 动量与动能关系
2.2 单能电子动能和动量测量
利用Matlab中提供的多项式求值函数polyval函数,将表2数据中的Chi数值代入能量定标曲线得出未经任何能量损失修正的能量E2.再分别利用polyfit对β粒子在Al膜中的能量损失修正表和在有机塑料薄膜中的能量损失修正进行拟合,最终得出β粒子的动能Ek.在这里采用拟合方法要优于采用插值方法,原因在于拟合方法可以扩大修正表的范围,而插值方法是被限定在修正表范围内的.假如当采用插值的方法时,一旦定标数据不准确,可能导致得出的能量E2不在修订表的范围内,这样将使实验数据结果无法处理.并且笔者对两次修正进行不同拟合方式组合的尝试,得出这样的结论,两者均采用二次多项式拟合得出的结果最为理想.

表1 NaI(T1)闪烁探测器的能量定标数据
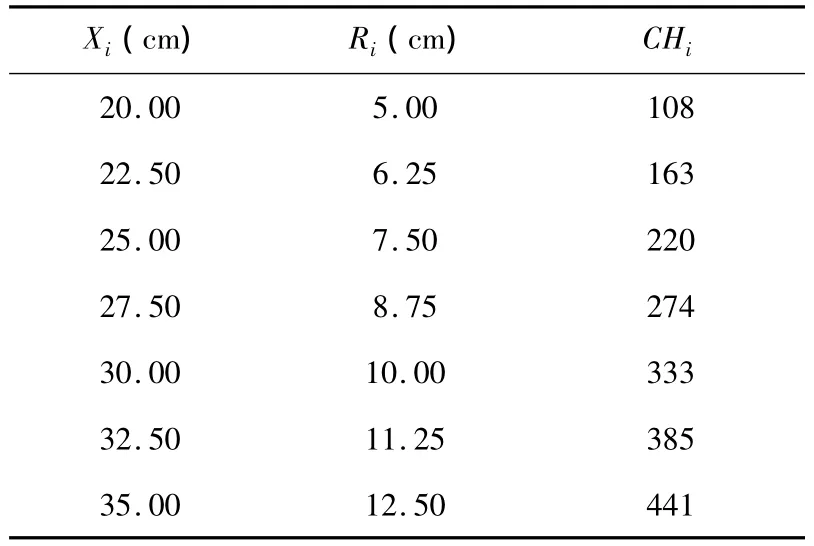
表2 单电子动能和动量的测量数据
2.3 PC的理论值PCT与实验值PC的计算
根据β粒子动能由动能和动量的相对论关系求出动量PC(为与动能量纲统一,故把动量P乘以光速,这样两者单位均为MeV)的理论值
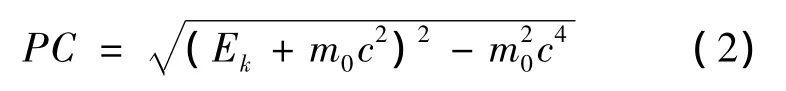
将修正后的β粒子动能分别代入(2)式中即可得到动量的理论值.
对β粒子的动量和动能进行经典计算,采用平均磁场法得出
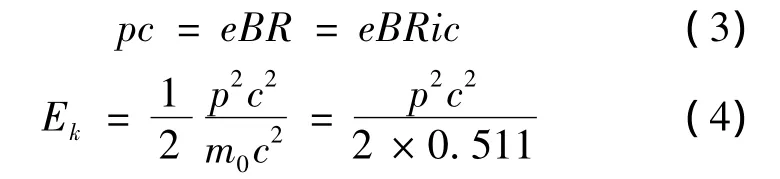
再将回旋半径Ri代入(3)式,再将代入(4)式便可以得到β粒子动能和动量的实验值.
相对误差为
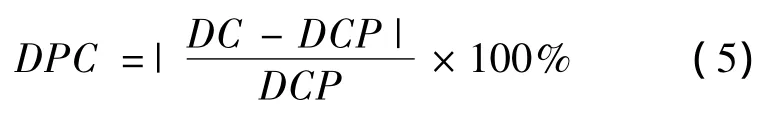
2.4 计算结果与比较
利用Matlab编程,当程序运行之后,输入上述的实验数据,即可得到如表5所示的实验结果和图1所示动量与动能关系曲线.其中DCP’为RES系列相对论效应实验谱仪教学实验指书中的数据处理结果[1],通过比较可以看出,运用本程序所得到的相对误差DCP要明显好于DCP’.而且从运算速度和准确性上都要明显优于手动计算.
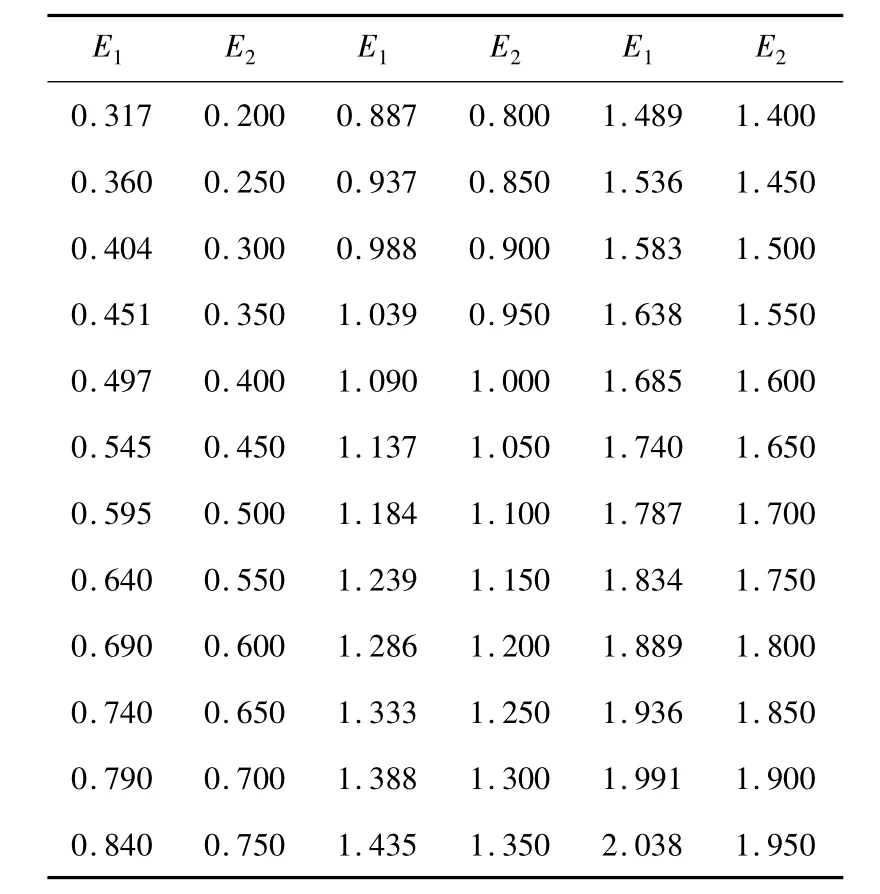
表3 β粒子在Al膜中的能量损失修正表(MeV)

表4 β粒子在有机塑料薄膜中的能量损失修表
2.5 程序的代码
clear
CHi=input('请输入定标道数 CHi= ')
CHi2=input('请输入 β 粒子道数 CHi2= ')
Ri=input('请输入β粒子回转半径 Ri=')
c=2.99*10^8;%光速
b=0.06428;%磁场强度
E=[0.662,1.17,1.33];%定标能量
ab=polyfit(CHi,E,1);%能量定标拟合
E2=polyval(ab,CHi2)% 未经任何能量损失修正的能量E2
e1=[0.2 .25 .3 …… 1.851.91.95 ];%β 粒子
在Al膜中的能量损失修正表E2
e2=[.317 .36 .404 …… 1.936 1.991 2.038];β粒子在Al膜中的能量损失修正表E1
q1=polyfit(e1,e2,2);对β粒子在Al膜中的能量损失修正表进行二次多项式拟合
E1=polyval(q1,E2)%E1
e01=[.365 .581 …… 1.557 1.747];% β 粒子在有机塑料薄膜中的能量损失修表E1
e02=[.382 .581 …… 1.567 1.752];β 粒子在有机塑料薄膜中的能量损失修表E2
q2=polyfit(e01,e02,1);%对β粒子在有机塑料薄膜中的能量损失修表进行二次多项式拟合
Ek=polyval(q2,E1)%Ek
PCT=((Ek+0.511).^2 - 0.511.^2).^0.5;% β粒子动量理论值PCT
PC=b*c*Ri*0.01*10.^(-6);% β 粒子动量实验值PC
DPC=100*abs(PC-PCT)./PCT%相对误差
PT=polyfit(PCT,Ek,2);% 绘制相对论与经典动能与动量关系曲线
Eki=polyval(PT,[0:0.01:2]);
plot([0:0.01:2],Eki,'r- .')
hold on
P=polyfit(PC,(PC.^2)./2*5.11,2);
Ekij=polyval(P,[0:0.01:2]);
plot([0:0.01:2],Ekij)
P=polyfit(PC,(PC.^2)./2*5.11,2);
Ekij=polyval(P,[0:0.01:2]);
plot([0:0.01:2],Ekij)
3 结束语
在用β粒子验证动量与动能相对论关系实验中,采用多项式拟合的算法,并通过利用Matlab对整个计算过程进行编程来处理繁琐的实验数据,这种实验数据处理的程序化,不仅避免了传统手算方法的计算量过大且精确度低,同时也消除了同类软件的全自动化过程对教学中的不良影响,即减轻了教师批改实验报告的负担,又可以在编程的过程中使学生更好的理解实验实验数据的处理过程,而且使数据的处理解更科学,结果更准确.
[1]同济大学物理系,RES系列相对论效应实验谱仪教学实验指导书,2001:30-35.
[2]陈玲燕,顾牧,秦树基等.相对论效应实验谱仪的系列教学实验[J].物理实验,2000,20(3):3-5.
[3]耿完桢,赵海发,大学物理实验[M].哈尔滨:哈尔滨工业大学出版社,2008:340-346.
[4]王正林,刘明.精通MATLAB[M].北京:电子工业出版社,2011:222-223.
