渐开线圆柱齿轮MATLAB建模及其有限元网格的自动划分①

郑 旖， 张为民

(同济大学中德学院，上海200240)

0 引言

齿轮是机械传动中的重要零件.例如在转向器中，由转向轴带动小齿轮旋转，同时和齿轮啮合的齿条做直线运动，带动转向轮转向.因此对齿轮的受力和运动分析显得尤为重要.近年来用有限元方法对齿轮和齿条进行分析和仿真得到了广泛的应用.在使用有限元分析是首先要在齿轮表面进行网格划分.

由于齿轮齿型表面等几何要素通常可用数学解析式来表达，在进行机械特性等分析时，可以不依赖于昂贵专用的UG，Pro－e等三维建模软件.本文利用Mathworks公司的Matlab软件应用面向对象的编程方法，可以在不修改程序的基础上生成齿面轮廓不同的齿轮的网格，从而大大提高网格生成的效率.所开发软件具有将生成的节点和三角形单元数据写入STL或者SHL格式的文件中的功能，从而使得该有限元网格可导入ADAMS中进行运动及受力分析，实现从建模到仿真的数据一致性.

1 渐开线圆柱齿轮单齿的齿形

最常见的齿轮为渐开线圆柱齿轮.一般的渐开线齿轮的单齿平面齿形如图1所示.

CD为齿顶圆弧，BC和DE为渐开线，AB和EF为齿根圆弧.

1.1 渐开线的参数方程

如图2所示，曲线AB为一段渐开线，α为渐开线压力角，rb为基圆半径，φ为渐开线从基圆开始旋转过的角度，φ0为起始角.渐开线上一点A有:

其中:

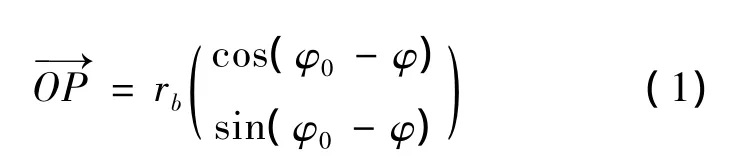
图1 渐开线单齿齿形

1.2 渐开线圆柱斜齿轮的参数方程

图3是斜齿轮的示意图，直径为d的斜齿轮的螺旋角为β，半径为r.此时齿面的初始角φ0(z)=φ0(0)－ δβ·z.其中.所以斜齿轮的参数方程如下所示:

图2 渐开线

图3 斜齿轮

1.3 齿顶圆弧和齿根圆弧的参数方程

齿顶圆弧和齿根圆弧位于齿顶圆和齿根圆上.容易得到齿顶圆和齿根圆的参数方程为:

其中ra，rf分别为齿轮的齿顶圆和齿根圆半径.

图4 各个类及子类的关系

图5 齿轮齿形截面示意图

图6 齿轮三维模型

2 基于MATLAB面向对象的程序设计实现任意齿轮的齿形建模

2.1 MATLAB面向对象的程序设计

MATLAB是一种专业的计算机程序，被广泛的运用于工程中［3］.面向对象的程序将对象作为程序的基本单元，将程序和数据封装其中.MATLAB从版本6.5开始也引入了面向对象的程序设计.

齿轮齿形的各个组成曲线可作为类封装在MATLAB中.任意形状的齿轮只需调用不同的类即可将其齿轮模型建立.

图7 有限元节点生成函数的流程图

图8 平均分布的节点

2.2 MATLAB 类的建立

根据齿轮齿形所构成的曲线，以下几个类将被建立:

1)基础类 @linie.@linie类作为所有曲线的基础类.其输入参数为x和y.(x，y)描述曲线上任意一点的坐标.@linie类下有 mirror，array，extrude，translation等函数，可实现镜像，圆形阵列，拉伸和平移等功能.

2)@linie的子类，如圆弧类@circle，渐开线类@involute，直线类@s_linie等.这些类的输入参数各有不同，如@circle的参数是起始点和终止点所对应的圆角以及圆弧半径，@involute的输入参数是渐开线起始角φ0，起始点和终止点有对应角度φ以及基圆半径rb.这些类也包含mirror，array，extrude，translation等函数，这些函数可以调用父类@linie下的对应函数.

3)@halftooth类.该类描述的是单个齿形分成对称的两部分之后的其中一半.这个类的输入参数为所构成齿轮齿形的各条曲线，如齿根圆弧cf(@circle)，渐开线in(@involute)，齿顶圆弧ca(@circle).该类下 mirror，array，extrude，translation等函数调用各个曲线类下的对应函数.

4)@tooth类.作为@halftooth的子类，@tooth的输入参数为对称齿形的两个对称部分ht1，ht2(@halftooth).该类也继承了@halftooth的所有函数.

5)@pinion.@pinion是@tooth的子类，描述@tooth经过圆形阵列后得到的齿轮平面齿形.其中，输入参数为齿轮的模数m，齿数z，压力角α，齿顶高系数ha，顶隙系数c，变位系数x等.

6)@pinion3D.@pinion3D是@pinion的子类，继承了@pinion的所有参数，其他输入参数还包括螺旋角以及齿轮长度z2等.

各个类之间的关系如图4所示.

构建由齿根圆弧，渐开线，齿顶圆弧所构成的简单齿形.根据建立的类结构写出各类的二维绘图函数plot以及三维绘图函数surf.利用plot和surf函数可画出齿轮的二维和三维图形.对于模数m=2.1374，齿数 z=9，分度圆压力角 α =26.490°，齿顶高系数ha=1.2，顶隙系数c=0.5，变位系数x=0.6 的齿轮，螺旋角 β =20.6589°，齿轮长度b=25.7502生成的二维和三维模型如图5和图6所示.

3 齿轮三角形网格的自动生成

3.1 齿轮有限元网格节点的自动生成

在划分有限元网格之前首先要生成网格节点.由于齿形模型的建立使用了面向对象的编程，因此生成网格节点时分别在组成齿轮轮廓的各条曲线上生成.网格节点生成函数的流程图如图7所示，其中iblKnoten为生成网格节点的函数.

图9 β＜0时生成的三角形网格

3.2 网格节点数量及分布

在确定节点坐标之前，要确定每段曲线上的节点数量和位置分布.如果将曲线划分成n段，那么生成的节点数为n+1个.

按照平均分布来确定曲线上的节点位置.平均分布也就是按照曲线参数平均划分曲线.比如圆弧和渐开线f=g(φ)，平均划分角度φ来得到节点，如图8所示.将曲线平均分成4段生成了5个节点.

图10 β＞0时生成的三角形网格

图11 自动生成的有限元网格

3.3 节点的自动编号

节点的自动编号原则是:

1)在z坐标方向上值最小的一个剖面上选取一个节点编为p(1，1)，该节点所对应的角度为φ0，从这个点开始在z=z1平面上延逆时针方向编号，每生成一个节点编号的第二维加一，直至p(1，n).

2)从z=z1开始沿z轴正方向在z=z2上选取下一个剖面.取 φ = φ0－tan(δβ)·(z2－z1)所对应的节点为 p(2，1)，并且逆时针编号至 P(2，n).如此沿z轴编号直至P(m，n).这样共生成了m×n个点.

3.4 三角形网格的划分原则

三角行网格的划分原则是:

1)生成每条边的两个顶点的编号在某一维上相差1.

2)尽量将三角形划分成锐角三角形.因为三角形精度的计算和三角形最长边和最短边的比有关，比值越小精度越大.钝角三角形的最长边和最短边的比比锐角三角形最长边和最短边的比要大，因此在划分三角形网格是尽量要划分成锐角三角形［4］.

3.5 网格的自动生成

找到相邻的四个节点p(i，j)，p(i+1，j)，p(i，j+1)，p(i+1，j+1).对于不同的螺旋角β，这四个点所组成的四边形不相同.图10所示的是β＜0的情况，图11所示的是β＞0的情况.由于要生成锐角三角形，在β＜0时，生成三角形p(i，j)p(i+1，j)p(i，j+1)和三角形 p(i+1，j)p(i+1，j+1)p(i，j+1)，如图9所示.在β＞0时，生成三角形p(i，j)p(i+1，j)p(i+1，j+1)和三角形p(i，j)p(i+1，j+1)p(i，j+1)，如图10 所示.

取i的值从1到m －1，取j的值从1到n－1，既可生成全部三角形网格.

根据以上方法，在每段曲线上，即齿顶圆弧，齿根圆弧以及渐开线，插入平均分布的五个节点，生成的网格如图11所示.可以看到，此时生成的格的是比较粗略的网格.但是只需要曲线中插入的更多节点，即可生成精度各不相同的网格.另外齿顶圆弧，齿根圆弧以及渐开线等各段曲线上节点数也可各不相同.这样可以适应有限元分析时的不同要求.因为渐开线段的网格质量往往要求比较高，这种情况下只需在渐开线上生成更多的节点即可满足要求.

4 结束语

以齿轮的基本参数为基础，使用MATLAB面向对象的编程方法，可以建立任意轮廓的直齿轮或斜齿轮的二维和三维模型.而基于对象的网格节点生成方法，可以更加快捷灵活的生成所需的节点.点数可以任意增加，也就可以生成足够精度的曲线以及三角形有限元单元.在此基础上也可以方便的更改网格精度来适应不同的需求.

［1］李柱国.机械设计与理论［J］.北京:科学出版社，2003.

［2］Heinz Linke，Stirnradverzahnung:Berechnung － Werkstoffe－Fertigung［J］.Fachbuchverlag Leipzig，1996.

［3］Stephen J.Chapman，MATLAB Programming for Engineers［J］.CL Engineering，2007.

［4］赵军，变速器有限元网格的自动建立［J］.汽车技术，2011(4):38－42.