基于模糊控制理论的越野车辆驱动力控制算法研究

李 睿，李春明，吕建国

(1.中国北方车辆研究所，北京 100072;2.兵器科学院，北京 100048)

越野车辆是汽车领域中一个重要的分支，在民用、军用、竞速、工程勘探等领域中扮演着极其重要的角色，越野车结构简单、结实、通用性强，能在各种地形上行驶，可以完成繁杂的任务.越野车辆的技术核心是对驱动力的管理和控制，最早的越野车辆通过差速锁和高摩差速器来完成这一目标.随着电控技术的大力发展，ABS技术成为汽车的标配产品，同时其逻辑引申产品ASR(驱动防滑系统，或称TCS)也进入到了越野车配置列表中，与传统的中央差速器配合，形成了新的驱动力管理系统，如奔驰的4Matic技术，宝马的X-drive技术、大众的4motion技术、奥迪的quattro技术等.他们的基本原理类似，都是通过一个高性能的轴间限滑差速器来调节前后桥的扭矩分配，或者是采用一个电控的离合器来调节;对于单一车桥的某一侧车轮打滑问题，则通过电控的驱动力管理技术进行干预.

现在多数采用制动力控制的驱动力控制系统是传统的ABS/ASR系统功能的扩展，所以其控制方法多沿用成熟的逻辑门限控制方法，这种以滑移率门限控制为主，以加速度门限控制为辅的联合控制方法，能够有效地遏制车轮滑转趋势，同时辅助参数的引入能够使增、减压控制切换更精确[1-2];另外PID控制和滑模变结构等控制方法也大量地在滑移率控制上开始进行试验[3-4]，取得了良好的效果，有效减小了系统颤振.而模糊控制理论模仿人脑的思维方式，运用模糊数学把人工控制策略用计算机实现，调试起来简单，对与轮胎路面的非线性系统反应也不是很敏感，鲁棒性较好，可以有效提升控制效果[5-7]，模糊控制具有以下几个特点:1)不需要掌握被控对象的数学模型;2)易于实现对不确定性的或者具有非线性的对象进行控制;3)对被控对象某些参数的变化具有较强的鲁棒性;4)对于被控对象受到的扰动具有较强的抑制能力.

本文所研究的驱动力的管理和控制算法，结合了模糊控制理论的知识，针对低速越野时越野车辆某一车桥单侧车轮的打滑问题，在不挂差速锁，并且不降低发动机节气门开度的情况下，通过合理适时的制动力控制，来调整打滑车轮的滑移率，以最大限度地发挥出同一车桥对侧车轮的功率.

1 控制策略及算法

模糊控制器包括状态监测、滑移率计算模块和模糊控制模块，工作流程如图1所示.

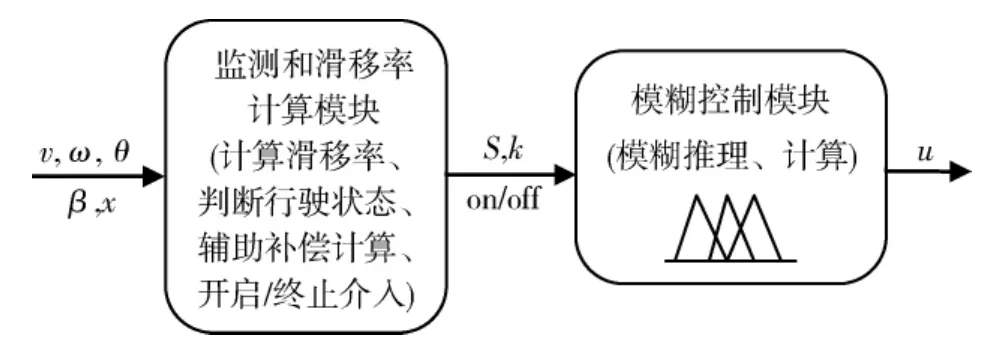
图1 控制器工作流程图

1)监测和滑移率计算模块.该模块需要采集从传感器传来的数据信号，加以计算和分析后，判断进行控制的时机，并将信息传递给模糊控制模块.主要接收的信号有:4个车轮的角速度ω，汽车车速v，方向盘转角θ(用以在转弯的时候补偿计算)、刹车踏板位置x(用以在制动时关闭系统，不与ABS控制器冲突)、水平角度β(在汽车爬坡时调整控制策略，减少打滑时间).由于在汽车驱动过程中，滑移率一直在波动，控制开启阈值选取过小，会造成过度操作，影响车辆正常行驶;选取过大，会使汽车打滑时控制效果变差，不能及时进行介入，同时，结束控制的时机也很重要，需要综合考虑同一车桥两车轮的滑移率变化率值、滑移率差值、角速度差值等因素.本文把直线行驶时控制器开启的条件定为同一驱动桥上的两车轮滑移率差值达到15%以上，打滑车轮滑移率误差变化率的绝对值大于1，同时车速应小于65 km/h.

2)模糊控制模块.模糊控制模块实时接收滑移率计算模块传来的信息，如滑移率S和各种补偿计算系数，接到控制开启命令后，根据模糊控制规则进行计算，对制动器进行适当的控制.本文选取滑移率误差值e及其变化率ec为2个输入变量，输入量均为无量纲变量，制动器开启程度u为输出变量，为便于分析，将系统视为连续控制系统，从而有:

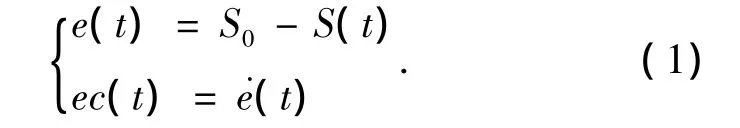
式中:S(t)为车轮瞬时滑移率;S0为期望滑移率.

根据滑移率的取值范围，考虑其他因素的影响，将滑移率误差e的模糊论域取为 [－9，9]，模糊集为 {负大，负中，零，正中，正大}.滑移率误差变化率ec的模糊论域为 [－6，6]，模糊集为 {负，零，正}，输出量 u的模糊论域为[－5，5]，模糊集为 {负大，负中，零，正中，正大}.e和ec的量化因子、输出量u的比例因子均有可变的几个参数可供调用，用以调节系统，避免发散或振荡.然后是选择隶属函数，在误差较小的区域应选择较陡的隶属度函数，提高控制灵敏度;反之在误差较大的区域选择平缓的隶属函数，增强系统的鲁棒性.本文采用马尔蒂尼型控制器，根据Simulink的fuzzy toolbox可以方便地设计出e、ec和u的隶属度函数 (见图2～图4)和控制规则(见表1).

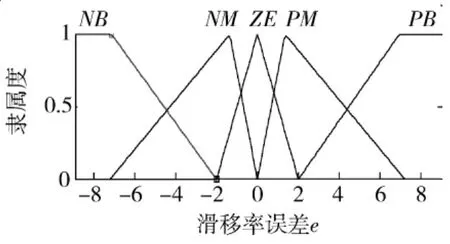
图2 滑移率误差e的隶属度函数

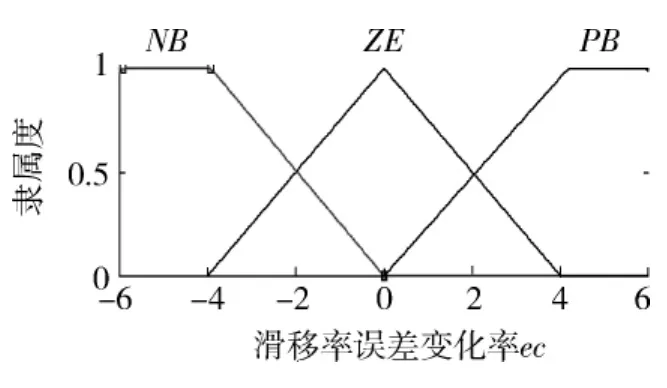
图3 滑移率误差变化率ec的隶属度函数

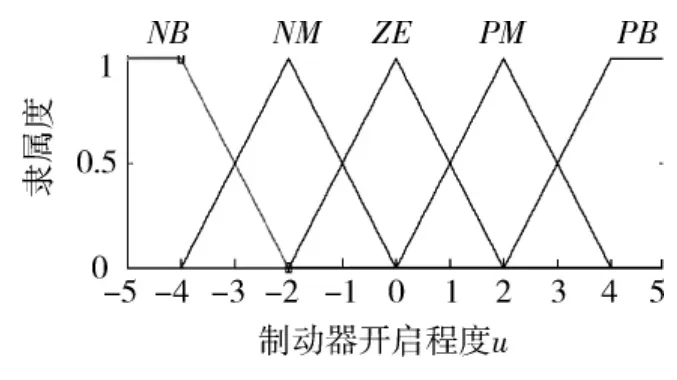
图4 制动器开启程度u的隶属度函数

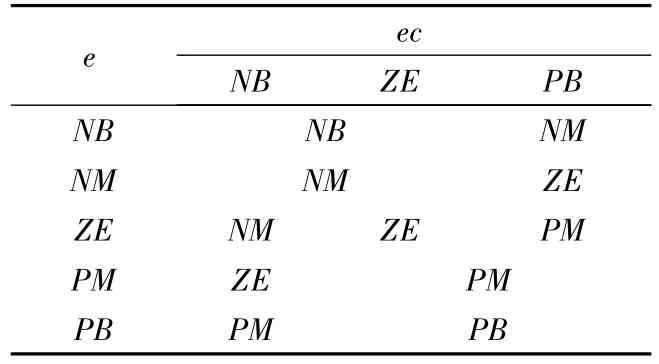
表1 制动器开启程度u的模糊推理规则表

2 模型的建立

通过Simulink(版本为7.11.0(R2010b))建立仿真模型，如图5所示.本文建立的是带有差速器影响的两轮驱动车辆的直驶模型，包含发动机、差速器、轮胎、车辆动力学模型等主要部件.部分参数如下:整车质量为1 500 kg，轮胎滚动半径为0.406 4 m，发动机最大功率为150 kW，最大转速为6 000 r/min，发动机输出轴转动惯量为12 kg·m2，半轴转动惯量为4.129 kg·m2.这里主要介绍轮胎和差速器部分.

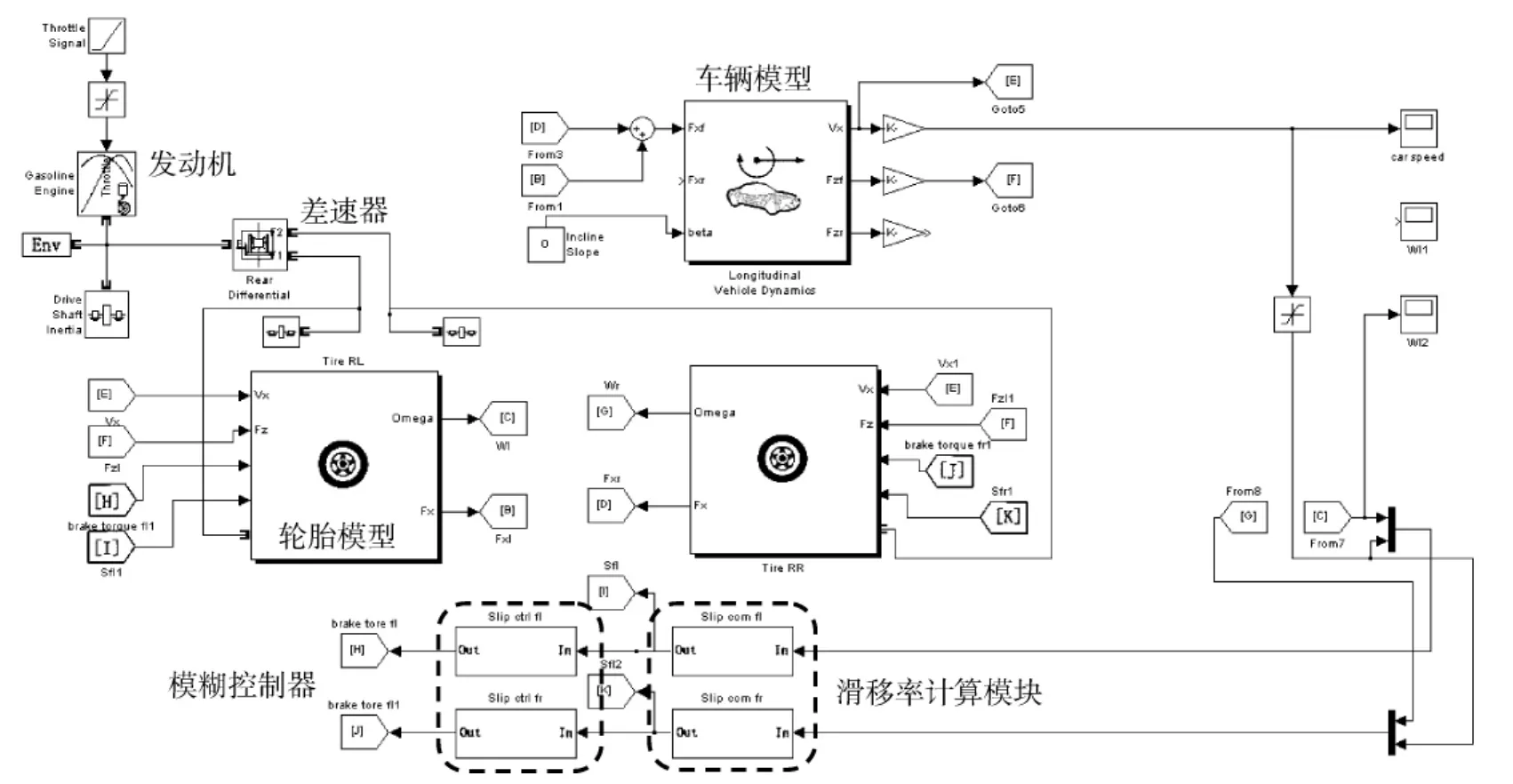
图5 仿真框图

1)轮胎与路面.驱动力控制系统中需要将车轮滑移率控制在峰值附着系数μ对应的最佳滑移率处，这样才能最大限度地利用地面附着力.不同路况下，最佳滑移率是不同的，但相差不太远，最佳滑移率一般在0.2左右，如图6所示[8].

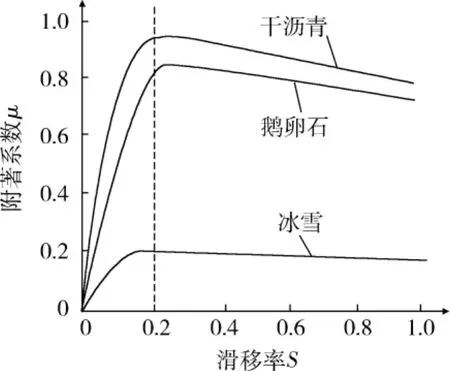
图6 不同路面下滑移率-附着系数曲线图

滑移率的表达式为

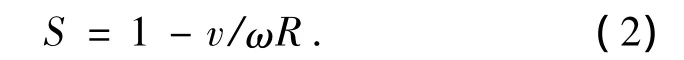
式中:ω为轮胎角速度;R为车轮滚动半径;v为车速.

轮胎与路面模型是在Burckhardt魔术公式模型基础上经过理论变形、仿真分析得到的.假如忽略车辆行驶速度和轮胎载荷的影响，那么纵向附着系数表达式为:

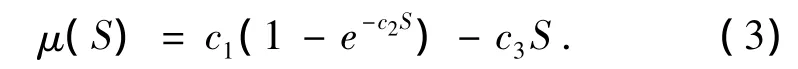
参数c1、c2和c3在各种路面下的取值如表2所示.

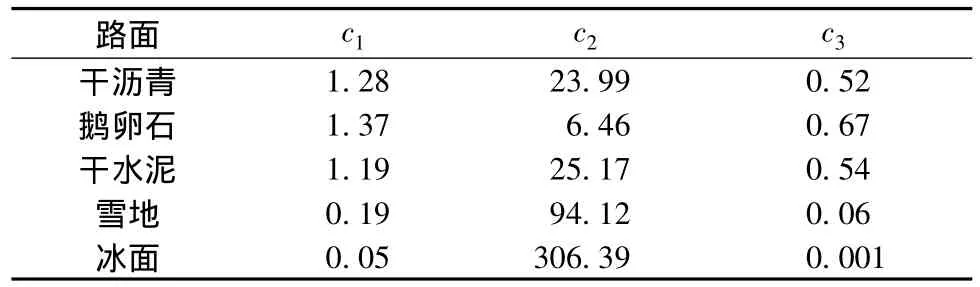
表2 不同路面下的参数值

2)差速器.在普通开式差速器工作时，行星齿轮不仅绕半轴齿轮中心公转，而且还绕行星齿轮轴自转，两半轴齿轮的转速和为差速器壳转速的2倍，如图7所示.

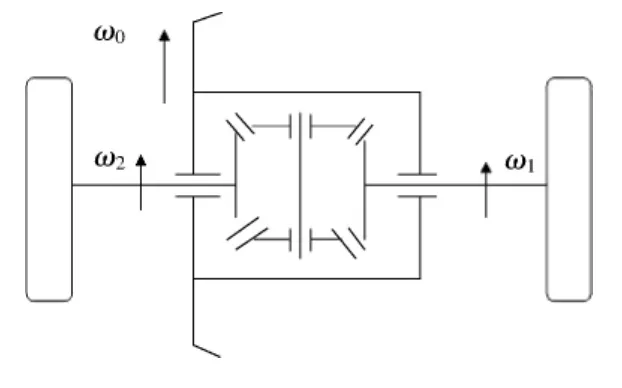
图7 差速器工作原理示意图

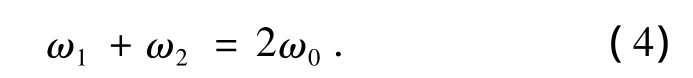
当两侧转速不同时，存在一个使行星齿轮绕其轴转动的力矩Tf(即差速器在相对运动时所产生的且能折合到半轴齿轮上的摩擦力矩).对于慢转一侧的半轴齿轮，Tf和发动机传递到该半轴上的扭矩方向相同，而对于快转一侧的半轴齿轮，Tf的方向正好相反，所以慢转的半轴齿轮所传递的扭矩较大，而快转半轴齿轮所传递的扭矩较小.此时左右车轮上所能产生的总驱动力为:

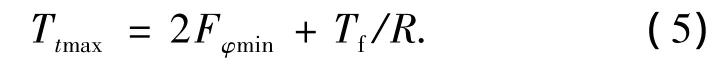
式中:Fφmin为低附着一侧车轮的驱动力.

虽然差速器的内摩擦使汽车的总驱动力增大了Tf/R，但是其工作特性使得当汽车越野行驶在泥泞、冰雪路面上时，如果某一侧的驱动车轮与地面的附着系数很小，即使另一侧驱动车轮与路面有良好的附着性，其驱动轮扭矩也不得不随着附着系数小的一侧同样地减小，使汽车无法发挥出附着良好驱动车轮的潜在驱动力，甚至有陷车的危险，此时即需要驱动力管理系统的辅助.

本文还建立了一个逻辑门限控制器 (根据滑移率误差的正负差值设定若干门限，进行制动器增压、保压、减压操作)以及没有驱动力控制器的车辆驱动模型，并对三者进行对比仿真.

3 仿真分析

1)车辆在对开路面起步，左轮位于低附着路面 (峰值附着系数φ=0.36)，右轮位于良好路面.从仿真结果图8、图9可知，模糊控制下的车辆能显著提速，且系统超调量比逻辑门限小10%，调整时间短1.9 s.

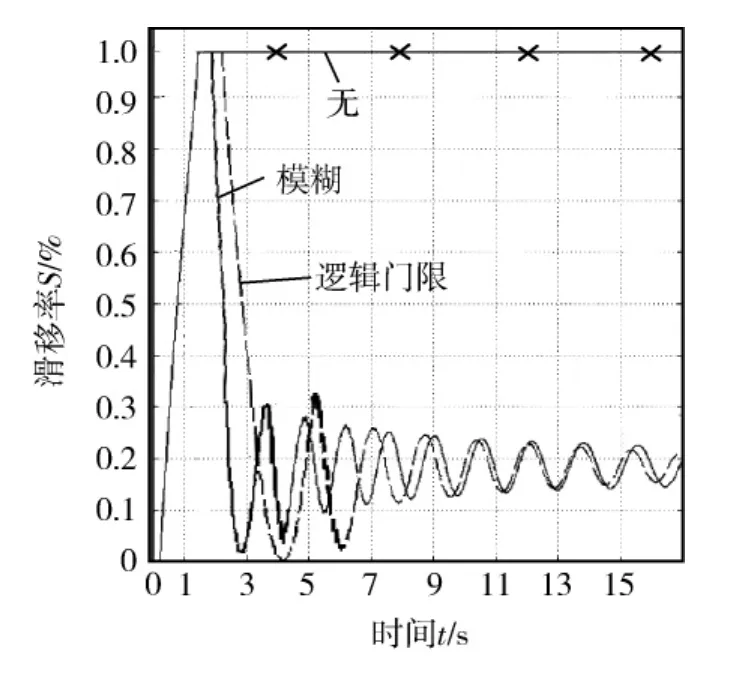
图8 打滑车轮滑移率随时间的变化情况对比1

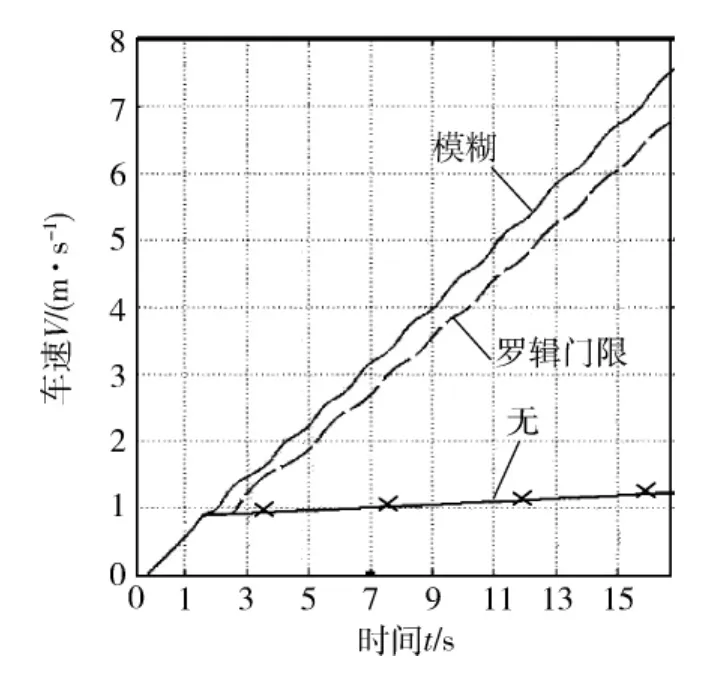
图9 车速随时间的变化情况对比1

2)车辆行进中驶上对开路面，左轮位于恶劣冰雪路面 (峰值附着系数φ=0.18)，右轮位于良好路面.从仿真结果图10、图11可知，模糊控制算法的超调量比逻辑门限控制算法小21%，进入稳定状态的时间短1.2 s.

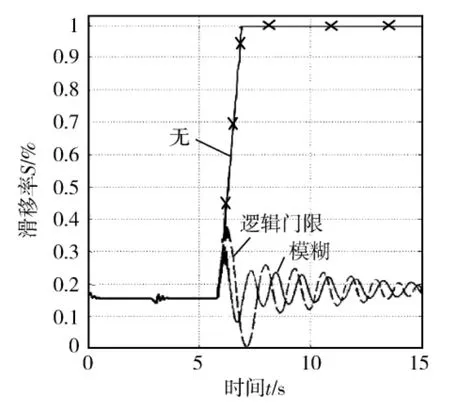
图10 打滑车轮滑移率随时间的变化情况对比2

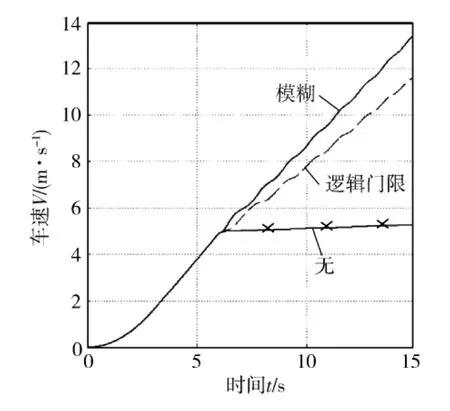
图11 车速随时间的变化情况对比2

3)左轮先行驶在低附着路面后遇到冰雪路面，右轮始终行驶在良好路面.从仿真结果图12、图13可知，在连续遭遇不同附着系数的路面时，模糊控制的鲁棒性较好，对系统的变化敏感度较小，当车辆切换路面和调整最佳滑移率控制点后能很快使系统稳定.

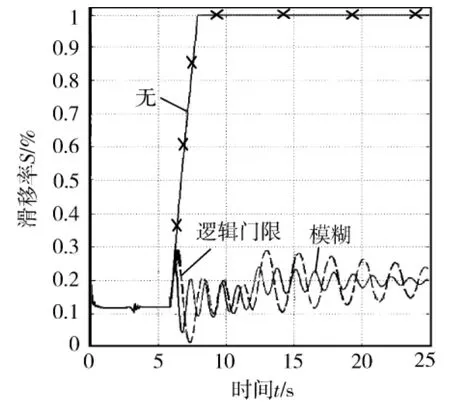
图12 打滑车轮滑移率随时间的变化情况对比3

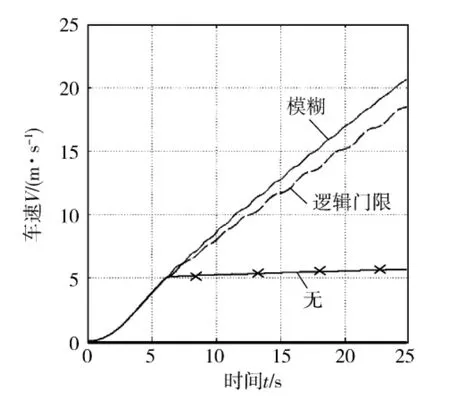
图13 车速随时间的变化情况对比3

4 结论

1)仿真结果表明，在这3种工况下，模糊控制算法可以很好地控制打滑车轮的滑移率，发挥出车辆的驱动力，而且超调量很小，比逻辑门限控制法小15%左右，调整时间短.

2)模糊控制器调试起来简单，适应性好，遇到路面状态切换时有很好的鲁棒性.

3)模糊控制算法还需进一步完善，如引入更多的补偿计算因子以适应各种复杂的工况.还可与路面识别设备匹配以在线调整最佳控制点，等等.

4)需要根据控制理论做成实物控制器，进行进一步的硬件在环仿真，以验证控制算法的合理性.

[1] 高 阳，李 静，赵 健，等.全时四轮驱动汽车驱动轮牵引力综合控制策略 [J].吉林大学学报:工学版，2009，(3):296-299.

[2] 张 为，王伟达，丁能根，等.基于dSPACE的ASR硬件在环仿真平台开发及ECU性能试验[J].汽车技术，2009，(10):4-8.

[3] 李 静，张家财，李幼德，等.汽车驱动防滑转遗传PI控制半实物仿真 [J].系统仿真学报，2006，(7):1972-1975.

[4] 唐国元，宾鸿赞.ABS的模糊滑模变结构控制方法及仿真研究 [J].中国机械工程，2007，(7):1629-1632.

[5] 刘国福，张 玘.汽车防抱制动系统自适应滑模控制算法的研究和半实物仿真[J].国防科技大学学报，2008，(10):125-130.

[6] 王国业，刘昭度，胡仁喜，等.基于等效滑移率变化率的汽车防抱制动系统模糊直接自适应控制[J].机械工程学报，2008，(11):242-247.

[7] 张向文，王飞跃.汽车ABS自适应模糊滑模控制算法研究 [J].汽车技术，2009，(10):25-30.

[8] 余志生，夏群生.汽车理论 [M].4版.北京:机械工业出版社，2007:90-93.