类车体外流场非稳态特性数值研究

2012-08-21杨志刚

空气动力学学报 2012年6期

关键词：尾迹车体稳态

朱晖，杨志刚

（1．上海同济大学地面交通工具风洞中心，上海201804；

2．湖南大学汽车车身先进设计制造国家重点实验室，湖南长沙410082）

0 引言

类车体外流场结构受尾部斜面倾角的影响显著：0°～12．5°情况下，气流附着于尾部斜面上，并于车体背部分离，形成典型的直背构造尾迹区流场结构；随着斜面倾角的增大，在尾部斜面上产生分离泡，车体背部产生分离涡，并伴随流向拖曳涡对的出现。

当尾部倾角为30°时，气动阻力呈现急剧下降的状态，依此为判据，确定30°后倾角为临界状态［1］。目前，针对30°后倾角类车体尾迹区流动特征及流场结构的研究较少，作为临界状态，有必要加以研究。

类车体外流场普遍具有非稳态的特性，然而诸多文献多采用稳态方法或非稳态方法，通过对时均流场结构特点的描述，研究其流动现象，无法有效揭示类车体外流场非稳态运动的变化规律［2－4］。

本文以大涡模拟为手段［5］，监测30°后倾角类车体尾迹区流场部分参数的时变运动信息，对取得的采样数据进行统计分析，在明确其频谱特征的基础上，得出相应结论。

1 几何模型及流场空间离散

［1］（Ahmed等，1984），数值计算采用的类车体模型构造如图1所示。图中，尾部倾角角α为30°，保持不变。

大涡模拟采用过滤方法，将湍流运动分解为可解尺度湍流和不可解尺度湍流运动。由于其基于空间平均的模式构架，决定了大涡模拟对网格尺寸较强的依赖性。

图1 类车体构造（单位：mm）Fig．1 Geometry of Ahmed body（unit：mm）

为了扩大直接数值计算范围，提高截断波数和计算求解精度，尤其是考虑到近壁面尾迹区流场的计算精度，面网格参数如表1所示。

表1 面网格参数Table 1 Parameters of surface mesh

空间计算区域长10144mm、宽4740mm、高3280mm，坐标系设定如图2所示，阻塞比为0．7%。为了减轻数值粘性的影响，整个计算域划分为大小不等的六面体网格。近壁面第一层网格中心离壁面的法向高度，以y＋为1～10加以控制，目的在于：尽量描述边界层层流底层的性质；边界层网格共40层，与外围网格实现了较光滑的过渡连接。体网格总数为1500万单元，内部结构如图2所示。

图2 体网格结构Fig．2 Structure of volume grid

2 数值计算方法

湍流模型采用Smagorinsky模型［6］，该模型是根据唯象论推出的剪切湍流亚格子模型，其原始模式为雷诺平均混合长度模式在大涡模拟中的推广。该模型属于耗散型，因此，在总体上符合湍流输运的性质，且数值上易稳定。唯一的模式系数Cs＝0．14。

迭代方法采用Van doormal和Raithby于1984年提出的分离式SIMPLEC算法。此算法与SIMPLE的计算步骤相同，只是速度修正方程中的系数项d的计算公式有所区别。动量方程采用Bounded central differencing离散格式，压力项采用标准格式。具体过程在Fluent6．3中实现。

时间步长取0．0005s，固定不变。每步迭代次数以计算达到内部收敛为准。为确保数值解的精度，所有监测的流场参数皆满足相应格式的收敛条件。

入口处采用速度入口边界条件，认为速度为均匀分布，U＝35m／s，V＝W＝0m／s，湍流强度1．35%；出口采用压力出口边界条件，表压取0Pa，其它参数与进口类似；地面和车身皆采用无滑移边界条件，计算域回型面采用对称边界。雷诺数Re＝2．5×106。

3 计算结果

3．1 气动力的非稳态特性

气动力集中反映了绕流流场与车体的相互作用，流场运动的非稳态性质势必在车体所受气动力方面得以体现。图3、图4分别为车体所受气动阻力和升力随时间变化的图谱。

由图3、图4可知：随着时间的推进，阻力系数CD和升力系数CL分别在各自的脉动区间内上下波动，体现了较强的周期性特征。其均值分别为0．325和0．521，与实验值符合较好［7］。

时变图谱不能直观反映气动力非稳态特性的频率特征，因此对计算结果进行时频转换。功率谱方法将合成振动的简谐振动特征进行辨析，从而得到清晰的频率分布特性，如图5、图6所示。

图3 阻力系数随时间变化图谱Fig．3 Figure of time－dependent CD

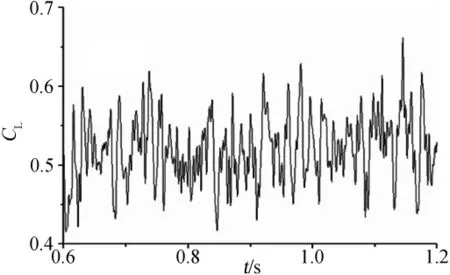
图4 升力系数随时间变化图谱Fig．4 Figure of time－dependent CL

图5 阻力系数功率谱Fig．5 PSD of CD

图6 升力系数功率谱Fig．6 PSD of CL

由图5、图6可知：在频率范围［20，40］Hz内，能量出现峰值，表明绕流流场作用于车体的能量集中于此频率范围；此频率范围也是气流从车体上脱落的特征频率范围。阻力系数和升力系数峰值频率分别为30．0Hz和33．5Hz，其所对应的斯特罗哈数（St＝fd／v）分别为0．287和0．320，略小于文献［8］发表的实验值。

3．2 尾迹区流场的非稳态特性

尾迹区流场的监测点坐标分别为：［1056．5，－97．25，138．5］、［1056．5，97．25，138．5］、［1148．4，－97．25，138．5］、［1148．4，97．25，138．5］、［1357．2，－97．25，138．5］、［1357．2，97．25，138．5］，为两两对应的三组测点，分别记为：point1、point2、point3、point4、point5、point6；离车体背部的相对位置x／L＝0．012、0．1、0．3，式中L为车模长度1044mm。

由于常用的稳态算法、平均流场统计仅描述了流场的定常性质；多数流场实验（尤其是测三维流速）又忽视了流场中空间位置对称处流动参数需同时测量的必要性。所以，对于尾迹区流场的非稳态特性描述不足，尤其是空间对称测点处，三维速度的相位变化特征。

图7为point1和point2两对称采样点处三维速度的功率谱分析结果。由图可知：空间对称测点处三维速度功率谱分析结果类似，在频率范围［0，100］Hz内皆出现能量集中现象；在40Hz附近三个方向速度功率谱皆达到峰值水平。

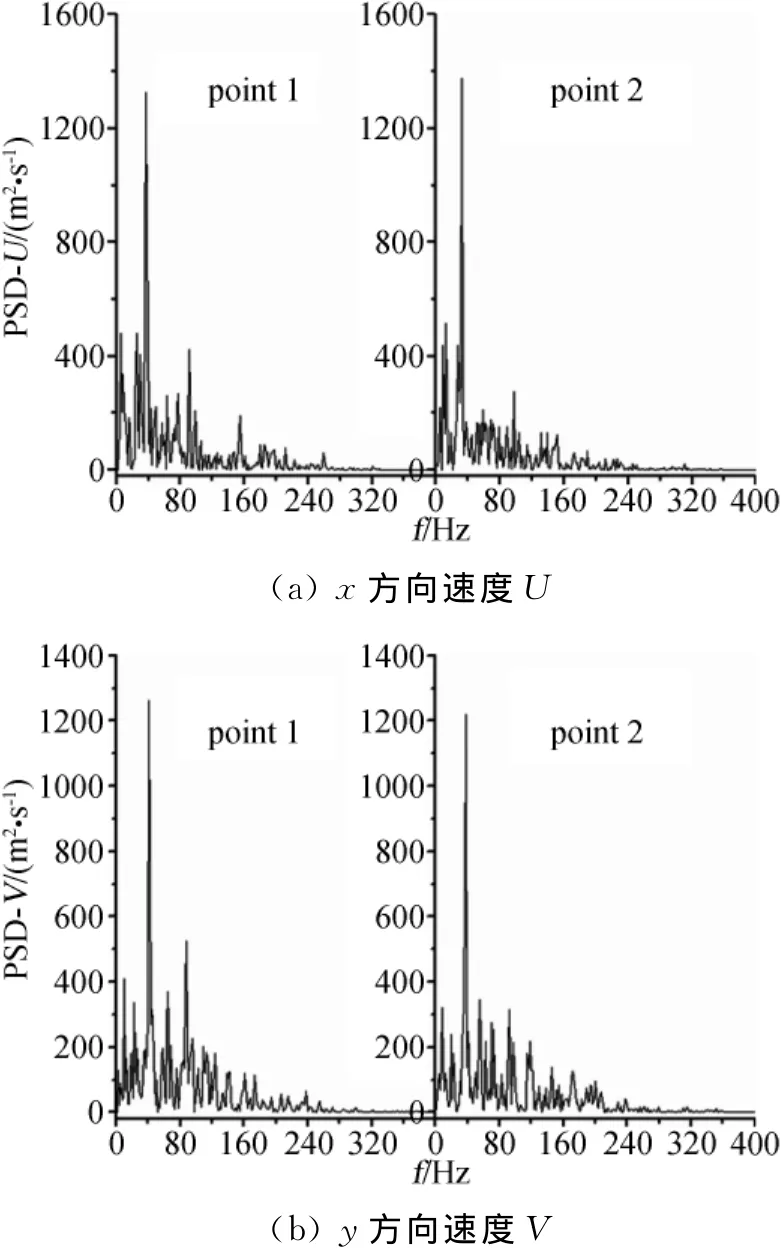
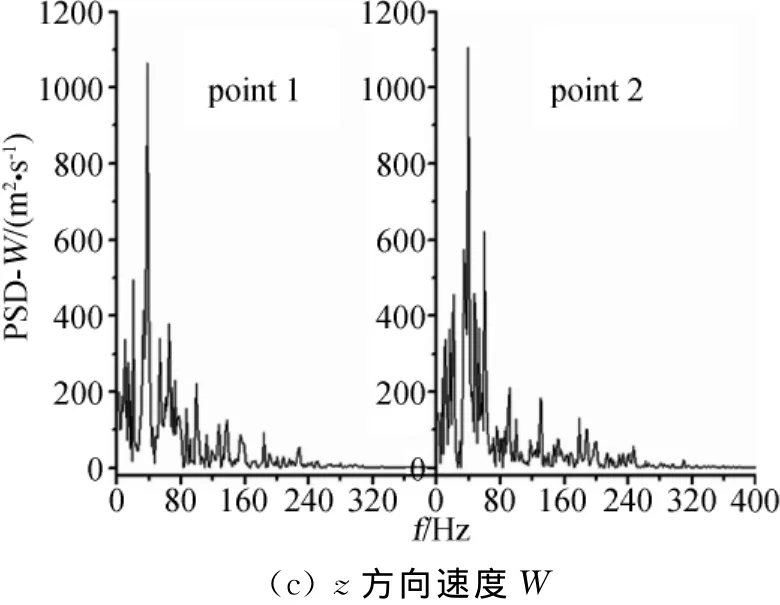
图7 point1与point2三维速度功率谱Fig．7 PSD of 3Dvelocity in point1and point2

point3和point4，point5和point6之间，三维速度的功率谱分析结果与图7类似，所有测点处三维速度功率谱峰值对应的频率值见表2。由表可知：最高频率对应的斯特罗哈数范围［0．306，0．386］，与文献［7］符合较好，且普遍高于阻力系数和升力系数的分析结果。

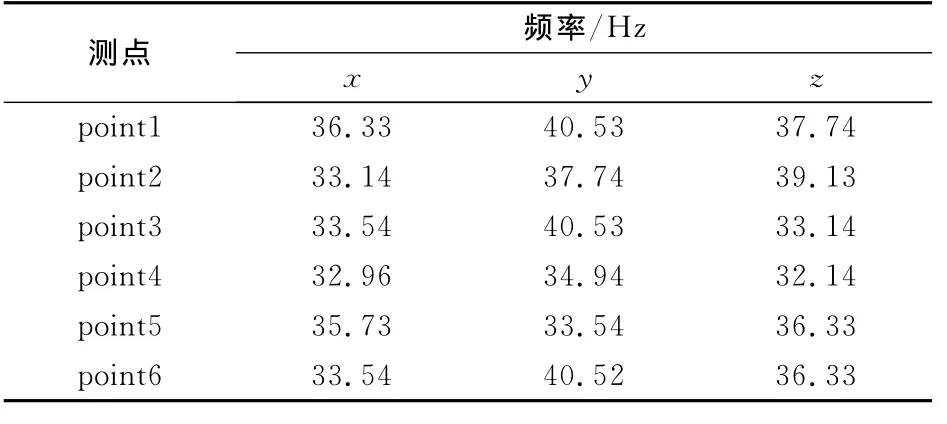
表2 功率谱峰值频率Table 2 Frequence to peak value of PSD

功率谱分析揭示了流场中测点处能量的频谱特性；进而，采用互谱分析，揭示流场中测点间的相位变化规律，如图8～图10所示。

由图8～图10可知，空间对称测点处三个方向速度两两之间存在明显的相位差，且并非常数。相位差在［－180°，180°］范围内上下波动，并不完全为0°或180°，说明三个方向速度两两之间并非完全对称。

图8 x／L＝0．012处速度相位Fig．8 CSDP of velocity at x／L＝0．012

图9 x／L＝0．1处速度相位Fig．9 CSDP of velocity at x／L＝0．1

图10 x／L＝0．3处速度相位Fig．10 CSDP of velocity at x／L＝0．3

在选定测点处，当归一化频率小于0．6时，三维速度两两之间的相位差呈随机分布的特点。当归一化频率大于0．6时，y方向速度的相位差接近于±180°，且随着测点逐步远离车体背面，此规律亦成立；z方向速度的相位差始终在0°附近上下波动；随着测点逐步远离车体背面，x方向速度的相位差逐步呈现为围绕0°上下波动的特点。