一维脉冲爆轰波的能量释放规律研究

滕宏辉，刘云峰，姜宗林

（中国科学院力学研究所高温气体动力学国家重点实验室，北京 100190）

0 引言

爆轰波是激波压缩自点火，燃烧放热支持其高速自持传播的燃烧波。以爆轰波为基础的推进装置具有很高的热循环效率和一些独特的优点，因此可望用于未来的高超声速飞行器。然而，由于缺乏对爆轰物理的深入认识和掌握，将爆轰波应用于航空发动机的努力遇到了巨大的困难，因此需要对爆轰波的基本物理现象和规律进行系统的研究。早期的研究者建立了CJ（Chapman－Jouguet）理论和ZND（Zel'dovich－von Neumann－Doring）模型，对爆轰波的传播速度的计算和实验结果符合的很好［1］。进入19世纪60年代以后，随着实验技术的进步，研究者发现ZND 模型给出的爆轰波结构和实际结果相差很大。气相爆轰波波后通常是湍流燃烧，而且具有复杂的波面结构［2］。这是由于气体流动和燃烧过程的同时存在，导致了气体动力学和化学反应动力学的耦合，而燃烧反应总体放热速率对于温度存在指数依赖关系，因此诱导了爆轰波的不稳定性。爆轰波的不稳定性会导致波后出现横波，进而形成胞格结构。Shepherd等［3］归纳总结了大量的实验结果，给出了氢气、甲烷、乙炔等常见气体在不同热力学参数下的胞格尺度。Gamezo等［4－5］利用Euler方程和单步放热化学反应模型模拟了横波和胞格爆轰的形成和传播过程，发现波后未反应气团的存在和化学反应参数密切相关，较高的活化能有利于形成波后未反应气团，进而导致较复杂的胞格结构。另外，研究者还关注了二维平面［6］和轴对称［7］的斜爆轰波面，发现波面后方也会出现横波结构和振荡燃烧现象。

虽然二维和三维爆轰波的胞格结构反应了爆轰波的内在不稳定性，但是其本质上还是源自激波和燃烧的耦合。因此许多研究者从简单的一维模型出发，对脉冲爆轰波的传播进行了大量研究，得出了许多有意义的结果。Erpenbeck［8］对一维和二维爆轰波进行了稳定性分析，利用渐进理论得到了爆轰波的稳定性边界。He等［9］研究了对活化能对一维爆轰波的影响，发现随着活化能的增加，爆轰波从稳定传播发展为脉冲爆轰波，最后由于震荡幅度过大导致不能稳定传播。Ng等［10］采用两步反应模型发现，放热区长度和诱导区长度的比值决定了爆轰波的稳定性，这个值越小爆轰波越不稳定。Watt等［11］对一维爆轰波稳定性受到曲率的影响进行了理论分析，发现爆轰波对曲率的变化非常敏感，较小的曲率变化就会使爆轰波发生明显的失稳，并得到了进一步的数值验证。洪滔等［12］采用简化的基元反应模型研究了乙烷空气混合气体中的一维爆轰波的稳定性，发现爆轰波的振荡受到计算网格尺度影响很大，在较高密度的网格下得到的振荡波长和实验结果符合较好。

虽然对一维爆轰波不稳定性的研究取得了很大的进展，然而还有许多悬而未决的问题需要进一步研究。以前的研究者采用了许多不同的化学反应模型，发现了一些相似的变化规律。多种模型的结果都显示激波和燃烧耦合强弱是决定爆轰波稳定性的关键因素，并且对于不同的模型可以给出不同的稳定性边界。但是这些稳定性结果主要依赖于化学反应模型的一些参数，如活化能等，而不同模型给出的稳定性条件之间的无法建立直接的对应关系。这是因为爆轰波的传播源于激波和燃烧的动态耦合，而这些静态的参数本身并不能直接描述这种耦合关系，也无法对其进行量化分析。因此，对于爆轰波不稳定性的认识还停留在定性的阶段，从而对一些关键的问题缺乏深入的研究。爆轰波的前导激波在燃烧驱动下的振荡传播是个动态的过程，必须对爆轰波后流场的能量释放过程进行分析，才能进一步从激波和燃烧耦合的角度研究爆轰波的不稳定性。本文采用三步链锁反应模型，对一维脉冲爆轰波进行数值模拟，重点通过对不同爆轰波的振荡传播进行分析，讨论化学反应过程和流体动力学过程耦合下的爆轰波不稳定性，揭示在爆轰波传播过程中的能量释放规律。

1 数值计算模型和方法

爆轰物理的研究通常忽略粘性等因素的影响，控制方程采用无量纲的Euler方程组：

其中ρ、u、p、e分别表示流体密度，速度，压力和总能量。假设气体为具有固定比热比的完全气体，则总能量和状态方程为：

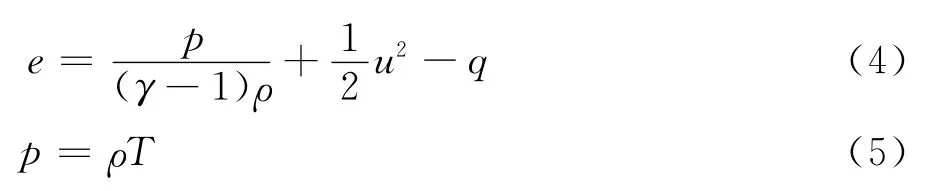
其中T为气体温度，q为化学反应放热量：

其中f和y分别为混合气体中燃料和中间粒子的百分比，将在化学反应模型中给出。上述所有的方程及其变量都利用波前气体参数进行了无量纲化，具体的公式如下：

特征长度和特征时间的定义在化学反应模型中给出。

在爆轰波流动中，需要采用化学反应模型来模拟燃烧过程，从而计算放热量。本文采用了Short等［13］提出的链锁化学反应模型。通常的化学反应模型包括基元反应模型和分步反应模型，前者精度较高但是效率较低，而后者效率较高、物理概念清楚，适于对爆轰物理的现象和机制进行定性研究。链锁反应模型是分步模型的一种，它将化学反应分成三步，分别为链起始反应，链分支反应和链终止反应。和通常的单步及两步化学反应相比，这种模型能够更真实地描述化学反应动力学过程。三步链锁反应模型的主要方程是：

链起始反应：

链分支反应：

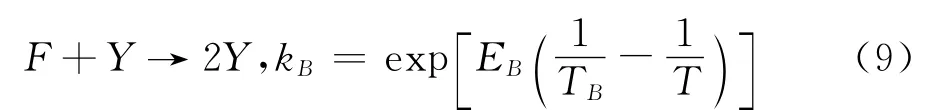
链终止反应：

其中，F，Y和P分别表示燃料、中间粒子和产物。在这个反应模型中，链起始反应和链分支反应对温度的依赖关系遵循Arrhenius定律，而链终止反应具有固定的、不依赖于温度的反应速率，这种设定是符合化学反应实际过程的。式（10）设定链终止反应的速率为1，即隐式地定义了无量纲长度，进而无量纲时间为˜t＝˜x／˜c0。该反应模型中具有EI，EB，TI，TB四个反应参数，其中前两个为起始反应和支化反应的活化能，后两个为反应的跃变温度。如果气体的当地温度达到跃变温度，意味着链起始反应或者链分支反应的速率和链终止反应速率相同，因此这两个参数的设定对于反应模型非常重要。参考以前的研究模型［13－14］，本文采用的模型计算参数为Q＝8.33，γ＝1.20，EI＝37.5，EB＝10.0，TI＝3TS，其中TS是爆轰波的前导激波后方的温度。上述所有参数都是采用公（7）无量纲化之后的参数，这组参数物理上对应于低压气体中较低马赫数的爆轰波。爆轰波的稳定性通过可变参数TB控制，主要作用于链分支反应的速度，该参数对爆轰波动力学过程的影响是本文重要的研究内容。在下文中的采用“模型跃变温度”指代TB／TS，作为研究爆轰波不稳定性的分叉参数。另外，采用了MUSCL－Hancock格式［15］对Euler方程进行离散，并将流动和化学反应解耦，对化学反应采用显式方程求解。

2 计算结果与分析

2.1 脉冲爆轰波的传播和数值结果验证

以前的研究表明，一维爆轰波既存在稳定传播的理想的CJ爆轰波，也存在非稳定传播的脉冲爆轰波。图1显示了三种典型的爆轰波传播过程。计算的初始条件采用相应参数下的一维CJ爆轰波，将其放置在左侧流场中。由于理论解和激波捕捉格式得到的数值结果在激波面附近存在初始误差，会触发爆轰波的不稳定性。不同的模型跃变温度对应不同的化学反应速率，进而形成了不同特性的爆轰波。采用跃变温度为0.88时，初始的扰动导致爆轰波的传播过程中发生了振荡，但是随着传播距离的增加振荡消失，爆轰波逐渐发展成为稳定的CJ爆轰波。采用跃变温度为0.90时，在初始扰动形成的振荡之后，爆轰波逐渐发展成为具有更大振幅的周期性振荡。这种新的振荡模式具有固定的振幅和周期，爆轰波的传播速度、波后压力等参数围绕CJ状态的速度和压力进行振荡。采用跃变温度为0.92时，在初始扰动的诱导下，爆轰波形成了双模振荡。这种情况下爆轰波的振幅更大，周期也更长，而且形成了两个不同的压力极大值和极小值。因此，爆轰波随着链分支反应模型中跃变温度的变化，具有不同的传播特性。跃变温度控制着化学反应速度，跃变温度越高，化学反应速度越快。因此可以说化学反应速度越快，爆轰波就越不稳定，这和采用单步反应模型以及基元反应模型得到的结论是定性一致的。

图1 爆轰波传播过程中前导激波后方的压力变化，模型跃变温度0.88，0.90和0.92Fig.1 Post－shock pressure of the detonation with the cross－over temperature 0.88，0.90and 0.92

由于一维爆轰波是一种理想化的激波和燃烧耦合模型，和实际的具有多维胞格结构的爆轰波有所不同，因此进行直接实验对比是非常困难的。对计算得到的爆轰波传播速度和CJ理论的结果进行比较是一种可行的方法，通过对比发现数值结果和理论结果确实是一致的。但是这种对比只是宏观参数的比较过于简单。Short等［13］在提出的三步链锁反应模型时，曾经对一维爆轰波的非线性不稳定性进行了理论和数值研究。由于采用了不同的模型参数，其结果不能直接和本文的结果进行对比，但是爆轰波不稳定性的发展趋势是一致的。Ng等［14］利用采用了相同的模型和参数模拟了爆轰波形成和传播过程，图1显示的爆轰波的脉冲传播过程和其论文中相应的结果是基本相同的，另外对不同参数下的起爆能量进行研究，发现该模型的数值模拟结果和理论结果基本是一致的，从而验证了数值模型的可靠性。

2.2 爆轰波传播过程中的平均能量关系

由于对应不同的化学动力学尺度，爆轰波会形成不同的振荡周期，因此考察每个周期内爆轰波的能量释放规律有助于理解爆轰波的传播机理。对能量方程（4）进行变换可以得到：

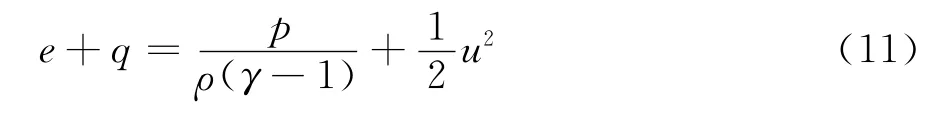
其中x1表示前导激波所在的位置，x0表示波后积分区域的左边界，一般取x0＝0，Δx表示爆轰波移动的距离。对于图1所示的三种不同稳定性的爆轰波，在排除初始不规则传播阶段后（即从“A”，“B”，“C”点往后），其单位传播单位距离内的能量释放如表1所示。计算结果发现对于不同的跃变温度，在任意一个周期内，爆轰波后的总能量、内能和动能的变化基本相同，这也解释了为什么不同稳定性的爆轰波都能够用CJ爆轰理论进行速度计算。然而，对能量释放进行分拆的结果发现，对于不同稳定性的爆轰波，其燃烧能量分配给内能和动能的比例也是相同的。这说明波后能量的分配仅仅取决于气体动力学参数，而和爆轰波的稳定性以及化学动力学参数没有关系。

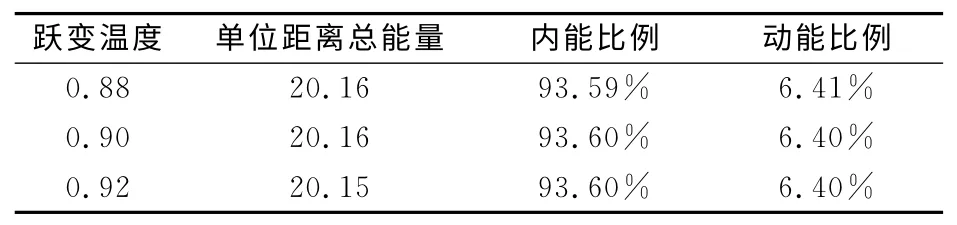
表1 不同跃变温度下，爆轰波后的能量释放和分配规律Table 1 Energy release and distribution laws with different cross－over temperatures

然而，不稳定的爆轰波具有较大的振幅，说明前导激波的马赫数变化较大，而这必然引起波后的内能和动能分配的差异。为了研究振荡周期对于能量释放的影响，表2进一步给出了0.92情况下，在不同的半周期内的能量分配情况。周期的起始点为两个压力极大值中较小的一个，如图1中的“C”点所示，并对模拟得到的三个周期进行了平均。可以看出对于这种双模态振荡的爆轰波，在一个周期内的能量分配有了一定的差异。从较小的极值点到较大的极值点的周期中，不仅爆轰波的波长更长，而且单位距离释放的能量也更多。这个过程对应的内能分配比例减小，动能分配比例增加，从而才能实现从较小极值点到较大极值点的过渡。而这种过渡过程导致总的能量释放和分配比例都偏离了平均值，进而需要在接下来的半个周期中进行补偿。因此，从能量释放的角度，不稳定的爆轰波和稳定的爆轰波不同之处在于，内能分配和动能分配在总量一定的情况下存在相位差，从而导致爆轰波的不稳定性。为此，需要对爆轰波传播过程中，内能和动能分配的相位差关系进行研究。

表2 跃变温度0.92时的周期长度和能量分配Table 2 The oscillation length and energy distribution with the cross－over temperatures 0.92

2.3 爆轰波和能量释放之间的相位差关系

图2和图3分别显示了跃变温度0.90的情况下，爆轰波传播过程中的波后区域的内能和动能增加情况。可以看到内能变化的极大值点略微领先于爆轰波压力的极大值点，但是两者基本上是同步的；而动能的变化极大值点粗略对应于爆轰波压力的极小值点。因此，爆轰波后的化学反应能量释放的分配取决于爆轰波所在的阶段：在爆轰波从波峰到波谷的运动过程中，随着波后压力的降低，波后能量分配给内能的部分逐渐降低，而分配给动能的部分逐渐增加；在爆轰波从波谷到波峰的运动过程中，分配给内能的部分逐渐降低，而分配给动能的部分增加。内能和动能之间的这种关系本质上在于爆轰波是通过放热膨胀驱动的。从图2可以看到，内能的变化始终领先于压力的变化，其极大值和极小值点都在压力极大、极小值点前方。在爆轰波传播过程中，化学反应释放的能量转化为内能的过程，导致压力升高，进而爆轰波加速；然而与此同时，分配给动能的部分越来越少，因此会导致爆轰波减速。同样，化学能转化为动能的过程中，爆轰波加速，但是分配给内能的部分减少导致压力降低，降低了爆轰波速度。内能和动能这两个因素互相制约，最后导致形成了以固定波长和振幅传播的振荡爆轰波。

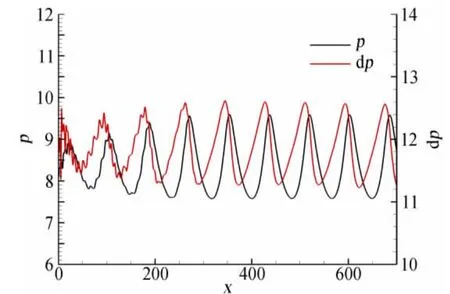
图2 跃变温度0.90的情况下，爆轰波传播过程中的波后区域的内能变化Fig.2 Post－shock internal energy release of the detonation with the cross－over temperature 0.90

图3 跃变温度0.90的情况下，爆轰波传播过程中的波后区域的动能变化Fig.3 Post－shock kinetic energy release of the detonation with the cross－over temperature 0.90

图4 和图5 分别显示了跃变温度0.92 的情况下，爆轰波传播过程中的波后区域的内能和动能增加情况。可以看出内能的增加和爆轰波马赫数的变化是同相的，而动能的增加是反相的，这和跃变温度0.90的结果是一致的。然而，在跃变温度0.92的情况下，能量分配的波动更加剧烈，尤其是动能分配，其波动区间为（0.49：0.96），如图5右轴所示。而跃变温度0.90情况下波动区间为（0.68：0.90），如图3右轴所示。因此，跃变温度0.92对应的内能波动幅度是跃变温度0.90对应波动幅度的2.14倍。然而，对爆轰波稳定性影响更大的是能量分配和爆轰波本身的相位差。表3显示了以爆轰波压力极大值点为基准的内能、动能释放的相位差，其中0.92情况下的第一个数据对应于较小的极大值点而第二个数据对应于较大的极大值点。可以看到总体来说内能的相位差小于动能的相位差，这说明爆轰波传播主要是通过放热导致气体膨胀驱动的。

图4 跃变温度0.92的情况下，爆轰波传播过程中的波后区域的内能变化Fig.4 Post－shock internal energy release of the detonation with the cross－over temperature 0.92

图5 跃变温度0.92的情况下，爆轰波传播过程中的波后区域的动能变化Fig.5 Post－shock kinetic energy release of the detonation with the cross－over temperature 0.92

表3 不同跃变温度下，内能和动能释放的相位差Table 3 Phase difference of the energy release with different cross－over temperatures

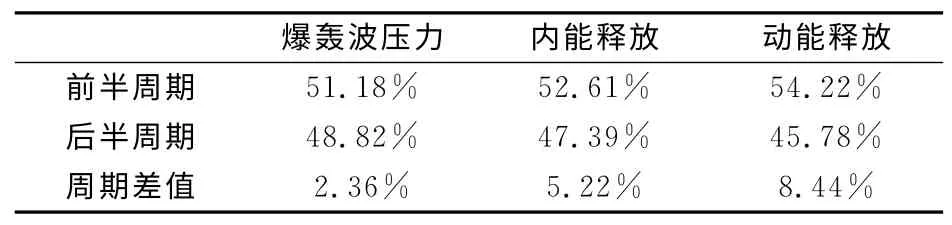
表4 跃变温度0.92情况下，以不同参数衡量的波长周期比例Table 4 The oscillation length derived from different parameters with the cross－over temperature 0.92

然而，对比三个跃变温度的相位差，可见其并不是单调变化的。在跃变温度0.88情况下稳定传播的爆轰波相位差较小，0.90情况下脉动传播的爆轰波相位差变大，而0.92情况下爆轰波的相位差没有继续增加反而变小。从0.88到0.90相位差增加是容易理解的，因为正是由于内能和动能的释放和爆轰波具有较大的相位差，才导致了脉冲爆轰波的存在。但是从0.90到0.92，爆轰波变得更不加稳定了，为什么两个相位差反而减小了呢？这是因为0.92情况下爆轰波化学动力学尺度更长，因此振荡传播的时候波长也更长。如果同时能量分配的相位差增大，就会导致激波和后方的化学反应不能耦合起来，从而导致爆轰波的熄灭。在跃变温度0.92的情况下，爆轰波通过自我调节在一个波长周期内形成了两个不同的波动过程，从而解决了波长增加和相位差增加之间的矛盾。爆轰波这种对波长的自我调节作用，采用其它变量为周期衡量参数时更加明显。表4给出了以不同参数衡量的波长周期比例，第一行表示从较小的极值点到较大的极值点运动的半周期，第二行表示从较大的极值点到较小的极值点运动的半周期。可以看到，虽然以爆轰波压力、内能释放和动能释放三个参数衡量周期长度都相同，但是它们在前半个周期和后半个周期的分配是不同的。以爆轰波压力衡量，两个半周期之间的差距是2.36%，但是以内能释放和动能释放周期衡量，两个半周期的差距分别是5.22%和8.44%。这说明能量释放的相位差是导致爆轰波双模振荡的原因。

3 结论

本文以化学反应模型跃变温度为参数，从能量释放规律的角度研究了爆轰波的传播机理。数值模拟结果显示，对于不同的跃变温度0.88，0.90和0.92，分别会形成稳定传播、单模态振荡和双模态振荡的爆轰波，然而在单位距离的能量释放及其在内能、动能之间的分配比例是不变的。前导激波和波后燃烧之间存在一定的相位差，由此导致了具有较大相位差的爆轰波振荡传播。双模态振荡爆轰波的形成是爆轰物理一个重要的研究内容，以前的研究者曾经采用混沌理论对其进行了数学解释［10］，而本文从激波和燃烧的耦合角度，采用相位差对这个问题进行了物理分析。结果表明其根源在于不稳定爆轰波传播时，较长的波长和较大的相位差产生了矛盾，由此爆轰波自动分解成两种振荡模态。这样能够使前导激波和能量释放之间的相位差减小，从而避免爆轰波的熄灭，同时也形成了更不稳定的双模态振荡爆轰波。

［1］FICKET W，DAVIS W C.Detonation［M］.Berkeley，CA：University of California Press，1979.

［2］WHITE D R.Turbulent structure in gaseous detonations［J］.Phys.Fluids，1961，4：465－480.

［3］KANESHIGE K，SHEPHERD J E.Detonation database［R］.Explosion Dynamics Laboratory Report FM97－8.California Institute of Technology，Pasadena，CA，1999.

［4］GAMEZO V N，DESBORDES D，ORAN E S.Twodimensional reactive flow dynamics in cellular detonation waves［J］.ShockWaves，1999，9：11－17.

［5］GAMEZO V N，DESBORDES D，ORAN E S.Formation and evolution of two－dimensional cellular detonations［J］.CombustionandFlame，1999，116：154－165.

［6］WANG A F，ZHAO W，JIANG Z.The criterion of the existence or inexistence of transverse shock wave atwedge supported oblique detonation wave［J］.Acta Mech.Sin.，2010，30（4）：349－354.

［7］董刚，范宝春，李鸿志.圆锥激波诱导的爆燃和爆轰不稳定性研究［J］.兵工学报，2010，31（4）：401－408.

［8］ERPENBECK J J.Nonlinear theory of two－dimensional detonations［J］.Phys.Fluids，1970，13：2007－2026.

［9］HE L，LEE J H S.The dynamical limit of one－dimensional detonations［J］.Phys.Fluids，1995，7：1151－1158.

［10］NG H D，RADULESCU M I，HIGGINS A J，et al.Numerical investigation of the instability for onedimensional Chapman－Jouguet detonations with chainbranching kinetics［J］.CombustionTheoryandModelling，2005，9：385－401.

［11］WATT S D，SHARPE G J.Linear and nonlinear dynamics of cylindrically and spherically expanding detonation waves［J］.J.FluidMech.，2005，522：329－356.

［12］洪滔，秦承森.一维爆轰波不稳定性的数值模拟［J］.高压物理学报，2003，17（4）：255－260.

［13］SHORT M，QUIRK J J.On the nonlinear stability and detonability limit of a detonation wave for a model threestep chain－branching reaction［J］.J.FluidMech.，1997，339：89－119.

［14］NG H D，LEE J H S.Direct initiation of detonation with a multi－step reaction scheme［J］.J.FluidMech.，2003，476：179－211.

［15］TORO E F.Riemann solvers and numerical methods for fluid dynamics（Second ed.）［M］.Berlin：Springer，1999.