内埋弹舱舱门气动特性研究

吴继飞，徐来武，范召林，唐淋伟

（1.中国空气动力研究与发展中心，四川 绵阳 621000；2.空气动力学国家重点实验室，四川 绵阳 621000）

0 引言

为了满足隐身和超声速巡航的需要，新一代战斗机大都采用内埋式武器装载方式，但武器内埋式装载也引发了许多复杂的空气动力学问题。当要求进行武器发射时，内埋武器系统需要完成舱门迅速开启、武器出舱与分离投放、发射装置收回、舱门快速关闭等动作，而上述动作将对周围流场产生强烈干扰，流动的非定常效应将更加凸显。新一代战斗机设计要求在整个飞行包线范围和临界载荷条件下，武器内埋系统结构完整、机／弹相容；当进行武器发射时，舱门及其控制与驱动系统、武器悬挂与弹射系统能按设计要求正常工作，武器能稳定出舱并能保持预定设计姿态和分离运动轨迹，以有效保证武器打击精度。国内外关于内埋弹舱方面的研究文献很多，但研究模型多为无舱门的方形弹舱（空腔），研究内容主要集中在三方面：弹舱流场绕流特性研究［1］；弹舱流场气动声学特性研究［2］；弹舱流场主／被动流动控制方法研究［3］。少量文献介绍了内埋武器的分离特性［4－5］，而关于舱门气动特性的研究文献则更少［6］。事实上，开展内埋弹舱舱门气动特性方面的研究至关重要，该方面研究不仅可为弹舱舱门设计提供理论依据，同时还可为非定常复杂流动机理研究提供技术支撑。本文以高速风洞试验为手段，对内埋弹舱舱门的气动声学特性、静／动态气动载荷特性进行了较全面的研究，文中给了M＝0.6时双侧舱门保持相同开启角度的静态试验结果以及双侧舱门同步运动的动态试验结果。

1 试验设备及方法

1.1 风洞

本研究在中国空气动力研究与发展中心高速所的FL－23风洞中完成，FL－23风洞为半回流暂冲式亚、跨、超三声速风洞。该风洞试验段入口尺寸为0.6m×0.6m，试验段长度为2.5m，跨声速时上下壁是60°斜孔壁，模型区开闭比为4.3%，加速区开闭比为4.4%，左右为实壁，超声速时四壁均为实壁。试验段左右壁上各有一个尺寸为1.014m×0.54m 矩形堵块，视试验需要，该矩形块可整体取下，为特种试验提供安装平台。本研究即利用了该矩形块拆下的空间作为模型安装平台。马赫数为0.6时对应的来流速度V∞和雷诺数Re分别为197m／s和1.25×107／m。

1.2 研究模型

研究模型由基座、弹舱底板、圆盘、前后整流板、传动齿轮组等部分组成，其装配图如图1。所模拟的弹舱为双舱构型，弹舱中间有一隔板将弹舱分成完全相同的两部分，弹舱长度L为325mm，单侧弹舱宽度W为70.5mm，深度D为50mm，即弹舱长深比L／D为6.5。舱门简化成平板模型，厚度为6mm，靠近风洞下洞壁的一扇舱门上布置有42个动态压力测点，内外表面各21个，对称分布。模型安装于风洞中的图片如图2。定义弹舱前缘中心处为坐标原点，x轴指向弹舱后壁，z轴指向舱门门轴，文中以X／L表示测点的沿x轴的相对位置，以Z／W表示测点的沿z轴的相对位置。

图1 试验模型装配图Fig.1 Assembly drawing of testing model

图2 试验模型照片Fig.2 Sketch of testing models

1.3 电机驱动及控制系统

电机型号为松下MDMA15ZP1D，驱动器型号为松下MDDDT5505。每扇舱门由一台电机控制，电机安装在模型基座上，位于弹舱后缘（如图1），通过多级齿轮传动将电机的旋转运动转变为舱门开闭运动。控制系统选用松下MINAS－A4系列高性能交流伺服驱动系统，速度响应频率为1kHz。控制系统选用研华PCI－1240 运动控制卡，控制系统软件是在Windows XP操作系统下，通过LabWindows／CVI 9.0设计开发的，可实现舱门速度调节、开闭方式转变、舱门开启角度设置、电机抱闸等功能。

1.4 测试设备

舱门开启角度采用标准轴型单圈绝对编码器测量，其分辨率达到13 位，即对角度测量精度为360°／213≈0.044°。舱门上所使用的动态压力传感器是由美国Kulite公司生产的LE－062型绝对式传感器，其量程为10PSI，固有频率为175kHz，名义灵敏度为1.45×10－3mV／Pa。动态压力数据采用奥地利DEWETRON 公司基于PCI总线的数据采集系统，该系统主要由DEWE－ORION－1624采集模块组成，编码器信号与动态压力传感器信号同步采集，确保其在时间上保持一致性。

1.5 数据处理方法

对于静态试验，测点压力不存在“瞬时”规律性，但具有“统计”规律性，可以用概率论和统计方法从幅值域和频率域来描述脉动压力特性，本文采用FFT变换方法进行分析。集中载荷处理方法如下：静态试验时，将舱门固定某一开度时的测量结果进行平均得测点静压，舱门内、外表面对应测点的静压相减得到该点的压力差，以测点位置为中心对舱门进行网格划分，面元内压力用其中心位置的压力代替，压力乘以面元面积即为各面元处的法向力，门轴中心为参考点，坐标系采用右手系，进行处理后即可得到舱门的气动力（矩），以单侧舱门面积为参考面积；动态试验时，将舱门内、外对应测点相同时刻的压力值相减，并采用静态试验时类似的气动力计算方法，得到动态气动力（矩）结果，再通过多点平均获得较平滑的动态气动力（矩）曲线，无量纲化时采用的参考面积与静态试验相同。

2 试验结果分析

2.1 静态试验结果分析

图3给了舱门开启角度δ＝90°时，舱门内、外表面测点总声压级（OSPL）分布情况，为了便于比较，图中同时给出了弹舱底部的总声压级分布。图中表明：X／L＞0.2以后，舱门内外表面多数区域都属于附着流，舱门内、外表面纵向声压级分布波动量明显小于舱底声压级分布的波动量；Z／W＝0.57、0.86时舱门前缘附近气流分离较严重，气动噪声较强，其峰值与舱底最大声压级相当；总体来说，相同Z／W下，舱门内侧测点的总声压级要大于舱门外侧对应测点，离舱门门轴越近气动噪声越强，这表明舱内气动噪声在舱门表面附近依然有一定影响，但随Z／W增大，该影响明显减弱。

图4 给出了舱门前、后缘附近（X／L＝0.07、0.93）测点的声压谱特性曲线，图中同时给出了相近纵向位置舱内测点的声压谱曲线。图中表明，X／L＝0.07时，舱门内外表面测点声压谱曲线分布特性与舱内测点（X／L＝0.05）不同，舱门测点能量分布频域较宽，能量随频率增大衰减较慢，而舱内测点能量则集中在f＝0～2.5kHz范围内，且随频率增大能量衰减较快，另外，舱门内侧测点声压谱曲线上存在能量尖峰，其频率与舱内测点声压谱曲线上能量尖峰的对应频率一致，这表明弹舱流场引发的自持振荡同样会对舱门周围的流场产生影响，因此在舱门结构设计和疲劳载荷计算时必须认真考虑该问题；X／L＝0.93时，舱门内外表面测点声压谱曲线分布特性与舱内测点（X／L＝0.93）相似，舱门内侧测点声压谱曲线上同样存在有能量尖峰。

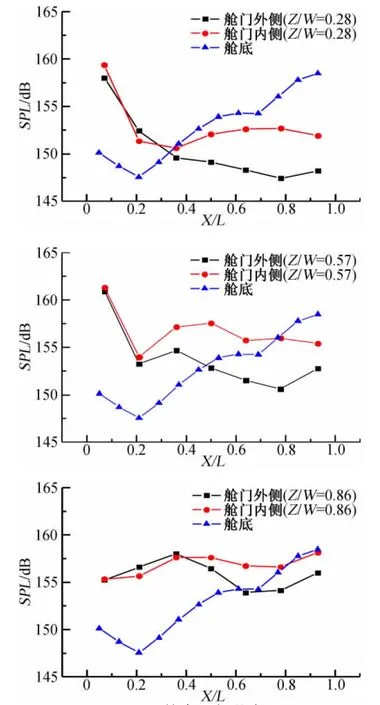
图3 总声压级分布Fig.3 Distributions of overall sound pressure level

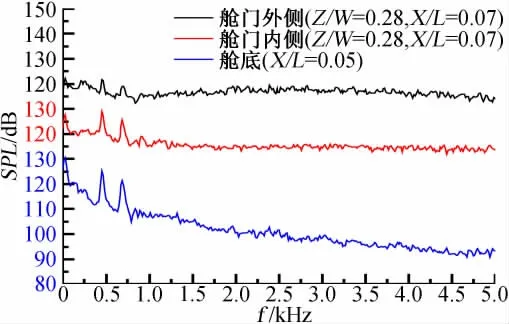
图4 声压谱曲线Fig.4 Distributions of sound pressure spectra

图5给出了舱门法向力系数随舱门开启角度变化曲线，图中表明，β＝0°时，CN随δ增大先急剧增大后逐渐减小，造成这种现象的原因可能是：较小开启角度下，舱门对气流有堵塞作用，大部分气流将绕过舱门前缘向后流动，舱门外侧气流加速，压力较低，而此时从舱门内侧上方流经弹舱的气流较少，加之弹舱对其附近的气流产生减缓作用，因此舱门内表面附近气流速度相对较低，压力较高，舱门内外表面的压力差产生了有利于舱门开启的气动力，且在某一舱门开度下，该气动力达到最大值，之后随δ增大，从舱门内侧上方流经弹舱的气流增多，且舱门受弹舱流场干扰开始减弱，舱门内外压力差逐渐减小，作用于舱门的气动力也随之降低。图中还表明，与β＝0°相比，β＝3°时，有利于舱门开启的气动力更明显，δ＝30°～90°时，舱门气动力变化不明显。造成这种现象的原因是：该试验条件下，β＞0°时，测试舱门内侧为迎风面，内侧迎风作用产生有利于舱门开启的气动力，且δ＝90°时来流在舱门法向上的速度分量最大，因此，与β＝0°的试验结果相比，该舱门开度下的气动力增量最大。图中还给出了β＝－3°时的试验结果，与β＝0°相比，该侧滑角下的气动力明显减小，且减小量与β＝3°时的增量相当。

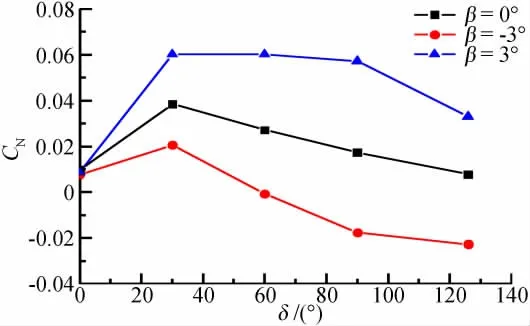
图5 舱门法向力系数曲线Fig.5 Normal force coefficient of weapon bay's door

2.2 动态试验结果分析

文中给出了四组St数下舱门开启过程和关闭过程的试验结果。

上式中T为舱门完成一次开启或关闭运动的时间，单位为s。

图6给出了舱门开启过程中的法向力系数，为了便于比较，图中同时给出了静态试验下的结果。图中表明，St数变化对舱门法向力系数影响明显，随St数减小，舱门法向力系数逐渐增大，且其增大的幅度有所减低，St＝0.0028时，动态试验结果与静态试验结果接近，但量值上仍小于静态试验结果。造成上述现象的原因是：相对静态试验，舱门运动产生附加气动载荷，舱门开启时，将产生与舱门运动方向相反的横向流动，该横向流动会产生与舱门运动方向相反的作用力，阻碍舱门的运动，一般来说，该附加气动载荷与舱门运动速度以及来流速压有关，舱门运动速度越快、来流速压越高，该附加气动载荷越大；舱门开启产生的附加气动载荷与静态试验时舱门产生的气动载荷方向相反，故与静态试验相比，舱门开闭过程中的气动载荷偏小，St＝0.0106时，舱门开启过程中最大法向力系数仅为静态试验时最大法向力系数的一半左右。

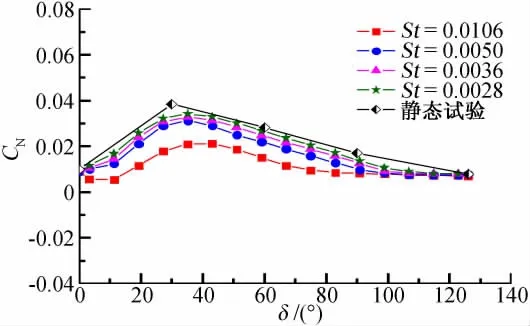
图6 不同St数下的法向力系数Fig.6 Normal force coefficient at different St numbers

图7给出了舱门关闭过程中的法向力系数。图中表明，舱门关闭运动同样可能产生较大的附加气动载荷，由于舱门关闭过程中产生的附加气动载荷方向与静态试验的气动载荷方向相同，因此，理论上舱门关闭过程中的气动载荷比静态试验要大，舱门快速关闭过程中（St＝0.0109）的最大法向力系数约比静态试验时的最大法向力系数高出约20%；舱门关闭运动时，St变化引起的气动载荷变化没有舱门开启过程明显，图中可以看出，St从0.0037减小为0.0028时，舱门气动载荷基本上没有变化，此时，动态试验结果与静态试验结果非常接近，由舱门关闭运动产生的附加气动载荷基本可以忽略。

图7 不同St数下的法向力系数Fig.7 Normal force coefficient at different St numbers

3 结论

通过上述分析，得到以下结论：

（1）舱门前缘气动噪声较强，弹舱流场引发的自持振荡对舱门附近流场依然有影响，因此在进行舱门结构设计和疲劳载荷计算时须充分考虑；

（2）舱门法向力随舱门开启角度变化剧烈，δ≈30°时舱门法向力最大；

（3）舱门开启／关闭过程中的气动载荷随St数变化明显；舱门开启与关闭过程中的气动载荷存在显著差异。

［1］TRACY M B，PLENTOVICH E B.Characterization of cavity flow fields using pressure data obtained in the Langley 0.3－meter transonic cryogenic tunnel［R］.NASA TM 4436，1993.

［2］CHUNG K M.A study of transonic rectangular cavityof varying dimensions［R］.AIAA 99－1909.

［3］CATTAFESTA L，WILLIAMS D，ROWLEY C，etc.Review of active control of flow－induced cavity resonance［R］.AIAA 2003－3567.

［4］STALLINGS R L Jr，FORREST D K.Separation characteristics of internally carried stores at supersonic speeds［R］.NASA TP－2993，1990.

［5］吴继飞，罗新福，范召林.内埋式弹舱流场特性及武器分离特性改进措施［J］.航空学报，2009，30（10）：1840－1845.

［6］史爱明，叶正寅，杨永年.内埋式弹舱舱门气动载荷计算分析研究［J］.航空计算技术，2007，37（3）：5－6.