基于分形理论的鄱阳湖城市群规模结构优化研究

李海鸣

城市群的形成、发展及其带动作用已经成为推动一个国家或地区经济快速发展的主要动力。城市群各城市之间的等级规模结构及其分工是否合理，对城市群中各城市准确定位、相互协调、共同推动城市群的发展乃至带动区域经济发展都有着极其重要的意义。江西提出“龙头昂起，两翼齐飞，苏区振兴，绿色崛起”的发展战略，其“龙头”无疑是指依托于鄱阳湖生态经济区的鄱阳湖城市群。

一、分形理论及其应用

分形理论源自分形几何学，是法国数学家曼得尔布罗特（Mandelbrot）在1973年首次提出的，他把一些部分与整体以某种方式相似的形体称为分形，并创立分形几何学。通常把在分形几何学基础上，形成的研究分形性质及其应用的科学，称为分形理论。分形有两个重要的特征［1］，其一是自相似性。自相似性是基本的分形原理，它表明分形通常在几何变换下具有不变性，即分形构成一个局部和整体自相似体系。其二是分维性。分维是分形的定量表征和基本参数，即描述连续空间的维数。曼得尔布罗特把分形定义为豪斯道夫维数大于或等于拓扑维数的集合。

分形作为与浑沌和耗散结构并列的自然科学的三大发明之一，为非线性系统的研究提供了工具［2］。自其被发现以来，人们借助它对许多领域的非线性问题进行了研究。人们对城市规模分布的研究发现，城市和城市群是典型的自相似体系，它反映城镇空间分布的普遍规律，城市规模分布具有分形特征。其分析模型可表述为：对于某一区域，假设有若干城市分布于其中，由于一般情况下城市和乡镇并没有明确的地理界线，因此，在进行模型分析时，通常按人口多少来度量，以R≧r的聚落为城市，这时，随着r值的改变，区域内城市数量也会改变，如果用N(r)表示区域内城市数目，那么N（r）与r之间呈幂函数关系：

比照豪斯朵夫（Hausdorff）维数公式可知式（1）为一分形模型。其中，r为衡量人口多少的尺度，N（r）为区域内城市数，D为分维数，C为常数。在这一模型中D就可以反映城市规模分布的等级差异。但实际应用中，它有一个缺点：人口尺度的步长对分维值的计算结果有一定干扰［3］。因此，很多研究者利用Zipf维数来研究反映城市规模分布的等级差异。事实上，Zipf公式的一般形式与其等价，其公式可表示为：

这里，x表示城市位序，P（x）表示序列为x的城市规模（人口、经济、功能、面积等），P1是最大城市的规模，q为Zipf指数，在理论上，q=1/D具有分维性质，因此，也把q称之Zipf维数。

由于Zipf公式是经验公式，所以大家对q的意义迷惑不解，直到分形理论出现以后，人们才意识到它的分维数含义［4］：

（1）当D=q=1时，有P1/Pn=n。表明此时区域内的城市规模分布性态良好，同时区域内的城市数恰好等于最大城市与最小城市的人口数目之比。

（2）当D>1即q<1时，表明区域内各城市人口分布比较均匀，城市规模分布比较集中，中小城市比较发展较好，首位城市的垄断性还不强。

（3）当D<1即q>1时，表明区域内各城市人口分布差异较大，城市规模分布分散，首位城市的首位特征明显。

（4）当D→∞即q→0时，所有的城市趋于一样大；当D→0即q→∞时，区域内只有一个城市为绝对的首位型分布。一般来说这两种情况都不会出现。

（5）如果按时间序列观察，当D值减小，q值增大时，城市规模分布趋于分散，说明大城市发展快于中小城市；当D值增大，q值减小时，城市规模分布趋于集中，说明中小城市发展快于大城市时。

二、鄱阳湖城市群等级规模结构分析

（一）鄱阳湖城市群现状分析

鄱阳湖城市群是以鄱阳湖生态经济区规划范围为基准，考虑到数据获取的因素，包括南昌、景德镇、鹰潭、九江、新余、抚州市区及其所辖的部分县市以及宜春、上饶、吉安的部分县、市，共31个县、市。按照《江西省统计年鉴2010》中2009年的人口数据，我们使用非农业人口作为城市规模的特征值，由于在2010年的统计年鉴中，所有设区市的人口不再像以前年度有非农人口的统计，只有年末总人口及全年平均人口。因此，对该年度的社区市人口就一律选用年末市区总人口。这些城市中超过200万人口的超大城市只有南昌市，100万至200万人口之间的特大城市有抚州市1座，50-100万人的大城市有新余、九江2座，20-50万的中等城市有景德镇、丰城、鹰潭等共6座，20万人以下城市有21座（表1）。所有城市非农人口数（按从大到小排序,表2）。

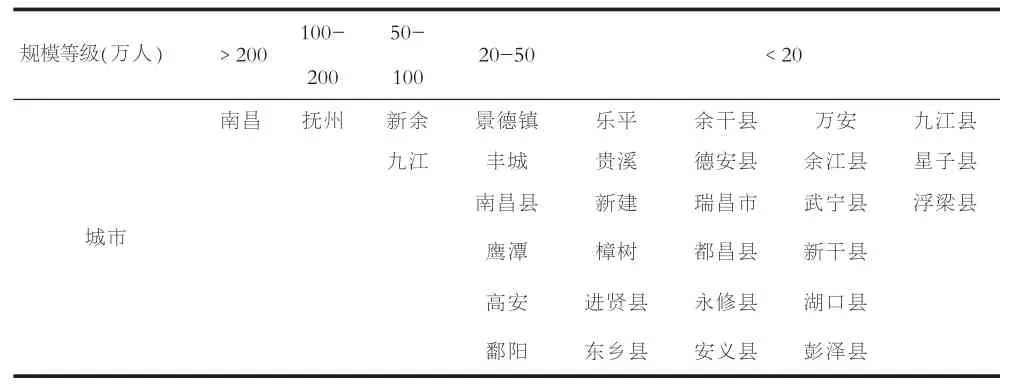
表1 鄱阳湖城市群等级规模

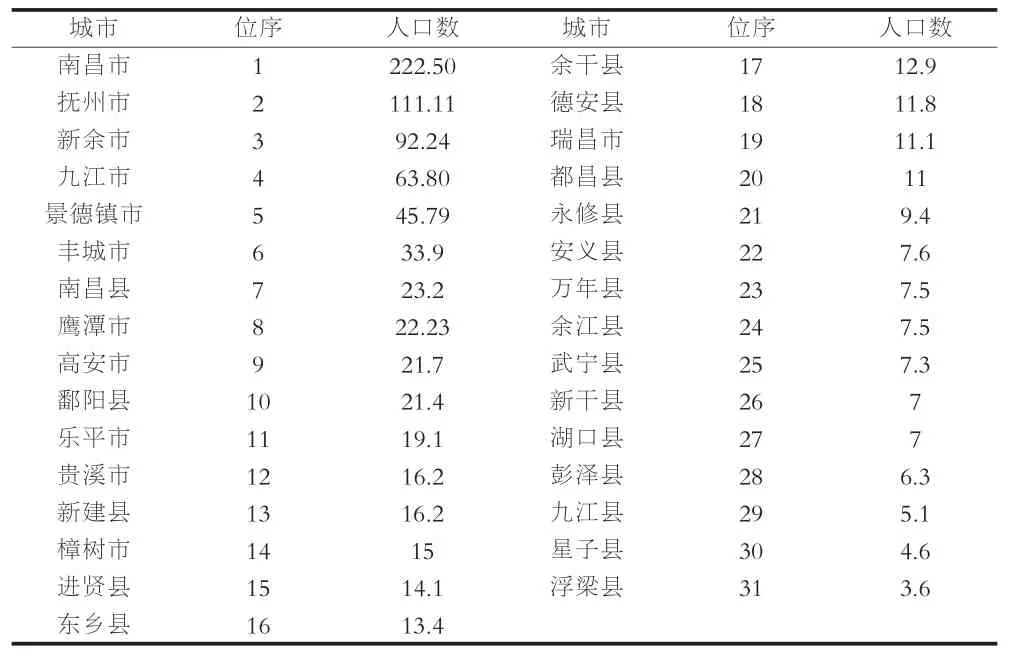
表2 2009年鄱阳湖城市群各城市人口数（万人）

（二）鄱阳湖城市群等级规模结构实证分析

为了能更好地说明鄱阳湖城市群等级规模现状，先借助衡量城市规模分布的城市首位律来考察该区域的城市首位度。分别算出2009年该区域的二城市指数（S2）、四城市指数（S4）及十一城市指数（S11）。

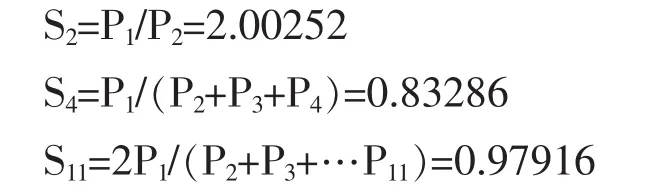
再利用Zipf公式分析鄱阳湖城市群等级规模分形维数。为此，先将（2）式变形为：

令 k=p11/q，D=1 q，则（3）式可写为：

显然该式具有分形意义，分维值为D=1/q。

为能更好地进行回归模拟，我们将（4）式两边取对数，可得：

然后通过Excel软件，进行线性回归模拟，得图1。相关系数R2=0.9778，分维值为1.123。

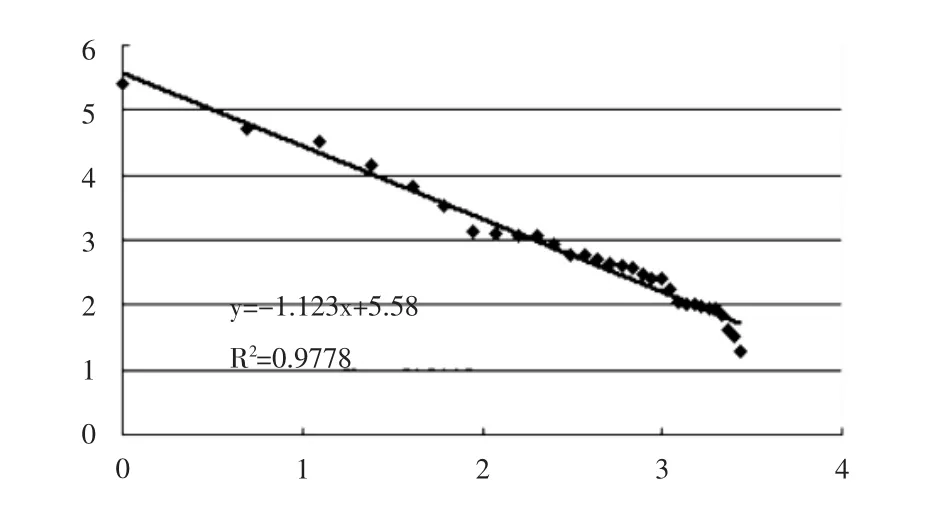
图1 2009年鄱阳湖城市群城市体系位序规模分布双对数散点图

我们用同样的方法，对多年的数据进行处理，得出鄱阳湖城市群规模结构指数的变化情况，为能较全面的进行评价，在进行数据处理时，还引入国内生产总值，计算其分维值的变化。具体结果如表4所示。同时，我们对历年的城市指数也进行了统计（表5）。

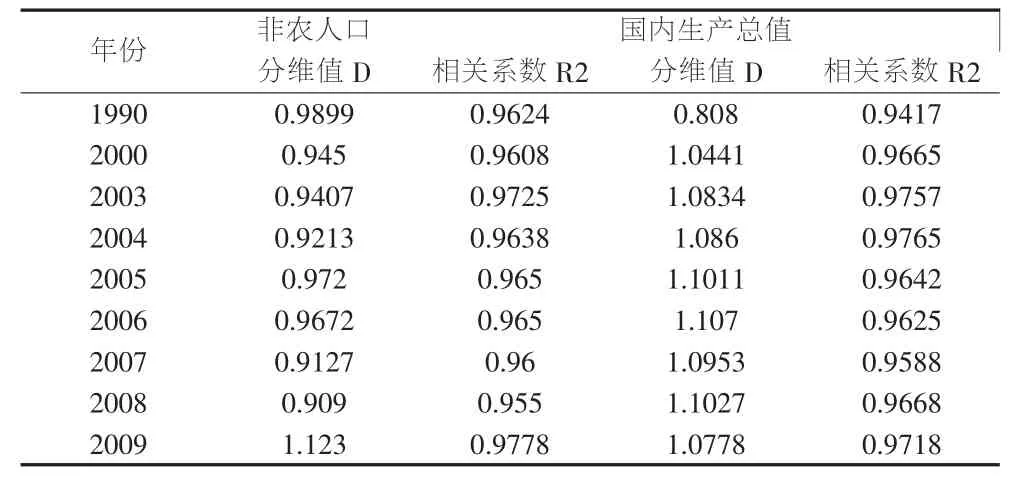
表4 鄱阳湖城市群等级规模分布分维值变化表

（三）实证结果分析

（1）表4显示，每次回归模拟的相关系数R2均在0.95以上，这说明鄱阳湖城市群的城市规模分布具有非常显著的分形特征，城市群自组织能力较强。

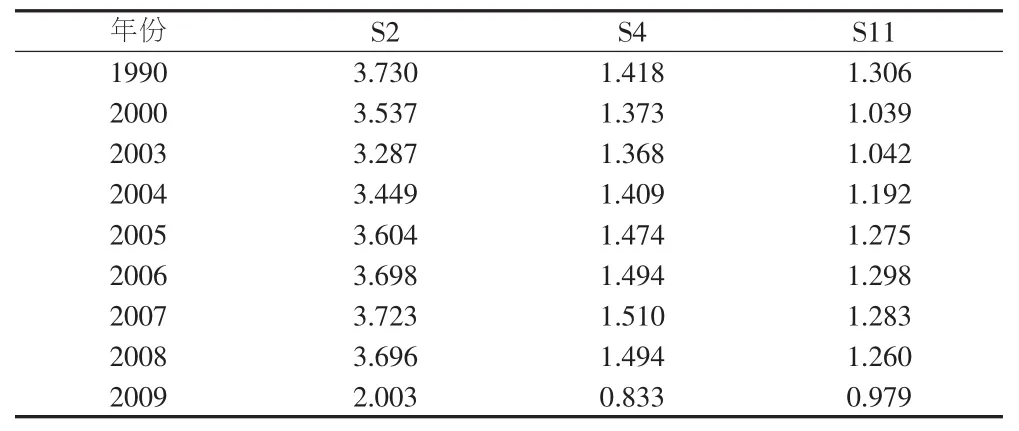
表5 鄱阳湖城市群部分年份城市指数统计

（2）从表1看，2009年鄱阳湖城市群城市规模层次较丰富，但各等级城市分布并不均匀，中间规模等级城市较少，而小城市数量偏多。如果考虑2009年数据中设区市人口为年末总人口而非非农业人口，再参考2008年的非农业人口数据及历年人口增长情况，那么，南昌市区的非农业人口将达不到200万，抚州及新余两市区的非农业人口将达不到50万。这样，小城市数量偏多的情况将会更加突出。

（3）按照位序—规模的原理，二城市指数为2，四城市指数和十一城市指数为1是城市规模结构的理想状态。从表5可以看出，首先，除2009年外，其他历年的二城市指数都在3以上，四城市指数及十一城市指数均大于1。这说明鄱阳湖城市群人口首位分布明显，南昌的人口优势明显。其次，S2指数明显偏大，S11明显小于S4，这说明鄱阳湖城市群单核结构显著，次级中心城市较少，小规模城市较多。再次，S2、S4从1990至2003年，S11从1990至2000年，呈下降趋势；S2、S4从 2003 至 2007 年，S11从 2000 至 2006 年，呈递增趋势。这说明南昌的首位优势从上世纪九十年代到2007至2008年间先降后升。

（4）从表4可以看出，城市群非农人口的分维值均小于1，这表明鄱阳湖城市群体系的人口分布差异较大，城市规模分布分散，首位城市南昌的垄断性较强。再从人口分维值的动态变化来看，总体上分维值呈递减态势，2005、2006两年有反复，这说明在观察年度中，大城市的发展趋势要快于中小城市，即总体上南昌市的非农人口扩较张要快于其他中小城市，2005、2006两年，中小城市的非农人口增长较显著。这与基于城市指数的首位律分析基本吻合。

再看以国内生产总值作为指标来反映的鄱阳湖城市群的经济分布情况。除1990年外，其他年份国内生产总值的分维值均大于1，这说明城市群国内生产总值的分布较均衡，中小城市经济发展较之上世纪90年代初有较大的进步，首位城市南昌的经济影响较上世纪90年代初有较大的下降。从变化趋势上看，分维值呈逐年增大的趋势，但最近年份又趋于下降。可知，中小城市的经济发展要快于南昌市，但最近几年南昌市的经济发展较其他城市有所加快。

三、政策建议

壮大整个城市群的规模。总体上看，无论是人口还是国内生产总值的分维值偏离1都非常小，说明鄱阳湖城市群城市规模分布基本符合位序—规模分布规律。但与其他城市群相比较，我们就会发现，鄱阳湖城市群的规模分布是一种低水平的均衡，在现在区域竞争日益激烈的情况下，如果不壮大整个城市群的规模，将会成为其他区域发挥极化作用的对象，很难在竞争过程中实现进位赶超的政策目标。

进一步突出首位城市南昌的核心地位。从上面的分析可知，在鄱阳湖城市群中，南昌的首位特征比较明显。但必须清醒地认识到，这是基于其他城市人口偏少，城市规模较小的前提下的结果。如果放眼其他引领城市群发展的首位城市来看，不要说不能像上海引领长三角城市群，广州、深圳引领珠三角城市群，北京、天津引领环渤海城市群那样，就是与中部地区的武汉之武汉城市圈，长沙之长株潭城市群，郑州之中原城市群相比，也很难发挥其带动和引领城市群整体经济运行的作用。何况，根据上面的实证分析，南昌在经济总量的指标上，并不像其人口指标那样，首位特征明显，而是发展较之城市群其他中小城市更慢。因此，必须要做大做强中心城市南昌，充分发挥其在城市群乃至全省经济社会发展中重要的战略地位，增强其经济辐射力和凝聚力，使其成为能带领城市群与其他区域进行有效竞争的真正的区域核心。

提升次级中心城市规模，努力形成多元支撑发展格局。鄱阳湖城市群城市规模特征是，如果以市区非农人口来计量城市规模，城市群中将出现50～100万人口的大城市的断档，这将会影响到不同等级城市自身功能的发挥。因此，可以对九江、新余、抚州、景德镇等城市给予政策扶持，加快这些城市的人口及产业集聚，使他们成为城市群中联系首位城市和中小城市的纽带，促进整个城市群协调均衡地发展。

大力发展中小城镇，使它们成为带动地方发展的增长极。对一些发展潜力大，竞争优势明显的小城市，应进一步加大投资，使它们能较快地发展成为中等城市，从而避免分维值的减小，逐步提升城市群的层级，如乐平、贵溪、新建、樟树等市县。对于人口规模较小的城镇，要努力其挖掘自身优势，合理引导人口集聚，积极承接中等城市的辐射带动，加快城镇化进程，以增强城市群综合经济实力。

[1][2]邝敏毅.基于分形理论的广东省城市群落实证研究[D].华南理工大学硕士学位论文.2006

[3]夏永久.基于分形理论的皖江城市带城镇体系结构研究[J].资源开发与市场，2009（1）.

[4]林鸿溢，李映雪.分形论—奇异性探索[M].北京：北京理工大学出版社，1992.