矩阵特征值求解及其在图像压缩中的应用

马志勇，方 珑

(上海第二工业大学理学院，上海201209)

矩阵特征值求解及其在图像压缩中的应用

马志勇，方 珑

(上海第二工业大学理学院，上海201209)

在简单阐述了矩阵特征值的数值求解理论之后，介绍了几种常用的求解矩阵特征值的方法，并最终将特征值计算应用到图像压缩中。

特征值数值算法；矩阵压缩；图像处理

0 引言

矩阵的特征值计算虽然有比较可靠的理论方法，但是，理论方法只适合于矩阵规模很小或者只是在理论证明中起作用，而实际问题的数据规模都比较大，不太可能采用常规的理论解法。计算机擅长处理大量的数值计算，所以通过适当的数值计算理论[1-3]，写成程序，让计算机处理，是一种处理大规模矩阵的方法，而且是一种好的方法。常用的特征值数值方法包括幂法、反幂法、雅克比方法、QR分解法等。其中，幂法适用于求解矩阵绝对值最大的特征值，反幂法适合求解矩阵的逆矩阵的特征值，雅克比方法适合求解对称矩阵的特征值，QR分解法主要使用于求中小型矩阵以及对称矩阵的全部特征值。

矩阵乘以一个向量的结果仍是同维数的一个向量。因此，矩阵乘法对应了一个变换，把一个向量变成同维数的另一个向量，变换的效果当然与方阵的构造有密切关系。比如，可以取适当的二维方阵，使得这个变换的效果就是将平面上的二维向量逆时针旋转30度，这时我们可以问一个问题，有没有向量在这个变换下不改变方向呢？可以想一下，除了零向量，没有其他向量可以在平面上旋转30度而不改变方向，所以这个变换对应的矩阵（或者说这个变换自身）没有特征向量（注意：特征向量不能是零向量），所以一个特定的变换特征向量是这样一种向量，它经过这种特定的变换后保持方向不变，只是进行长度上的伸缩而已。矩阵论在图像中的应用比如选取特征值最高的k个特征向量来表示一个矩阵，从而达到降维分析-特征显示的方法。一般而言，这一方法的目的是将原始数据集合变换到主分量空间，使单一数据样本的互相关性降低到最低点。图像压缩处理就是通过矩阵理论减少表示数字图像时需要的数据量，从而达到有效压缩。

1 特征值求解的数值方法

我们首先介绍几种常用的求解特征值的数值方法。

（1）幂法。幂法就是求矩阵的绝对值最大的特征值和相应特征向量的方法。

如果1λ是矩阵A的特征值，并且其绝对值比A的任何其他特征值的绝对值大，则称它为主特征值。相应于主特征值1λ的特征向量1V称为主特征向量。如果特征向量V中绝对值最大的分量为1，则称其是归一化的。

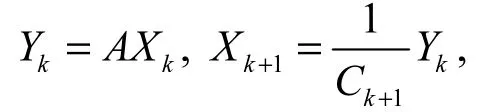
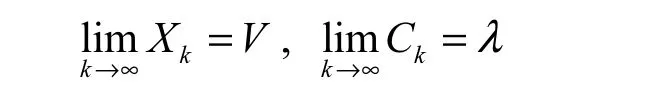
注：如果0X是一个特征向量且0XV≠, 则必须选择其他初始向量。

（2）反幂法。反幂法可以用来计算矩阵绝对值最小的特征值及其对应的特征向量。

设A是n阶非奇异矩阵，有n个线性无关的特征向量X1,X2,…,Xn, 它们对应于特征值λ1, λ2,…,λn, 满足不等式，其中AXi=λiXi( i=1,2,…,n)。因为A非奇异，所以λi≠0, 由AXi=λiXi得A−1Xi=Xi/λi。

所以A−1的特征值是A的特征值的倒数。计算A的绝对值最小的特征值λn的问题就是计算A−1绝对值最大的特征值1/λn的问题，于是可用幂法求出A−1的绝对值最大的特征值，即A的绝对值最小的特征值。计算方法如下。

其中0V为初始向量。

（3）雅克比方法。雅克比方法的基本思想是通过一系列的由平面旋转矩阵构成的正交变换将实对称矩阵逐步化为对角阵，从而得到全部特征值及其相应的特征向量。

2 矩阵的特征值求解在图像压缩中的应用

利用矩阵分解以及矩阵特征值的求解方法，可以将其应用到很多方面[4-5]，例如矩阵压缩、马尔科夫过程、天气预报等等，我们这里简单介绍其在图像压缩方面的应用。矩阵的压缩是指利用矩阵的分解之后，提取特征值较大的特征值，舍弃比较小的特征值。还是因为在矩阵理论中，特征值代表了信息量，所以保留比较大的特征值、舍弃比较小的特征值，可以达到矩阵压缩的目的。而图像压缩由于使用特征值分解压缩图片存在着不可靠性，所以采用一种新的矩阵分解方法来提取数字图像的特征信息，那就是矩阵的奇异值分解。奇异值分解非常有用，对于矩阵Am×n, 存在Um×n, Vm×n, Sm×n, 满足A=U×S×V 。U和V中分别是A的奇异向量，而S是A的奇异值。AA'的正交单位特征向量组成U，特征值组成S'S，A'A的正交单位特征向量组成V, 特征值（与AA'相同）组成SS'。因此，奇异值分解和特征值问题紧密联系。

把获得的奇异值，取其中比较大的（类同特征值的提取压缩方法）奇异值，然后使用同样的方法，进行压缩，其本质其实还是使用类似矩阵分解，然后提取特征的方法，让比较小的奇异值舍去，以达到数字图像压缩的目的。

使用普通相机拍摄的图像A(见图1)，大小为256×256。

图1 使用普通相机拍摄的图像AFig. 1 Using an ordinary camera, the image A

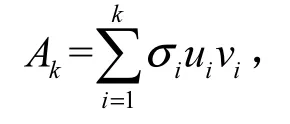
以下是不同压缩比例的图像。

提取500个奇异值后的压缩图像如图2；提取300个奇异值后的压缩图像如图3；提取100个奇异值后的压缩图像如图4，图像比较模糊，说明奇异值个数不可以取得过少。

图2 提取500个奇异值后的压缩图像Fig. 2 The compressed image after extraction 500 singular value

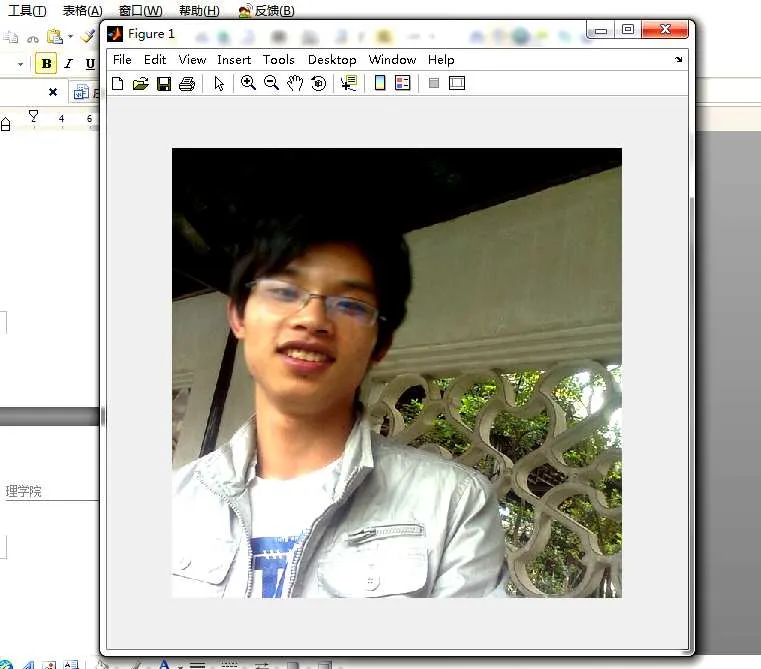
图3 提取300个奇异值后的压缩图像Fig. 3 The compressed image after extraction 300 singular value

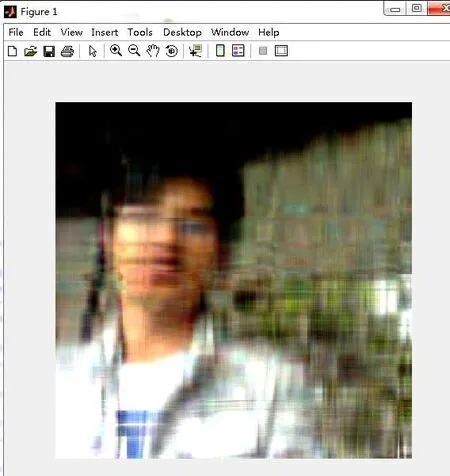
图4 提取100个奇异值后的压缩图像Fig. 4 The compressed image after extraction 100 singular value

3 图像压缩效果的评估

经典的视频压缩算法已渐形成一系列的国际标准体系，如H.26x系列建议、H.320系列建议以及MPEG系列建议等。压缩方法的质量经常使用峰值信噪比来衡量，峰值信噪比则用来表示图像有损压缩带来的噪声。但是，观察者的主观判断也被认为是一个重要的、或许是最重要的衡量标准。

特征值的应用不仅仅在于图像处理上，在物理、材料、力学等方面都有各种应用。有人曾在书里这样说过“有振动的地方就有特征值和特征向量”，以后我们将进一步探讨矩阵理论及其相关应用。

4 图像压缩的相关步骤

clear,clc

infile='C:psu4.jpg';

A=imread(infile); % 读取图像

A(:,:,1)

imshow(A);xlabel('原始图像');

A=double(A); % 数据格式转换

A(:,:,1);

[U1 S1 V1]=svd(A(:,:,1));

[U2 S2 V2]=svd(A(:,:,2));

[U3 S3 V3]=svd(A(:,:,3));

U1*S1*V1';

A(:,:,1)-U1(:,1:500)*S1(1:500,1:500)*V1(:,1:500)';

W(:,:,1)=U1(:,1:500)*S1(1:500,1:500)*V1(:,1:500)';

W(:,:,2)=U2(:,1:500)*S2(1:500,1:500)*V2(:,1:500)';

W(:,:,3)=U3(:,1:500)*S3(1:500,1:500)*V3(:,1:500)';

imshow(uint8(W))

pause

A(:,:,1)-U1(:,1:300)*S1(1:300,1:300)*V1(:,1:300)';

W(:,:,1)=U1(:,1:300)*S1(1:300,1:300)*V1(:,1:300)';

W(:,:,2)=U2(:,1:300)*S2(1:300,1:300)*V2(:,1:300)';

W(:,:,3)=U3(:,1:300)*S3(1:300,1:300)*V3(:,1:300)';

imshow(uint8(W))

pause

A(:,:,1)-U1(:,1:10)*S1(1:10,1:10)*V1(:,1:10)';

W(:,:,1)=U1(:,1:10)*S1(1:10,1:10)*V1(:,1:10)';

W(:,:,2)=U2(:,1:10)*S2(1:10,1:10)*V2(:,1:10)';

W(:,:,3)=U3(:,1:10)*S3(1:10,1:10)*V3(:,1:10)';

imshow(uint8(W))

[1] MATHEWS J H, FINK K D, 著. 周璐, 陈渝, 钱方, 等译. 数值方法(MATLAB版)[M]. 第四版. 北京: 电子工业出版社, 2005.

[2] 林成森. 数值分析[M]. 北京: 科学出版社, 2006.

[3] 奚梅成, 刘儒勋. 数值分析方法[M]. 合肥: 中国科学技术大学出版社, 2003.

[4] 张汗灵. Matlab在图像处理中的应用[M]. 北京: 清华大学出版社, 2008.

[5] 张贤达. 矩阵分析与应用[M]. 北京: 清华大学出版社, 2004.

Matrix Eigenvalue and Its Application in Image Compression

MA Zhi-yong, FANG Long
( School of Science, Shanghai Second Polytechnic University, Shanghai 201209, P. R. China )

The theory of the numerical solution of the matrix decomposition and eigenvalue was briefly discussed. And then, several special matrix eigenvalue solution methods was introducted which was commonly used. Finally, image compression reached a new height of matrix decomposition and application of the corresponding eigenvalue.

eigenvalue numerical algorithms; matrix compression; image compression

O29

A

1001-4543(2012)04-0315-04

2012-09-15;

2012-10-09

马志勇（1980－），男，河南人，讲师，博士，主要研究方向为偏微分方程及其动力系统，电子邮箱zyma@sf.sspu.cn。

校重点课程高等代数基金项目（No. A20KC110002）