三次样条插值端点约束条件的构造与Matlab实现
2012-08-16邢丽
邢 丽
(上海第二工业大学理学院,上海201209)
三次样条插值端点约束条件的构造与Matlab实现
邢 丽
(上海第二工业大学理学院,上海201209)
在工程计算中,样条插值技术的研究越来越重要。三次样条插值的边界条件是根据实际问题在端点的状态给出。通过研究三次样条函数插值,针对不同的端点约束,用Matlab计算分析,显示各区间段三次样条函数体表达式,计算出已给点插值并显示各区间分段曲线图,并应用到实际问题中。重点讨论端点约束条件以及混合边界条件。
计算数学;三次样条插值;端点约束;Matlab
0 引言
在工程计算中,插值技术的研究越来越重要。样条插值,就是利用已经测得的一系列的点,在每个节点区间内建立三次多项式函数,通过条件限制,使所得函数曲线或曲面一次、二次导数均存在,即拟合出的曲线或曲面是连续的,并具有较好的光滑性。因此,样条插值函数是实际应用中比较常用的拟合逼近方法。其中,端点约束条件的选择是非常重要的。本文通过研究三次样条函数插值,把五种不同的端点约束条件应用到实际问题中,针对不同的端点约束,用Matlab计算分析,通过图像及取值比较,从而能得出不同端点约束下插值函数的异同和优缺点。
1 分段三次样条曲线定义与存在性
在实际工程计算中,对数据集进行多项式拟合有许多应用。操作者希望画出经过数据点的无误的光滑曲线。从数学角度分析,在每个区间[xk,xk+1]可构造一个三次函数Sk(x), 使得分段曲线y=S( x)和它的一阶导数和二阶导数在更大的区间[x0, xN]内连续。
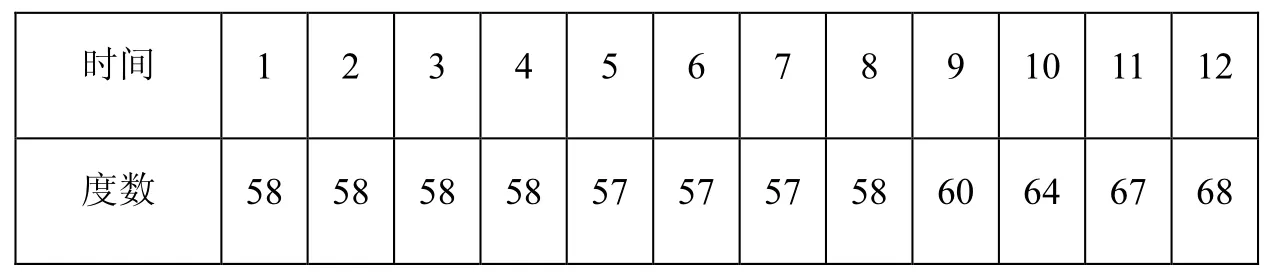
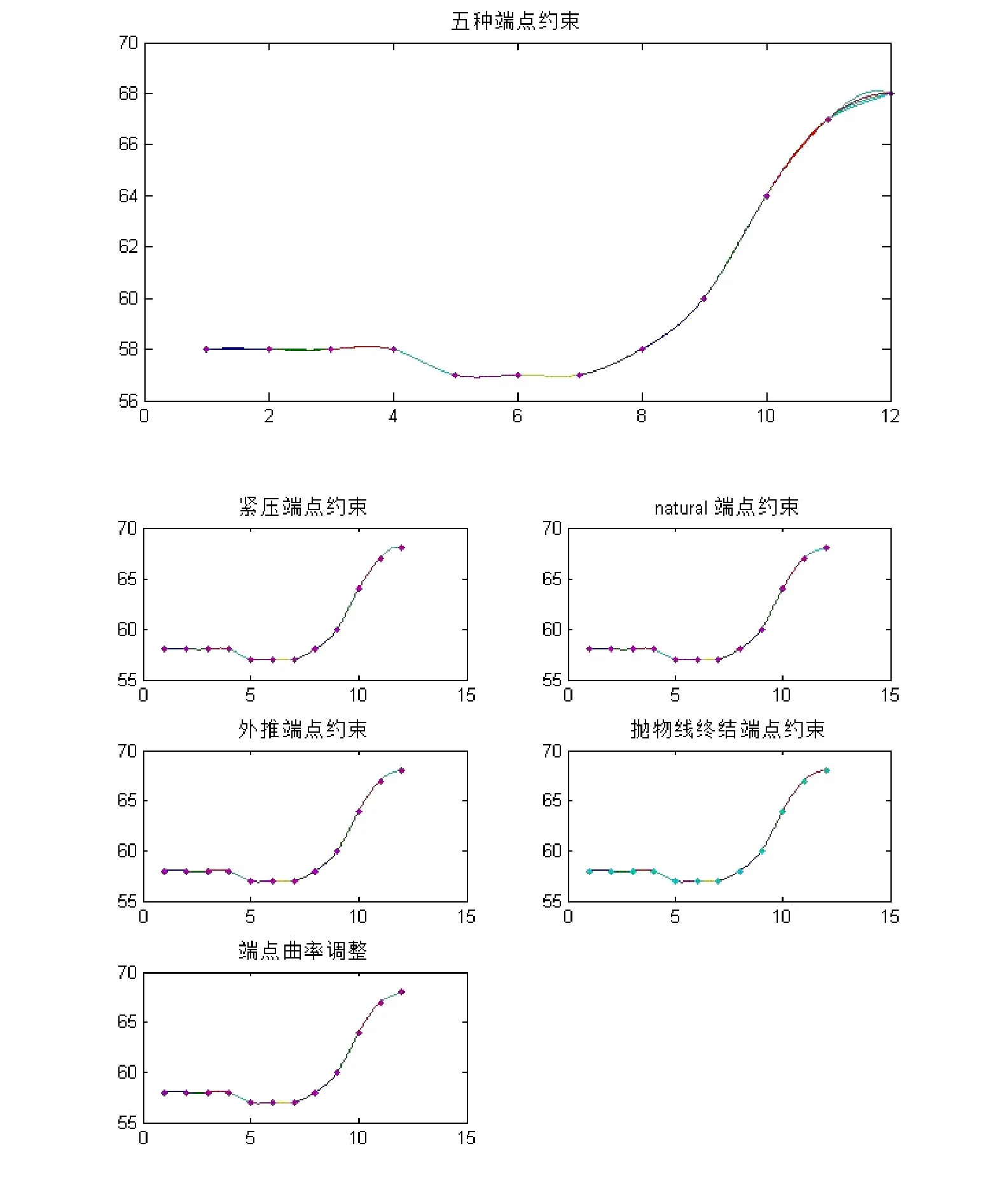
定义[1]设{(xk,yk)有N+1个节点,其中a=x0 (I)S( x)=S(x)=s+s(x−x)+s(x−x)2+s(x−x)3,x∈[x,x],k=0,1,…,N −1 k k,0k,1kk,2kk,3kkk+1 (II)S( xk)=yk,k=0,1,…,N (III)Sk(xk+1)=Sk+1(xk+1),k=0,1,…,N −2 则函数S( x)为三次样条函数。以上性质说明S( x)不仅是由分段三次多项式构成,而且是一个光滑的连续函数。 三次样条的存在性[1]:由于S( x)是分段三次多项式,它的二阶导数S''(x)在区间[x0, xN]内是分段线性的。根据线性拉格朗日插值, S"(x)=(x)可表示为 方程组(1)中的未知数是要求的值{mk}, 其他的项是可以通过数据节点得到的常量。因此,方程组(1)是包含N+1个未知数,具有N−1个方程的不定方程组。需要另外两个方程才能求解,可通过它们消去方程组(1)中的m0和mN。针对端点,采取不同的端点策略[2]。 (IV)S''(x)是靠近端点的常量:m0=m1, mN=mN−1 (V)在每个端点处指定S''(x):m0=S''(x0),mN=S''(xN) 以策略(Ⅴ)为例,如果给定m0,方程组(1)的第一个方程为 如果给定Nm,方程组(1)的最后一个方程为 如果不考虑具体策略,根据(1), (2), (3), 可得到一个包含m1, m2,…mN−1的三角线性方程组 下面讨论针对不同的端点约束,所得到的方程组的形式。 (II)natural样条:S'( a)=0,S'( b)=0,此时方程组(4)的形式为 (III)外推样条:通过对点1x和2x外推得到''()Sa, 对1Nx−和2Nx−外推得到''()S b, 此时,方程组(4)的形式为 (IV)抛物线终结样条:在区间[x0, x1]内,令S'''(x)=0, 在区间[xN−1,xN]内,令S'''(x)=0, 此时,方程组(4)的形式为 (V)端点曲率调整样条:S''(a),S''( b)是确定的值,此时,方程组(4)的形式为 下表给出洛杉矶郊区12小时内每个小时的温度(华氏温度)[1]。对这些数据利用不同的端点约束进行三次样条插值。 表1 温度表Tab. 1 Thermometer 算法与步骤: ①输入N+1个插值节点a=x0 ②计算步长hk=xk+1−xk, k=1,2,…,N −1 ③计算uk=6(dk−dk−1),k=1,2,…,N −1 ④根据不同端点约束条件计算m0, mN ⑤分别用追赶法求三对角方程组(4)得到不同条件下的m1, m2,…,mN ⑥输出各区间Sk(x)的表达式,然后用Matlab画图,分别得到插值曲线如下图。 图1 不同端点约束条件下的插值曲线Fig. 1 The interpolation curves of the different endpoints 从图1中可以看出,对于五种端点约束,左端点高度一致,右端点处差别较大。在一些问题中,可以采取混合端点条件得到更多的样条形式。样条插值是分段三次多项式插值,不存在高次的插值函数,并且三次函数在节点处保持了较好的光滑性、连续性,插值效果在一定程度上优于拉格朗日插值。从应用中也可以看出,对于曲线较平坦的地方,即使节点间距离很大的曲线的逼近效果仍然是很好的[3]。本文通过构造不同的端点约束条件,编制了通用的Matlab程序,直观地了解了三次样条插值的优缺点,在实际问题的计算中起到了一定的作用。 [1] MATHEWS J H, FINK K D. 数值方法[M]. 第四版. 北京: 电子工业出版社, 2005. [2] 金坚明. 论一阶、二阶导数端点存在误差对三次样条插值函数的影响[J]. 数学的实践与认识, 1987(2): 96-98. [3] 曹德欣, 王海军. 三次样条插值函数的数值稳定性[J]. 中国矿业大学学报: 自然科学版, 2001(2): 213-216. Structure and Matlab Implementation of Cubic Spline Interpolation Endpoint Constraints XING Li Spline interpolation techniques are increasingly important in engineering calculations. The boundary conditions of the cubic spline interpolation are given according to the actual problem in the state of the endpoint. Through researching cubic spline function interpolation constraints for different endpoints, using Matlab computational analysis, each interval segment cubic spline function body expression is showed. The point of interpolation is calculated and each interval segment graph is displayed which is applied to practical problems. Endpoint constraints as well as mixed boundary conditions is focused on. computational mathematics; cubic spline interpolation; endpoint constraints; Matlab P315.31 A 1001-4543(2012)04-0319-05 2012-09-24; 2012-11-20 邢丽(1978-),女,山东人,讲师,硕士,主要研究方向为偏微分方程数值解,电子邮箱xingli@sf.sspu.cn。
2 端点约束




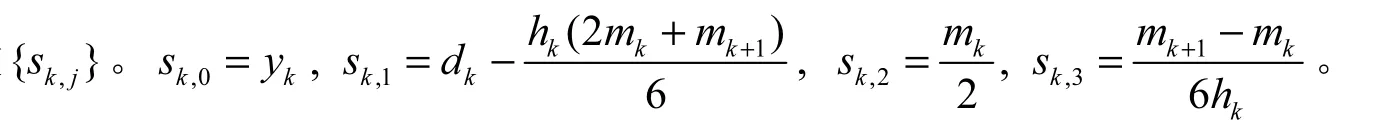

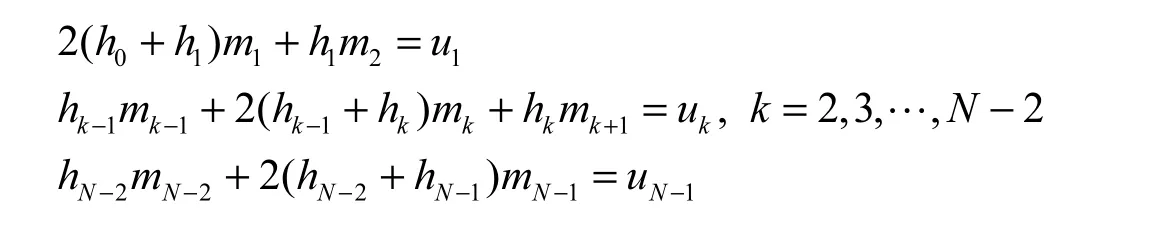

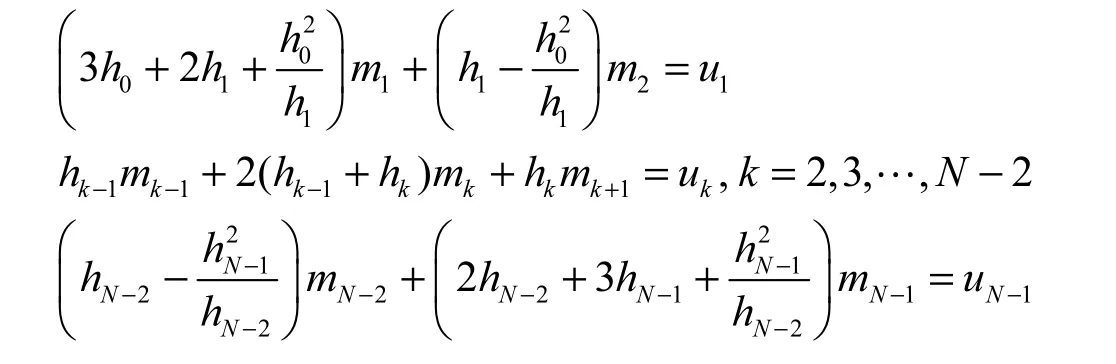
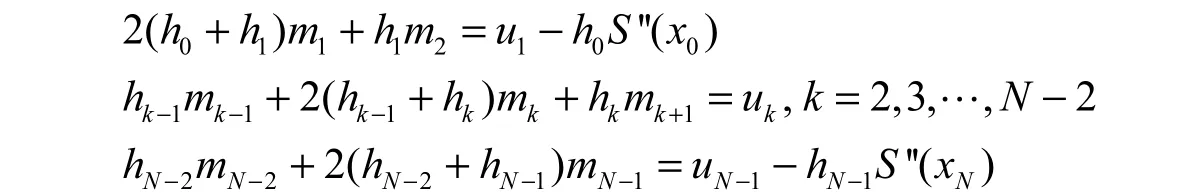
3 数值例子
4 结论
( Department of Applied Mathematics, Shanghai Second Polytechnic University, Shanghai 201209, P. R. China )
