一类Lotka-Volterra系统的平均持续生存性
2012-08-16韩欣利潘丽君
韩欣利,潘丽君
(1. 南京邮电大学理学院,南京210046;2. 南京航空航天大学数学系,南京211106)
一类Lotka-Volterra系统的平均持续生存性
韩欣利1,潘丽君2
(1. 南京邮电大学理学院,南京210046;2. 南京航空航天大学数学系,南京211106)
研究了非自治捕食被捕食Lotka-Volterra系统的平均持续生存性。通过引入新的研究方法,建立了一系列关于Lotka-Volterra系统正解的平均持续生存性的积分形式的新准则,并研究了一致弱平均持续生存性和弱平均持续生存性的等价性。
非自治;捕食被捕食;Lotka-Volterra系统;平均持续生存性
0 引言
两种群Lotka-Volterra系统是Guass和Witt在1935年建立的,两种群非自治捕食被捕食系统形如(详见文献[1~6]及其中所引用的文献)
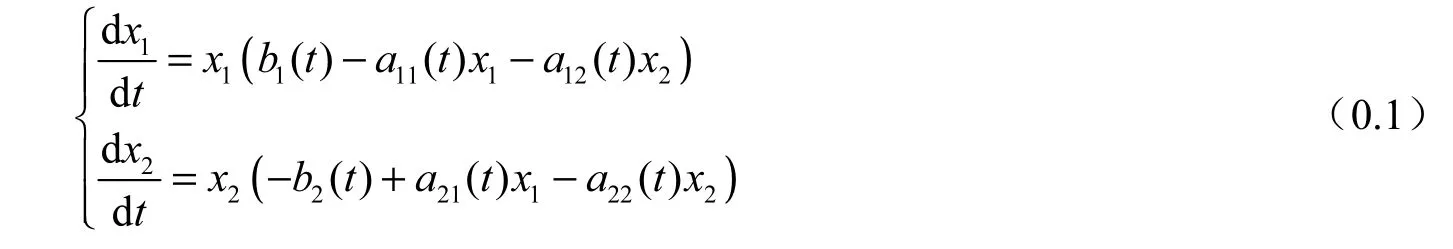
从生物学的角度看,平均持续生存性是指从平均的角度看某一种群在未来时间里数量大于零,即该种群不会灭绝。而在数学上,种群的平均持续生存性具有严格而规范的定义。
设x( t)=(x1( t),x2( t ))是系统(0.1)的任意一个正解,则
(1)种群xi( i=1,2) 称为弱平均持续生存的(WAP),若
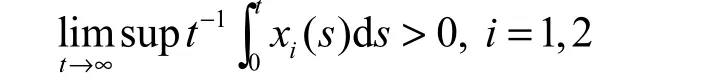
(2)种群xi( i=1,2) 称为强平均持续生存的(SAP),若

(3)种群xi( i=1,2) 称为一致弱平均持续生存的(UWAP),若存在一个不依赖于系统(0.1)的正常数m>0, 使得
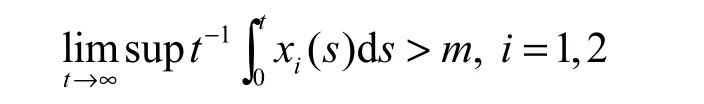
(4)种群xi( i=1,2) 称为一致强平均持续生存的(USAP),若存在一个不依赖于系统(0.1)的正常数m>0,使得
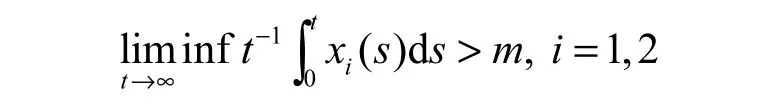
研究种群的平均持续生存性对于研究动物种群的增长规律,特别是在动物保护和生态环境的治理和开发等领域都有着重要的作用。本文主要研究非自治捕食被捕食Lotka-Volterra系统(0.1)的平均持续生存性。通过引入新的研究方法,建立一系列关于Lotka-Volterra系统(0.1)的正解平均持续生存性的积分形式的新准则,并研究一致弱平均持续生存性和弱平均持续生存性的等价性。本文的安排如下:在第1节中,我们将给出预备知识与基本假设;在第2节中,我们将陈述并证明关于平均持续生存的主要结论。
1 预备知识
1.1 基本假设

1.2 重要引理
在本节的最后我们将给出本文需要用到的两个引理。
首先,我们考虑如下单种群非自治的Logistic系统:

我们有如下的结论。
引理1.1 如果系统(1.1)满足下列假设:

(i)存在常数01M>, 使得对系统(1.1)的一切正解1()x t都有
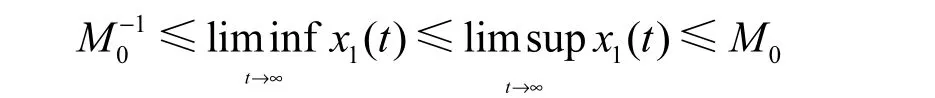
引理1.1的证明详见文献[5]中的引理1。

引理1.2的证明详见文献[3]中的引理4。
2 平均持续生存性
设10()xt是系统(1.1)的一个固定的正解。关于系统(0.1)的平均持续生存性,我们有如下的结论。
定理2.1 假设(LV1),(LV2),(LV4)和(LV5)成立,则对于系统(0.1),有
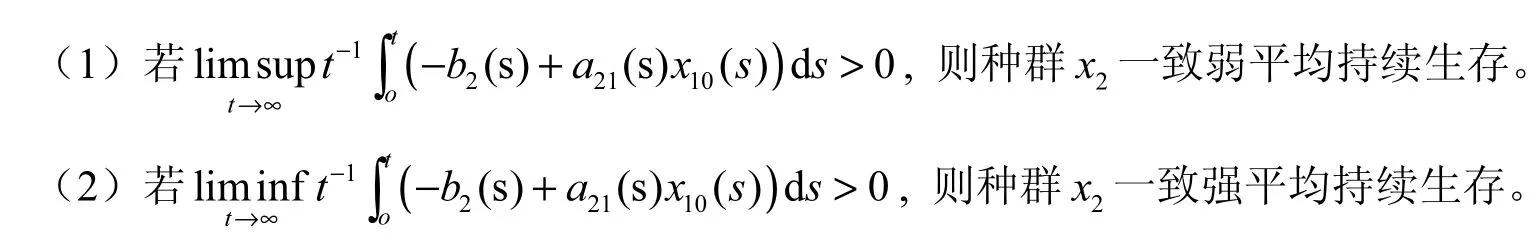
其中x10为系统(1.1)的正解。
证明 首先考虑单种群非自治的Lotka-Volterra系统(1.1)。由(LV1)和(LV4),系统(1.1)满足引理1.1的所有条件,因此,若( t)和(t)是系统(1.1)的任意两个正解,则(t ))=0, 并且存在与任意正解t)无关的常数M0>1, 使得

由(2.2)和系统(1.1)的全局渐近稳定性,并根据比较定理可以得到:对任意的ε>0, 存在常数T=T(ε)>0,使得对一切t≥T都有

由(2.1), (2.3)以及(LV5)知,系统(2.1)的所有正解均在R+0上有定义且最终有界,设其界为M=max{L1, K}。
下面我们将分两部分给出定理2.1的证明:
(I)对一切t≥0, 有x1( t)≥x10(t)。
结合(2.3)可知, 对任意的ε>0, 都存在常数T=T(ε)>0,使得对一切t≥T都有x10(t)≤x1( t)≤x10(t)+ε,这表明lti
→m∞(x1( t)−x10(t ))=0, 由此可得

由系统(0.1)的第2个方程,并根据微分中值定理可得

因此,由(2.5)~(2.7)以及定理2.1的条件(1),有

由(2.5)~(2.7)以及定理2.1的条件(2),有

(II)存在常数T>0,使得x1( T) 由(3.2)及比较定理可得,对一切t≥T,有x( t) 并且根据微分中值定理可得 因此,根据(2.8)知,当tT≥时, 现在考虑系统(0.1)的第2个方程,由(2.9)并根据微分中值定理可得,对一切tT≥, 进而由(LV2)和(2.9),还可以得到,对一切tT≥, 因此,对一切tT≥, 有 显然,存在常数1M,使得 由(2.1),(2.10),(2.11)以及1()x t和2()x t在0R+上的有界性,有 由不等式(2.10)可得 于是,由(2.12),(2.13)以及定理3.1的条件(1)可得: 这表明种群x2是一致弱平均持续生存的。 由不等式(2.10),我们还可以得到 于是,由(2.12),(2.13)以及定理2.1的条件(2)可得 这表明种群x2是一致强平均持续生存的。 因此,由(I)和(II)两部分可知,定理2.1的结论成立。 定理3.2 假设(LV1)和(LV3)∼(LV5)成立。若对于系统(0.1),种群x2是弱平均持续生存的,则(−b( s)+a(s) x(s))ds >0, x(t)是系统(1.1)一个固定的正解。2211010 2 由(2.14)以及种群2x的有界性我们还能得到 由微分中值定理有 类似于定理2.1的证明,接下来我们将分两部分来给出定理2.2的证明。 (I)对一切t≥0都有x1( t)≥x10(t)。 从而,由(2.14)~(2.16)和(LV3)知,对上述的时间序列, 有 (II) 存在常数T≥0, 使得x1( T) 由(2.2)并根据比较定理可得,对一切t≥T, 都有x1( t) 因此,由(2.14)和(2.15)知:对上述的时间序列{tn},有 从而,由(I)和(II)两部分可知,定理2.2的结论成立。 结合定理2.1与2.2,我们有下面的结论: 定理2.3 假设(LV1)(LV5)∼成立。对于系统(0.1),下面的陈述式等价的: (1)种群2x是弱平均持续生存的。 (2)种群2x是一致弱平均持续生存的。 [1] TENG Z D. Uniform persistence of the periodic predator-prey Lotka-Volterra systems[J]. Appl. Anal., 1999,72(3-4): 339-352. [2] 韩欣利. 一般非自治捕食被捕食Kolmogorov型系统研究[D]. 乌鲁木齐: 新疆大学理学院, 2004. [3] ELLERMEYER S F, PILYUGIN S S, REDHEFFER R. Persistence criteria for a chemostat with variable nutrient input[J]. J. Diff. Equations, 2001, 171(1): 132-147. [4] 滕志东, 陈兰荪. 非自治竞争Lotka-Volterra系统的持续生存和全局稳定[J]. 高校应用数学学报A辑(中文版), 1999, 14(2): 141-146. [5] TENG Z D, LI Z M, JIANG H J. Permanence criteria in nonautonomous predator-prey Kolmogorov systems and its applications[J]. Dynamical System, 2004, 19(2): 171-194. [6] XIAO D M, RUAN S G. Global analysis in a predator-prey system with nonmonotonic functional response[J]. SIAM J. Appl. Math., 2001, 61(4): 1445-1472. On the Average Persistence of A Lotka-Volterra System HAN Xin-li, PAN Li-jun The average persistence of a nonautonomous predator-prey Lotka-Volterra system is investigated. By introducing a new method, a series of new criteria on the average persistence of the Lotka-Volterra system is constructed. Also, the equivalence of the uniformly weak average persistence and weak average persistence are studied. nonautonomous; predator-prey; Lotka-Volterra system; average persistence O175.13 A 1001-4543(2012)04-0307-08 2012-10-31; 2012-12-07 韩欣利(1978-),男,山东烟台人,讲师,博士,主要研究方向为常微分方程研究,电子邮箱xinlihan@126.com。 江苏省高校自然科学研究项目(No. 12KJB110017);南京邮电大学引进人才基金(No. NY208028和No. NY211140)南京航空航天大学科研基金(No. NN2012048)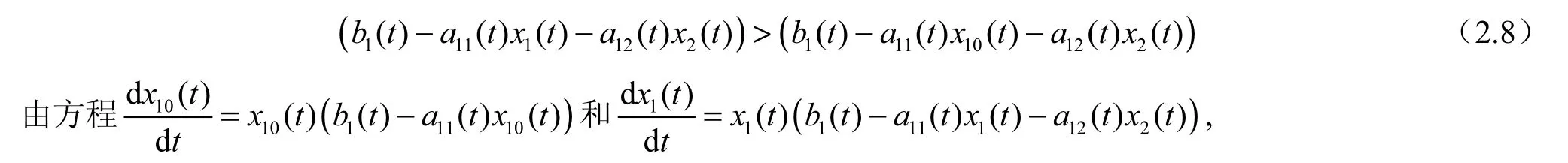
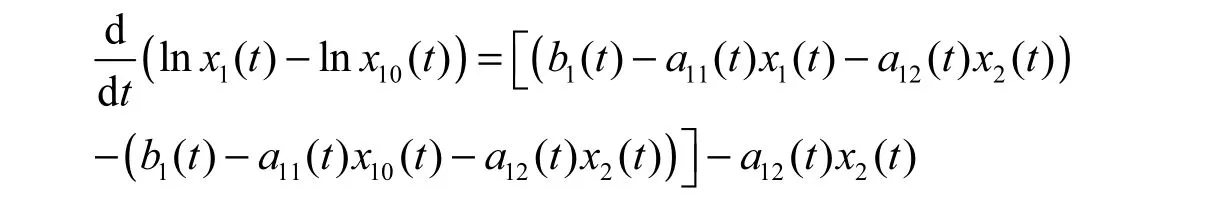

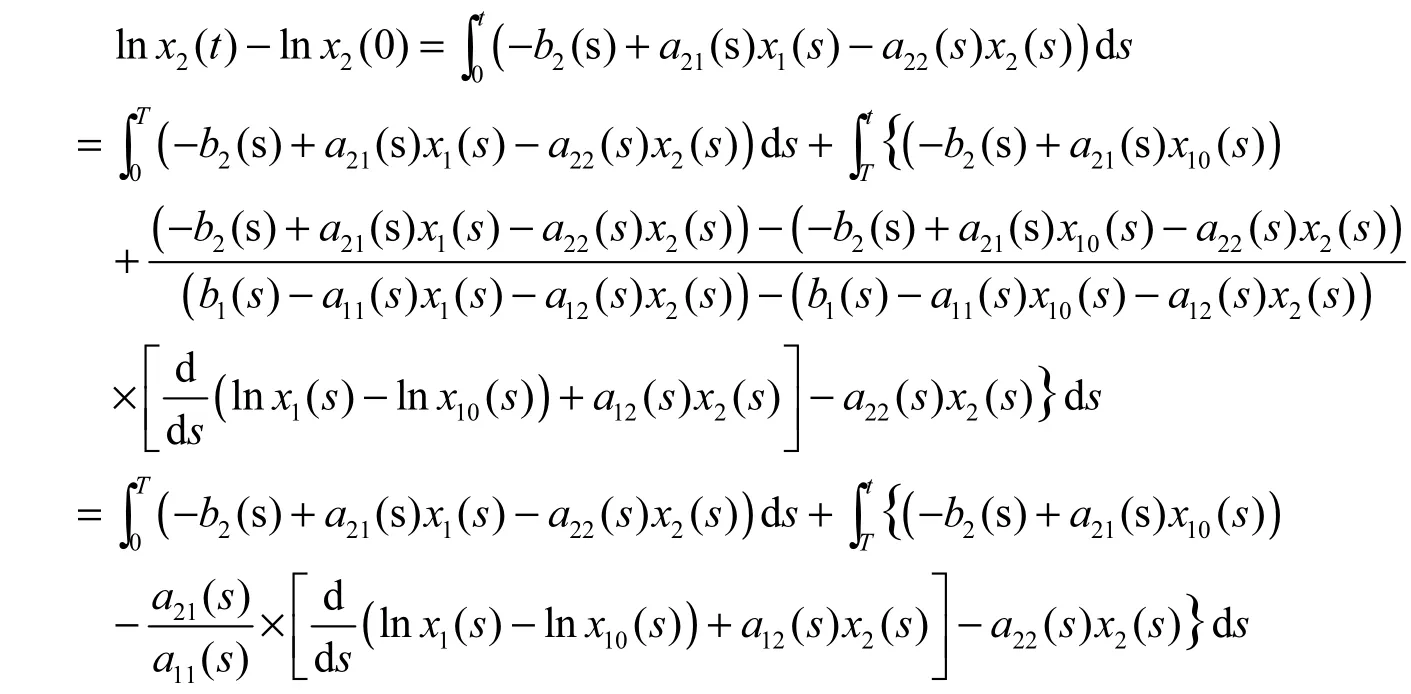
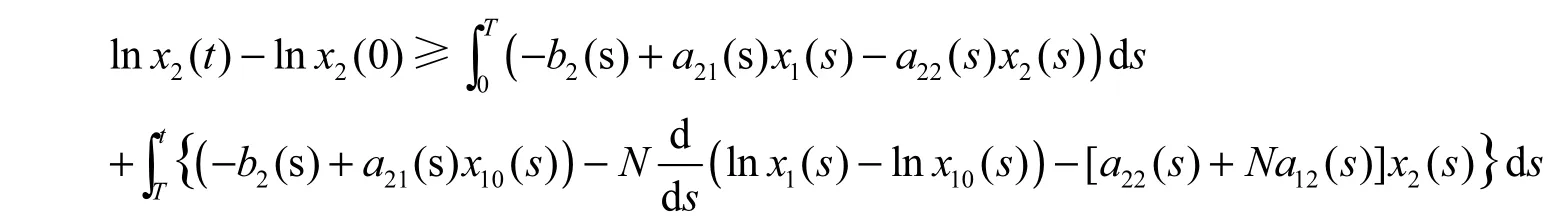
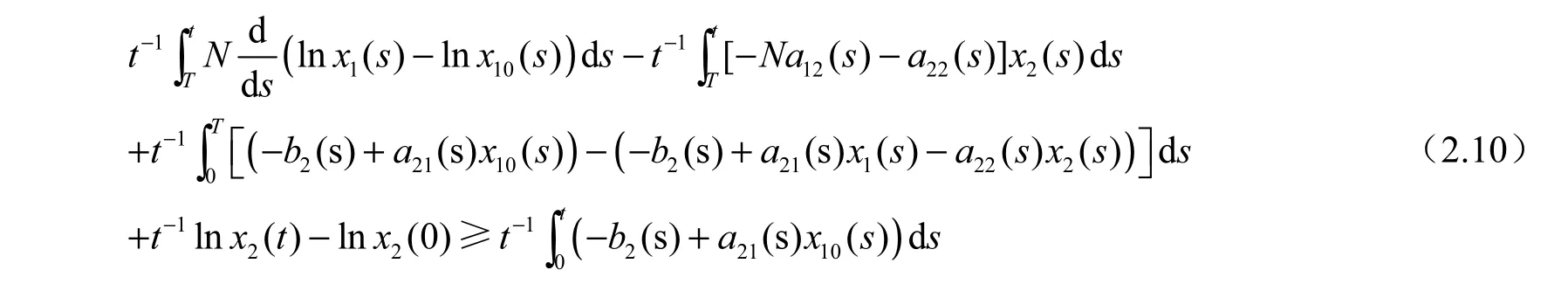



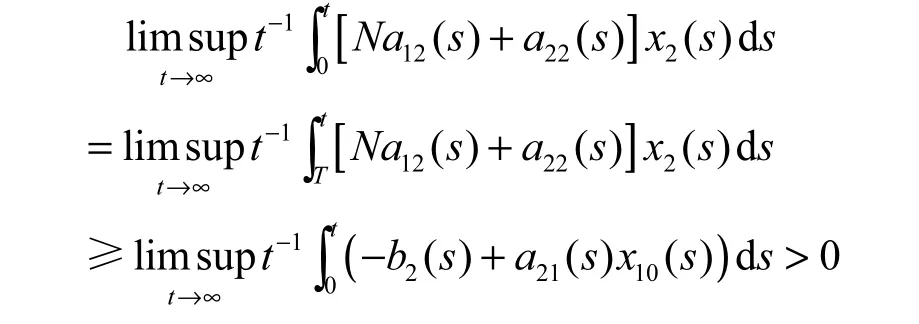
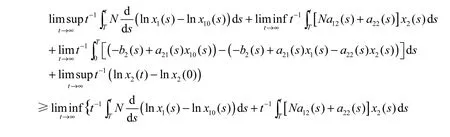
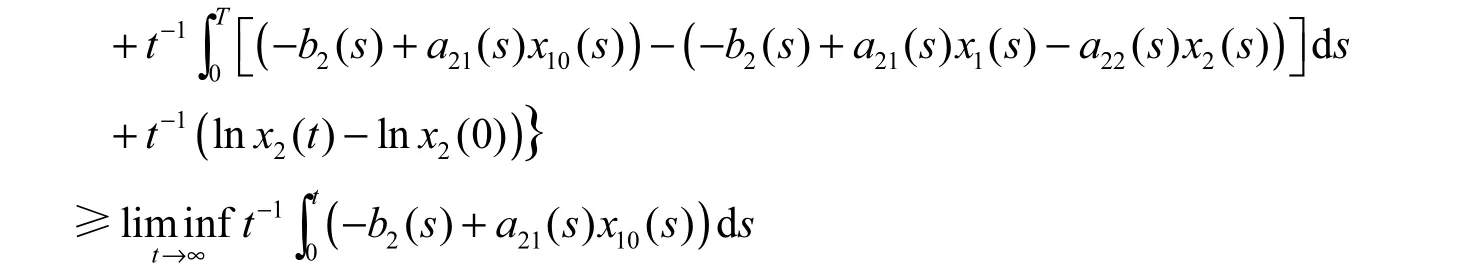
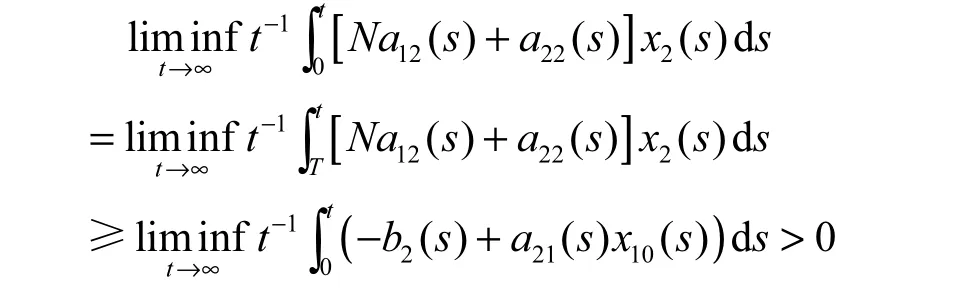



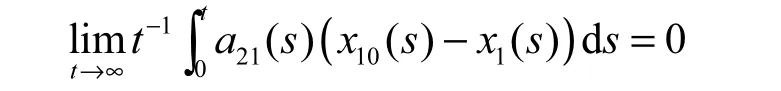
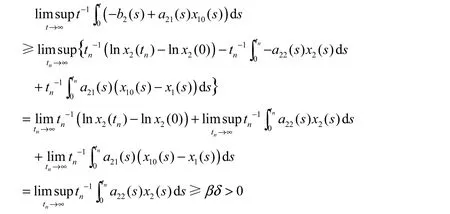
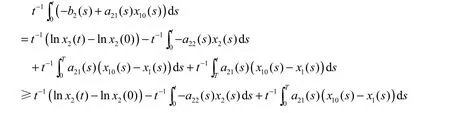
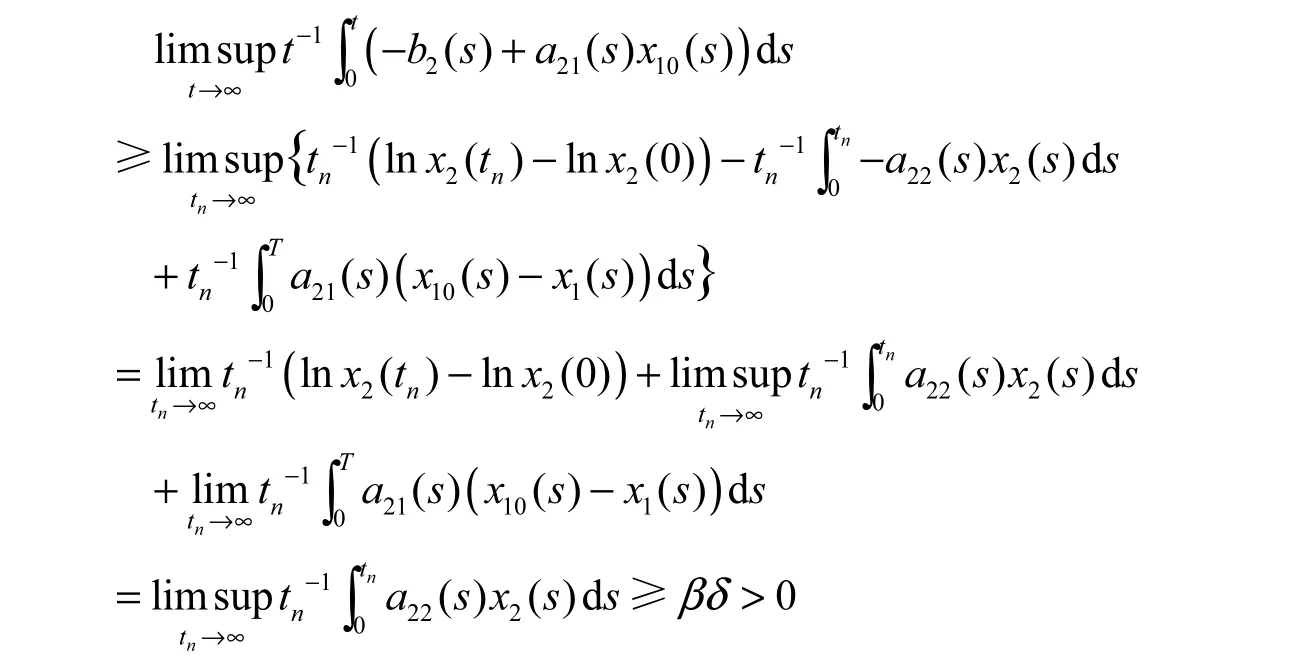

( 1. School of Science, Nanjing University of Posts & Telecommunications, Nanjing 210046, P. R. China; 2. Department of Mathematics, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, P. R. China )
