连接体模型的变式迁移——谈2011年高考江苏卷物理

邱勤薇

（苏州大学 江苏 苏州 215006；苏州第十中学 江苏 苏州 215006）

1 引言

为了达到选拔的目的，每年的高考题都会出现一些“新面孔”，而所谓的新题更多的还是“新瓶装旧酒”，即在原有模型基础上的变式而已.解题的关键是要能抓住其内在的联系，把握知识迁移的规律.

纵观2011年高考江苏卷，有两道涉及连接体模型的题目就很好地体现了变式迁移的思想.计算第14题是传统的轻绳模型；而多项选择第9题则是新颖的轻绸模型，学生往往被其陌生的情境所迷惑.若能与第14题相结合找到相似点切入，问题定能迎刃而解.

现对这两道题目进行分析与讨论，以期挖掘其中“变异”的精髓，为物理教学提供借鉴.

2 两种轻质模型的类比迁移

2.1 轻绳模型

【例1】（2011年高考江苏卷第14题）如图1所示，长为L，内壁光滑的直管与水平地面成30°角固定放置.将一质量为m的小球固定在管底，用一轻质光滑细线将小球与质量为M＝km的小物块相连，小物块悬挂于管口.现将小球释放，一段时间后，小物块落地静止不动，小球继续向上运动，通过管口的转向装置后做平抛运动，小球在转向过程中速率不变.（重力加速度为g）

（1）求小物块下落过程中的加速度大小；

（2）求小球从管口抛出时的速度大小；

图1

解析：轻绳质量为零，由牛顿第二定律，F合＝ma＝0，可得绳中拉力处处相等.

（1）当M未落地时，两物体构成连接体，加速度的方向虽不同，但大小相同，可用整体法求加速度

（2）小物块M落地后，绳子松弛，可将连接体变为单个物体m匀变速直线运动处理.以下求解过程就不再赘述.

小结：此类连接体模型是通过轻绳连接两个物体，由绳中拉力处处相等，故得物体所受拉力相等，只要绳不松、不断，两物体便以大小相等的加速度运动.一旦两者出现相对运动，连接体系统即被破坏.可以说轻绳模型是相对容易辨识的“显性连接”.

2.2 轻绸模型

【例2】（2011年高考江苏卷第9题）如图2所示，倾角为α的等腰三角形底面固定在水平面上，一足够长的轻质绸带跨过斜面的顶端铺放在斜面的两侧，绸带与斜面间无摩擦.将质量分别为M和m（M＞m）的小物块同时轻放在斜面两侧的绸带上.两物块与绸带间的动摩擦因数相等，且最大静摩擦力与滑动摩擦力大小相等.在α角取不同值的情况下，下列说法正确的有

A.两物块所受摩擦力的大小总是相等

B.两物块不可能同时相对绸带静止

C.M不可能相对绸带发生滑动

D.m不可能相对斜面向上滑动

图2

解析：此题是涉及绸带、质量为M和m的物块三个物体的连接体问题.由于轻质绸带的引入，学生对此情境感到陌生，很难把握解题的突破点，要解此题，必须要有很好的物理素养及透过现象看本质的“火眼金睛”.现分析如下.

（1）初始条件：α角很小时，即μ＞tanα，分别以物块M，m为研究对象，受力分析如图3所示，所以

故初始状态物块M和m及绸带相对静止，又因为绸带与斜面间无摩擦，所以三者以相同大小的加速度运动，方向如图3所示.

图3

整体法：以物块M，m和绸带为研究对象，应用牛顿第二定律，得

隔离法：分别对绸带、物块M和m应用牛顿第二定律.

对绸带受力分析如图4所示，（平衡的支持力和压力未标出）

图4

因绸带轻质，m＝0，则

上式为本题的关键突破点.

对物块M有

对物块m有

（2）动态分析：当α角增大时，由上式可知f1，f2均增大.

（3）临界条件：当f2＝μmgcosα＝f2max时，有

故物块m将先相对绸带向下滑动，而此时物块M仍与绸带保持相对静止.

（4）最终趋势：此后，物块M与物块m的加速度大小将不再相等，但连接体系统并未破坏，物块与绸带间摩擦力大小仍相等，只是物块M受的是静摩擦，而物块m受的是滑动摩擦.因为

故物块M所受的静摩擦力永远小于其最大静摩擦力，不可能相对绸带滑动.

（5）分析至此，此题的答案为选项A，C便一目了然了.

小结：此类连接体模型是轻绸通过摩擦力连接两个物体，因轻绸两端受力平衡，故两物体受到的摩擦力大小相等，可将此题情境用轻绳模型来等效处理，如图5所示.而图5与例1是异曲同工的，如果能将轻绳变化为轻绸，将拉力变化为摩擦力，不就类似例2了吗？当然也要看到轻绸的特别之处，即两物体可以相对滑动.由于两者所受摩擦力依然相等，仅性质发生变化，故连接体系统依然存在.即轻绸模型是“隐性相连”，谓之“牵而不连”.

图5

此外，例2除了轻绸模型外，还蕴含了多个处理物理问题的典型方法，如整体法、隔离法、动态分析法、临界分析法、理想模型法，不失为难得一见的好题.

3 非理想模型的讨论

前面一直在讨论轻质的理想模型，若进一步迁移变化，令上述例2要考虑绸带的质量，那么会得到怎样的结果呢？（就实际的问题而言，是不存在质量为零的物体的）

研究的前提是足够长的绸带，即铺满整个斜面，这样就可以不用考虑绸带的重力产生的效果，因为两侧可以相互抵消.然后的分析就和上面一样，只要加入绸带的质量m0就可以了.

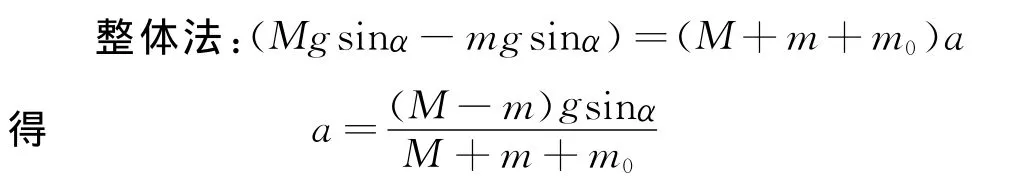
隔离法：对绸带

对物块M

对物块m

所以

当f2＝f2max＝μmgcosα时，有

所以f1＜f1max

故结论与轻质绸带的相同.通过定量计算，透过现象看本质，即使是非理想情况，亦可分析到位.

4 结束语

笔者认为在一张高考卷中出现两道同一模型的连接体问题，应该不是简单的巧合，而是命题者的精心设计，在变式中体现创新，在创新中提升能力.考生要能顺利完成这类问题，除了要有扎实的基本功，还要有灵活的思维，敏锐的洞察力.这当然与考生的能力分不开，但也启示教师要在平时的教学尤其是复习课中，注重一题多变，情境迁移的训练，以拓宽学生的思路，培养灵动且有创造力的人才.