基于极限平衡法的边坡稳定性分析

邱 阜 彭振斌

（1.中南大学地球科学与信息物理学院 湖南 长沙 410012；2.长沙市天心区建设局 湖南 长沙 410000）

0 引言

边坡稳定性分析方法主要分为极限平衡法与数值分析方法，极限平衡方法分析边坡稳定性具有简单、快捷的特点。而数值分析方法主要利用数值计算软件对边坡开挖、支护过程进行模拟，计算精度较高，但由于建模分析相对繁琐，在工程中并未得到广泛的推广应用。 随着计算机水平的发展，极限平衡方法逐渐被软件化，出现了以geo-studio、slide 等为代表的一批基于极限平衡方法的边坡计算软件，为相关工程的设计计算提供了方便，并得到了广泛的应用。 如万文[1]运用极限平衡法对某高速公路边坡稳定性及支护措施进行了模拟，探讨了Janbu 法、Bishop 法、Morgenstren-Price 计算方法在边坡稳定性计算中的不同点。 得到了一些有益的结论。 而曾铃[2]运用极限平衡方法对某边坡滑移面的抗剪强度参数进行了反演分析，得到了与实际相符的计算参数。 由此可见，利用极限平衡方法分析边坡稳定性已经得到了广泛应用。 因此，本文在总结前人研究成果的基础上， 基于极限平衡计算软件，对某边坡初始稳定性及处治措施进行了研究，为设计与施工提供了参考依据，具有一定的现实意义。

1 极限平衡计算原理及方法

1.1 极限平衡计算原理

分析岩体和土体稳定性时假定一破坏面, 取破坏面内土体, 为脱离体计算出作用于脱离体上的力系达到静力平衡时所需的岩土的抗力或抗剪强度, 与破坏面实际所能提供的岩土的抗力或抗剪强度相比较,以求得稳定性安全系数。安全系数根据定义可表示为[3]：

式中：Fs为安全系数，τf为滑动面上的抗滑力，τ 为滑动面上的实际滑力。

极限平衡分析方法最早是1961 年由瑞典人彼得森提出来的，他将边坡潜在滑移面以上的土体划分成若干个垂直条块，在计算过程中进行了一定的假设，假设条块间没有相互作用力的存在，定义安全系数为潜在滑移面上的抗滑力矩与滑动力矩之比为边坡安全系数。 随着科学技术的研究的不断深入，广大学者在此基础上对其进行了优化[4-5]，出现了以Bishop 法、Janbu 法、Morgenstren-Price 等一系列简化方法。 限于篇幅本文只对Bishop 法进行详细介绍。

1.2 Bishop 简化计算方法

简化的Bishop 法假设滑移面的形状为圆弧形[6-7]，土条之间只有水平推力，条间剪力为零，计算见图如图2 所示。

图1 BISHOP 计算简图

作用在第i 条块上的力有重力（W）、开挖面的法向力（Nci）和切向力（Tci）、条块分界面上的法向力（Ei，Ei-1）和切向力（Xi，Xi-1）以及潜在滑动面上法向力（Ni）和切向力（Ti）。 li为第i 条块底边长度，αi为第i 条块底边与水平面的夹角，ci为第i 条块的岩土体内聚力，φi为第i 条块岩土体的内摩擦角。

土条间满足:

假定土坡安全系数为K， 则土条i 滑动面上的切向力满足以下关系：

联立式（2）和式（3）得

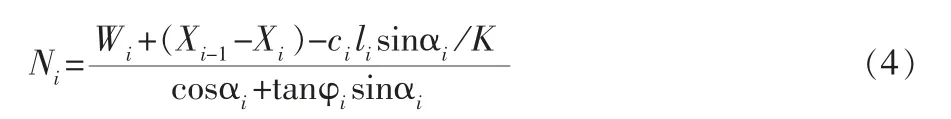
根据边坡安全系数定义

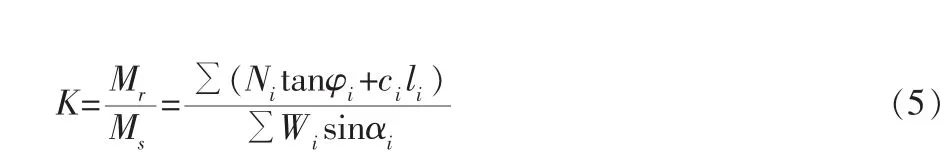
整理得:

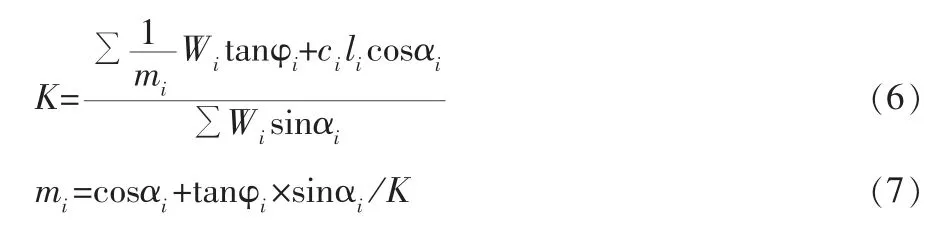
2 工程概况

长沙市天心区新天村安置小区南侧边坡位于长沙市天心区新开铺街道办事处新天村内。 该边坡高约7-14m 边坡，边坡分为三级，从上往下分别高4 米、7 米、3 米，坡顶有一平房。边坡做了简易挂网喷浆处理，2011 年1 月8 日，边坡体由于降雨发生了潜在的滑坡， 在其牵引力作用下产生了张裂缝，其稳定性受到了破坏，在有关专家指导下进行了坡脚反压与坡顶卸载相结合的抢险处理， 坡体基本处于稳定状态。因此需对其进行支护处理， 以保证其边坡的长期稳定性，边坡典型剖面见图2 所示。

根据钻孔柱状图可知，各岩土层成层条件为：

（1）粉质粘土：灰白、褐黄色，沉积层理清晰可辨，含薄层粘土，稍湿，硬塑～坚硬状态。

（2）中砂：褐黄色，石英质成分，不均匀含圆砾5-10%，混5-10%粘性土，稍湿，中密状态。

（3）粗砂：褐红色，石英质成分，不均匀含圆砾5-15%，混7-15%粘性土，中湿，中密状态。

根据勘察报告，地下水类型为上层滞水及潜水，上层滞水水量有限，潜水水量较大。 水质分析表明，场地地下水对混凝土结构、混凝土中的钢筋无腐蚀性，对钢结构具弱腐蚀性。

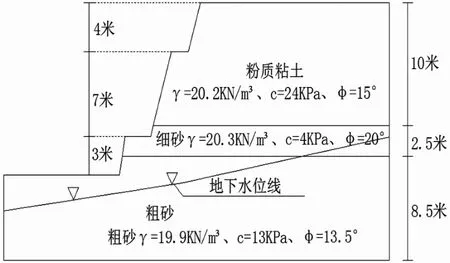
图2 边坡典型剖面

3 边坡稳定性分析

图3 边坡典型剖面数值计算模型

3.1 边坡计算模型的建立与计算参数

为了分析该边坡的稳定性， 并提出合理的治理方案，本文选取边坡最危险剖面作为稳定性分析的对象，以保证其边坡稳定性能够得到最大的保障，与图2 想对应的边坡典型剖面数值分析模型如图3 所示。

为了准确、可靠地对边坡稳定性进行分析，以起到为边坡的治理提供科学的的依据的目的，本文选用勘察资料所述各钻孔土样抗剪强度平均值为最终计算值，各层岩土体物理力学参数见表1。

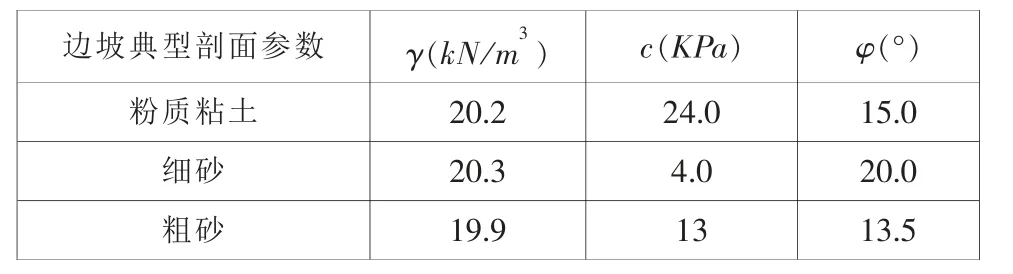
表1 边坡物理力学参数

3.2 无支护条件下边坡稳定性分析

图4 为边坡在自然无支护条件下的潜在滑移面相对位置图，有图可知，边坡安全系数为0.998，其安全系数的大小不能满足规范所要求的最小值。 由此可见：边坡在无支护条件下的稳定状态与实际观测所得到了稳定性结论一致。 在无支护条件下能够基本稳定， 但不能满足规范所规定的最小值。 因此，需对边坡进行治理，以保证其长期稳定性。

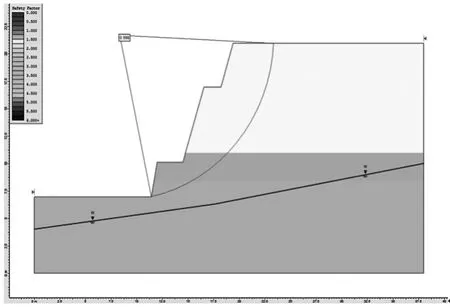
图4 无支护条件下边坡滑移面位置（Fs=0.988）

3.3 有支护条件下边坡稳定性分析

鉴于边坡在自然无支护条件下不能满足其稳定性的现状，笔者拟采用设计资料所推荐的边坡治理方式对边坡进行处治。 根据设计院推荐支护方式，采用如图5 所示支护形式对边坡进行支护。 其中，锚索抗拉强度为150kN，锚定板强度为150kN，粘结强度为2000kN/m，剪切强度为80kN。

利用极限平衡方法，对边坡在图5 所示支护措施条件下的稳定性进行计算，计算结果如图6 所示，有图可知，边坡在锚索支护后安全系数为3.014， 大于规范所要求的最低安全系数标准，表明边坡处于安全状态。 由潜在滑移面的相对位置可知， 边坡在该支护措施下发生浅层滑移的可能性较低，具有较高的安全保障。 由此可见，设计院所推荐的支护措施是行之有效的，能保证边坡的长期稳定性。

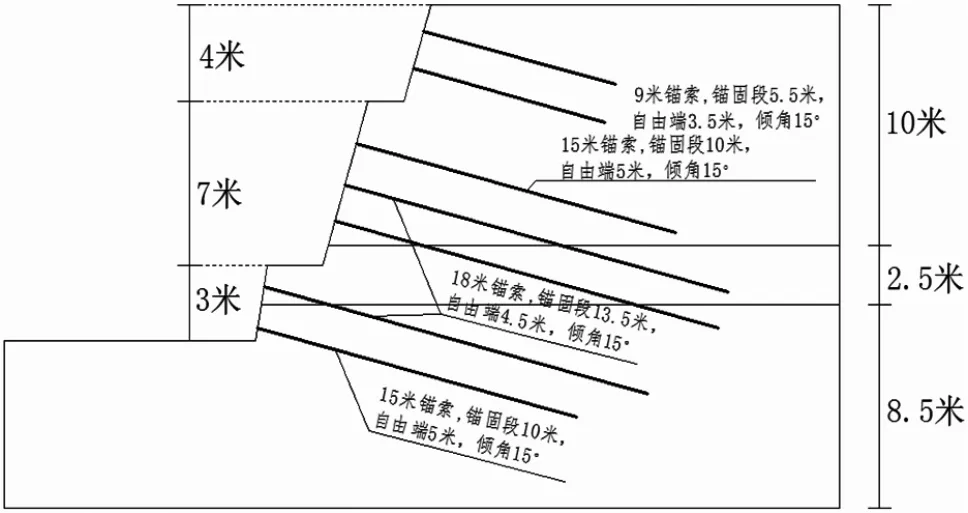
图5 边坡支护措施设计图

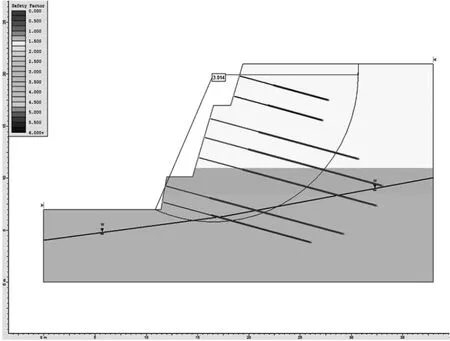
图6 有支护措施条件下边坡稳定性计算结果（Fs=3.014）

4 结论

本文基于实际岩土体物理力学参数， 利用极限平衡方法，对边坡支护前后的稳定性进行计算分析，分析表明：

4.1 该边坡在无支护条件下，安全系数为0.998，边坡处于极限稳定状态，与实际监测数据所呈现状态想吻合，边坡需进行及时治理。

4.2 依据设计院所推荐支护措施，对边坡进行治理。经计算，边坡在系统锚索支护作用下安全系数显著提高，达到3.014。满足规范岁要求的最低标准。 表明该支护措施对约束文中所述边坡稳定性是行之有效的。

4.3 由计算结果可知， 利用极限平衡方法分析边坡的稳定性具有计算准确、操作简便等特点，具有广泛推广的现实意义。

［1］万文，曹平，吴永恒.弹塑性极限平衡法分析复杂岩质边坡的稳定性[J].中国安全科学学报，2004,14（6）:100-108.

［2］曾铃，蒋中明，付宏渊.边坡潜在滑移面抗剪强度参数反演研究[J].中外公路，2011,31（1）:23-25.

［3］李广信.高等土力学[M].北京：清华大学出版社，2004.

［4］黄梦宏，丁桦.边坡稳定性分析极限平衡法的简化条件[J].岩石力学与工程学报，2006，25（12）:2529-2536.

［5］钱家欢，殷宗泽.土工原理与计算[M].2 版.北京：中国水利电力出版社，1996.

［6］Bishop A W，Alpan I,Bight G E，et a1.Factor controlling the shear，tren -gth of partly saturated cohesive soil [S].In ASCE Research Camferen on the Shear Strength of Cohesive Soils.Univ.of Colorado，1960，503-532.

［7］Bishop A W.Blight GE.Some aspects of effective stress in saturated and party satu-rated soil[J]. Geotechnique，1963,13（3）：177-197.