浅析苏科版七年级几何教学推理能力的培养

2012-08-16张菊弟

科技视界 2012年18期

张菊弟

（苏州市吴中区东山莫厘中学江苏苏州 215107）

平面几何是运用逻辑推理的方法来研究平面图形性质的一门学科。因此，培养学生逻辑推理的能力是平面几何教学的主要目标之一。是学生学几何的关键，也是学生学几何的难点。虽然学生在小学里接触过一些几何图形，但是现在他们对于逻辑推理的思维方法和过程还是完全陌生的。尽管初中七年级上册还没有要求进行逻辑推理形式的书写，可是到了八年级下册就要求用逻辑推理的形式来解决有关的“证明”了，如果现在不打好基础，那么以后做几何证明题时可能就会感到困难重重！因此，必须要在七年级做好几何教学的推理论证工作，为今后的几何学习打好扎实的基础。下面谈谈本人的一些实践与体会。

1 不该忽视的一类证明，初步感受几何推理论证

图1

图2

平面几何入门学习中，我感觉大多数教师在这一阶段教学中对于利用“等式性质”推导线段和角相等的证明不够重视，而事实上，课本上更有相关的习题要求学生掌握证明，苏科版七年级（上）课本第115 页习题6.13 如图1 如果AC=BD，那么线段AD 与线段BC 之间有怎样的数量关系？说说你的理由。另一个方面是，在教学中我作为一个典型例题重点讲解，而且在黑板上写出严格的推理过程和填上每一步的理由依据，证明：∵AC=BD（已知）

∴AC+CD=BD+CD（等式性质）

即AD=BC

证完结束后，我小结如下：实际上，这道题目是方程中等式性质在几何方面的运用，接着就做一个变式练习：如上图如果AD=BC，那么线段AC 与线段BD 之间有怎样的数量关系？说说你的理由。让学生模仿黑板上的证明过程自己试着写出来，初步感受一下推理论证。同样在学习到角的有关知识点时，尽管书本没有配套的习题，我自编一题几何说理题：已知，如图2，∠AOB=∠COD，请判断∠AOC 与∠BOD 有怎样的数量关系？为什么？在教学中通过分析，让学生回答证明过程，教师板书如下。

证明：∵∠AOB=∠COD（已知）

∴∠AOB-∠BOC=∠COD-∠BOC（等式性质）

即∠AOC=∠BOD

接着做变式练习：已知，如上图，∠AOC=∠BOD，请判断∠AOB 与∠COD 有怎样的数量关系？为什么？通过讲和练可以让学生自我进行归纳证法：相同线段（或角）±公共部分线段（或角）=新的相同线段（或角），这是为以后的几何学习做好了铺垫工作。事实上，在苏科版七年级（下）学习全等三角形时，经常会利用等式性质去证明线段或角相等的条件，因此，我在这一阶段教学时一直加以重视。

2 重视几何概念教学，逐步感悟几何推理论证

严格的几何推理过程的书写，是从线段的中点概念开始的，因此，在讲解“线段中点定义”时，尤其要重视几何概念的教学，以及几何图形，几何语言的规范书写，这是非常重要的，是学好几何最基本的准备，在教学中我将“线段中点定义”的概念用表格形式列出来，让学生看的更清楚，理解的更深刻。

表1

3 强化几何规范语言的书写，自我实践几何推理论证

在教学中，我发现有些教师对几何语言规范要求的书写不够重视，理由依据也不要求学生写，我认为这种做法对学生学习几何“有百害而无一利”，因为几何规范语言的书写本身是一个难点，如果教师自己不加以重视，那么学生对几何知识的掌握情况就可想而知了。我认为：我们一开始就要求学生规范的书写几何推理过程，并且每一步都要求写出理论依据，教师示范，学生模仿，扎扎实实地进行严格的训练，打好基础，当然开始讲解例题时节奏可以慢一些，好让学生听懂，真正理解。如果我们让学生自己直接写出几何的证明过程，很多学生会感到困难重重，甚至无从下手，这时我们可以出示有填空形式的证明题，例如学填依据训练，教学中要善于引导学生“言必有据”，要让学生理解推理论证的每一步之间都有严密的逻辑顺序关系。

例如1：课本七（下）第9 页练一练2

如图3：（1）如果∠1=∠2，根据______，可得AB∥CE；

（2）如果∠2=∠E，根据______，可得AD∥BE；

（3）如果∠1+∠B=180°，根据______，可得AD∥BE。

图3

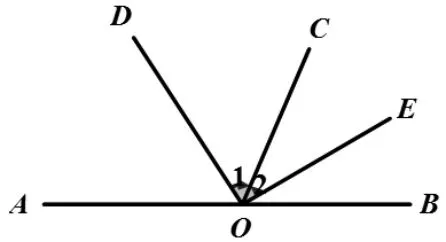
图4

我们还可以让学生进行推理过程的训练，使学生熟悉推理论证的每一步过程，并能明白证明格式的规范要求，作为推理论证的书写样板，由易到难，一步一步地培养学生的推理论证能力。例如七（上）课本第117 页上的一道习题：已知，如图4，∠AOC 和∠BOC 互为邻补角，OD，OE 分别是∠AOC，∠BOC 的平分线。求证：OD⊥OE，我设计成如下的推理填空形式：

证明：∵∠AOC 和∠BOC 互为邻补角（______）

∴∠AOC+∠BOC=（______）

∵OD 是∠AOC 的平分线，OE∠BOC 的平分线（______）

∴∠1+∠2=______+______

即∠______=90°

∴OD⊥OE（______）

4 深化推理论证的基本方法，寻求推理论证的途径

对于七年级学生来说，对几何证明题不知从哪里下手证明的一个主要原因，就是没有掌握推理论证的思考方法。因此，我们在教学中要深化推理论证的基本方法——分析法和综合法的教学，使学生明白分析法：是从所要求证的结论出发，经过研究分析这一结论成立需要具备什么条件，如此逐步向上逆推，一直推到题目的已知条件，可以和学生归纳为：“择果索因”，也就是“拿着结果去寻找原因”。而综合法是从已知条件出发，通过一步步推导，最后推得所要证明的结果，可以简单的概括为：“由因导果”，也就是 “由原因去推导结果”，通过方法的引导，使学生具有一定的解题思路。而在具体解题遇到困难时，还可以将分析法和综合法相结合，我们把它称为“两头凑”的解题方法，事实上在具体解题时非常有用。

例如：已知，如图5，把两个含有45°角的直角三角板如图放置，点D 在BC 上，连结BE、AD，AD 的延长线交BE 于点F.说明：AF⊥BE.

图5

在教学时，我采用分析—综合相结合，引导学生寻求正确的解题途径，具体如下：

分析法：要证：AF⊥BE，即证：∠AFB=90°，

要证：∠AFB=90°，根据三角形内角和定理即证：∠FBD+∠FDB=90°

我们发现：∠FDB=∠ADC（对顶角相等），因此是否能证：∠FBD=∠CAD

因为在Rt△ACD 中，∠CAD+∠ADC=90°而要使∠FBD=∠CAD，必须要证△ACD≌△BCE，引导学生能否找到证全等的3 个条件，由于两个都是等腰直角三角形，可得：AC=BC，CD=EC，∠ACD=∠BCE=90°，从而找到三个条件可证全等.

综合法：∵△ACB 和△DCE 都是等腰直角三角形（已知）

∴AC=BC，CD=EC，∠ACD=∠BCE=90°.

在△ACD 和△BCE 中

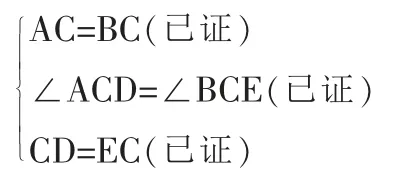
△ACD≌△BCE（SAS）

∴∠FBD=∠CAD（全等三角形的对应角相等）

在Rt△ACD 中，∠CAD+∠ADC=90°

∵∠FDB=∠ADC（对顶角相等）

∴∠FBD+∠FDB=90°

在△BFD 中，∠AFB=180°-（∠FBD+∠FDB）

=180°-90°

=90°

∴AF⊥BE（垂直定义）

5 注重解题思路的引导，切实培养好逻辑推理能力

在学习全等三角形这一章时，有些常规的证明思路方法在教学中要及时跟学生归纳总结，学生在掌握的基础上将更容易的去解决问题，例如：（1）证不在同一个三角形中的两条线段相等时，通常证这两条线段所在的三角形全等；（2）证不在同一个三角形中的两个角相等时，通常证这两个角所在的三角形全等；（3）当不能直接用全等证线段或角相等时，可以转化成证与第三条线段相等或证与第三个角相等的方法来证明；（4）利用全等证某些角相等，从而证明两条直线互相平行；（5）证两条直线互相垂直时，可以和学生归纳为“由已知直角去证未知直角”的方法，中间需要利用全等将某些角进行转化。学生有了这些常规解题的思考方法后，做题时将更得心应手，解决问题的能力也将更强。

同时，我在讲解典型例题后经常要和学生一起反思一下解题的思考方法：

（1）这道题目你是怎么想出来的？

（2）这道题目你怎么想不出来？

（3）这道题目的突破点在哪里？哪个已知条件使你受到了启发;

（4）这种证明思路是否可以推广作为一般方法？有没有其它方法证明这道题目？

（5）做出这道题目后，你对这个知识点的运用是否有更深的理解？等等。

例如：我把课本七（下）第123 页第18 题改编成以下的习题，已知，如图6，在△ABC 中，AB=AC，AD⊥BC，DE⊥AB，DF⊥AC，垂足分别为D，E，F，求证：DE=DF