一种用于差动保护的新型重采样方法

王 业 陆于平 徐以超 许偲轩

（东南大学电气工程学院 南京 210096）

1 引言

近年来，数字化微机保护技术迅速发展，其过程层通常采用电子式互感器（Electronic Current Transducer，ECT），等间隔采样的采样值报文经合并单元（Merging Unit，MU）发送到智能电子设备（Intelligent Electronic Device，IED）进行处理，并以共享的方式通过通信接口提供给二次保护装置[1]。不同数字源采样频率不尽相同，额定采样频率可取为20倍、48倍、80倍工频频率中的任意一种[2]。而传统由电磁式互感器组成的电气测量系统将模拟量送入保护装置，采样在内部进行。以上电气测量系统的变革带来了相应问题。如发电机中性点侧通常是内部自采样，互感器装在发电机套管中，而由于主变压器厂商有可能与发电机厂商不统一及各侧电压等级不一样等原因，主变压器高压侧套管内的互感器有可能与发电机中性点侧互感器采样率不一致，发变组大差动，母差保护及一些后备保护均会存在多数字源采样信号混合输入环境[3,4]，需对采样信号进行重采样。再如ECT往往会集成在气体绝缘组合开关（Gas-Insulated Switchgear，GIS）内部或安装在断路器和变压器套管上，由各自的一次设备制造商供货，因此，在一个数字化变电站中，由于电压等级不一样，可能会出现各个ECT输出数据采样频率并不完全一致的情况，如需实现差动保护需将两侧采样率统一[5]。此外，为提高测量精度和保护特性，IED需将等间隔数据转换成等相角数据，故也需要对IED接口的数据进行重采样[6,7]。

图1给出传统重采样方法[3-11]及本文频域变换重采样方法的流程图，信号首先经过前置模拟低通滤波器，然后在不同采样率A-D采样后进行重采样。对于传统重采样方法，采样率的调整都是在时域进行的，需经过数字低通滤波器来进行抗镜像或抗混叠。文献[5]提出了时域上的抽取插值重采样方法，而信号的抽取和插值各自只能实现信号整数倍采样频率之间的转换，对于分数倍采样频率转换，可将信号的抽取与插值级联，其对于大整数倍和分数倍采样率，滤波器结构非常复杂。文献[3]和[11]提出了时域有限冲激响应滤波器的概念，并以此为基础构造了数字低通滤波器，从电子式互感器输出的离散采样数据恢复出连续信号，重新计算出任意时刻的采样值。对于时域有限冲激响应滤波器，实际上是对输入信号进行两次加窗，通过增加运算量来换取精度的提高。

上述文献提出的重采样方法，如果要达到零相频响应，FIR滤波器延时将达到（N-1）/2[12]（N为插值后一周期点数），故至少延时3～4ms左右，数据才能刚刚符合保护用采样精度，无法满足超高压差动保护快速性的要求[13]，且在采样值差动中，需对每一个时刻的采样值进行差动判别，在连续R次判别中如有S次满足判据，则输出动作信号，而R通常等于或大于N/2（N为一周期采样点数）[14,15]，故采用上述方法其保护输出最小延时为数字低通滤波器延时及连续R次判别的等待时间（复判数据窗延时）之和，总延时将达到半个周期以上，如图2a所示。

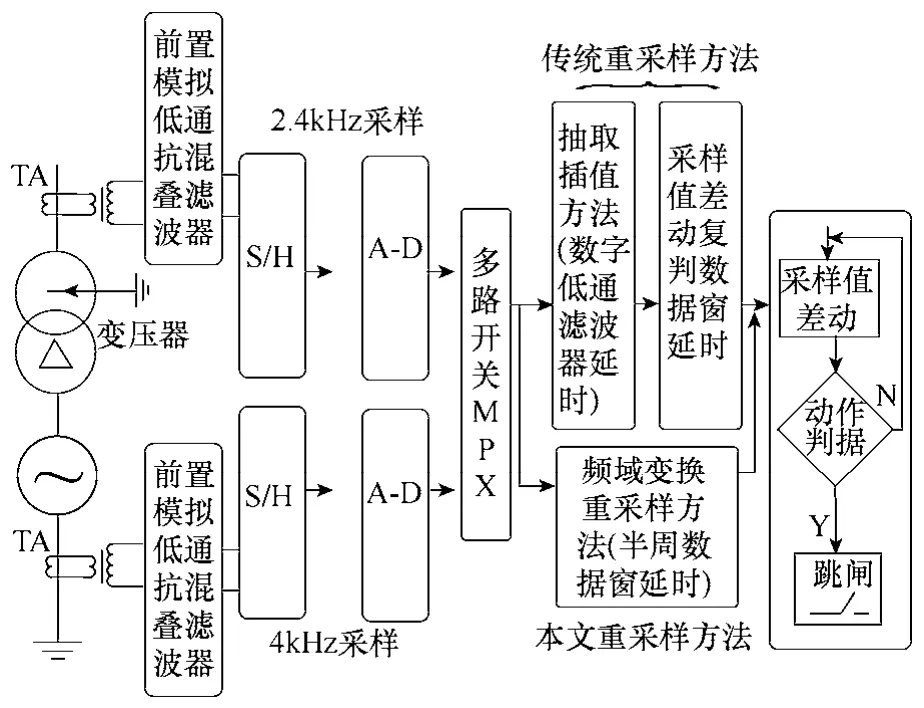
图1 传统重采样及频域变换重采样方法流程图Fig.1 The flow chart of traditional resampling and frequency domain transformation resampling

图2 传统重采样及频域变换重采样方法延时Fig.2 The delay of traditional resampling and frequency domain transformation resampling

综上所述，传统重采样技术已经被国内外许多学者研究得很深入，而差动保护则是系统主保护必不可少的部分[14-18]。为了在保证重采样精度的前提下最大限度地减小重采样延时，可以将采样值差动无法省去的半个周期连续R次判别所用等待时间内的采样数据利用起来以增加重采样精度，本文频域变换重采样方法先对半个周期数据窗的采样值进行半波傅里叶变换，根据重采样要求对其频域进行处理，再反变换到时域，取得信号的瞬时值，无须经过数字低通滤波器。使用本方法，如果采样值差动连续R次判别的复判数据窗为N/2（此处N为一周期采样点数），则在半个周期时，重采样信号已有输出，且保护出口同时也有输出，保护输出总延时为N/2，如图 2b，之后随着数据窗的推移，重采样信号及保护都会逐点输出，且重采样信号输出达到零延时。该方法巧妙地叠加了重采样数据窗及采样值差动保护连续R次判别的复判数据窗，省去时域重采样方法中数字低通滤波器的延时，同时解决了传统时域重采样方法在信号包含高次谐波较丰富时重采样精度较低的问题，提高了重采样精度及减小了重采样延时。

2 频域变换重采样方法

2.1 频域变换升采样

增加采样频率以增加数据的过程称为信号的插值。设原信号为x(n)，采样频率增加L倍，则需在x(n)的两个采样点之间插入 L-1个新的采样点，可以将插入的L-1个采样点的值取为0，同时为了去除插值后的镜像分量，有必要将插零后的信号通过一个数字低通抗镜像滤波器，滤波器的理想特性为[19,20]

其过程如图3所示。

图3 采样信号插值Fig.3 Interpolation of sampling signal

现将该过程在频域上进行推导，分析是否能通过频域上的处理来实现信号升采样。以2倍内插为例，假设插入零后的序列为v(k)，则

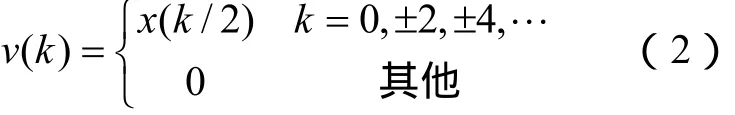
设X(m)为x(n)经半波傅里叶变换后的频谱，即

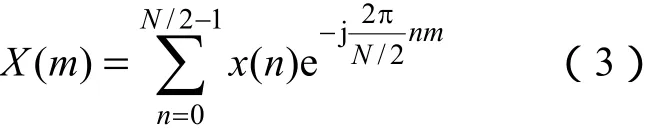
式中，m=0，1，…，N/2-1，N为一周期采样点数（采样点数一般为偶数）。

设V(l)为v(k)经半波傅里叶变换后的频谱，即

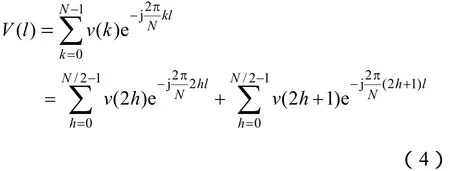
式中，l=0，1，…，N-1。

根据式（2）得

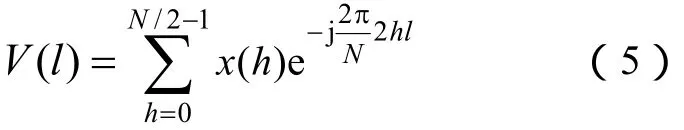
当l≤N/2-1时

当l＞N/2-1时，令l=N/2+s

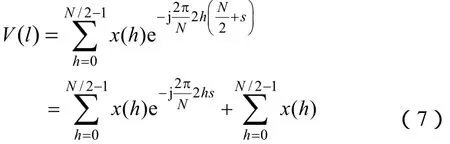
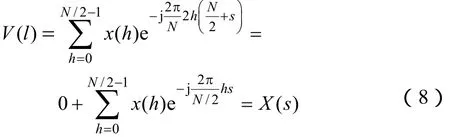
通过以上推导可以看出，插入零值后信号的频谱 V(l)是原频谱的延拓，所以将原信号通过半波傅里叶变换转换为频域序列，并对频域序列按重采样要求进行处理，最后再将处理过的频域序列转换到时域的方法可以对数据进行升采样。而上述式（1）描述的时域上的数字低通滤波则可在本文方法所述频域处理时对原信号频谱进行补零而完成，省去低通滤波器的延时。以上L倍频域变换升采样的步骤为

（1）利用半波傅里叶变换求出原信号 x(n)的频谱X(m)，共N/2点。

（2）对原信号频谱 X(m)进行延拓，补上（LN-N）/2个零，根据重采样率对补零后的频谱进行L倍能量加权，得到V(l)。

需要说明两点：

（1）在原信号频谱 X(m)后面添加零，可以理解为补零的这些信号谱线在原采样信号乃奎斯特频率之上，无法采到这些频率的谱线。

（2）单纯地将信号进行频域变换升采样不需要进行能量加权，但此处升采样的目的是将差动保护两侧不同采样率互感器采得的数据进行采样率统一，进而可以进行差动保护，而由于两侧互感器采样频率不一样，所采得的电流成分存在差别，所以还需根据重采样率对补零后的频谱进行能量加权，使得升采样后的电流成分与另一侧互感器采得的电流成分相同。

（3）对V(l)做NL/2点傅里叶反变换，得到升采样之后的信号y(k)。

2.2 频域变换降采样

降低采样率去除多余数据的过程称为信号的抽取。为了使抽取后的频谱不发生混叠，需要先将原信号经数字低通滤波器（滤波宽度为π/M）对其进行滤波，得到信号 v(n)。数字低通抗混叠滤波器的理想特性为[21,22]

设采样频率降低M倍，则需在v(n)的采样点之间每隔M-1个点抽取一个采样点，形成一个新信号y(k)。其过程如图4所示。

图4 采样信号抽取Fig.4 Decimation of sampling signal

同样将该过程在频域上进行分析，抽取后信号y(k)的频谱 V(l)为抽取前原信号频谱 X(m)经平移以及 M倍展宽后的 M个频谱的叠加和，可以看成升采样的逆过程，限于篇幅，此处不再推导。所以，将原信号 x(n)进行频域变换也可以达到降采样的目的，而上述式（9）描述的时域上的数字低通滤波同样可通过对原信号频谱进行截断而完成，省去低通滤波器的延时，频域变换降采样的步骤为

（1）当（N/2）modM=0时，①利用半波傅里叶变换求出原信号 x(n)的频谱 X(m)，共 N/2点。②对原信号频谱 X(m)进行截断，保留前（N/2）/M个点，根据重采样率对截断后的频谱进行1/M倍能量加权，得到 V(l)。需要说明的是，对原信号频谱进行截断，可以理解为，降采样后信号的乃奎斯特频率变小，其能反映的原信号的频谱范围变小，所以原信号频谱后面的谱线将不再具有意义。③对V(l)做(N/2)/M点傅里叶反变换，得到降采样之后的信号。

（2）当(N/2)modM=a，且 a≠0时，①令N′=M-(N/2)modM；②在原信号后补N′个零，使补零后的信号长度是M的整数倍，并求出此时补零之后信号的频谱X(m)，共N/2+N′个点；③对X(m)进行截断，保留前(N/2+N′)/M 个点，根据重采样率进行1/M倍能量加权，得到V(l)；④对V(l)做(N/2+N′)/M点傅里叶反变换，得到降采样之后的信号。

2.3 频域变换分数倍重采样

对于分数倍重采样，设 i、j互为质数，则 i/j倍重采样实际是 i倍升采样和 j倍降采样的级联，其处理过程如图5所示。

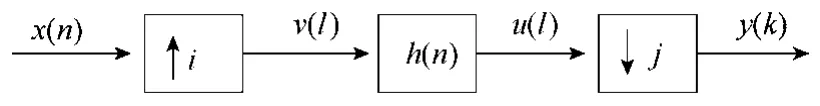
图5 采样信号的插值与抽取Fig.5 Interpolation and decimation of sampling signal

所以，利用频域变换方法对原信号 x(n)进行分数倍重采样的步骤为

（1）当(N/2)modj=0时进行下一步，如果(N/2)modj≠0时，对原信号末端进行补零，求出信号频谱X(m)。

（2）对频谱X(m)的长度进行修正，其长度为i(N/2)/j，并根据重采样率对修正后的频谱进行 i/j倍能量加权。

（3）对新的频谱根据频谱点数进行傅里叶反变换，得到分数倍重采样之后的信号。

针对以上方法，需要说明几点：

（1）此处由于数据窗只有半个周期，故变换出的频谱X(m)将不是真正意义上x(n)的频谱，但由于反变换时的点数也只有半个周期，故反变换后的时域信号依然是准确的。

（2）由于半周期数据窗采样点数较少，造成了采样信号的频谱分辨率降低，即采到的信号最大频率不会改变，但采到的信号中所包含的各个频率成分变少。

（3）传统重采样方法，如时域上的抽取插值法或TCFIR方法，将会由于两侧采样率不一致，致使频谱泄露产生的误差更为严重，在采样率转换误差的基础上进一步引入误差，使得误差率进一步增大，甚至使得差动保护两端较低频率的高频分量增加的误差难以互相抵消，影响到差动保护的运行。而半波频域变换重采样方法，相对时域重采样方法，可以进一步减小误差，因为半波频域变换重采样方法的误差来源主要是由于前置模拟低通滤波器并不可能做到理想状态，高采样率会采得信号较高频率的频谱，而根据采样定律的相关知识，较高频率的频谱会在较低频率的频谱处产生镜像（假频），致使高采样率采得的信号其较低频率的频谱与低采样率采得的信号其较低频率的频谱不一致，使频域变换重采样产生误差。但是通常系统中较高频率的高频信号所占的比重非常小，只占千分之几，故影响不是很大。

3 试验

由于发变组大差动有可能出现保护两侧采样率不一致的情况，故系统模型仿照文献[20]利用Matlab/Simulink搭建了发变组大差动模型，发电机出口电压 13.8kV，500kV两圈升压变采用 Yn/D11接线。试验模型如图6所示，其中CT1的采样频率为 2.4kHz，CT2的采样频率为 4kHz，互感器变比为 1∶1。

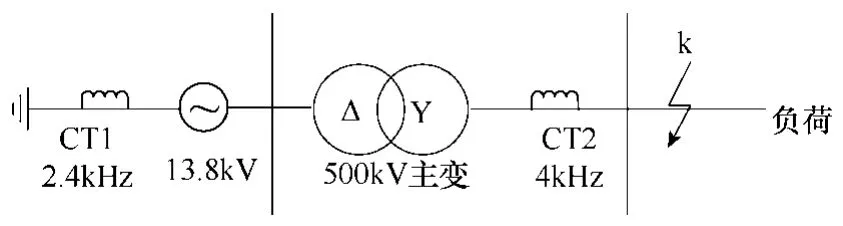
图6 发变组仿真模型Fig.6 The large generator-transformer unit simulation model

需要说明的是：由于本文研究的是用于差动保护的新型重采样方法，故在仿真时应对比计算出重采样之后的数据与重采样前的数据之间的误差为多少，仿真中将CT2采得的采样率为4kHz信号重采样为 2.4kHz信号，并与CT1直接采得的采样率为2.4kHz的信号进行比较，所以应保证重采样前流过CT1与CT2的电流完全一样，这样对比计算出的重采样误差才有意义。故模拟系统正常（电流谐波含量较低）及区外k处单相接地故障切除（电流谐波含量丰富）的情况，对本文提出的方法进行验证。

当两侧信号采样率不一致时，根据奈奎斯特采样定理，两互感器通过的前置模拟低通滤波器截止频率也应不相同。但考虑到试验需比较重采样后的2.4kHz信号与直接以 2.4kHz采样的信号之间的误差，故应保证重采样前两侧信号成分完全相同，所以，此处将两侧信号通过相同的前置模拟低通滤波器，以2.4kHz采样率为基准设计前置模拟低通滤波器，其通带截止频率（0.707处）为380Hz，阻带截止频率（0.01处）为1.2kHz。滤波器频谱特性如图7所示。

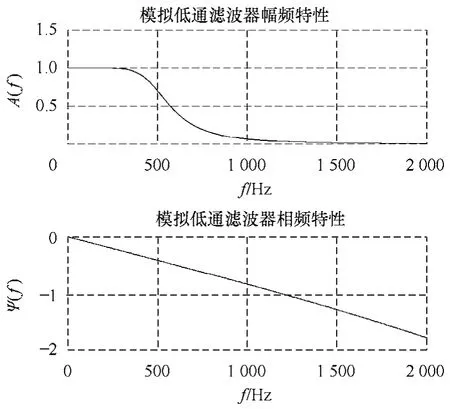
图7 模拟低通滤波器频谱特性Fig.7 Frequency spectrum of low pass filter

（1）当系统未发生故障，正常运行时，此时谐波含量一般，通过全波傅里叶变换分析得到2.4kHz采样与4kHz采样的电流频谱特性如图8所示。

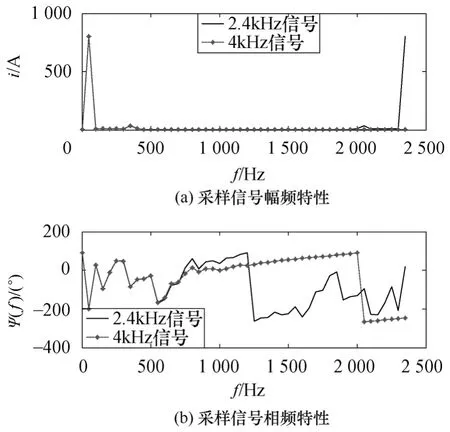
图8 系统正常时采样信号频谱特性Fig.8 Frequency spectrum of sampling signal during normal

由图8可见当系统正常运行时，此时谐波含量很少，谐波总含量为 5.28%，两侧信号的幅频在1.2kHz之前基本一致，以 2.4kHz采样的信号根据采样定理的约束，其频谱（实线）关于1.2kHz对称，1.2kHz以上的频率不能够表示出来，但并不代表其不存在，它将会以假频的形式分散于1.2kHz之前的频谱中，故设计出性能优越的模拟低通滤波器将会提高频域变换重采样的精度，此处由于1.2kHz以上的谐波分量不大，故并不会对误差造成显著影响。而以4kHz采样的信号频谱（点线）则会关于2kHz对称。两侧采样电流波形如图9a所示，频域变换重采样后信号及频谱特性如图 9b～图 9d所示，这里需要说明的是，由于采用半波傅里叶变换，图 9c给出的原2.4kHz信号与重采样后2.4kHz信号的频谱，并不是真正意义上信号的频谱，这里只用于进行对比。

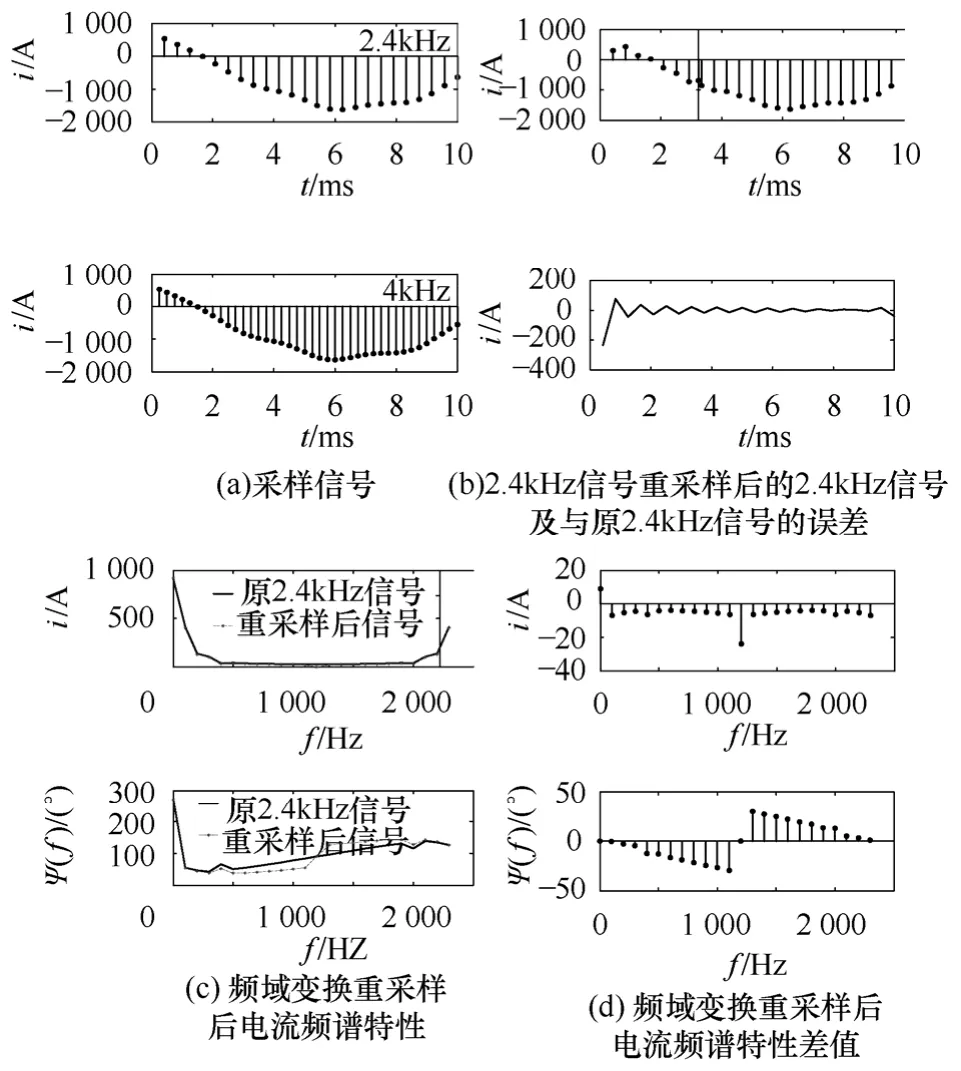
图9 系统正常时频域变换重采样前后信号及频谱特性Fig.9 The original signal,the signal after frequency domain transformation resampling and the frequency spectrum of the signal after frequency transformation domain resampling during normal

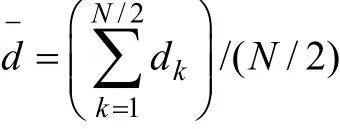
FIR、IIR、TCFIR三种时域重采样方法及频域变换重采样方法产生的误差如图10所示。

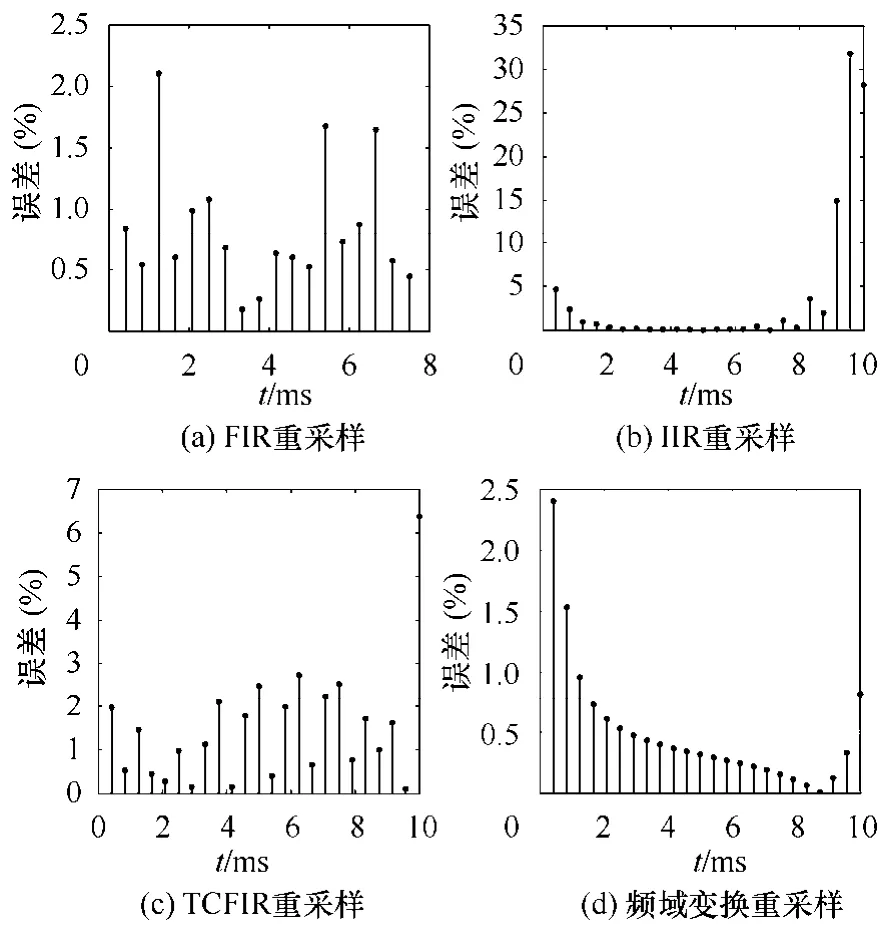
图10 系统正常时FIR、IIR、TCFIR与频域变换重采样误差分析Fig.10 The error analysis of FIR、IIR、TCFIR and frequency transformation domain resampling during normal

分析各种重采样方法的误差率可以看出，FIR采样率转换存在的主要问题是：虽然是线性相位，但在各频率分点都存在一个相位衰减，在时域上表现为信号的群延时。其次，FIR滤波器的通带由于吉布斯效应有较大的纹波，导致重采样误差上下起伏较大。此处将4kHz的采样率转换为2.4kHz的采样率，选取 N=59 ，换算到时域延时为 2.45ms，其瞬时误差基本控制在 1.5%以下，平均误差率为0.83%。基于零相位的IIR滤波器重采样方法，实现了零相位的数字滤波器，使得重采样后的信号没有延时问题。但是，IIR滤波器的拖尾问题是这种方法的一个很大的缺点，最后几个重采样点的瞬时误差很大，最大达到32%，其平均误差率为3.87%。除去最后三个拖尾点后的平均误差率为 0.85%。TCFIR重采样方法选取N=6（此处N与FIR重采样方法中N的意义不一样，详见文献[3]和文献[5]），延时为 2.5ms，由图 10c可知，其瞬时误差基本控制在2%以下，平均误差率为1.49%。频域变换重采样的瞬时误差呈现两边高、中间低的分布，这是由于数据窗的暂态效应引起的，其平均误差率为0.50%，没有延时。可见，频域变换重采样方法不仅没有延时，而且在重采样误差上也远小于前三种时域重采样方法的误差。

（2）当故障点k处发生区外单相接地短路时，电流包含较多的三次谐波，外部故障切除时母线电压恢复，其过程类似空载投入，变压器会因铁心饱和而产生恢复性涌流，此时电流也会包含较多的二次谐波。通过全波傅里叶分析得到的 2.4kHz采样（实线）与 4kHz采样（点线）的电流频谱特性如图11所示，此时，直流分量含量达到6.47%，二次谐波含量达到10.07%，三次谐波含量达到23.36% ，谐波总含量为25.82%，两侧采样电流波形如图12a所示，频域变换重采样后信号及频谱特性如图12b～图 12d所示，同样，图 12c给出的原 2.4kHz信号与重采样后2.4kHz信号的频谱，并不是真正意义上信号的频谱，这里只用于进行对比。

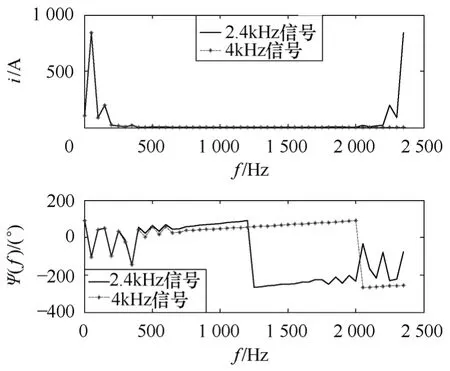
图11 外部故障切除时采样信号频谱特性Fig.11 Frequency spectrum of sampling signal during external fault removal

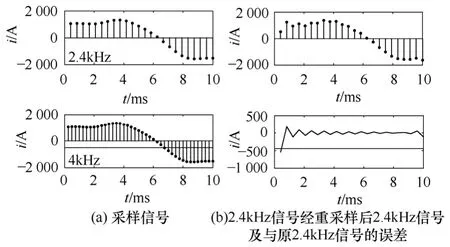
图12 外部故障切除时频域变换重采样前后信号波形及频谱特性Fig.12 The original signal,the signal after frequency domain transformation resampling and the frequency spectrum of the signal after frequency domain transformation resampling during external fault removal

现对此极端状况进行分析，由图12b可见，开始处由于数据窗的暂态效应，差电流达到500A，而实际系统运行时，数据窗是连续的，不会存在此种问题。频域变换重采样后的电流频谱与原 2.4kHz的电流频谱基本重合。现在此极端状况下，分析FIR、IIR、TCFIR三种时域重采样方法与频域变换重采样方法产生的误差，其结果如图13所示。

图13 外部故障切除时FIR,IIR,TCFIR,频域变换重采样误差分析Fig.13 The error analysis of FIR、IIR、TCFIR and frequency transformation domain resampling during external fault removal

分析各种重采样方法的误差可以看出，此处将4kHz的采样率转换为2.4kHz的采样率，FIR重采样（N=59，延时2.45ms）瞬时误差基本控制在2.5%以下，平均误差率为 1.72%。基于零相位的 IIR滤波器重采样方法，最后几个拖尾点最大瞬时误差达到88%，平均误差率为9.49%。除去最后三个拖尾点后的平均误差率为2.20%。TCFIR（N=6，延时为2.5ms）重采样方法瞬时误差基本控制在3%以下，平均误差率为 2.24%。频域变换重采样方法的误差依然呈两边高、中间低的分布，其平均误差率为1.10%，没有延时。

对系统正常运行及在外部故障切除时四种重采样方法的误差率及各自特点进行归纳，具体见下表。前三种时域重采样方法在谐波含量较大时，误差均变得较大，而频域变换重采样误差率依然控制的较低，原因是前三种重采样方法都是在时域进行插值或抽取运算，在原信号由于谐波发生畸变，不再呈某种特定规律变化的情况下，插值或抽取难免会引入较大误差，但频域变换重采样方法通过对频谱的处理进行重采样，原信号无须遵循某种特定规律变化，在将高采样率信号转换为低采样率信号的时候，通过频谱的统一可以将误差率控制得很低，与谐波含量的多少没有太大关系，只是由于前置模拟低通滤波器并不可能做到理想状态，即不可能将高次谐波完全滤去，以4kHz采样的信号中2.4kHz之后的较高频率的高频信号将会映射到2.4kHz之前，造成假频，则重采样之后的信号频谱与直接以 2.4kHz采样的频谱存在细微差别，致使频域变换重采样产生误差。但总的来说，2.4kHz以上的高频分量通常含量都会非常小，最多只占到基波含量的千分之几，所以就算在整体谐波含量相对较丰富时，也不会导致频域变换重采样的误差率增加很多。

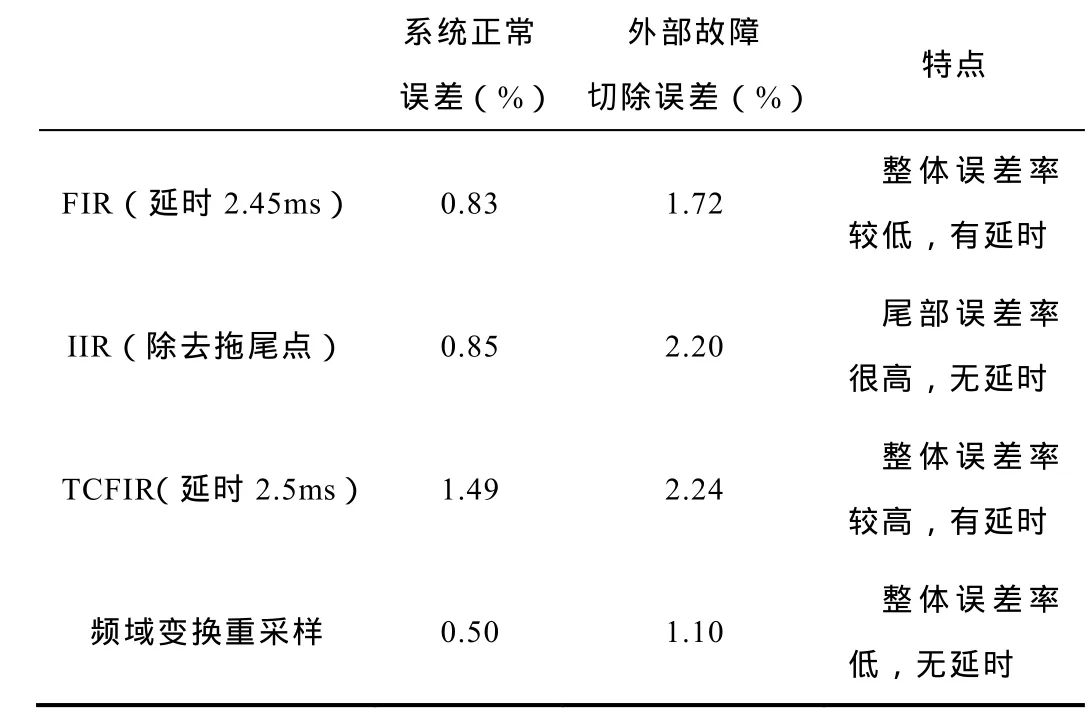
表 FIR，IIR，TCFIR，频域变换重采样误差率对比Tab.The contrast of error of FIR, IIR, TCFIR and frequency transformation domain resampling

4 结论

为了在保证重采样精度的前提下最大限度地减小重采样延时，本文提出频域变换重采样方法。该方法在半个周期时，重采样信号已有输出，且保护同时也有输出，之后随着数据窗的推移，重采样信号及保护都会逐点输出。该方法主要创新点包括：

（1）该方法巧妙叠加重采样数据窗及采样值差动半个周期连续R次判别的复判数据窗，将采样值差动无法省去的复判窗等待时间内的采样数据利用起来以增加重采样精度。

（2）利用频域变换重采样的本质，解决了传统时域重采样在信号包含的高次谐波较丰富时重采样精度较低的问题。

（3）在重采样时，无须将信号经过数字低通滤波器，即省去数字低通滤波器的群延时，最大限度地提高了保护的动作速度，结合第一个创新点，可以让重采样信号输出达到零延时。

仿真验证了新方法在系统正常及外部故障切除时的重采样精度，平均误差率仅分别为 0.50%和1.10%，均优于传统时域重采样方法。

[1]高翔.数字化变电站应用技术[M].北京: 中国电力出版社, 2008.

[2]IEC 60044-8, Instrument transformers: Electronic current transformers[S].

[3]吴崇昊, 陆于平, 徐光福, 等.适用于母线保护的电子互感器采样频率转换算法[J].电力系统自动化,2007, 31(3): 79-82.Wu Chonghao, Lu Yuping, Xu Guangfu, et al.A sampling frequency conversion algorithm of electronic transducer for bus protection[J].Automation of Electric Power Systems, 2007, 31(3): 79-82.

[4]王艳, 张艳霞, 唐俊刺, 等.电力系统广域测量中多采样率转换的研究[J].中国电力, 2010, 43(1):34-37.Wang Yan, Zhang Yanxia, Tang Junci, et al.Study of multi-sample-rate signal conversion in wide area measurement for power system[J].Electric Power,2010, 43(1): 34-37.

[5]徐光福, 陆于平, 吴崇昊, 等.多采样率信号处理在数字化变电站差动保护中的应用[J].电力系统自动化, 2007, 31(21): 44-47.Xu Guangfu, Lu Yuping, Wu Chonghao, et al.Application of multi-rate signal processing in differential protections of digital substations[J].Automation of Electric Power Systems, 2007, 31(21):44-47.

[6]姜永晖, 温渤婴, 丁磊, 等.基于数字化变电站IED接口的数据处理算法[J].电网技术, 2010, 34(2):190-193.Jiang Yonghui, Wen Boying, Ding Lei, et al.Data processing algorithms based on IED interface in digital substation [J].Power System Technology,2010, 34(2): 190-193.

[7]刘益青, 高厚磊, 高伟聪.适用于数字化变电站的继电保护数据处理新方法[J].电力系统自动化,2011, 35(15): 68-72.Liu Yiqing, Gao Houwei, Gao Weicong.A novel data processing approach to relay protection in digital substation [J].Automation of Electric Power Systems,2011, 35(15): 68-72.

[8]Tao Ran, Deng Bing, Zhang Weiqiang, et al.Sampling and sampling rate conversion of band limited signals in the fractional Fourier transform domain[J].IEEE Transactions on Signal Processing,2008, 56(1): 158-171.

[9]Faheem Sheikh, Shahid Masud.Efficient sample rate conversion for multi-Standard software defined radios[J].IEEE Transactions on Signal Processing,2002, 50(4): 854-865.

[10]Djordje Babic, Markku Renfors.Power efficient structure for conversion between arbitrary sampling rates[J].IEEE Signal Processing Letters, 2005, 12(1):1-4.

[11]吴崇昊, 陆于平, 侯喆.基于时域连续有限冲激响应滤波器的电子互感器采样数据站间同步算法[J].中国电机工程学报 , 2006, 26(12): 50-54.Wu Chonghao, Lu Yuping, Hou Zhe.Time-domain continuous FIR filter based electronic instrument transducers sampling data inter-substation synchronization arithmetic[J].Proceedings of the CSEE, 2006,26(12): 50-54.

[12]胡广书.数字信号处理[M].北京: 清华大学出版社,2003.

[13]王维俭.电气主设备继电保护原理与应用[M].2版.北京: 中国电力出版社, 2005.

[14]陈德树, 马天皓, 刘沛, 等.采样值电流差动微机保护的一些问题[J].电力自动化设备, 1996(4):3-8.Chen Deshu, Ma Tianhao, Liu Pei, et al.Problems in realization of microcomputer based differential current protection by sampled values[J].Electric Power Automation Equipments, 1996(4): 3-8.

[15]朱佳杰, 邰能灵.一种发电机差动保护的新方案[J].电工技术学报, 2008, 23(3): 131-136.Zhu Jiajie, Tai Nengling.A novel scheme of generator differential protection[J].Transactions of China Electrotechnical Society, 2008, 23(3): 131-136.

[16]朱国防, 陆于平.扇环型制动区差动保护算法析[J].电工技术学报, 2009, 24(11): 172-177.Zhu Guofang, Lu Yuping.A novel differential protection with sectorring restraint region[J].Transactions of China Electrotechnical Society, 2009,24(11): 172-177.

[17]林湘宁, 刘世明, 杨春明, 等.几种波形对称法变压器差动保护原理的比较研究[J].电工技术学报 ,2001, 16(4): 44-49.Lin Xiangning, Liu Shiming, Yang Chunming, et al.Study on comparisons among some waveform symmetry principle based transformer differential Protection[J].Transactions of China Electrotechnical Society, 2001, 16(4): 44-49.

[18]马静, 王增平.基于标准化网格曲线时频域分析的励磁涌流鉴别新方法[J].电工技术学报, 2007,22(9): 159-166.Ma Jing, Wang Zengping.Analysis of normalized grille curve in time and frequency domains to identify magnetizing inrush[J].Transactions of China Electrotechnical Society, 2007, 22(9): 159-166.

[19]Crochiere R E, Rabiner L R.Interpolation and decimation of digital signals-a tutorial review[J].Proceedings of the IEEE, 1981, 69(3): 300-331.

[20]宗孔德.多抽样率信号处理[M].北京: 清华大学出版社, 1996.