一种频率信号的自适应测量法

刘亚栋 杨洪耕 马 超 刘 张

（四川大学电气信息学院 成都 610065）

1 引言

自从20世纪早期交流电广泛使用开始，电力系统谐波问题就引起了人们的关注[1]。近年来，一方面，电子开关型、电弧型等非线性装置的广泛使用给电力系统带来了大量的谐波、间谐波污染；另一方面，大量敏感设备的使用对于谐波、间谐波的测量与补偿提出了更高的要求[2]。因此，电力系统谐波、间谐波等频率信号的治理是当前一个十分重要的研究领域，而精确地测量出谐波、间谐波是对其进行治理的前提[3,4]。

常规的频率信号测量采用时域-频域的方法[3-8]。这种方法的误差由采样是否同步，采样窗函数性能以及频率分辨率等因素共同决定[8]。随着电力系统中非线性、冲击性负荷的增多，电网频率不能维持50Hz的额定值，而是以其为中心，在较小范围内波动。对于此环境中非稳定谐波、间谐波的测量而言，一方面，需要尽可能高的频率分辨率，另一方面，采样窗口长度要尽量短[8,9]。为此，IEC61000-4-7标准对这种基于频谱分析的频率信号测量方法做出了规范：推荐50Hz系统采样窗口长度为10个基频周波，在此频谱范围内通过谐波、间谐波分组来测量信号各个频率分量。标准是通过对频率分辨率与采样窗口长度两方面要求综合考虑之后才确定出该折中方案[3]，基于此频率分辨率的各种方法在非稳定谐波、间谐波测量中很难得到理想精度的结果[8-11]；标准推荐的利用间谐波组测量间谐波的方法是将两个相邻谐波之间的频谱作为一个间谐波组，从中得到这两个谐波之间间谐波的总体有效值，而无法确定出每一个间谐波分量的准确信息[12,13]。

为此，本文提出了一种能够有效测量电力信号中各频率分量的自适应算法。依据梯度下降法构建出频率信号参数的自适应计算模型，采用李亚普诺夫稳定性定理分析论证了该模型在待测信号非稳定条件下的渐近稳定性，对模型中的参数因子按照动态调节策略进行控制以兼顾自适应测量算法灵敏性和稳定性的要求。

2 频率信号的自适应测量法

2.1 自适应测量算法模型

正弦信号的自适应测量算法就是用预测所得正弦信号去拟合待测信号。在此过程中，根据前面的趋势及误差来预测当前值，再将当前预测值与实测值进行比较以确定新的趋势与误差，直到两者相拟合。这种自适应测量算法能够对幅值、频率及相位随时间变化的非稳定正弦信号进行跟踪测量。

设非稳定信号 u(t)中任一待测正弦频率分量y( t) =A( t) sin （∫ω (τ)dτ + δ(t )），其中 A(t)，ω(t)及δ(t)分别为随时间变化的幅值、角频率以及初相位等信号参数，总相位 φ(t )=∫ω (τ)dτ + δ(t )。要从信号u(t)中检测出该正弦频率分量，就要准确测量出该分量的信号参数，以保证测量所得的输入与输出的差值信号尽可能的小。为此，定义待测频率分量的幅值预测值、角频率预测值ωˆ(t)以及总相位预测值，则可得待测频率分量的预测值为

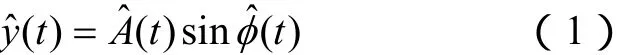
进一步可知测量所得输入与输出的差值信号为

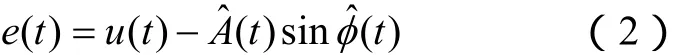
定义目标函数为

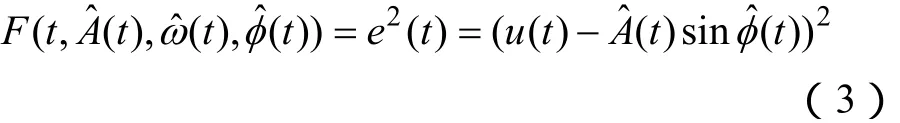
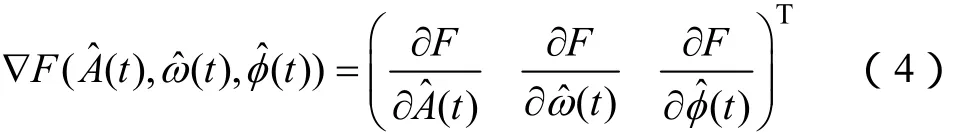
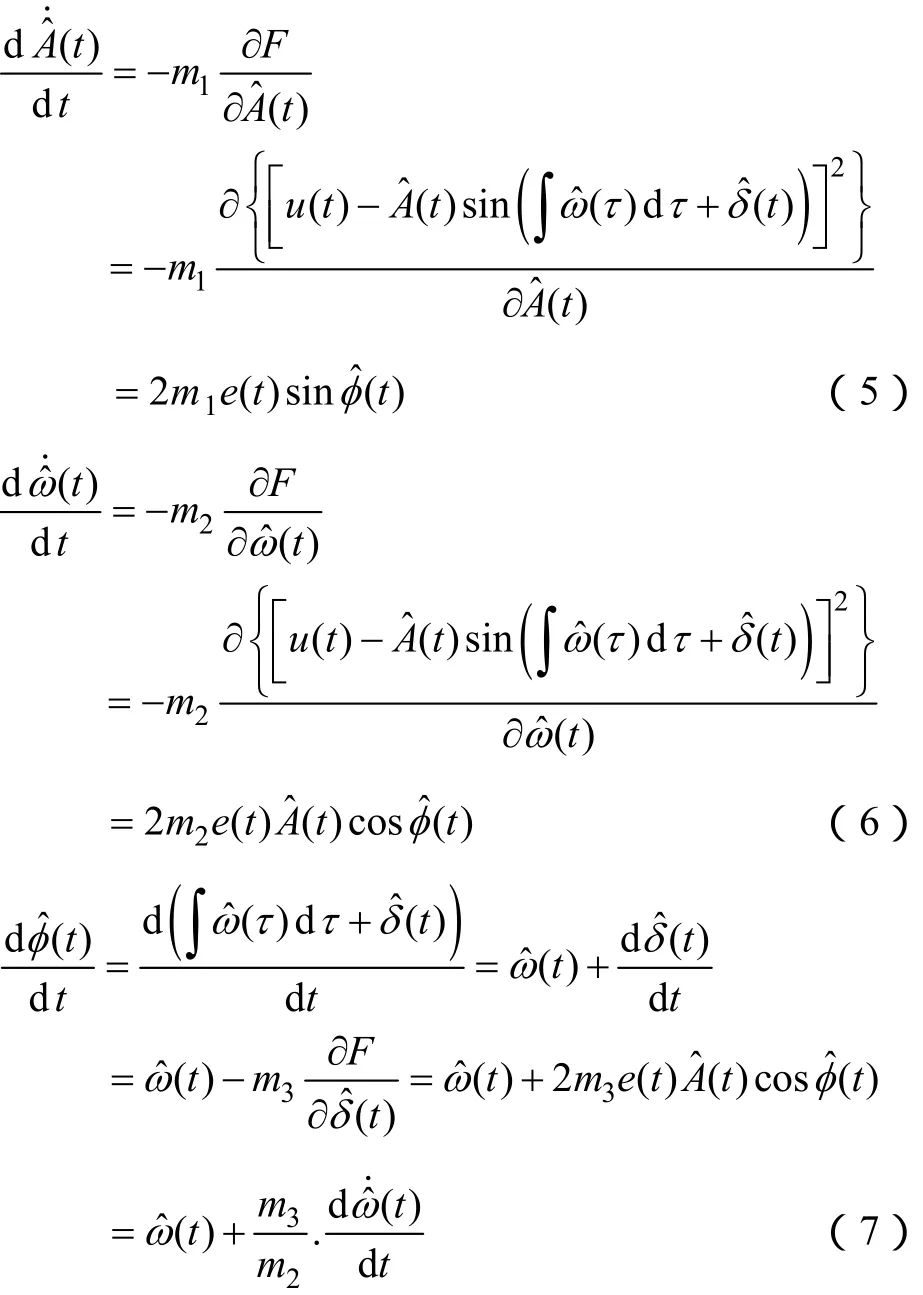
式中，mi(i=1,2,3)为正数。依次定义自适应测量算法的幅值因子Ka、角频率因子Kf及相位因子Kp为：Ka=2m1，Kf=2m2，Kp=m3/m2，则可得如下3阶动态系统所示的自适应测量算法模型，其状态变量分别为幅值预测值、角频率预测值ωˆ(t)及总相位预测值。

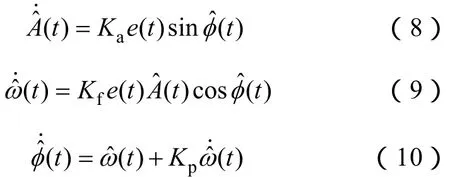
在具体软件计算中，对式（2）及式（8）～式（10）进行离散化处理，则有

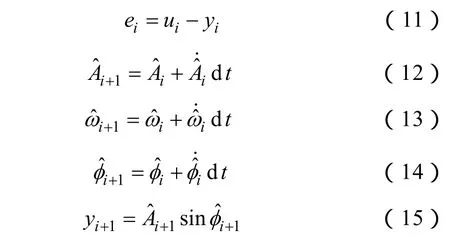
在式（8）～式（10）所示的自适应测量算法模型中，参数因子Ka, Kf及Kp用来控制算法的收敛速度与稳态误差。只要为该算法设置角频率初始值ω0以及上述 3个参数因子，就能保证预测信号与输入信号中角频率最接近于ω0的频率分量相拟合。

2.2 自适应测量算法的稳定收敛性

在 2.1节中给出的频率信号自适应测量算法模型是一个非线性系统，其稳定收敛性往往通过该系统的平衡点或周期解的稳定性来分析。在此，依据李亚普诺夫稳定性定理对该系统平衡点的稳定性进行分析。

假定信号u(t)为有界连续的周期信号，根据傅里叶级数，同时考虑到信号参数可能随时间在较小范围内变化，可以将其写成

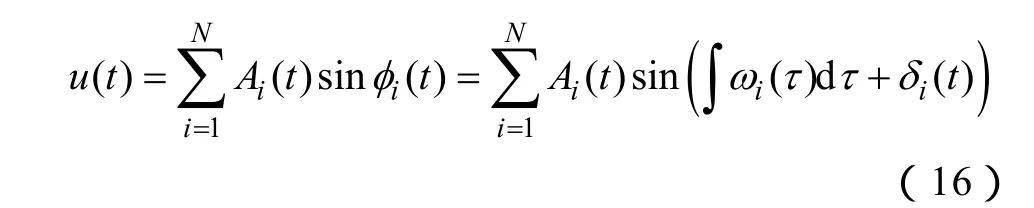
式中，N为u(t)中所含频率分量的个数；Ai(t)、ωi(t)及 δi(t)分别为随时间变化的第 i个频率分量的幅值、角频率及初相。为便于分析，依据文献[14]中的平均理论对u(t)进行线性平滑近似后可得

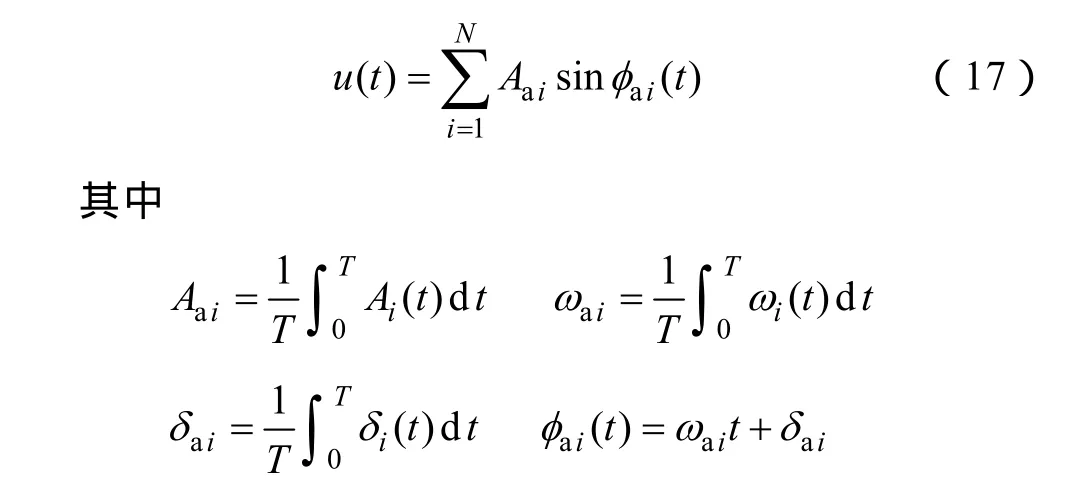
T为信号周期。则由式（2）及式（17）可得

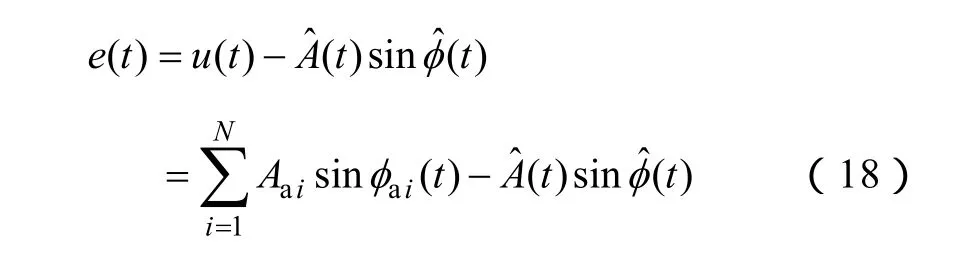
对式（18）左右两端关于时间求微分，并将式（8）～式（10）代入可得

以测量u(t)中第k个频率分量为例，则其他频率分量之和即为输入与输出的差值信号 e(t)。在平衡点附近近似有：据此对式（19）进行简化后根据文献[14]中的平均理论可得

2.3 电力频率信号的自适应测量法

考虑到电力频率信号中除含有基波，通常还包含少量的谐波（整次或非整次）及噪声信号。要想分析电力信号中的各个频率分量，就需要将多个根据 2.1节中算法构成的自适应测量单元按照一定的结构组合起来，同时根据对输入信号进行FFT预处理所得的频谱范围针对性地设置每个测量单元的角频率初始值ω0，以保证对于输入信号中任一频率分量都有唯一的自适应测量单位对其进行快速准确的拟合。图1给出了自适应测量单元的两种组合结构。

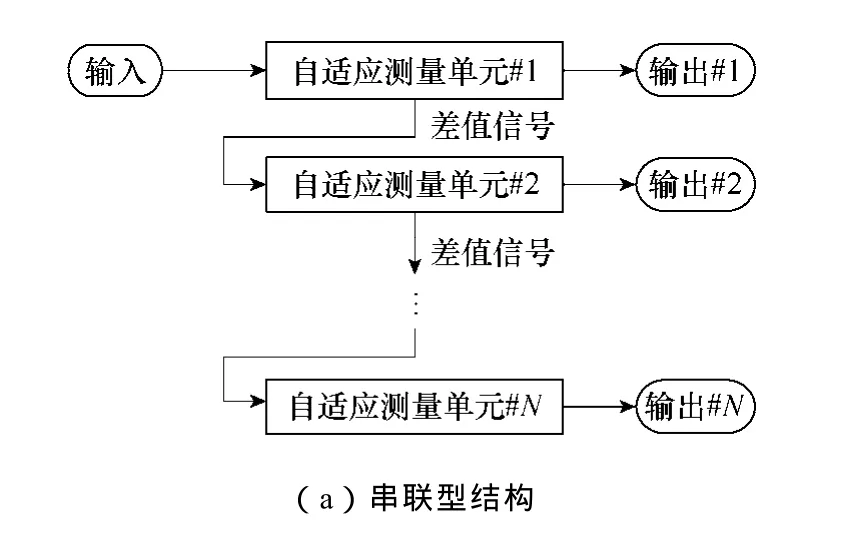
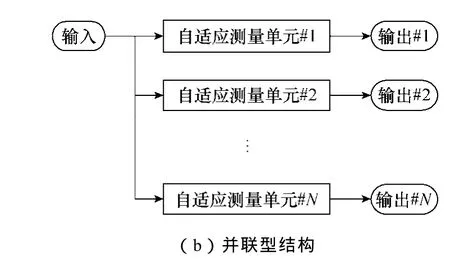
图1 自适应测量结构Fig.1 Block diagram of adaptive measurement

图1所示的两种结构均能实现对输入信号中各个频率分量的测量。在串联型结构中，每个单元将上一个单元输入与输出的差值信号作为输入，考虑到电力频率信号中次数越高的谐波，含量越小，这种结构可以逐次剔除检测出的低次谐波分量，准确地测量出含量较小的频率分量。并联型结构中的各个单元同时对输入信号中相应的频率分量进行自适应测量，具有较高的效率。在实际应用中可根据需要灵活选用这两种结构。本文仿真实验中采用串联型结构对算法进行验证。

3 自适应测量法的动态参数因子调节策略

3.1 自适应测量算法的参数因子特性

注意到 2.2节中关于自适应测量算法稳定收敛特性的证明是一个局部证明，必须合理选取参数因子 Ka, Kf与 Kp以及角频率初始值 ω0才能保证算法准确快速收敛于输入信号中的待测频率分量。由式（8）～式（10）可知，算法中 Ka主要控制信号幅值的收敛速度及稳态计算误差，Kf及Kp主要控制频率和相位的相应特性。进一步由式可得，上述参数因子取值较大时算法收敛速度较快，但是当信号畸变严重时，即使预测信号逼近待测频率分量，测量所得输入与输出的差值信号 e(t)仍较大，此时，较大的参数因子将进一步增大信号参数随时间变化率的计算值，从而在测量结果中产生较大的稳态误差；参数因子取值较小时，各测量单元能够精确检测出待测频率分量，但不能及时跟踪信号参数的快速波动，动态响应速度较慢。

3.2 动态参数因子调节策略

电力频率信号的测量算法在理想情况下应该满足以下要求，当待测信号的幅值、频率或相位发生变化时能迅速做出反应，并快速收敛到新的稳定状态，具有较强的灵敏性；当待测信号比较稳定时能有效抑制干扰，准确收敛到待测信号，表现出较好的稳定性。

根据 3.1节中对自适应测量算法参数因子特性的分析，要满足上述测量要求，常规的思路是综合算法灵敏性和稳定性两方面要求，折中地设置参数因子值[15]。目前看来，这种做法并不是理想的解决方案，采用时变参数因子能够取得更理想的测量精度和速度[16]。因此，在本算法中，将自适应计算过程中提供的某些回馈量作为衡量标准来调节参数因子，在计算初始阶段或者信号参数跳变时，参数因子取值相对大一些，以便有较快的收敛速度；计算值逼近待测值时，参数因子取值相应地减小一些，以保证算法准确收敛于待测频率信号。

由于输入信号畸变严重时，每个测量单元输入与输出的差值信号 e(t)并不能有效反映信号分量预测值与待测值逼近的真实情况，而本算法中以各信号参数测量误差的变化趋势为依据，动态调节相应的参数因子。由数学知识可知，任意函数的一阶导数能够反应该函数的变化趋势，导数值越大说明函数值变化越剧烈。在离散计算情况下，用差分代替微分，分别以幅值、频率及相位测量误差的差分值作为回馈值，对相应的参数因子进行调节。由式（10）中频率与相位的相关性可知，参数因子 Kf与 Kp均与相位正相关，单独调节 Kf或者 Kp对相位的计算均有效。因此，为简化计算过程，本算法中只对幅值因子Ka及频率因子Kf进行动态调节。

从算法的收敛速度及稳态误差两方面考虑，在计算过程中，对参数因子作如下限制

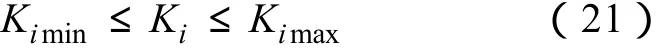
式中，i=a, f，0＜Kimin＜Kimax。选择 Kimax时主要考虑信号畸变较严重时算法的稳态误差，Kimin的选择需要综合算法的收敛速度及稳态误差后取一个折中值。具体的参数因子动态调节策略如下式所示。

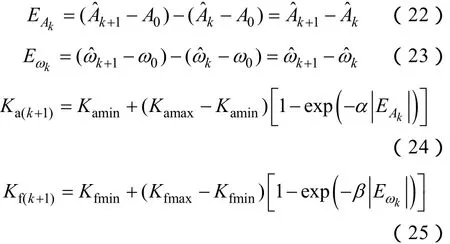
式中，A0、ω0分别为幅值与角频率的待测值；α、β为正常数。在计算过程中，分别根据幅值测量误差与角频率测量误差的变化趋势调节相应的参数因子。以幅值因子为例，在计算初始时刻或者信号幅值跳变时刻，EAk较大，幅值因子取值接近 Kamax，算法具有较快的幅值收敛速度；反之，当幅值测量值逼近待测值时，幅值因子取值接近Kamin，从而有效防止了稳态失调。

4 仿真分析

在 Matlab7.1仿真环境下，首先取多个畸变较严重的输入信号，对每一个输入信号，分别为幅值因子 Ka、频率因子 Kf以及相位因子 Kp取多组不同的值，在不同的固定参数因子条件下进行多次实验。从中选取几次典型的信号幅值测量结果，通过对比分析，从这几次实验所设置的幅值因子值确定出本文仿真实验中幅值因子的取值范围 Kamax及 Kamin。同样地，根据多次频率测量实验结果确定出本文仿真实验中的Kfmax以及Kfmin。确定了Ka与Kf之后继续在不同的相位因子Kp条件下进行多次实验，从中选择几次典型测量结果，进而确定出Kp的一个合理取值范围，选取该范围的中间值作为本文仿真实验中Kp的固定取值。确定了Ka、Kf的范围以及Kp的值之后，设置不同的正常数α、β，根据式（24）和式（25）在信号幅值及频率跳变情况下对上述几个畸变较严重的输入信号分别进行多次实验，通过对比分析，从中选取能够在尽可能短的动态过程后准确收敛到信号参数跳变后新状态的正常数作为本文仿真实验中α，β 的值。由于本文仿真算例中的参数因子范围或取值是预先通过对不同的信号进行大量实验对比分析确定的，因而这些取值具有一定的普适性。

下面在输入信号幅值跳变、基波频率跳变、基频频率连续波动以及其中存在间谐波分量等几种典型情况下对本文方法进行仿真验证。为了凸显本文方法在稳定性与灵敏性方面的优势，还将在信号幅值跳变以及基波频率跳变两种信号参数快速波动场合下对采用动态参数因子调节策略的本文方法及常规的折中设置固定参数因子的方法进行实验对比。在这里，折中设置的Ka与Kf分别取为Kamax、Kamin及 Kfmax、Kfmin的均值，两种方法中相位因子 Kp的取值相同。

4.1 幅值跳变的谐波信号分析

设仿真所用的负载电流频率信号i(t)为

式中，基频额定频率 ƒ0=50Hz；δ1、δ2及 δ3为任意常数；采样频率ƒs=10kHz。

算法中相关参数的取值如下：Kamax=200，Kamin=100，Kfmax=9 000，Kfmin= 7 000，Kp=0.15，α=1.5，β=3.5。假设在t=0.2s时，信号i(t)中各个频率分量的幅值变为原值的0.8倍，在t=0.4s时又恢复原值。根据FFT预处理所得的频谱范围设置各个自适应测量单元的ω0值依次为 100π、500π、1 400π及 2 200π。限于篇幅，在此只从仿真结果中选择具有代表性的波形及幅值/频率测量曲线来说明本文方法的有效性。图2所示为信号i(t)及从中检测出的基频分量，图3为测量到的7次谐波幅值及相应的幅值因子曲线。由图可见，无论在信号幅值稳定还是非稳定条件下，本文方法均能准确跟踪信号幅值，快速收敛到待测频率分量；通过对比分析图3a中采用动态参数因子调节策略的本文方法与固定参数因子方法的测量曲线，可以发现，本文方法在信号幅值跳变后1个基波周期内就能准确收敛到新的稳定值，动态过渡过程更短，具有更高的测量速度，而且不存在明显的稳态测量误差，与理论分析的结果一致。

图2 幅值跳变情况下自适应测量法的仿真结果Fig.2 Simulation result of adaptive measuring method when the amplitudes undergo step change

图3 7次谐波分量的幅值及幅值因子曲线Fig.3 Amplitude and its factor curves of the 7th harmonic component

4.2 基频频率跳变的谐波信号分析

负载电流频率信号与 4.1节中的 i(t)相同，采样频率ƒs=10kHz。算法中相关参数的选取以及各个自适应测量单元的ω0也与上例一致。假设在 t=0.2s时信号i(t)的基频频率变为50.5Hz，在t=0.4s时频率又恢复到额定值。图 4中给出了 i(t)及从中检测出的基频分量波形，图5a中给出了用本文方法与折中设置固定参数因子的方法检测到的5次谐波幅值曲线，图5b为本文方法中相应的幅值因子曲线，图6a给出了两种方法测量得到的基频频率，图 6b为本文方法中相应的频率因子曲线。结合图 5及图6可见：在基频频率跳变情形下，本文方法仍能快速准确收敛到待测的各频率分量，跟踪测量各分量的幅值及频率随时间的变化；相对于折中选取固定参数因子的方法，动态参数因子调节策略保证了本文方法在信号频率跳变后更短过渡过程内就能准确收敛到信号新的稳定值，而且未出现明显的稳态误差，进一步证实了理论分析。

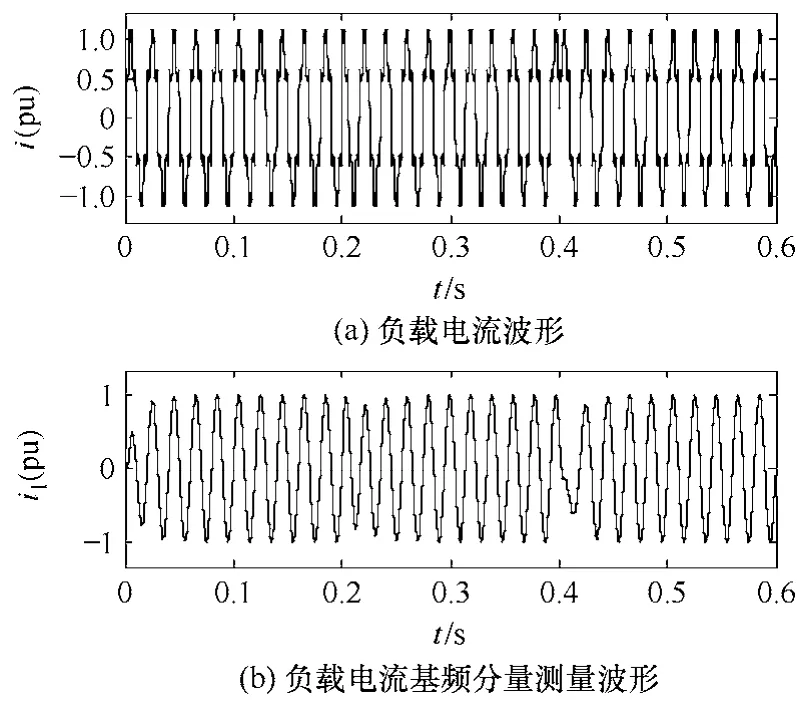
图4 频率跳变情况下自适应测量法的仿真结果Fig.4 Simulation results of adaptive measuring method when the fundamental frequency undergoes a step change

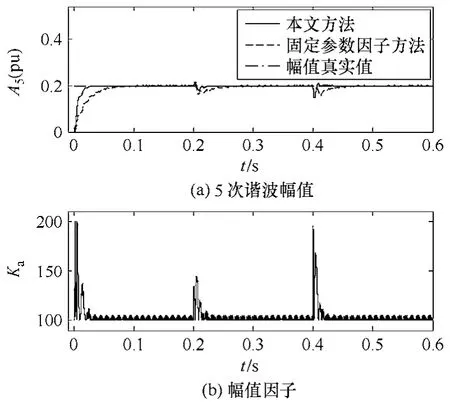
图5 5次谐波幅值及幅值因子曲线Fig.5 Amplitude and its factor curves of 5th harmonic component

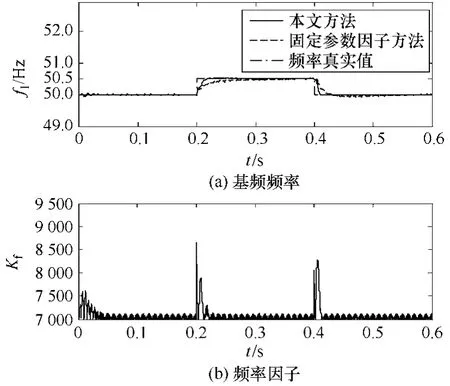
图6 基频频率及频率因子曲线Fig.6 Frequency and its factor curves of fundamental component

4.3 基频频率随时间波动的跟踪分析

考虑到实际电力系统中，电网基波频率通常在较小的范围内连续波动，为此，进一步对本文方法跟踪测量频率信号的能力进行检验。假设 4.1节中负载电流信号i(t)的基频频率f0=50+0.5sin(2πt)，即基频频率在0.5Hz的范围内正弦波动。则对于本文方法，依次设置各个自适应测量单元的角频率初始值ω0以及算法中的相关参数与4.2节中相同，对输入信号中各个频率分量进行跟踪测量。图7中给出了基频频率跟踪曲线。对比分析图中的两条频率曲线，不难发现，当基波频率在较小范围内连续波动时，本文方法能够在较短的动态过程之后实现对信号频率的准确跟踪测量，具有较理想的动态测量速度及稳态测量精度。

图7 随时间波动的基频频率Fig.7 Fluctuations of fundamental frequency with time

4.4 间谐波信号分量分析

假设输入频率信号中除了 4.1节中 i(t)所包含的各次谐波分量，还包含频率为68Hz及83Hz的间谐波分量，其幅值分别为0.1(pu)及0.08(pu)。此外，为检验本文方法在噪声环境下的性能，向输入信号中加入高斯白噪声以得到信噪比（Signal Noise Ratio，SNR）为20dB的信号。通过对输入信号取10个周波进行FFT预处理后确定各频率分量的大致频谱范围，据此设置的对应于两个间谐波分量的自适应测量单元的角频率初始值ω0分别为140π及160π。图7和图8中分别给出了测量所得的两个间谐波分量的幅值及频率曲线。为进一步提高测量精度，在这里，Ka及Kf的初始值较4.1节中均相对减小，故收敛速度相对较慢。由图可见，本文方法在信号畸变较严重的情况下能够有效抑制其他频率分量及噪声的影响，准确收敛到待测频率分量，与理论分析结果一致。

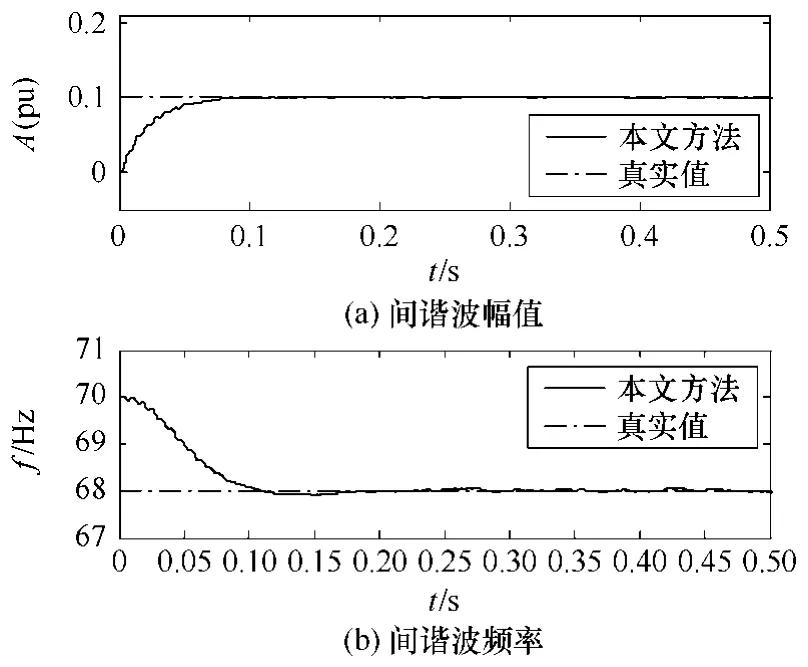
图8 频率为68Hz间谐波的幅值与频率Fig.8 Amplitude and frequency curves of inter-harmonic with 68Hz for frequency

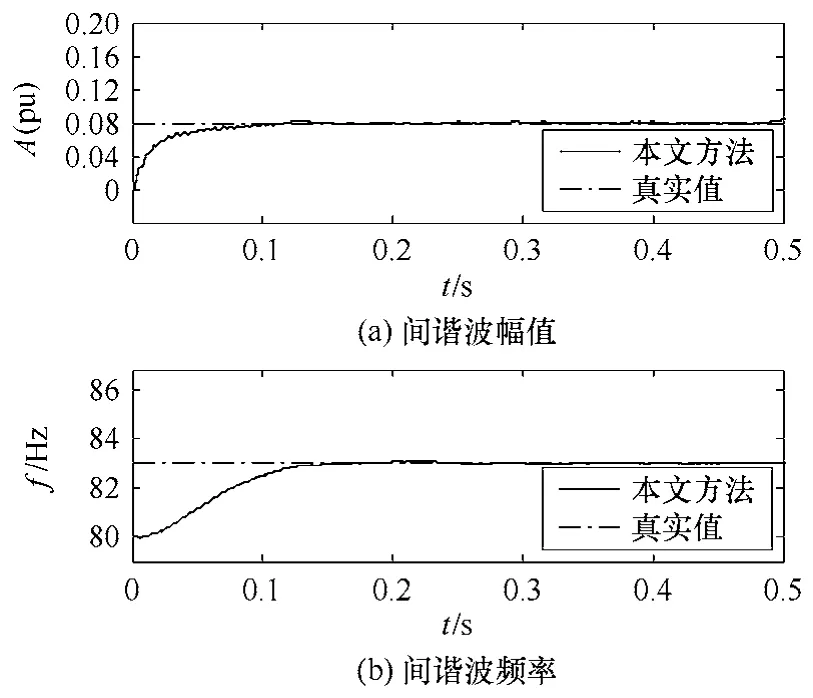
图9 频率为83Hz间谐波的幅值与频率Fig.9 Amplitude and frequency curves of inter-harmonic with 83Hz for frequency

5 结论

（1）提出的自适应测量法能够准确测量出输入频率信号中各个频率的谐波、间谐波分量。

（2）在频率信号稳定和非稳定条件下，李亚普诺夫稳定性定理均能保证该自适应测量法渐近稳定地收敛到输入信号中各个待测的频率分量。

（3）动态参数因子调节策略的采用能够兼顾算法的动态响应速度和稳态测量误差两方面要求，保证算法的灵敏性和稳定性。

[1]Lin H C.Inter-harmonic identification using group-harmonic weighting approach based on the FFT[J].IEEE Transaction on Power Electronics, 2008,23(3): 1309-1319.

[2]Clark S L, Famouri P, Cooley W L.Elimination of supply harmonics[J].IEEE Industry Applications Magazine, 1997, 3(2): 62-67.

[3]Apuzzo M D, Arco M D.A time-domain approach for the analysis of nonstationary signals in power systems[J].IEEE Transaction on Power Delivery,2008, 57(9): 1969-1977.

[4]蔡涛, 段善旭, 刘方瑞.基于实值MUSIC算法的电力谐波分析方法[J].电工技术学报, 2009, 24(12):149-155.Cai Tao, Duan Shanxu, Liu Fangrui.Power system analysis based on real-valued spectral MUSIC algorithm[J].Transactions of China Electrotechnical Society, 2009, 24(12): 149-155.

[5]赵黎丽.基于相关 Hanning窗插值的间谐波分析算法[J].电工技术学报, 2008, 23(11): 153-158.Zhao Lili.Inter-harmonics analysis based on correlation hanning window and interpolation algorithm[J].Transactions of China Electrotechnical Society, 2008, 23(11): 153-158.

[6]曾博, 滕召胜.纳托尔窗改进 FFT动态谐波参数估计方法[J].中国电机工程学报, 2010, 30(1): 65-71.Zeng Bo, Teng Zhaosheng.Improved FFT approach for the dynamic state estimation of harmonic parameters based on the Nuttall window[J].Proceeding of the CSEE, 2010, 30(1): 65-71.

[7]吕干云, 方奇品, 蔡秀珊.一种基于粒子群优化算法的的间谐波分析方法[J].电工技术学报, 2009,24(12): 156-161.Lv Ganyun, Fang Qipin, Cai Xiushan.A method for inter-harmonics analysis based on PSO[J].Transactions of China Electrotechnical Society, 2009,24(12): 156-161.

[8]Aiello M, Cataliotti A, Nuccio S.A comparison of spectrum estimation technique for nonstationary signals in induction motor drive measurements[J].IEEE Transaction on Instrumentation and Measurement,2005, 54(6): 2264-2271.

[9]陈涵, 刘会金, 李大路, 等.非均匀采样和最小二乘法在间谐波检测中的应用[J].中国电机工程学报,2009, 29(10): 109-114.Chen Han, Liu Huijing, Li Dalu, et al.Application of nonuniformly sampling and least square technique in inter-harmonic measurement[J].Proceeding of the CSEE, 2009, 29(10): 109-114.

[10]Aiello M, Cataliotti A, Nuccio S.A chirp-z transform-based synchronizer for power system measurements[J].IEEE Transaction on Instrumentation and Measurement, 2005, 54(3): 1025-1032.

[11]Kusljevic M D.Simultaneous frequency and harmonic magnitude estimation using decoupled modules and multirate sampling[J].IEEE Transaction on Instrumentation and Measurement, 2010, 59(4): 954-962.

[12]IEC61000-4-7, General guide on harmonics and inter-harmonics measurements and instrumentation,for power supply systems and equipment connected thereto[S].

[13]Bracale A, Carpinelli G, Lauria D, et al.On some spectrum estimation methods for analysis of nonstationary signals in power systems[C].Proceeding of 11th International Conference on Harmonics and Quality of Power, 2004: 260-265.

[14]Guckenheimer J, Holmes P.Nonlinear oscillations,dynamical systems, and bifurcations of vector fields[M].New York: Springer-Verlag, 1991.

[15]Tey L H, So P L, Chu Y C.Improvement of power quality using adaptive shunt active filter[J].IEEE Transaction on Power Delivery, 2005, 20(2):1558-1568.

[16]李辉, 李亦斌, 邹云屏, 等.一种新的变步长自适应谐波检测算法[J].电力系统自动化, 2005, 29(2):69-73.Li Hui, Li Yibin, Zou Yunping, et al.A novel adaptive harmonic detecting algorithm based on variable step-size LMS[J].Automation of Electric Power Systems, 2005, 29(2): 69-73.