计及节点恢复成功率的黑启动分区恢复方案优化

梁海平 郝 杰 顾雪平

（华北电力大学电气与电子工程学院 保定 071003）

1 引言

互联电网发生大停电事故后，制定合理的分区并行恢复策略对于加快系统的恢复进程，减少大停电事故带来的经济损失具有重要的现实意义。目前关于电网分区并行恢复策略的研究主要集中在如何在分区内部建立恢复网架，涉及如何分区问题的文献，主要有以下几种研究方法。

文献[1]通过主干网把黑启动电源、待启动机组节点以及重要负荷节点连接成一个网络，根据设定的约束条件进行合理解列，解列得到的子网就是黑启动分区结果。该算法将黑启动分区问题转化为满足一定约束条件下确定电网中所有线路的通断问题，没有对分区内机组的启动顺序进行合理考虑，也没有考虑机组的启动时间限制。文献[2]定义了网络社团的模块度指标和输电线路的边介数，通过GN分裂算法，不断从网络中移除边介数最大的边，将原来连通的网络划分为几个子系统，然后通过计算各个子系统的模块度指标来对结果进行调整和优化。文献[3]考虑输电线路的线路长度、电压转化次数、中间电站个数三个方面对恢复路径进行评价赋值，将网络形成一个赋权网络，以各子系统中的所有节点到各自区域黑启动电源的路径长度之和作为禁忌搜索算法的目标函数，但没有考虑发电机的恢复状态和启动时间限制。文献[4]提出了计及火电机组启动过程的网架并行恢复策略，建立了机组累积启动时间与机组停机之间的关系，并用Prim算法优化送电路径；文献[5-7]采用了基于遗传算法的黑启动分区策略，综合考虑机组的启动特性和系统的恢复状态，设定分区优化目标函数，应用遗传算法进行优化问题的求解，其不仅可以得到节点所属的分区，同时也可以得到分区内部线路的投运次序。文献[8, 9]考虑机组的启动时限，采用最短路径法寻找恢复过程中的最优路径。

以上各种分区策略中，均没有考虑输电线路投运的不确定性以及送电路径操作灵活性的差异。实际的电力系统中，由于输电线路的运行环境、故障排除状态以及本身所在网络中的位置不同，其投运成功与否，存在一定的不确定性。同一个目标节点，选择不同的恢复路径，其能够得到成功恢复的概率是不一样的；同一个黑启动电源点，恢复不同的目标节点，其恢复成功的概率也是不一样的。

针对以往研究所存在的问题，本文提出一种计及节点恢复成功率的黑启动分区优化策略。首先，根据目标节点到达不同黑启动分区恢复路径的情况，应用图论中依据最小路集计算系统正常工作概率的方法，计算出该节点由指定分区恢复成功的概率，同时综合考虑路径的恢复时间，设定了分区判定函数来确定节点所属最优分区。其次，对于已经确定所属分区的某个目标节点，考虑到恢复时间的紧迫性，对分区内部恢复该节点的送电路径进行优化，同时，结合路径的恢复用时以及机组动态恢复模型，可以确定机组节点的启动状态，从而求解出其后续恢复过程中的出力。最后，本文提取了分区子系统网络重构效率指标、分区恢复的时间耗费指标以及各分区恢复用时方差指标建立了分区优化目标函数，并应用交叉粒子群算法实现电网分区优化问题的求解。

2 基于最小路集的节点恢复成功率的求解

2.1 最小路集相关概念

图是节点和边的集合，记为G={V, E}，其中V为节点，E为边。若连接节点之间的边是有方向的，称为有向边；若连接两个节点之间的边是无向的，称为无向边。由无向边构成的图称为无向图；由有向边构成的图称为有向图；既含有有向边又含有无向边的图成为混合图。

路集是指连接任意两个节点间有向边或无向边组成的边的集合。如果一条路中移去任意一条边后就不再构成路，则这条路成为最小路。由最小路构成的集合称为最小路集[10]。

2.2 求解网络最小路集的方法

求解网络的最小路集的方法有联络矩阵法、布尔行列法以及搜索法。本文采用搜索法求解复杂网络的最小路集。搜索法的基本思想是由网络的起始节点作为根节点开始依次向目标节点搜索，找出全部最小路。利用搜索树的方法可以使得搜索过程变得条理清晰、简单可用。如图1为一个简单的混合图。

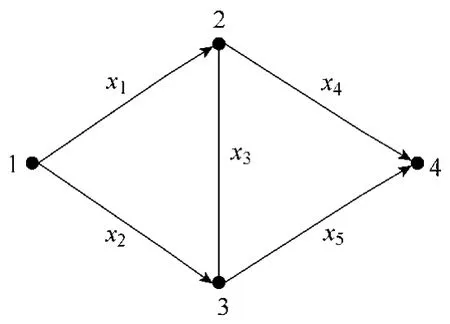
图1 点弧图Fig.1 Node arc graph

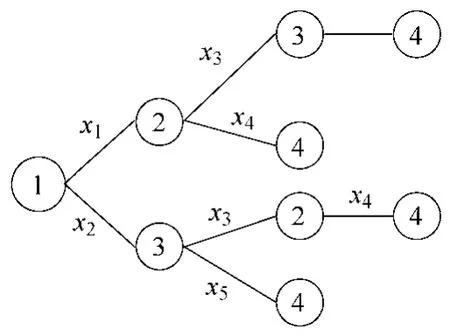
图2 搜索树Fig.2 The searching tree

选择1节点为树根作搜索树，搜索到达4节点的所有最小路。搜索树如图2所示。由搜索树的结果可知，最小路集为：[x1x4,x2x5,x1x3x5,x2x3x4]。

2.3 由最小路集求系统可靠工作的概率

一般求得的最小路是相交的，或者说是相容的。需要首先把相交的最小路先化为不相交的最小路，然后求解系统的工作概率，这一过程称为不交化过程。这里采用“删去留下”算法对最小路集进行不交化变换。

“删去留下”算法的步骤如下：

（1）定义最小路集矩阵为S，对每个最小路定义一个n维向量 Ei（x1, x2,…xn），n为边的条数。向量Ei的每个分量是一个二进制数字。xk取1时表示最小路中含有xk，当xk取0时表示不包含xk支路。

（2）计算

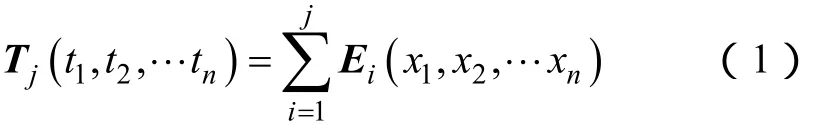
（3）定义互不相容的最小路集矩阵为Ldis，求互不相容的最小路Ljdis

①先令 j=1，L1dis=E1；

②再令 j=j+1；

1）比较Tj和Ej，如果Tj中某些非零元素位置（-11011）上Ej的元素为零，那么就按它们在Tj中的位置号码由大到小（或由小到大）记下它们的位置，令这些位置标号为 K1, K2,…,Kr。

2）把Ej对Kr分解为两个分量 Ej（Kr）和，它们分别用1和-1代替Ej向量第Kr位置上的“0”。然后检查Ej（Kr）和，如果 Ej（Kr）中有1的位置包含了任一Ei（i＜j）全部有 1的位置，那么Ej（Kr）就删去；若每个Ei（i＜j ）中有1(-1)的位置至少有一个与 Ej（Kr）中同位置的-1(1)相对应，说明Ei与 Ej(Kr)不相交，则 Ej（Kr）留下，它便是不交化了的子集。对于也作相似的处理。

3）如果Ej（Kr）不删去，也不留下，则继续分解，在Ljdis中数“1”对应元件完好，数“-1”对应元件故障，“0”表示不含此元件。

经过上述不交化过程之后得到的最小路集矩阵Ldis中的任意两条最小路之间都是互不相容的，因此，系统可靠工作的概率就可以表示为各条最小路成功运行概率之和。可按照如下公式计算节点可靠工作的概率Rs：

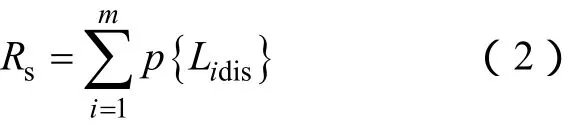
式中，Lidis为第i条不相容的最小路；m为求得的不交化最小路的条数。

现以图1为例说明上述求解过程。根据图2的搜索树，可以得到最小路集矩阵为

最后得到不交化的最小路矩阵为

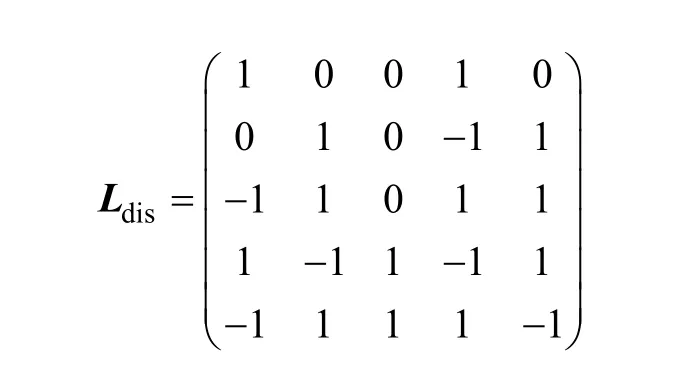
求出不相交最小路集后，系统可靠工作概率Rs即不相交最小路之和的概率，故

3 计及节点恢复成功率的分区策略

3.1 电网中节点恢复成功率的求解

应用最小路集理论对节点恢复成功率进行分析时，首先要将电力网络简化为一张拓扑图。简化原则如下：

（1）电网拓扑模型中的所有发电厂节点、变电站节点和负荷节点均抽象为网络中无差别的节点，且不考虑接地点。

（2）所有高压输电线路和变压器支路均抽象为网络中带权值的边。

（3）在恢复过程中，为了减少对地电容的影响，一般只投双回线路中的一回，因此在网络简化时可以合并双回线，且忽略并联电容支路。

按照上述简化原则，一个复杂的电力网络就可以由一张无向图表示，记为 G={V, E}，其中 V为节点，E为边。

本文假设所有节点的恢复成功率仅仅是由起始节点和目标节点之间的线路结构和线路恢复成功率决定的，不考虑节点本身存在的风险。由于电力网络是一个规模较大、结构较复杂的网络，在利用最小路集求解节点恢复成功率时，如果简单按照第 2节中论述的搜索树的方法进行求解，是非常困难的。本文以上述方法为基础，对实际的算法进行了两点改进：

首先，本文采用有界深度优先搜索策略来搜寻合适的最小路集，即为搜索设定了一个深度界限d，从起始节点出发，搜索了d步之后，如果仍然没有到达目标节点，则放弃搜索，选择另一条路进行搜索。深度界限d是由传统Dijkstra算法求得的两点之间的最短路径的长度确定的。

其次，本文采用动态搜索过程，即每恢复一个节点，都应该更新已带电节点数组和已恢复支路矩阵，下一次搜索最小路集时，从所有带电节点依次搜索到达目标节点的最小路。对于某一目标节点b，如果在之前的恢复节点a的路径中已经得到恢复，则其恢复成功率设定为等于恢复节点 a成功的概率。

3.2 节点分区的判定函数

系统分区并行恢复的目的是在尽可能短的时间内恢复尽可能多的机组出力，并快速建立起一个稳定的骨架网络。考虑到这两方面的因素，结合本文提出的节点恢复成功率的概念，建立如下的分区判定函数，以此来确定目标节点所属分区

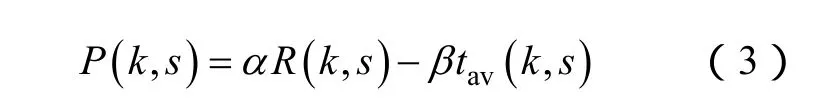
式中，k为节点编号，s为分区标号，R（k, s）为k节点由s分区恢复时恢复成功率；tav(k, s)为k节点由s分区恢复时平均路径恢复时间，即最小路集中所有路径恢复时间的平均值，本文中，对于一组恢复路径的时间，tav(k, s)的值均除以其最大值，进行了归一化处理；α、β为权系数，权系数值的确定原则是尽量使得时间指标和可靠性指标能够互相均衡，避免出现某个指标过大而造成另一个指标完全淹没的情况，且满足α+β=1。可以看到，分区判定函数从网络恢复结构的可靠性以及恢复的快速性两个方面衡量节点k由s分区中带电节点恢复的优劣性。与以往分区过程中仅仅依靠时间指标或者输电线路恢复代价指标等判据相比，此判定函数增加了网络可靠性的考虑，更加切合实际情况。

3.3 节点最优恢复路径的确定

根据同一待恢复节点由不同黑启动分区恢复时分区判定函数值的不同，可以快速确定其所属的最佳分区，但并不能确定恢复该节点具体的恢复路径。考虑到待恢复机组节点大部分为火电机组，且发电机组从点火到带负荷所用时间以及机组的爬坡率都和机组恢复供电的时间有很大关系。机组越快得到启动功率，就能够越快地恢复带负荷能力，因此，选择一条恢复用时最短的路径，对于提高机组的恢复出力以及加快系统的恢复进程，都具有重要意义。本文对于确定了所属分区的待恢复节点，直接从之前求得的该节点到达指定分区的最小路集中选择恢复时间最短的那条路径作为其恢复路径。

4 黑启动分区优化的实现

4.1 分区优化目标函数的建立

根据黑启动分区并行恢复优化策略的原则，提取以下指标来衡量分区结果的优劣。

首先，提取衡量分区后子系统网架重构效率的指标 f，定义如下：

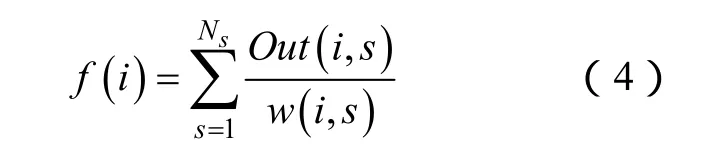
式中，i为方案编号；s为分区标号；Ns为分区数目；Out（i, s）为在恢复时限内；s分区内的所有发电机出力总和，不同发电机节点出力大小的确定方法同文献[11]；w（i, s ）为s分区内骨架网络输电线路代价之和，网络中各输电线路恢复代价权值设定同文献[6]。f（i）的值越大，表明分区内子系统骨架网络重构效果越好。

其次，提取衡量各个分区恢复时间差别大小的指标 Dt（i），它代表方案i中各个分区的恢复用时的分散度，Dt（i）定义如下：

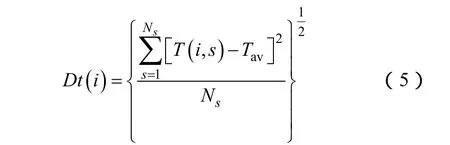
式中，T（i, s）表示方案i中，第s分区建立骨架网络的恢复用时；Tav为 Ns个分区建立骨架网络恢复用时的平均值，其计算公式为

最后，提取方案总恢复用时指标 Tmax（i），定义如下：

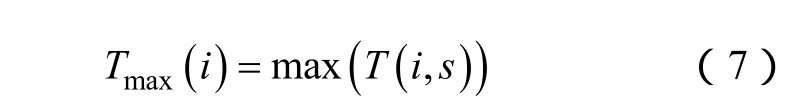
根据上述指标，建立如下分区优化目标函数：

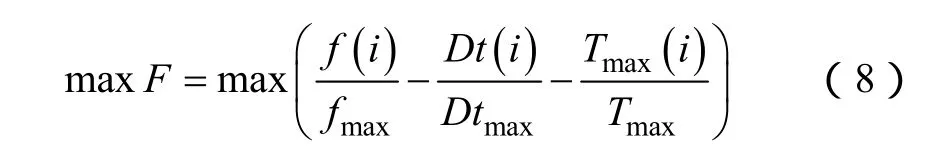
上述目标函数中，各个指标均除以其最大值进行归一化。目标函数从各个子系统网架重构效率、各子系统恢复用时差别以及整个网络重构时间的长短三个方面对分区结果进行评价。

4.2 约束条件

对于所有分区，均有以下约束：

（1）时间约束

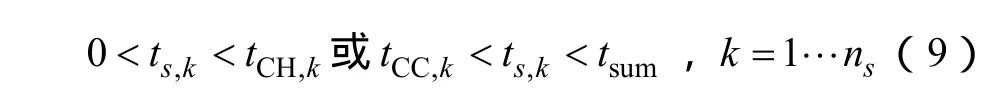
式（9）表示对于汽包式锅炉的发电机组通常具有最大临界时间限制，即在此时限内机组恢复供电，机组就可在极热态启动，直接带负荷。而对于具有直流式锅炉的发电机组，则有最小临界时间限制，停机后需要间隔一段时间才能重启。k为机组编号，ns为s分区内的机组数目。

（2）潮流约束

式中，x为系统状态变量；u为系统控制变量；p为系统扰动变量；Uk为节点电压；PGk为发电机组有功出力；QGk为发电机组无功出力；Pk，l为支路 k-l上流过的有功功率。

式（10）表示基本潮流方程，式（11）和式（12）表示机组有功出力和无功出力上、下限，式（13）表示节点电压上、下限，式（14）表示线路传输功率极限。

4.3 算法设计

本文采用交叉粒子群优化算法实现分区优化问题的求解。粒子群优化算法是由 Kennedy博士和Eberhart博士提出的一种全新的智能优化算法[12]。该算法初始化为一群随机粒子，每个粒子有它自己的位置和速度，还有一个被优化函数决定的适应值。在迭代过程中，各个粒子通过跟踪两个“极值”来更新自己。一个是粒子本身所找到的最优解，称为个体极值 pbest，另一个极值是整个种群目前找到的最优解，称为全局极值gbest。文献[13]将遗传算法中的交叉操作引入经典的粒子群算法，提出了交叉粒子群算法：让当前解与个体极值和全局极值分别作交叉操作，产生的解为新的位置。这里，每个粒子代表不同目标节点的恢复顺序。

在POS中，适应值习惯上按照从小到大的顺序排列，适应值越小，粒子越优。因此，本文中，适应值函数为目标函数的倒数。

式中，S是一个值很大的正数。算法求解过程的主要步骤如下：

（1）输入原始数据，进行数据初始化。包括：设定Ns个黑启动电源点，最大迭代次数Nmax，粒子数Np，并初始化Np个粒子，设定输电线路投运成功率p，令 i=1, j=1。

（2）取第i个粒子，令k=1。

（3）选择第k个待恢复节点，应用有界深度搜索算法寻找其到各个分区带电节点的最小路集，并根据线路恢复的成功率计算其由各分区恢复成功的概率 R（k, s），以及到达该分区恢复路径的平均时间tav（k, s）。

（4）计算第k个节点由s分区恢复的分区判定函数值P（k, s），并根据判定函数值的大小确定k节点所属分区，同时，从对应最小路集中筛选恢复时间最短的路径作为恢复该节点的具体路径。更新该分区带电节点数组。

（5）判断是否恢复完粒子i中的所有节点，如是，进行下一步，否则，k=k+1，返回（3）。

（6）计算并提取分区方案i的各项指标，如子系统重构效率指标f（i）、各分区恢复时间方差指标Dt（i）、整个网架重构时间 Tmax（i）等。

（7）判断是否已经计算完所有初始粒子，如是，进行下一步，否则，i=i+1，返回（2）。

（8）按照式（8）以及式（15）计算此组粒子的适应值函数值，选择出局部极值pbest，记录局部极值对应的粒子gxbest，并与全局极值gbest进行比较。如果 pbest＞gbest，更新全局极值，gxbest=pxbest ，gbest=pbest。初始粒子J与全局极值进行交叉，得到新的一组粒子；如果pbest≤ gbest ，则判断有多少次迭代全局极值已经没有变化，如果迭代次数大于50，则跳出循环，重新选择一组初始粒子进行计算，否则初始粒子J直接与全局极值交叉，得到新的一组粒子。

（9）j=j+1，转至（2），直到j=Nmax，此时判断得到的最优解是否收敛，如果较前几次迭代目标函数值还有明显的变化趋势，则继续迭代，直到所得到的解收敛。最后，输出gbest和gxbest。

交叉粒子群算法虽为人工智能算法，但其也存在计算量大和耗时长等缺点。为了提高算法的效率，避免程序陷入局部最优解，本文在（8）加入一个判定指标，即每次迭代结束后，比较最优解的适应值函数较上一次的变化，如果多次迭代适应值函数值都没有变化，则程序判定为陷入局部最优，程序将自动跳出循环，选择一组新的初始粒子进行迭代，直到到达最大迭代次数。

5 算例分析

根据本文介绍的分区优化算法，应用Matlab编程软件，以IEEE118节点作为算例，进行验证。该系统包含118个母线节点，186条线路和54台发电机。本为选择黑启动电源点为[1 54 99]，设定其余51台发电机组中汽包式锅炉37台，直流式锅炉14台。并设定交叉粒子群算法最大迭代次数Nmax=200，初始粒子数目 Np=10。网架中每条输电线路恢复成功率的大小，对节点恢复成功率的计算有重要的影响，由于缺乏实际统计数据，对于输电线路恢复的成功率本文采用假设的数值，但这并不影响对本文分区优化方法的有效性验证。本文算例中设定p=0.9。

首先，由于分区判定函数式（3）中的权值α、β设定的不同，对分区的结果有着直接的影响，考虑到本文中的节点恢复成功率和归一化后的路径平均恢复时间指标均为小于 1的值，本文优先选择α=0.5，β=0.5作为基准，调用所编写的程序得到最优分区方案。分区骨架网络如图3所示，分区结果的总体情况见表1。

图3 α=0.5，β=0.5时的最优分区网架图Fig.3 The optimal skeleton network when α=0.5，β=0.5

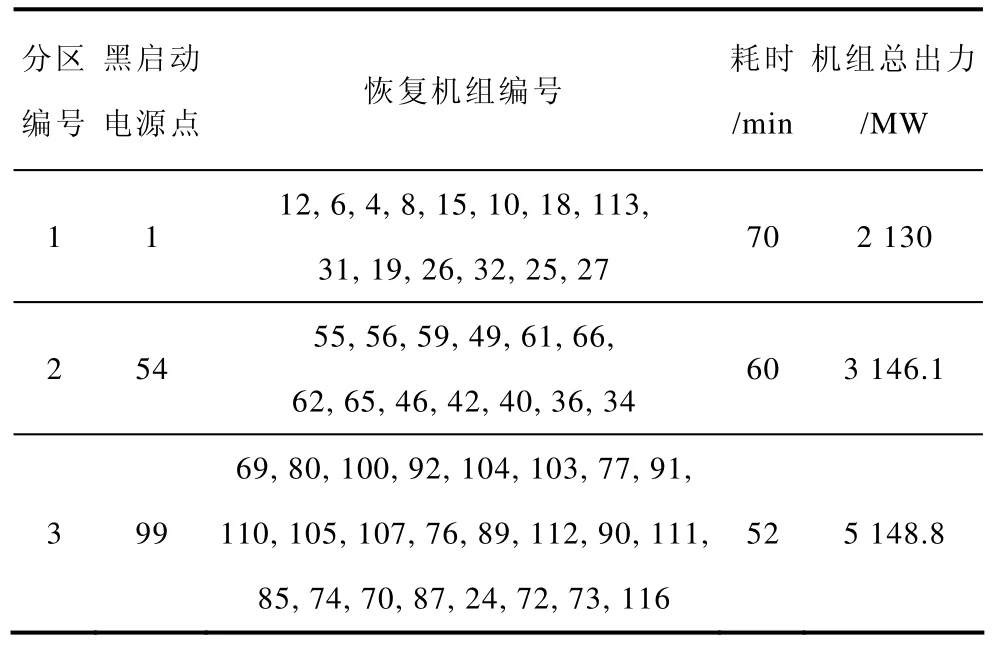
表1 α=0.5, β=0.5时的分区总体情况Tab.1 The optimal system partitioning scheme under the condition that α=0.5, β=0.5

由上述分区结果可以看到，第3分区机组数目较多，发电量偏大，各个分区的时间差别较大，所以，根据这种情况，应加大时间指标所占的比重，使得各分区之间恢复的时间差更小，各分区规模更为一致。因此，设定α=0.4，β=0.6重新进行最优分区策略的筛选。结果如图4和表2所示。

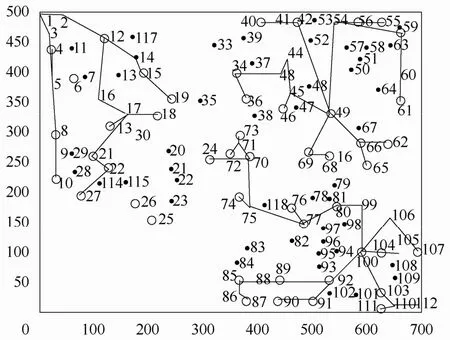
图4 α=0.4, β=0.6时的最优分区网架图Fig.4 The optimal skeleton network when α=0.4，β=0.6

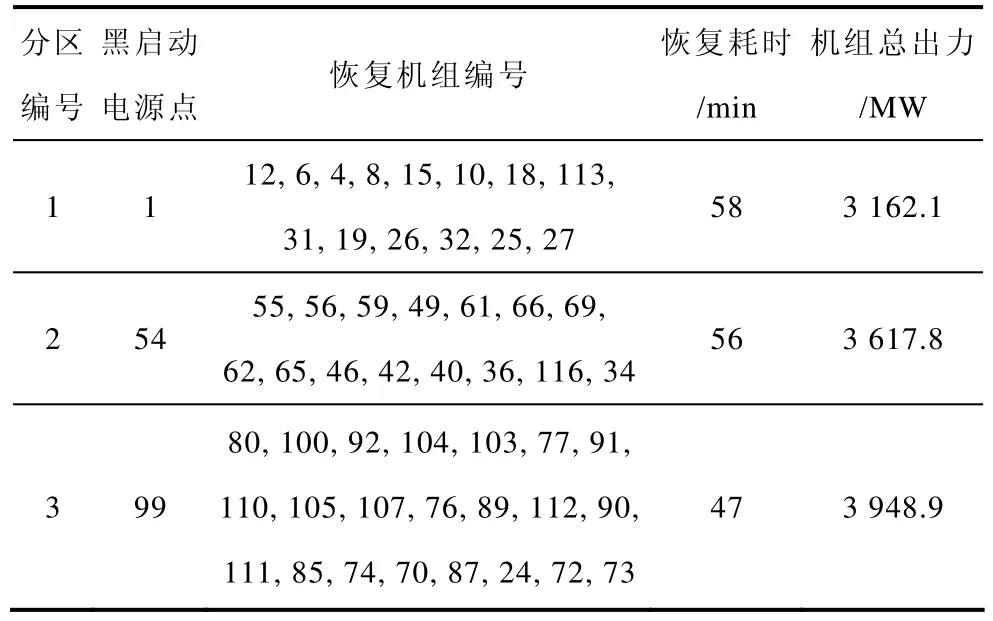
表2 α=0.4，β=0.6时的总体分区情况Tab.2 The optimal partitioning scheme under the condition that α=0.4，β=0.6

由上述两组结果对比可以发现，分区判定函数的权值系数调整之后得到的的分区结果，各个分区规模更加一致，各个子系统恢复用时相差变小，各分区发电量也趋于平衡，是一种较优方案。表3列出了分区1的详细恢复情况，包括节点的恢复顺序、各发电机节点的恢复路径以及每台机组得到启动功率的具体时刻。另外两个分区的详细恢复情况见表4和表5。

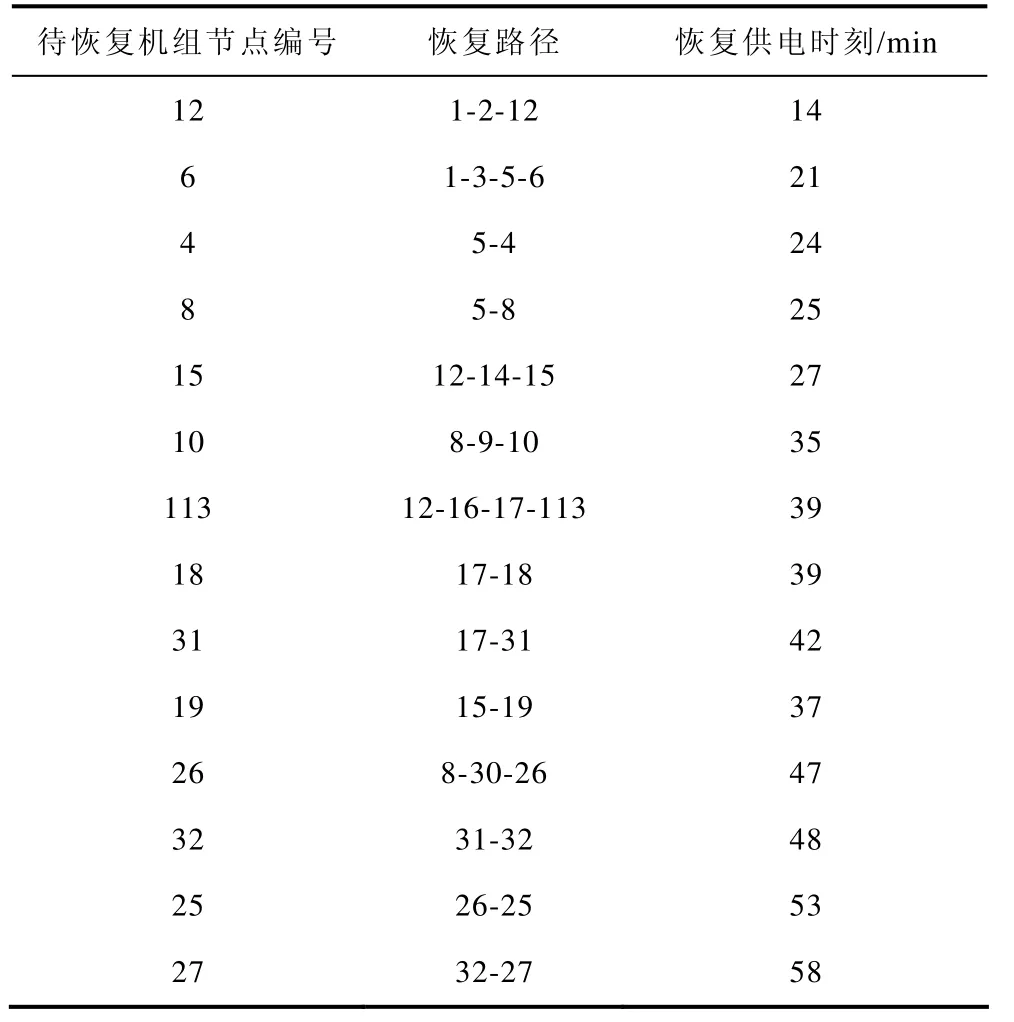
表3 分区1内机组的恢复情况Tab.3 Restoration status of units in zone 1

表4 分区2内机组的恢复情况Tab.4 Restoration status of units in zone 2

表5 分区3内机组的恢复情况Tab.5 Restoration status of units in zone 3

由上述分区结果可以看到，根据所选择的黑启动电源点的位置和分布，应用本文提出的方法，118节点系统被有效分割成以各黑启动电源点为核心的三个分区，且三个分区构建骨架网所用时间分别为58min、56min和47min，基本相当，骨架网络结构以及各分区内机组的出力情况也基本一致，实现了本课题最初关于分区并行恢复的目标。

为了进一步说明本文所编写的程序在对网络分区方案初始解进行优化的能力，本文将迭代过程中目标函数值的变化趋势进行了输出，如图5所示。可以清晰看到，迭代过程是向着目标函数值不断变大的方向进行的，即目标函数朝最优方向发展。与初始解以及迭代过程中随机设定的一组解相比，本文在迭代280次之后得到的最优分区方案，在恢复时间和分区规模方面有了很大程度的改进。

由于此时还处于黑启动恢复的初期，仅仅是以最大程度恢复发电机组作为目标进行的分区子系统骨架网络的构建，因此，子系统内潮流校验时，各被恢复机组的出力取其最大值的30%，并保证各机组的出力在调节过程中，不低于该初值。

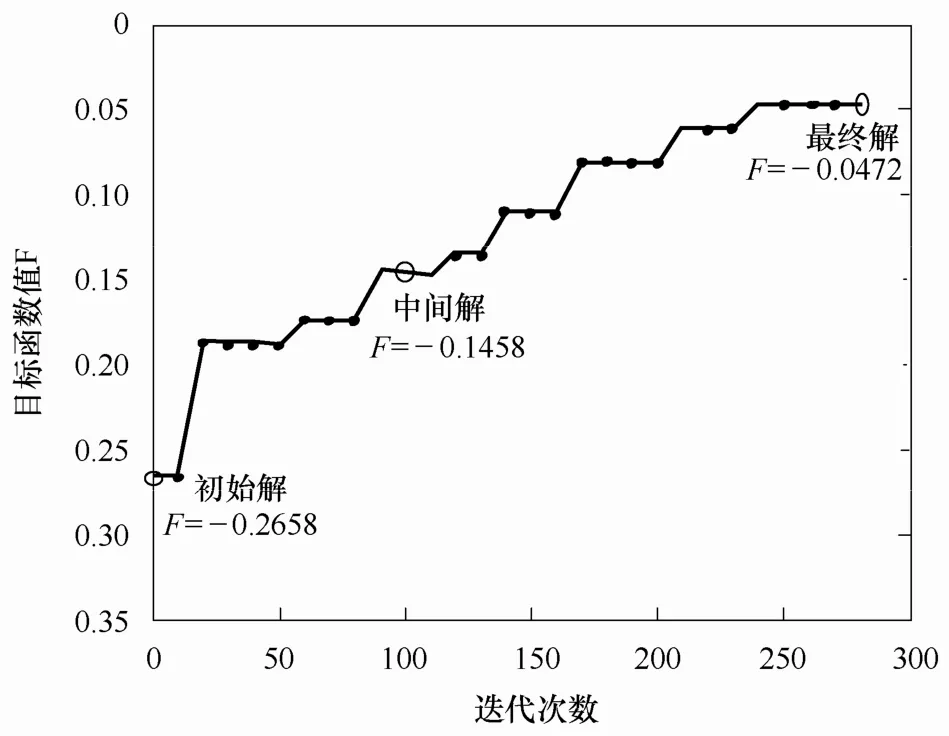
图5 最优解的目标函数值变化曲线Fig.5 The curve of objective function value of optimal solution

6 结论

本文提出了大停电事故后初期电网分区恢复方案的优化方法。较以往分区方法相比，本文充分考虑了复杂网络输电线路投运的不确定性以及网络结构变化的灵活性，并将其量化，将基于最小路集求解节点恢复成功率的方法应用到电网节点恢复过程中，建立了求解节点恢复成功率的数学模型，同时结合系统恢复的快速性要求，建立了新的节点分区判据，实现对待恢复节点的有效分区。本文提取了评价子系统重构效率的指标、各分区恢复时间方差指标以及网络重构时间指标等，建立了分区方案优化目标函数，应用交叉粒子群优化算法对分区结果进行综合评价和优选。IEEE118系统算例的分区优化结果证明了本文所提方法的可行性和有效性。

[1]刘映尚, 吴文传, 冯永青, 等.基于有序二元决策图的黑启动分区搜索策略[J].中国电机工程学报,2008, 28(10): 26-31.Liu Yingshang, Wu Wenchuan, Feng Yongqing, et al.Black-start zone partitioning based on ordered binary decision diagram method [J].Proceedings of the CSEE, 2008, 28(10): 26-31.

[2]林振智, 文福拴, 周浩.基于复杂网络社团结构的恢复子系统划分算法[J].电力系统自动化, 2009,33(12): 12-16, 42.Lin Zhenzhi, Wen Fushuan, Zhou Hao.A new algorithm for restoration subsystem division based on community structure of complex network theory [J].Automation of Electric Power Systems, 2009, 33(12):12-16, 42.

[3]吴烨, 房鑫炎, 张焰, 等.基于禁忌搜索算法的黑启动子系统划分[J].电力系统保护与控制, 2010,38(10): 6-11.Wu Ye, Fang Xinyan, Zhang Yan, et al.Tabu searching algorithm based black-start zone partitioning [J].Power System Protection and Control,2010, 38(10): 6-11.

[4]周敏, 刘艳.计及火电机组启动过程的网架并行恢复策略[J].电力系统自动化, 2011, 35(10): 30-34, 93.Zhou Min, Liu Yan.A parallel restoration strategy for power network considering the start-up process of thermal units [J].Automation of Electric Power Systems, 2011, 35(10): 30-34, 93.

[5]Orero S O， Irving M R.A genetic algorithm for network partitioning in power system state estimation[J].IEEE Transactions on Power Systems, 1996, 45(5): 162-165.

[6]顾雪平, 韩忠晖, 梁海平.电力系统大停电后系统分区恢复的优化算法[J].中国电机工程学报, 2009,29(10): 41-46.Gu Xueping, Han Zhonghui, Liang Haiping.Optimization of parallel restoration through power system partitioning after blackout [J].Proceedings of the CSEE, 2009, 29(10): 41-46.

[7]赵冬雯, 梁海平, 顾雪平.基于遗传算法的黑启动分区恢复方案的选定[C].中国高等学校电力系统及其自动化专业第二十四届学术年会论文集, 北京:2008.

[8]韩忠晖, 顾雪平, 刘艳.考虑机组启动时限的大停电后初期恢复路径优化[J].中国电机工程学报,2009, 29(4): 21-26.Han Zhonghui, Gu Xueping, Liu Yan.Optimization of restoration paths considering unit start-up time reuirements at early stage of power system restoration[J].Proceeding of the CSEE, 2009, 29(4):21-26.

[9]Wang Chong, Vittal Vijay, Kolluri Venkat Sharma, et al.PTDF-based automatic restoration path selection[J].IEEE Transactions on Power Systems,2010, 25(3):1-10.

[10]郭永基.可靠性工程原理[M].北京: 清华大学出版社, 2002.

[11]刘强, 石立宝, 周明, 等.电力系统恢复控制的机组优化启动策略[J].电力自化设备, 2009, 29(4): 1-5.Liu Qiang, Shi Libao, Zhou Ming, et al.Optimal strategy for units start-up during power system restoration[J].Electric Power Automation Equipment,2009, 24(3): 164-170.

[12]Kennedy J, Eberhart R.Particle swarm optimization[C].Proceedings of IEEE International Conference on Neural Networks, Perth, 1995.

[13]高尚, 杨靖宇.群智能算法及其应用[M].北京: 中国水利水电出版社, 2006.