基于相电压重构的三电平PWM整流器的研究

何至源，倪榛潞，魏星，李媛

（江西宜春供电公司，江西 宜春 336000）

1 引言

目前国内应用的PWM整流器大多以两电平为主，相比两电平而言，三电平PWM整流器在同等情况下不仅降低了对功率器件的要求，而且输出电压或电流的谐波也大为减少，同时在较低的开关频率上也能保证交流侧输入电流拥有一定的正弦度，可以说三电平是电力电子设备发展的一个重要趋势。

在分析PWM整流器的数学模型进而对其进行控制时，采用不同的定向矢量直接会影响到系统的控制性能，通常情况下采用的是电网电压定向，这种定向方法的不足之处在于：首先需加装交流电压传感器，在增加硬件成本的同时也增加系统的复杂度；其次当电网电压波形较差时（例如矿井提升机启动过程）电网电压定向会出现偏差，从而影响电流的解耦，进而影响整流器的整体控制性能［1］。

本文以三电平PWM整流器为研究对象，借鉴电机控制中磁链定向的思想，利用基于虚拟磁链定向方法来对电流进行解耦。在此方法中无需采用电网电压传感器，而是在简化三电平SVPWM算法基础上以一个周期中各矢量作用时间的占空比模型来重构每相电压，然后通过积分等步骤估算虚拟磁链以获取定向角度，由此实现对三电平PWM整流器的精确控制。最后通过实验验证该方案的可行性。

2 虚拟电网磁链的引入

三电平PWM整流器主电路简图如图1a所示，其中ua，ub，uc分别为三相电网电压，L，R是进线电抗器的电感与电阻，Udc为直流母线电压。图1b是一台由三电平逆变器供电的三相交流电机，其中ea，eb，ec分别为电机三相定子绕组的感应电势，Lσ和R分别是定子绕组的漏感与电阻。对比两图可以发现二者其实是相对应的，例如u与e，Lσ与L等。在交流电机的矢量控制中，一般采用磁链定向。由此得到在PWM整流器中，也可将电网电压看成一个虚拟磁链的微分量，并以这个虚拟磁链作为定向矢量，从而达到省去电网电压传感器的目的。

图1 三电平整流器、逆变器简图Fig.1 The simplified circuits of three－level PWM rectifier and inverter

3 三电平相电压重构算法

由文献［2］可知两电平相电压重构方程：

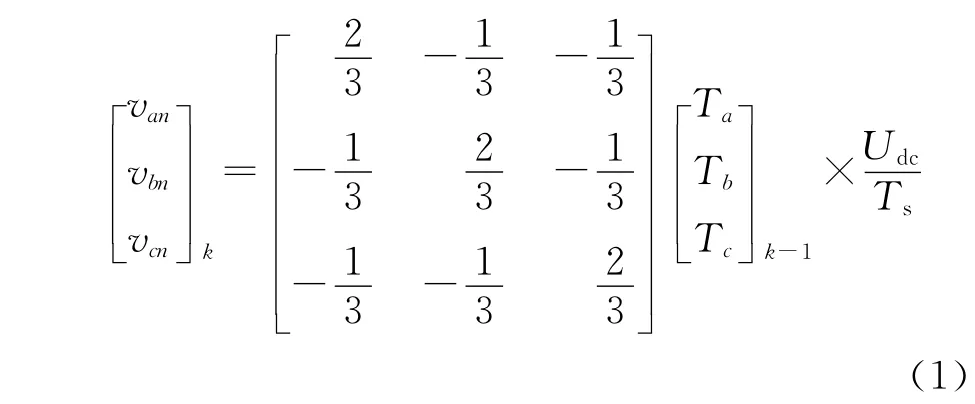
式中：vxn为整流器交流侧输入相电压；Udc为直流母线电压；Ts为周期时间；Ta，Tb，Tc为各相分别作用的时间。

相比于两电平，三电平显然要复杂的多，传统的三电平SVPWM控制算法思路清晰容易理解，但是矢量作用次序的选取、作用时间的计算过于复杂，不易为DSP实时处理。文献［3］中提出一种简化三电平SVPWM算法，此种方法将三电平空间矢量图分为6个相互重叠的扇区，利用给定空间电压矢量的平移，把三电平转化成两电平进行处理，大大减少了各矢量作用时间的计算量，同时通过调整正负小矢量的作用时间可以有效保证中点电位的恒定。基于此，我们在三电平简化SVPWM算法的基础上研究三电平相电压重构算法。

设在一个周期Ts内，Ta1，Tb1，Tc1分别为A相、B相、C相的作用时间，则有：

对于在三电平简化SVPWM算法下输出相电压的重构，同样可以利用坐标平移，把需要重构的电压矢量分别定位在以原点为中心的小六边形内进行。以给定电压空间矢量Vref在第2扇区为例，如图2所示。

图2 相电压重构中补偿电压示意图Fig.2 Voltage reconfiguration compensation voltage schematic

图2是Vref位于第2扇区时各相电压补偿值的示意图，同样可以得到参考电压位于其他扇区时各相的补偿量。不同S值下补偿电压如表1所示。

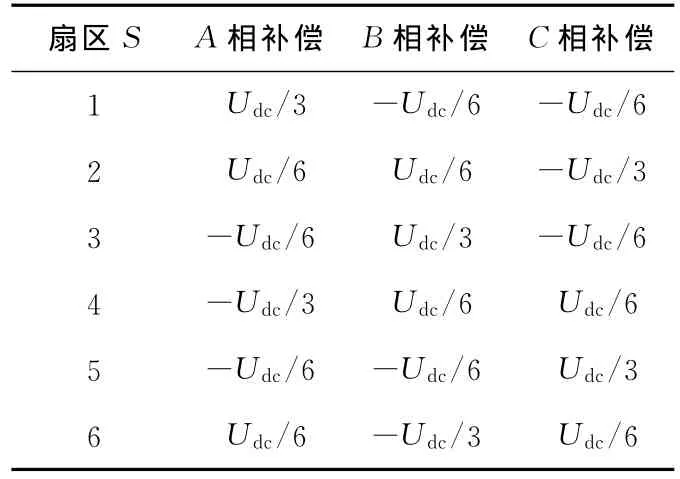
表1 不同S值下补偿电压Tab.1 Compensation voltage with different S Values

所以三电平PWM整流器相电压重构的公式如下：

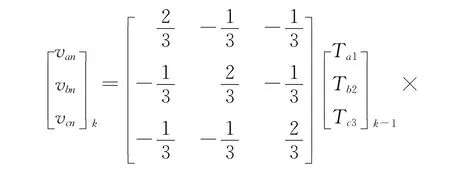
4 基于虚拟磁链定向的三电平PWM整流器数学模型

图3为三电平PWM整流器拓扑结构图。

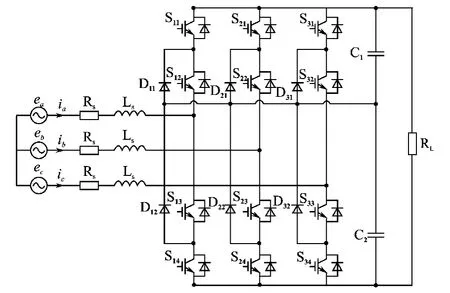
图3 三电平PWM整流器拓扑结构图Fig.3 The topology structure of three－level PWM rectifier

根据文献［4］可得三电平VSR在αβ坐标系下的数学模型：

忽略交流侧等效电阻Rs可得：

对上两式的两边同时积分，可得：

定义虚拟电网磁链为

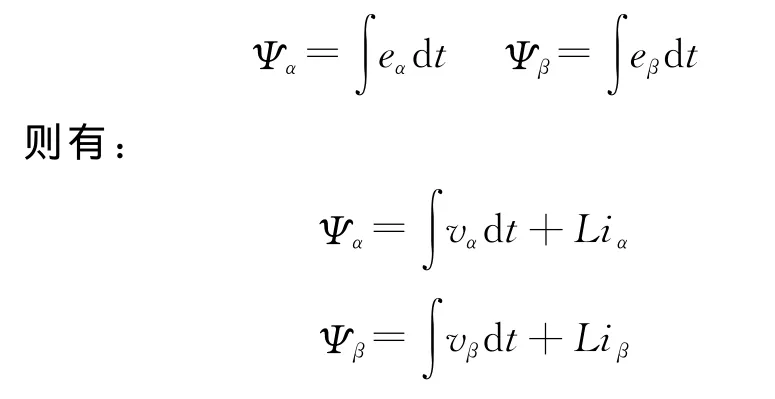
所以可求得虚拟磁链角度为

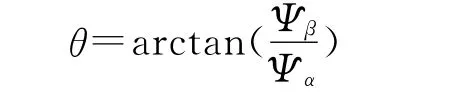
由上可知在计算虚拟磁链的过程中存在着积分环节，这就需要在积分运算前确立积分初值，否则无法得到准确的虚拟磁链。为了克服这一问题，采用3个一阶低通环节级联以代替纯积分，如图4所示。

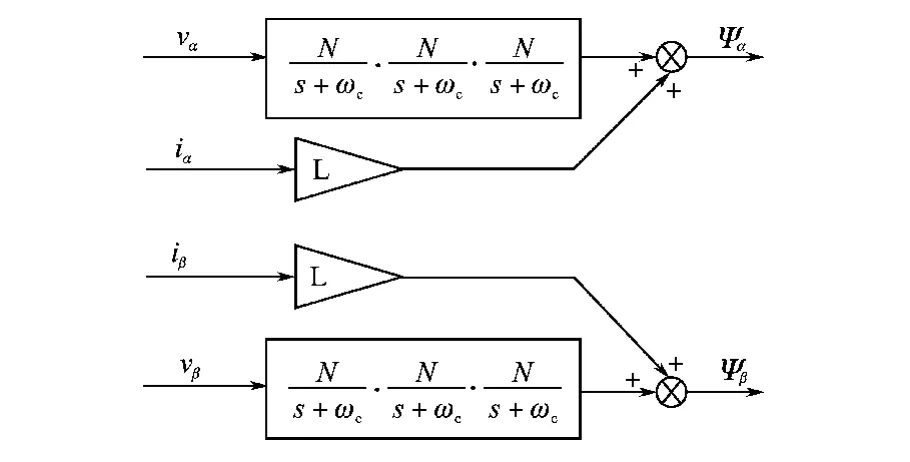
图4 虚拟磁链观测器Fig.4 Virtual flux observer

为使观测值与实际值幅相无差，令

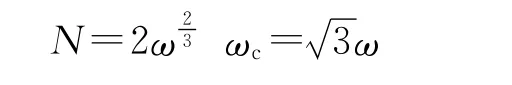
设dq旋转坐标系初始角度与a相的初始角度相同，则可求出三电平整流器在虚拟磁链定向下的数学方程：

5 三电平PWM整流器的电流解耦与控制方法

为了让d，q轴电流更好地解耦，电压外环与电流内环均采用PI控制器，参照式（3）引入前馈解耦［5］可得：

系统控制结构框图如图5所示。

图5 三电平PWM整流器矢量虚拟磁链定向控制原理框图Fig.5 The principle block diagram of the three－level PWM rectifier based on virtual flux

6 实验研究

为了验证上述方法在实际中的可行性，以德州仪器的TMS320F2812为主控芯片，搭建一套20 kW的双三电平调速平台，以双馈电机为负载，对基于虚拟磁链定向的三电平整流器系统进行试验研究。电网线电压＝380V，直流母线电压给定650V，进线电抗L＝0.4mH，直流母线电容Cup＝Cdown＝4700pF，功率器件开关频率约为2kHz。图6为三电平整流器的实验波形。

图6中各量分别为由标幺处理的相电压uα、相电流iα、上、下母线电压Uup与Udown，其中电压基值为500V，电流基值为50A。图6a为三电平PWM整流器负载突变时的波形；图6b为三电平PWM整流器由整流状态转变为有源逆变状态时的波形，此时双馈电机正通过整流器向电网馈送能量。

由图6可知，系统工作性能良好，网侧相电压电流基本同相位，功率因数近似为1，直流母线电压稳定，纹波较少，在负载突变与工作模式转变时依然能快速恢复，且恢复过程中相电流始终保持正弦。

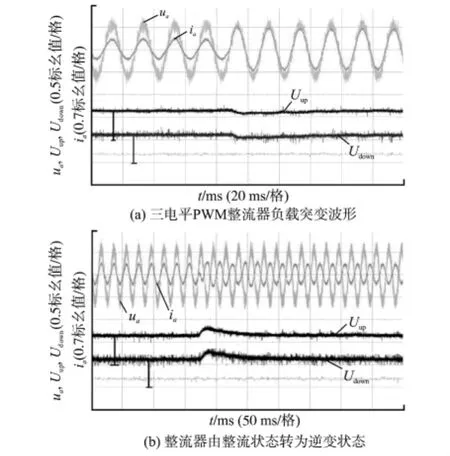
图6 三电平整流器的实验波形Fig.6 Experiment waveforms of the three－level PWM rectifier

7 结论

本文在三电平简化SVPWM算法基础上提出一种三电平相电压重构算法，由此建立了基于虚拟磁链定向的三电平整流器的数学模型，并使用PI控制器对其控制。实验结果表明，在省去电网电压传感器的情况下，系统仍实现了近似单位功率因数运行，并且具有直流母线电压稳定性好、输入电流正弦度高、系统动静态性能优良等特点，这些都证明了基于虚拟磁链定向下三电平PWM整流器拥有良好的静、动态性能，这对于其在电网电压发生畸变时的精确控制有着极为重要的意义，具有良好的应用前景。

［1］赵仁德，贺益康.无电网电压传感器三相PWM整流器虚拟电网磁链定向矢量控制研究［J］.中国电机工程学报，2005，25（10）：56－61.

［2］韩利，温旭辉，郭希铮.电压源逆变器输出电压重构技术研究［J］.电力电子技术，2007，41（11）：94－96.

［3］Seo J H，Chang Ho Choi，Dong Seok Hyun.A New Simplified Space－vector PWM Method for Three－level Inverters［J］.IEEE Trans.on Power Electron，2001，4（7）：545－547.

［4］叶宗彬.大功率提升机三电平双馈调速关键技术研究［D］.徐州：中国矿业大学，2011.

［5］张崇巍，张兴.PWM整流器及其控制［M］.北京：机械工业出版社，2003.