新的具有最优平均汉明相关性的跳频序列族
2012-08-14柯品惠章海辉张胜元
柯品惠,章海辉,张胜元
(福建师范大学 网络安全与密码技术重点实验室,福建 福州 350007)
1 引言
跳频码分多址(FH-CDMA)扩频系统具有抗干扰、抗截获的能力,并能做到频谱资源共享,所以在蓝牙、超宽频、雷达等当中都得到了广泛的应用[1,2]。
在跳频多址扩频系统中,当接收器解调来自发送器传送的信号时,会受不明信号的干扰。为了防止相互干扰,采用的跳频序列的汉明互相关值和非平凡的汉明自相关值应尽可能小。
迄今已有的关于跳频序列的汉明相关最优性的判定方式有如下2种。
一种是最大的汉明相关值[3,4],另外一种是平均汉明相关值[5]。近年来,跳频序列的设计已成为人们关注的热点,其中大部分都是针对最大的汉明相关值构造出最优的跳频序列族[6~10]。而平均汉明相关值代表的是跳频多址扩频系统平均误差,因此,设计出具有达到平均汉明相关界的跳频序列族也是非常有意义的。基于模p的高次剩余及Whiteman广义分圆类,文献[11]和文献[12]分别构造了达到平均汉明相关界的跳频序列族。然而,较之达到最大汉明相关界的跳频序列,公开发表的达到平均汉明相关界的跳频序列族的结果比较少。
Ding-Helleseth广义分圆类及Whiteman广义分圆类是2种重要的分圆类。人们对上述2种分圆类进行了各种推广,并由此构造了一系列性质良好的序列。最近,Meidl在文献[13]中给出了Ding-Helleseth广义分圆的推广,进而利用该推广的分圆类构造了多值序列,并分析了该序列的自相关值及错综复杂度等性质。本文首先给出Whiteman广义分圆类的一个推广,然后应用推广的广义分圆类构造一类新的跳频序列族,并计算了它们的平均汉明相关值。最后证明了新构造的跳频序列族关于平均汉明相关界是最优的。注意到,当d=2n时,此时推广的Whiteman广义分圆类等同于Whiteman广义分圆类,从而本文的结果推广了文献[12]的结论。
2 预备知识
设F={f0,f1,…,fv-1}为频率集,令U是F上的周期为L,序列条数为M的跳频序列族。U中的任意2条跳频序列X={x0, x1,…,xL-1}, Y={y0,y1,…,yL-1}的周期汉明相关函数定义为

这里
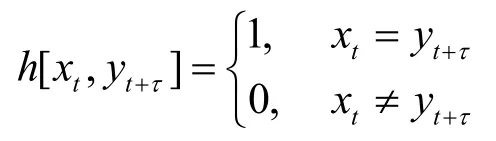
其中,下标是模L运算。若X=Y, HX,X(τ)称为X的汉明自相关函数,简记为HX(τ)。X的最大汉明自相关以及X与Y(X≠Y)的最大汉明互相关分别定义为

Lempel和Greenberger在1974年给出了H( X)的一个下界。
引理1[3]设U是F上周期为L的跳频序列,则
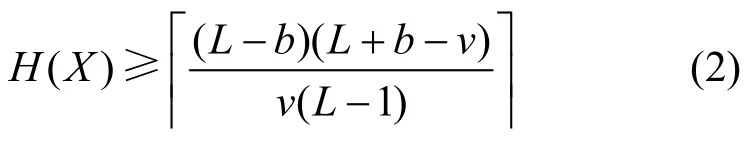
其中,|F|=v,b是L模v的非负整数,|x|表示为大于或等于x的最小整数。
对任意给出的一个跳频序列族U,最大的汉明自相关Ha( U)和最大的汉明互相关Hc( U)分别定义为

关于跳频序列族,Peng 和 Fan 在2004年给出了如下一个理论界。
引理2[4]设U是F上周期为L,序列条数为M的跳频序列族,|F|=v,I =,则

跳频序列族的另外2个重要参数平均汉明自相关函数和平均汉明互相关函数分别定义如下:
定义1[14]设U是F上周期为L,序列条数为M的跳频序列族,则分别称

为U的总汉明自相关和汉明互相关。同时分别称
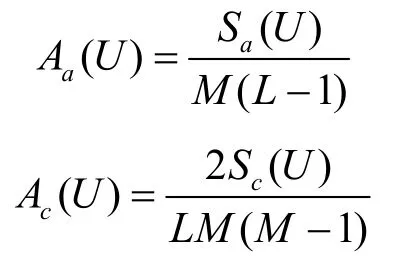
为U的平均汉明自相关和平均汉明互相关。为了简便,本文约定

最近,Peng等人给出了Aa和Ac的如下理论界。
引理3[15]设U是F上的周期为L,序列条数为M的跳频序列族,|F|=v,Aa和Ac分别为U的平均汉明自相关和平均汉明互相关,则
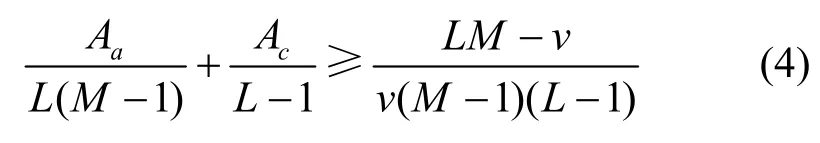
综上所述,关于跳频序列的最优性,有如下几种判定标准。
1) 对于单条跳频序列X∈U,如果参数v、L和H( X)使得式(2)等式成立,则称X是最优的。
2) 对于跳频序列族U,如果参数v、L、M、Hc和Hc使得式(3)中的任一等式成立,则称U关于最大汉明相关界是最优的。
3) 对于跳频序列族U,如果参数v、L、M、Aa和Ac使得式(4)等式成立,则称U关于平均汉明相关界是最优的。
由式(3)和式(4)易知,如果一个跳频序列集关于最大汉明相关界是最优的,那么它关于平均汉明相关界一定是最优的。但是,平均汉明相关界考虑的是一个序列集的全局性质,此时对一个跳频序列集,即使它关于最大汉明相关界不是最优的,但如果能达到平均汉明界亦是很好的性质[11]。更为重要的是,求平均汉明相关界的直接途径是给出所考虑的序列集的汉明相关值的分布,而一个跳频序列族的汉明相关分布和它对应的循环码的重量分布有密切联系[8],这是需要考虑这一问题的另一个主要原因。
3 广义分圆类及其推广
设p和q是不同的奇素数,gcd(p-1,q-1),=2n,n为整数,根据中国剩余定理,存在p和q的公共本原根,记为g。令x为满足下列同余方程组的整数解:
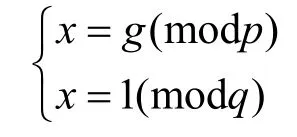
令e=(p-1)(q-1)/2n, L=pq,则ZL中所有可逆元的集合可表示为
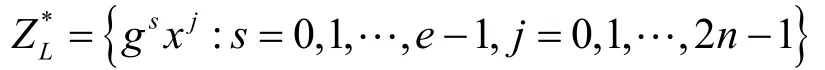
Whiteman广义分圆类定义如下[16]:
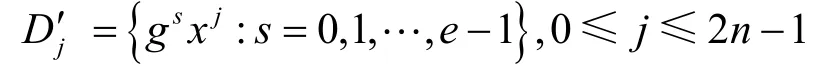
定义

引理4[16]符号同上,则
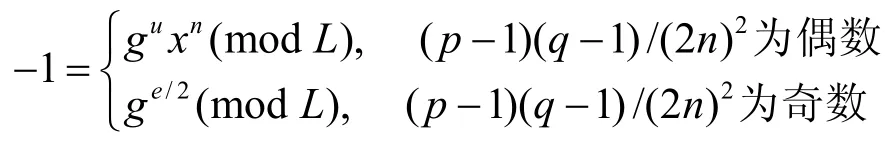
其中,u是某个给定的整数,且0≤u≤e-1。
现在给出Whiteman广义分圆类的一个推广。
设d|2n,且d为奇素数。定义


注意到,如上提出的是基于Whiteman广义分圆类的推广,它不同于Meidl等在文献[13]中提出的分圆类的推广,因为后者是基于Ding-Helleseth广义分圆类的推广。对于新推广的Whiteman广义分圆有如下性质。
性质1 设D0及(i, j)分别表示如上所定义的推广的Whiteman广义分圆类和分圆数,则:
1) -1∈D0;
2) (i, j)=(j, i);
3) (i, j)=(d-i, j-i)。
证明 1) 由d|2n,且d为奇素数,可知d| n,又由引理4可知,-1∈D0。
2)和3)易证。证毕。
性质2 对任一给定的i,0≤i≤d-1,有:
根据上文所提到的在互联网+视域下大数据对于管理会计所带来的挑战可知,当前要想全面发挥管理会计的积极作用,要求能够把握机遇,规避挑战。

证明 只证式(5)(式(6)可类似证明)。
1) 当ω∈Q时,结论显然成立。
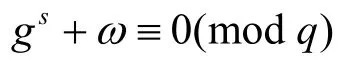
易知,有且只有一个s1∈Zq使得上述方程成立。因此,可设s=s1+k( q -1),由0≤s≤e-1可知,,所以对于z=gsxdt+i+ω∈Q∪R总共有
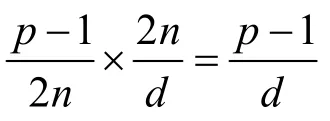
注1 显然有
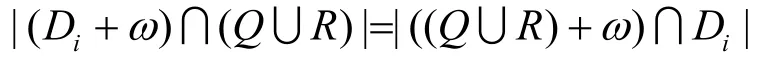
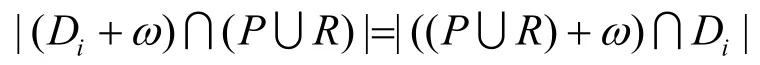
性质3
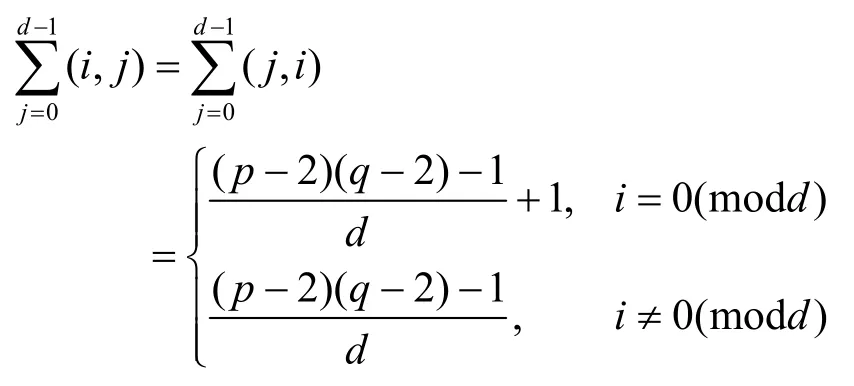
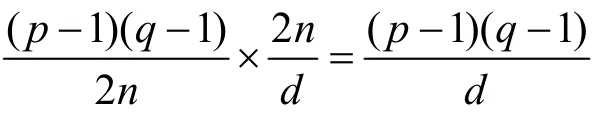
个元素。
1) 当i≡0(modd)时,Di+1中与L不互素的元素可分为如下3种情形。
① 元素能被L整除。 属于该情形的元素个数为1。
② 元素能被p整除而不能被L整除。属于该情形的元素个数为
③ 元素能被q整除而不能被L整除。属于该情形的元素个数为。因此,Di+1中共有
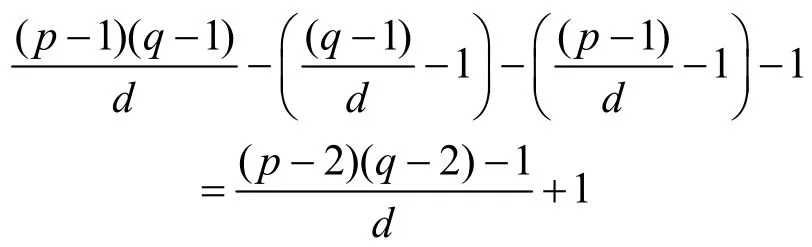
个元素与L互素,即

2) 当i≠0(modd)时,Di+1中与L不互素的元素可分为如下3种情形。
① 元素能被L整除。属于该情形的元素个数为0。
② 元素能被p整除而不能被L整除。属于该情形的元素个数为
③ 元素能被q整除而不能被L整除。属于该情形的元素个数为
因此,Di+1中共有
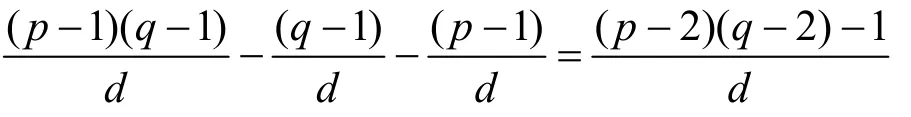
个元素与L互素,即

证毕。
性质4
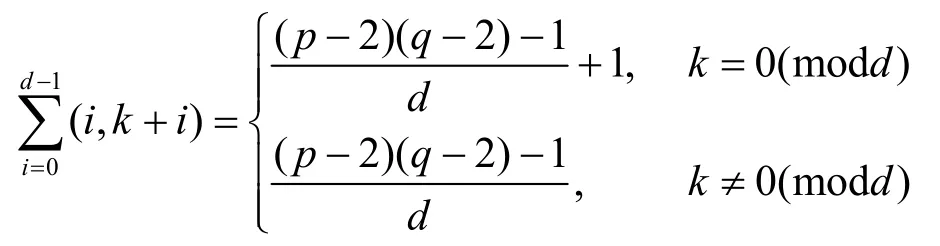
证明 由性质1中3)可知,
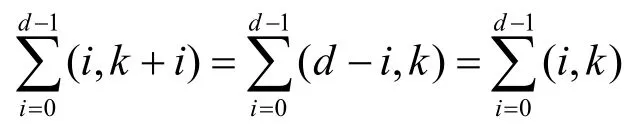
再由性质3,结论显然成立。证毕。

证明 只证式(7)(式(8)可类似证明)。
当ω∈P时,元素z∈(Di+ω)∩Di,此时
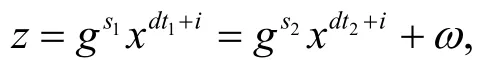
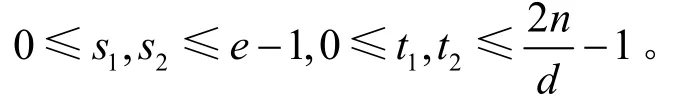
以下分2种情形讨论。
1) 当t1=t2时,由
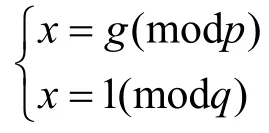
可知,gs1+dt1+i=gs2+dt2+i(modp),即gs1=gs2(modp)。不妨设s1=s2+m1( p-1),,则有

即gs2xdt2+i(gm1(p-1)-1)=ω(modpq )。又显然有gm1(p-1)-1=0(modp),因而,
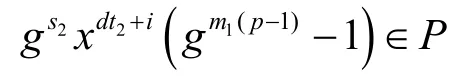
由gs2xdt2+i=gs2(modq), 设s2=s2′+h( q-1),,给定一个h,当s2遍历{h( q-1),h( q-1)+1,…,h( q-1)+q-2}时,
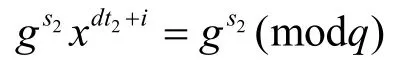
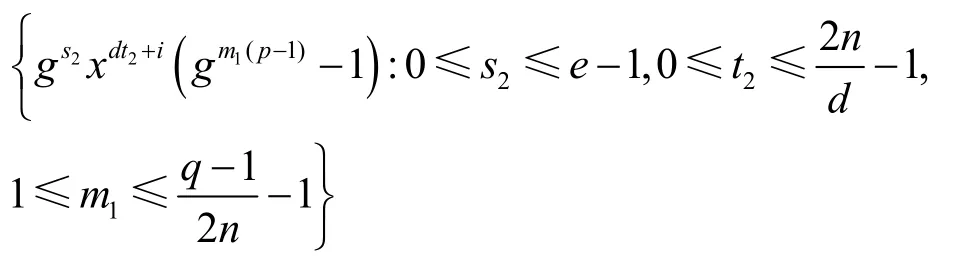
包含P中每一元素的次数为
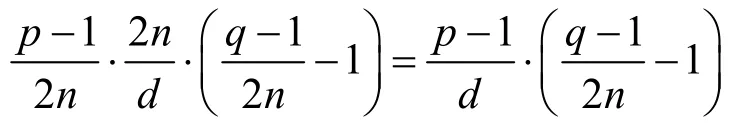
2) 当t1≠t2时,由

可知,gs1+dt1+i≡gs2+dt2+i(mod p ),即。假设

即s1=s2+d( t2-t1)+m2(p -1),则有:

由gs2xdt2+i=gs2(mod q),设

给定一个h′,当s2遍历{h′( q-1),h′( q -1)+1,…,h′( q-1)+q -2}时,gs2xdt2+i=gs2(mod q)对应中每一个元素恰好均出现一次,也就是对应P中的元素恰好出现一次,所以多重集
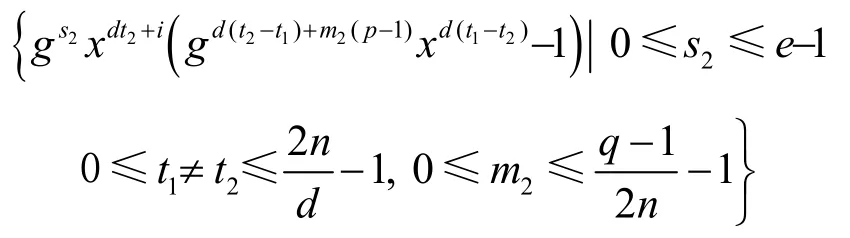
包含P中每一元素的次数为
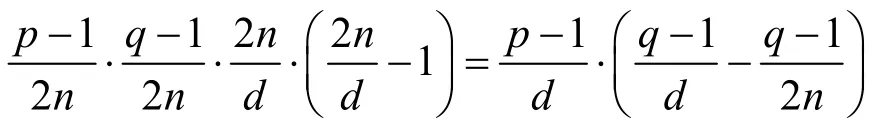
综合情形1)和情形2),方程gs1xdt1+i=gs2xdt2+i(modpq)的解个数为
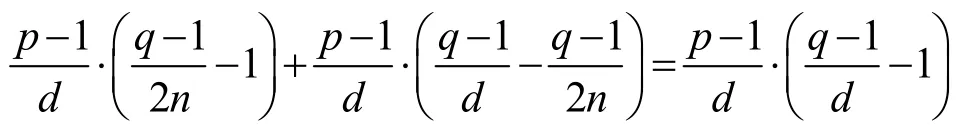
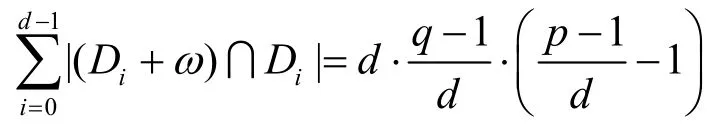
最后,当ω∈Dl,由定义ω-1Di=Di-l,有:
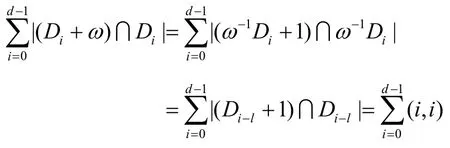
由性质4可得结论。 证毕。
性质6 对任一给定的i,0≤i≤d-1,有:
证明 1) 当ω∈Di时,ω-1Di=D0,由性质1可知,-1∈D0,从而
|(Di+ω)∩R|=|(ω-1Di+1)∩R|=|(D0+1)∩R |=1当ω∈/Di时,结论显然成立。
对2)及3),注意到
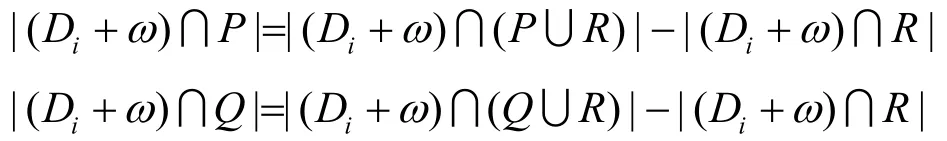
由性质2和性质6可得结论。证毕。
注2 显然有:
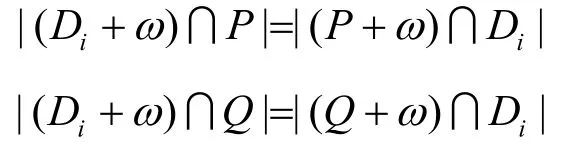
性质7[12]
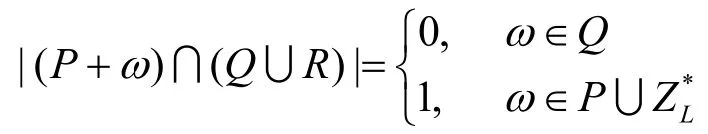
和

注3 1) 显然有:
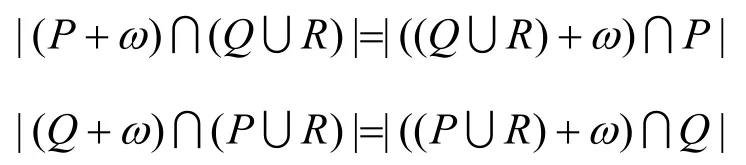
2) 类似地,容易验证
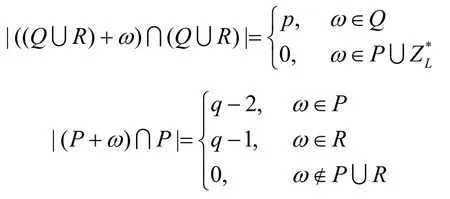
4 新的跳频序列族的构造
本节将构造一类新的跳频序列族,并利用上一节给出的推广的Whiteman广义分圆类的性质给出该跳频序列族的汉明相关值的分布,证明了该类跳频序列族关于平均汉明相关界是最优的。
令
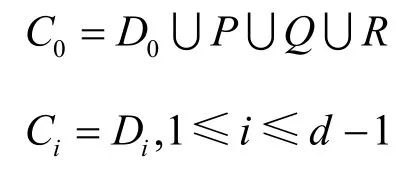
令X={x0, x1,…,xL-1}是在频率集F={0,l,…,d-1}上的周期为L的跳频序列,称
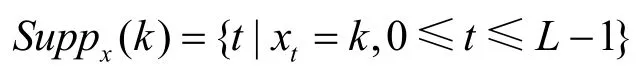
为k∈F在序列X上的支撑集。
定义2 设L=pq,Ci,0≤i≤d-1定义同上。定义跳频序列族U={X(i),i=0,1,…,d -1},其中,的支撑集为
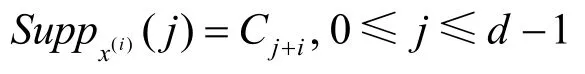
这里,j+i是模d运算。
定理1 令p和q是不同的奇素数,gcd(p-1,q-1)=2n,令d|2n,d为奇素数,则如上定义的跳频序列族U满足如下性质。
1) 序列族的大小为|U|=d,序列的周期为L=pq,频率集大小为|F|=d。
2) U中任意一条跳频序列(k)X的汉明相关函数值

3) U中任意2条不同的跳频序列X(k),X(l)的汉明互相关函数值
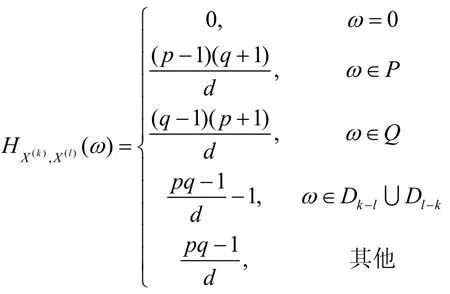
证明 1) 显然成立。
2) X(k)在ω移位的汉明自相关函数为

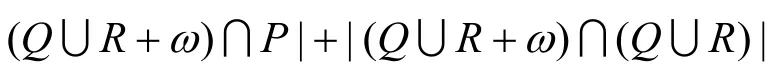
由性质2、4、6、7可得结论。
3) 任意不同的2条跳频序列X(k),X(l)∈U,0≤k≠l≤d-1,在ω移位的汉明互相关函数为
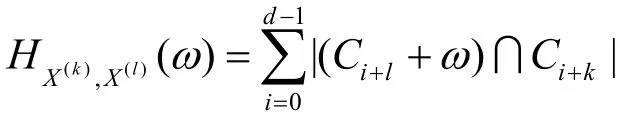
由d是奇素数可知,k-l≡/l-k(mod d ),令t=l-k
则由性质2、5、6可得结论。证毕。
定理2 跳频序列族U的平均汉明自相关和汉明互相关分别为

进一步地,跳频序列族U关于平均汉明相关界是最优的。
证明 由Sa( U)和Sc( U)的定义可知
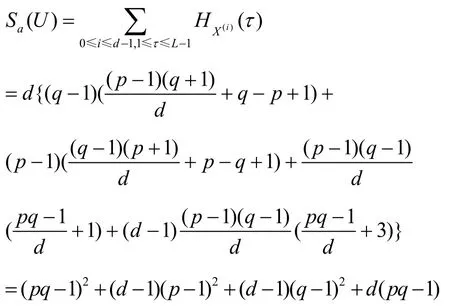
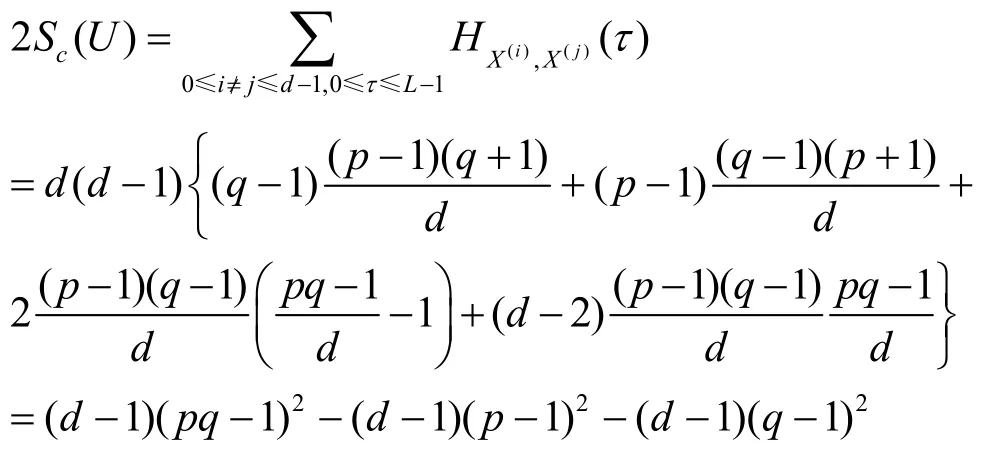
由平均汉明自相关和平均汉明互相关的定义可得式(9)和式(10)。把式(9)和式(10)代入式(4)可得:

5 结束语
较之达到最大汉明相关界的跳频序列族, 具有最优平均汉明相关界的跳频序列族的研究成果要少得多。在文献[12]的基础上,本文给出了Whiteman广义分圆类的一个推广,并且基于推广的Whiteman广义分圆类构造了新的跳频序列族,证明了新构造的跳频序列族关于平均汉明相关界是最优的。
[1] FAN P Z, DAMELL M. Sequence Design for Communications Applications[M]. London: Research Studies Press, 1996.
[2] WIN M Z, SCHOLTZ R A. Ultra-wide bandwidth time-hopping spread-spectrum impulse radio for wireless multiple-access communications[J]. IEEE Transactions on Communications, 2002,48(4):679-691.
[3] LEMPEL A, GREENBERGER H. Families of sequences with optimal Hamming correlation properties[J]. IEEE Transactions on Information Theory, 1974, 20(1): 90-94.
[4] PENG D Y, FAN P Z. Lower bounds on the hamming auto- and cross-correlations of frequency-hopping sequences[J]. IEEE Transac-tions on Information Theory, 2004, 50(9): 2149-2154.
[5] PENG D Y, et al. The average Hamming correlation for the cubic polynomial hopping sequences[A]. IEEE IWCMC 2008, International Conference on Wireless Communications and Mobile Computing[C].Crete, Greece, 2008. 464-469.
[6] CHU W S, COLBOURN C J. Optimal frequency-hopping sequences via cyclotomy[J]. IEEE Transactions on Information Theory, 2005,51(3):1139-1141.
[7] KE P H, ZHANG S Y. Frequency-hopping sequences based on d-form functions[J]. The Journal of China University of Posts and Telecommunications, 2010, 17(4): 58-62.
[8] DING C S, YANG Y, TANG X H. Optimal sets of frequency hopping sequences from linear cyclic codes[J]. IEEE Transactions on Information Theory, 2010, 56(7): 3605-3612.
[9] GE G N, MIAO Y, YAO Z X. Optimal frequency hopping sequences:auto- and cross-correlation properties[J]. IEEE Transactions on Information Theory, 2009, 55(2): 867-879.
[10] ZHANG Y, KE P H, ZHANG S Y. Optimal frequency-hopping sequences based on cyclotomy[A]. ETCS 2009, First International Workshop on Education Technology and Computer Science[C]. Wuhan, China, 2009.1122-1126.
[11] 刘方, 彭代渊.一类具有最优平均汉明相关特性的跳频序列族[J].电子与信息学报, 2010, 32(5): 1257-1261.LIU F, PENG D Y. A class of frequency-hopping sequence family with optimal average Hamming correlation property[J]. Journal of Electronics and Information Technology, 2010, 32(5): 1257-1261.
[12] LIU F, et al. Construction of frequency hopping sequence set based upon generalized cyclotomy[EB/OL]. http://arxiv.org/abs/1009.3602,2010.
[13] MEIDL W. Remarks on a cyclotomic sequence[J]. Designs, Codes,and Cryptography, 2009, 51: 33-43.
[14] PENG D Y, PENG T, FAN P Z. Generalized classof cubic frequency-hopping sequences with large family size[J]. IEEE Proceedings on Communications, 2005,152 (6): 897-902.
[15] PENG D Y, et al. A class of optimal frequency hopping sequences based upon the theory of power residues[A]. SETA 2008,Proceedings of the 5th International Conference on Sequences and Their Applications[C]. Lexington, KY, USA, 2008. 188-196.
[16] WHITEMAN A L. A family of difference sets[J]. Illinois Journal of Mathematics, 1962, 6: 107-121.
