利用移动内点来修复传感器网络空洞的算法

杨凯，刘全，张书奎,2，李瑾，翁东良

(1. 苏州大学 计算机科学与技术学院，江苏 苏州 215006；2. 南京大学 计算机软件新技术国家重点实验室，江苏 南京 210093)

1 引言

无线传感器网络是当前研究的热点，通过向目标区域部署大量价格低廉、具有移动、感知和通信能力的传感器节点构成的无线传感器网络，可广泛应用于军事、交通、医疗和救灾等领域。随着电子技术的不断发展，传感器节点的功能不断增强，体积不断缩小，使得利用无线传感网络完成对某一区域的监测成为可能。但是由于节点部署不均匀、环境外力影响或电量耗尽等因素而产生感知区域大型空洞，影响感知信息的精确性或降低通信的效率。因此，如何探测这些空洞区域，并对之进行修复成为传感器网络研究的重要内容之一。

空洞修复算法包括2部分：空洞探测和空洞修补。在空洞探测方面，文献[1]提出一种使用Voronoi图来发现空洞。文献[2]提出了 K覆盖(K-coverage)算法，使用计算几何中覆盖弧的相关性质进行空洞探测。在空洞探测中很少研究以地理信息作为辅助[3～6]。在空洞进行修复时，借助地理信息较多。文献[7～9]中，作者利用网格对传感器网络进行划分，部分文章使用地理信息进行空洞修复。文献[10]使用节点之间洪泛信息方式对空洞进行探测，只需要节点之间的相对位置。文献[3]使用移动节点获得不精确位置信息。文献[4～6]使用相互通信方式来确定节点位置，同样需要地理信息、GPS等设备的支持，对于大规模传感器网络来说成本昂贵，并且空洞修复问题本身就是一个NP问题， 使用地理信息仅仅将解决问题的精度提高，仍不能得到最优解。本文不借助地理信息，通过传感器节点所具有的感知、通信功能来获得不精确定位信息，利用这些不精确的地理信息确定空洞区域，并作为修复空洞的基础。

针对空洞修复问题，可有多种方式。文献[3]通过向传感器网络添加新的节点来完成空洞修复，并且提出了算法修复原则：1)加入新节点不会使空洞分裂；2)加入新节点至少能消除一段覆盖弧。文献[11]提出了一种移动空洞边缘节点以减小空洞面积的算法VHR(vector based hole recovery)，该算法基于一种假设条件，即密集分布的无线传感器网络中，传感器节点具有一定的移动能力，网络初始化时分布节点所形成的空洞面积较小，也是非连续的，VHR算法借助GPS提供的地理信息确定空洞边缘节点向空洞方向移动，在不改变已有覆盖的前提下缩小空洞面积，但是该算法只能应用于某些特定形状的空洞而且需要借助GPS，能量消耗较大。文献[5]提出一种使用Voronoi图作为解决空洞覆盖的方法，该方法重新布置传感器网络的节点，最大效率利用节点覆盖，使用Voronoi图对传感器节点进行迭代计算，但该方法需要节点之间精确的地理信息和额外的GPS设备。

本文提出一种不需要地理信息的基于移动的空洞修复算法SOI(search optimistic inner)，以文献[4,5,11]中节点可以具有一定的移动能力为理论支持，其中文献[3]移动部分节点用于覆盖空洞边缘节点未覆盖弧，文献[3]移动空洞边缘节点朝空洞方向移动，文献[4]移动节点以填补失效节点的感知范围。本文通过移动一些特殊节点，达到使感知范围覆盖整个目标区域的目的。在空洞探测阶段，使用文献[2]中的K-coverage算法进行探测，若目标区域为完全覆盖，算法的后续部分不进行，否则进入空洞修复阶段。SOI算法与文献[11]相比，虽然修复的精度有所降低，但不需要增加GPS设备，实施代价较小。与文献[3]相比，SOI算法不需要增加新节点，只需要移动部分节点就可以完成修复工作，尽管算法要求具有移动能力的节点提高了网络构建代价，但算法过程中移动节点数量和移动距离较小，其代价也是可以接受的。本文主要贡献如下： 1)提出基于移动的空洞修复准则，并引入相关定理；2)提出基于移动内点的空洞修复算法SOI。该算法在没有精确的地理信息时，寻找空洞边缘节点的最佳位置，最终通过移动完成修复工作。

2 问题描述

2.1 前提假设

无线传感器网络中，每一个节点都有唯一标识号(ID)，节点之间都可以正确地标识自身。每个节点都可以感知某一区域并与相邻节点进行通信，假定其感知和通信范围都为圆形，其感知圆与通信圆的半径分别为SR与TR。假定TR ≥ 2 ×SR (相关证明由Bejeranp Y完成)，这样网络的连通问题就等价为覆盖问题，一个K覆盖的网络一定是连通的。另外，传感器网络中传感器节点没有精确的地理信息，边界区域的节点都能够正确标识自身，不会将监测区域的边界误判为空洞。同时，由于节点是随机分布，假定3个节点的感知圆相交于同一点的概率为0，并且没有任意2个传感器节点位于同一个位置。

目前，大多数空洞修复的研究都是以网络连通为前提，且覆盖空洞是闭合的。本文同样是基于网络连通的，但对于空洞是否闭合没有特定的要求。本文假定每个节点都具有一定的移动能力，在目标区域随机分布节点后，通过节点的有限移动，每个节点可以获得其邻居节点的位置信息。以这些信息为基础，运行空洞探测算法可以有效探测出覆盖空洞位置与大小。由于研究的复杂性，本文只关注覆盖空洞修复问题，空洞探测方面使用文献[2]中K覆盖算法来探测空洞大小和位置。

2.2 相关术语

定义1 空洞边缘交点。如果2个节点都是空洞边缘节点，且它们之间互为邻居节点，那么这2个节点感知范围相交，处于空洞相交区域的节点为空洞边缘交点。在图1中P1为A节点与B节点的空洞交点，P2为B节点和C节点的空洞交点。

图1 空洞示意

定义2 内点。如果若干个节点都是邻居节点，那么一个传感器感知范围内的一点(不在该传感器感知范围的边缘上)是其他2个传感器感知区域的交点，则该交点称为内点。几何学上的定义是：3个圆U、V、W其半径为r，若P∈(Cv∩Cw)，P满足P∈Du，d( p, u)＜r则P为圆U内点。在图2中P3是传感器节点C和B的感知区域的交点，并且P3处于传感器A的感知范围内。

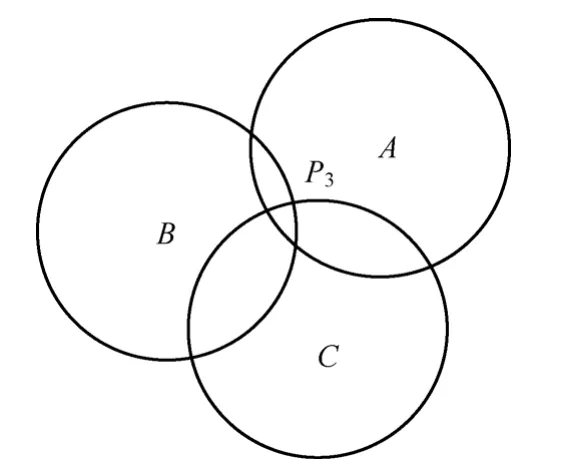
图2 空洞边缘节点，邻居节点示意

定义3 空洞内点。根据内点定义，在特殊情况下如果A为空洞边缘节点，那么P3为空洞内点。

定义4 空洞边缘弧。相邻的空洞边缘交点通过圆弧相连，节点感知区域边缘上连接空洞边缘交点的圆弧称为空洞边缘弧。

定义5 空洞边缘邻居。在传感器网络中如果有2个节点互为邻居节点，并且这2个节点为空洞边缘节点，则称这2个节点互为空洞边缘邻居。

在本文中有如表1所示的符号。

表1 相关符号定义

图3 覆盖弧

对于覆盖弧，有如下性质。

性质1 覆盖弧Su,v与Su,w相交，当且仅当μu,w+μu,v＞2×∠v, u, w。

性质2 覆盖弧Su,w⊂Su,v，当且仅当μu,w≥μu,v+2×∠v, u, w。

性质3 覆盖弧Su,w∩Su,v≠NULL ，且Su,w⊄Su,v，Su,v⊄Su,w。

性质4 覆盖弧Su,x⊂Su,w∩Su,v，当且仅当满足以下条件：

1) ∠v,u,x+∠x,u,w=∠v,u,w；

2) μu,x/2＜μu,v/2+∠v,u,x；

3) μu,x/2＜μu,w/2+∠w,u,x。

2.3 问题描述及相关性质

在空洞修复过程中，本文采用移动空洞边缘节点的方式进行空洞修复。通过不断移动空洞边缘节点减少网络中感知圆的重叠面积，扩大网络覆盖面积，最终达到消除覆盖空洞的目标。在空洞修复过程中，引入以下准则：1)移动节点不会使其邻居节点产生新的未覆盖弧；2)移动节点必须减少覆盖空洞的面积。由于节点是随机布置的，每个节点的感知圆与周围邻居节点的感知圆不规则相交，产生若干重叠的感知区域，在节点移动的过程中，需要遵循上面提出的2个准则。

利用移动节点来修复空洞，其本质是移动空洞边缘节点至某一位置使该节点的感知圆恰好经过内点，即节点的感知圆和其2个邻居节点相交于一点。这样节点间的冗余面积减小，节点覆盖面积增大。然而，由于节点分布的随机性，一个节点必然含有多个内点，需要从这些内点之中选择出一个作为移动后3个感知圆的交点。

简单网络模型中空洞边缘节点S的内点是有限的，从中选择一个距离S最远的内点，移动S，使S与其邻居节点相交于该内点即可完成空洞修复。但是由于传感器节点是随机分布的，S中内点位置非常复杂，不能简单的从中选择出一个距离S最远的内点。如图4所示，若S为空洞边缘节点，A、B、C都是S的邻居，由2.2节定义可知P1、P2、P3、P4为S的内点，按照现有的方法，选择距S最远的内点P1作为移动的内点，那么移动之后，虽然S与A、B、C的重叠面积减小了，但没有减至最小，S可以再次移动。但是再次移动的计算过程极其繁琐，而且移动之前必须使用空洞探测算法确定新产生的空洞。这里，关于内点可以有以下所述性质。

图4 复杂网络中的拓扑结构

引理1 如果一个圆的某个内点也是其他圆的内点，那么该内点的覆盖度大于同一圆的其他内点。

证明 假设有4个圆u、v、w、x，其圆周为Cu、Cv、Cw、Cx，并令SR=R，从条件可得∃p∈cv∩cw，dp,v=dp,w=R 且p∈cu∩cx，p为内点且q∈(Du∩Dv∩Dw∩Dx)。根据题设∃q∈cv∩cw且满足q∈Du，则q为内点且满足q∈(Du∩Dv∩Dw)。若根据本文算法移动圆u，则内点p永远会处于某个圆的范围中，其覆盖度一定大于其他内点，而q不满足q∈(Du∩Dv∩Dw)。证毕。

根据引理1，空洞边缘节点中选择被其他节点覆盖的内点作为移动的定位点，并不能使空洞边缘节点与其邻居节点的重叠面积最小(因为移动后的内点的覆盖度仍大于其他内点)。因此在选择内点时应该排除这一类特殊的内点，这里使用覆盖弧的性质来解决这一问题，并且本文把这一类空洞边缘节点的内点并且也是其邻居节点的内点称为覆盖内点。如图4所示，P1、P2、P4都是覆盖内点，以其中之一作为移动的定位点都会使移动算法修复空洞失败。

定理1 若圆v、w 在圆u形成的覆盖弧满足Su,w⊂Su,v，那么圆w产生的内点p满足p⊂Dv。

证明 3个圆u、v、w的覆盖范围为Du、Dv、Dw，所形成的覆盖弧为Su,v、Su,w且满足Su,w⊂Su,v。假设p1、p2∈Du∩Dv且du,p1=du,p2=R 。q1、q2∈Du∩Dw且du,q1=du,q2=R ，由Su,w⊂Su,v可知在Du上，故可得(Du∩Dw)⊂(Du∩Dv)，那么由Du∩Dw所产生的内点p均有p∈Du覆盖，其产生的内点也为覆盖内点即存在内点p满足p⊂Dv。证毕。

根据定理1，在进行内点选择过程中节点会产生如图5(c)的情况，那么此时应具体去考虑此种状况。如果Su,x⊂Su,w∪Su,v，v、w、x 3个感知圆相交，x产生的内点可能会被v和w所覆盖，那么要进行下一步判断，这里对x分为如下2种情况。

图5 覆盖弧性质

1) 如果Sx,w∩Sx,v=NULL，那么x所产生的内点均被覆盖；

2) 如果Sx,w∩Sx,v≠NULL，那么x不是覆盖内点。

定理2 在圆u中若存在Su,x⊂Su,w∩Su,v，且Sx,w∩Sx,v≠NULL ，则x在u中的内点均被覆盖。

证明 由覆盖弧Su,v、Su,w、Su,x可得cu∩cv产生的弧为，cu∩cw产生的弧为，cu∩cx产生的弧为，由Su,x⊂Su,w∪Su,v可知。由Sx,w∩Sx,v≠NULL ，可知Sx,w与Sx,v覆盖弧是连续的，并且则 ∃p∈(cu∩cx)均有p∈(Dw∪Dv)，根据定理1的结论(cu∩cx)⊂(cu∩cw)∪(cu∩cv)，所以x产生的内点p有p∈(Dw∪Dv)。证毕。

结合引理1、定理1和定理2可以逐步剔除已经被覆盖的内点，最后从剩下的内点中选择出一个距离空洞节点最远的作为最佳内点。本文提出了一个寻找最佳内点的算法（SOI）。

3 算法描述

本文提出了一种利用移动内点来修复空洞的算法，其中包括节点移动方向和内点选择算法。由于算法没有精确的地理信息，需要使用一种特殊的方式来确定节点移动方向。每一个节点在确定自己是空洞边缘节点时都会自动运行该算法，通过计算移动方向和移动距离将自身移动到新的位置。

3.1 移动方向

本文通过移动空洞边缘节点修复空洞，首先应确定空洞边缘节点的移动方向，这里节点选择朝未被覆盖的弧方向移动，能够减少空洞的面积。如图6(a)所示节点S为空洞边缘节点，P1、P2为空洞边缘交点，弧为节点S的未覆盖弧，做向量、则+得到向量，由图6(a)可知指向未覆盖弧中点且朝向空洞的方向，沿着移动无线传感器节点S必然会减小空洞的面积，使得S与其邻居A、B的传感圆的重叠面积缩小。需要指出的是，在确定移动方向时，可能存在例外情况，如图6(b)所示，通过计算空洞边缘节点S与邻居所形成的空洞边缘交点、的向量和，得到一个向量，但不能把作为节点移动的方向，因为沿移动只能加大空洞边缘节点与其邻居节点的重叠面积，相反地应采用为节点移动方向。

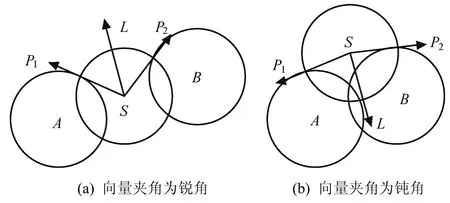
图6 节点移动方向的确定

移动节点的目的是减小空洞面积，从移动的本身来看移动增大了空洞边缘节点未覆盖的弧长，最终会使得尽可能多的节点感知圆相交于同一点。本文2.1节中提到3个传感器节点的感知圆相交于同一点的概率为0，并且任意2个传感器节点都不会位于同一个位置，本文算法的本质是移动空洞边缘节点使节点与其邻居节点相交于同一点。由于无线传感器网络中节点是随机分布的，没有精确的地理信息，故使用向量是不现实的。本文提出一个不精确的移动轨迹作为空洞边缘节点的移动方向。

如图7所示，S为空洞边缘节点，A、B为S邻居节点，且A、B恰为S空洞边缘节点（在SOI算法中A、B为覆盖弧序列中，2个相邻但覆盖弧不相交的节点），做AB的垂线经过S且指向S的向量，根据2.3节已知A、B的位置A（ds,a,qa）、B（ds,b,qb） 计算出S的移动轨迹为：

1) 如果cos∠SAB＞0，移动轨迹σs=-θA+∠SAB+2k×π；

2) 如果cos∠SAB＜0，移动轨迹σs=-θA-∠SAB+2k ×π，且

图7 空洞边缘节点移动轨迹

3.2 SOI算法与计算移动距离

在这一部分中，算法从空洞边缘节点内部选择一个内点作为移动的终点，并计算节点移动的距离。根据2.3节中内点性质提出了一个选择最佳内点的算法（SOI算法）。

当一个节点u被空洞探测算法计算为空洞边缘节点时，运行下述算法(SR=r)。

Step1 扫描u周围邻居节点构造一个分割弧队列Qall，Qall中成员为逆时针遍历的邻居节点。

Step2 遍历Qall，删除每一个x当且仅当覆盖弧Su,x⊂Su,v(v、x为队列中任意邻居节点标记)。

Step3 遍历Qall，删除每一个x当且仅当覆盖弧Su,x⊂Su,w∪Su,v且Sx,v∩Sx,u≠NULL，这样得到一个队列。

Step5 从Qn中取相邻2个节点n1、n2令ni=n1，nj=n2。

Step6 若覆盖弧Su,i∩Su,j=NULL 保存i和j，此时i和j为空洞邻居节点，计算节点移动的方向σm。ni=nj，nj=nj+1，转向Step6，否则转向Step7。

Step7 计算ni、nj感知圆产生的交点o距u的距离，并选择其中较小的值Li,j保存，令ni=nj，nj=nj+1，如果nj=n1转向Step8，否则转向Step7。

Step8 选择出max(Li,j)，并保留产生该交点的2个无线感知器节点ni，nj的相关信息。

Step9 以max(Li,j)，σm为条件根据图8所示，计算出节点在移动方向上移动的距离L。

图8 计算内点距空洞边缘节点距离，s为空洞边缘节点，u和v为队列中满足条件节点

在上述算法中，逆时针扫描每一个空洞边缘节点的邻居节点，根据内点性质，剔除产生覆盖内点的邻居节点，剩下的内点组成一个队列Qn。计算Qn中节点产生的内点，选择其中距离空洞边缘节点最远的内点为最佳内点。这样算法能同时满足空洞修复的2个准则，不会产生新的空洞，也能够使节点冗余面积最小。接下来是算法计算节点移动距离。

计算内点与空洞边缘节点距离的算法实现：

u和v满足Ss,u∩Ss,v≠NULL ，则u和v的交点为s的内点，设其交点为o。ds,u、ds,v、du,v已知，且du,o=dv,o=r 。由三角法则得

由于

由式(1)～式(4)可以求出

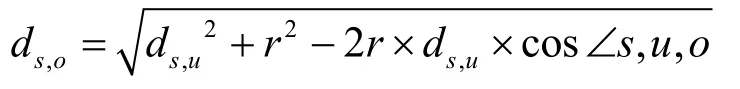
ds,o有2个值取ds,o＜r即可，Lu,v=ds,o，最后取max(Li,j)，并求出o的相对于s的位置＜ds,o,θs,o＞这即是所求的最佳内点。确定最佳内点后，进行算法最后一步，移动空洞边缘节点至最佳位置。

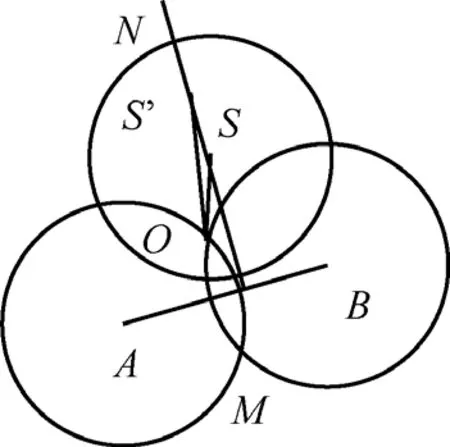
图9 移动空洞边缘节点S至S '

算法表明，节点的移动限制在1跳的距离内。而且节点的移动没有影响现存覆盖，没有对初始时节点的覆盖度产生影响，所以算法并未对原始覆盖产生影响。设空洞边缘节点的数量为n，则算法时间复杂度为O( n2)，在修复过程中空洞边缘节点按ID顺序依次进行修复，能够快速收敛。尽管在修复过程中空洞边缘节点不可能全部移动到最佳位置，但经实验证明在密集网络中，它仍然能够到达1覆盖。

4 仿真实验

本节讨论SOI空洞修复算法的性能，使用节点移动的总距离和修复空洞所占面积的百分比来评估算法性能，同时与文献[3]中VHR算法进行比较。VHR算法采用移动节点的方式，将空洞边缘节点沿着向量方向移动一定距离，逐渐缩小覆盖空洞面积。其中向量由边界缺口点来决定，只有缺口点向量的角度小于π时节点才能移动，而节点移动距离由邻居节点和协作节点共同决定。该算法能够保证在不会破坏已有覆盖的条件下，尽可能缩小空洞面积。

4.1 仿真实验设置

仿真实验采用C++完成算法，算法在一个400×400的矩形区域中随机部署n个传感器节点，节点的感知半径为20(其传输半径为40)，节点的个数随实验的进行不断变化。为了简化问题，仿真实验并没有实现节点通信的下层MAC协议，也没有关注节点在通信和移动过程中所产生的能量消耗，而是通过空洞修复算法中节点移动的总距离来衡量算法过程中的能量消耗。在算法过程中，首先对目标区域随机分布的节点进行空洞探测（使用Bejeranp Y的K-corerage算法），如果节点为空洞边缘节点则保存其ID，否则检测下一个节点。空洞探测结束后，空洞边缘节点按照 ID顺序依次进行修复，待所有节点执行完毕后算法终止。

在SOI算法中，空洞边缘节点按ID顺序进行移动，节点的移动只会对周围空洞邻居节点的修复产生影响并不会扩大到整个网络，并且在节点密集分布的网络中有限几个节点的移动会完全修复空洞，使得其他空洞节点运行SOI算法时在计算移动轨迹时自动退出，并不影响算法有效性。

4.2 实验结果分析

为了说明空洞修复算法中节点的移动方向，标记出节点的移动方向。图10(a)中显示的是n=30时，节点随机分布所形成的拓扑结构。为了使实验更为完整，设定传感区域边缘的节点不参与空洞修复，以避免移动区域边缘节点产生新的空洞。图 10(b)是运行修复算法时，每个空洞边缘节点的移动方向，图中箭头为修复算法中节点的移动轨迹。由于SOI修复算法中没有精确的地理信息支持，只能通过2个空洞边缘邻居与空洞边缘节点共同确定节点移动方向，这种移动方向是不精确的，但后续实验表明，在节点密集分布的网络中这种粗糙的移动可以获得不错的效果。

如图11所示，本文分析了在目标区域中分布不同数量的节点时，运行空洞修复算法前后覆盖区域占目标区域的百分比。初始时，目标区域的覆盖率随着分布节点数量的增多不断提高。移动前后目标区域覆盖比率的变化表明修复后覆盖区域明显扩大，并且随着节点数量增多传感区域的覆盖面积增大，空洞面积相应减小，使用SOI修复算法的效果也越好。在节点数量较少时可移动的节点数量很少，导致移动后空洞修复效果不明显。随着节点数量增加，可移动节点也增多，使用移动修复的效果也更明显。与 VHR算法相比，在密集网络中 SOI算法的性能稍好于VHR算法，并且SOI算法不需要精确地理信息，算法适应性要好于VHR算法。

图11 节点移动前后覆盖比率

图12显示了无线传感器节点数量与空洞面积之间的关系。可以看出，节点数量越大，产生空洞的面积越小。在实验过程中，因为节点是随机分布的，所以在节点数量相同的条件下，每次实验中所产生的空洞也有差异，这里的空洞是 10次实验的结果取平均值。该图表明，在实际应用中，有限区域内密集布置的无线传感器网络所形成的空洞面积比率很小，这样空洞修复算法仅仅只需要移动有限节点就可以完成对目标区域的完全覆盖，可以确保无线传感器网络中节点能量不会因为移动消耗大量的能量。

图12 无线传感器节点数量与空洞面积的关系

本文提出的修复算法是基于节点移动，所以空洞修复算法中节点移动总距离是考查修复算法的重要条件。在无线传感器网络中，节点的能量是有限的，移动会消耗传感器节点大量能量，一旦网络中的节点因为移动消耗过多的能量，必然会产生新的空洞。因此，为了延长节点在无线网络中的生存时间，平衡网络中的负载，算法需要尽可能地减少移动所产生的能量消耗即减少移动式空洞修复算法中节点移动的距离。由于在空洞修复算法中，不同的修复算法之间因为修复的方式不同，很难比较各种方法的优越性，因此本文中只与同为移动式的VHR算法进行比较。图13中详细描述了在节点数目不同的情况下，SOI修复算法移动传感器节点的总距离与 VHR算法移动距离之间的比较。从图中可以看到，节点数目越大所需要移动的距离越小，因此上文中提到的修复算法的有效性得到证实。

图13 SOI算法与VHR算法移动距离对比

如图13所示，节点数量较少时，SOI移动距离要大于VHR，这是因为在节点稀疏分布的网络中，与 VHR算法相比，SOI算法中每一个非边界的空洞边缘节点都参与移动，并且SOI算法不考虑移动节点与1跳范围内的协作节点之间的关系，也没有使用向量来精确表示移动方向，大多数节点的移动距离比VHR算法大。但是当节点数量超过800时SOI修复算法移动的距离要小于VHR算法。这是因为在密集网络中，SOI修复算法的特点是尽可能地去移动节点，减少无线传感器节点之间重叠面积，而 VHR算法中节点更多地考虑保持与协作节点之间的距离和精确地移动，所以在这种情况下，SOI算法仅仅需要移动几个节点就可以完成空洞修复任务，此时SOI算法移动节点的距离要小于VHR算法。

如图14所示，在修复空洞时，与VHR算法相比SOI算法需要移动更多的节点。在VHR算法中，只有向量夹角为锐角的节点才能移动，而SOI算法大部分非边界区域的空洞边缘节点都可以移动，所以 SOI算法中可移动的节点数量要明显大于 VHR算法。尽管如此，由于SOI算法所选择的移动方向是粗糙的，在稀疏网络中，SOI算法的移动距离要明显大于 VHR算法。空洞修复过程中，移动节点需要消耗一定能量，但如图14所示SOI算法移动节点的数量远小于节点总数量，移动总距离也较小，并且网络中的每个节点不需要额外的 GPS设备，故该算法虽然消耗一定能量，但从整体上来说也是可以接受的。

图14 SOI算法和VHR算法移动节点数量对比

本文算法是基于二维空间的，也可以将其扩展到三维空间，这样计算内点就扩展为计算空间球体相交的弧切面，SOI算法的目标也可以演变为让多个传感器节点的弧切面相交即可。这里覆盖内点的概念也可以扩展到空间中的面，进一步讨论三维空间中的覆盖问题。

5 结束语

覆盖问题是无线传感器网络的重要研究问题。在前期的研究工作中，主要依靠在无线传感器网络中布置大量冗余节点来解决完全覆盖的问题。本文针对传感器网络覆盖问题，证明了网络覆盖中几个基于覆盖性质的定理。基于这些定理，以及在没有地理信息的支持下，针对密集分布的无线传感器网络中空洞修复问题，提出了空洞修复算法SOI。该算法计算出空洞边缘节点的移动方向和空洞边缘节点移动的最佳位置，通过移动减小节点感知圆之间冗余面积扩大节点的覆盖面积，以此实现传感器网络中的空洞修复。实验表明，该算法在节点密集分布时移动所有的空洞边缘节点以较小的移动距离获得良好的空洞修复性能。本文的下一步工作重点是在没有地理信息系统的支持下提高修复稀疏网络的精确度。

[1] WANG G, CAO G, LA P T. On solving coverage problems in a wireless sensor network using voronoi diagrams[A]. Proceedings of the International Workshop on Internet and Network Economics(WINE)[C].HongKong, 2005. 584-593.

[2] BEJERANP Y. Simple and efficient k-coverage verification without locatioan information[A]. Proceedings of the IEEE Conference on Computer Communications[C]. Phoenix, 2008. 291-295.

[3] 苏瀚，汪芸. 传感器网络中无需地理信息的空洞填补算法[J]. 计算机学报. 2009, 32(10): 1957-1970.SU H, WANG Y. A self-healing algorithm without location in sensor networks[J]. Chinese Journal of Computers, 2009, 32(10): 1957-1970.

[4] SEKHAR A, MANOJ B S. Dynamic coverage maintenance algorithms for sensor networks with limited mobility[A]. Proceedings of the Pervasive Computing and Communications[C]. Hawaii, 2005.

[5] LI X, DAVID H. Distributed coordinate-free hole recovery[A]. Proc of GLOBECOM[C]. Beijing, 2006. 189-194.

[6] YOU J, LIECKFELDT D. Context-aware geographic routing for sensor networks with routing holes[A]. Proceedings of the Wireless Communications and Networking Conference[C]. Budapest, 2009. 1-6.

[7] BOYD, ALAN W. On the selection of connectivity-based metrics for wsns using a classification of application behavior sensor networks[A].Proceedings of the Ubiquitous, and Trustworthy Computing(SUTC)[C]. California, 2010.

[8] FYS L, CHIU P L. A near-optimal sensor placement algorithm to achieve complete coverage/discrimination in sensor networks[J]. IEEE Communications Letters, 2005, 9(1):43-45.

[9] NITIN K, DIMITRIOS G. Sensor network coverage restoration[J].CITESEER, 2008, 10(12): 21-24.

[10] KUN Y H, JANG P S. Hole detection and boundary recognition in wireless sensor networks[A]. Proceedings of the Indoor and Mobile Radio Communications[C]. Mannheim, 2009. 72-82.

[11] PRASAN K, JANG Z T. Vector method based coverage hole recovery in wireless sensor[A]. Proceedings of the Communication Systems and Networks (COMSNETS)[C]. Bangalore, 2010. 1-9.