基于Crossbar的可重构网络输入排队分域调度研究

张博，汪斌强，王珊珊，卫红权，李挥

(1. 国家数字交换系统工程技术研究中心, 河南 郑州 450002;2. 北京大学深圳研究生院 深圳市云计算关键技术和应用重点实验室，广东 深圳 518055)

1 引言

互联网基于资源统计复用、“尽力而为”服务模式的特点，辅以Overlay、CDN等技术拓展了其所承载的业务范围，一定程度上满足了规模化的音视频业务、安全业务等承载要求，但并未从根本上解决互联网面临的安全、多播、QoS等问题。其根本原因在于一方面网络是刚性的，网络的设计与构建依据特定业务需求进行，改造只能依靠升级和扩展，无法实现功能重构；其二节点是封闭的，节点的升级和扩展只能由原提供商实施，无法实现开放。从而导致了互联网的僵化问题。针对上述问题，摆脱传统网络技术体系束缚，提出了一种面向服务提供的柔性网络技术体系。

面向服务提供的柔性网络技术体系对现有和未来可能出现的用户业务进行科学聚类[1]，业务的聚类方法有多种，因应用环境不同而异，当前主要是通过业务对服务质量的要求进行聚类。还可以按照功能特征进行聚类，例如互联网上的业务可以分为视频、语音、交互式命令等。还可以按照通信方式的数量进行分类，将业务分为点到点业务、点到多点业务和多点到多点业务等[2]。

在柔性网络技术体系中，基础设施提供商建设、管理和维护物理网络基础设施，为可重构服务承载网(RSCN, reconfigurable service carrying network)提供网络资源。服务提供商在网络级，根据业务需求考虑异质和同质、成本和收益[3]和负载流量均衡[4]等因素实现RSCN优化构建。在节点级，通过重构将节点资源分割为某个RSCN独享，支持网络级承载网之间的独立运行。当某一业务取消时，该RSCN可立即拆除，将网络资源应用到新的RSCN构建中。

网络基础设施包括可重构路由交换平台、智能光节点和相关链路等，其中可重构路由交换平台是网络基础设施的核心。可重构路由交换平台中的交换结构作为业务时延、时延抖动、分组丢失率等特性主要的影响组件，具有更加重要的作用，可以通过对交换资源分割，使各RSCN独享交换资源，来满足业务对QoS的需求。如图1所示，R为可重构路由交换平台，S为对应的交换资源(包括缓存、调度、交换结构等)，综合管理接收用户需求，生成RSCN构建命令，下发给各个可重构路由交换平台，其中包括对交换结构的分割参数，可重构路由交换平台接收命令，通过重构，将交换资源分割给各个承载网，完成不同承载网之间交换资源的隔离。其中，为承载网1对应交换结构，为承载网2对应交换结构，为承载网3对应交换结构，其他为未使用的交换资源。

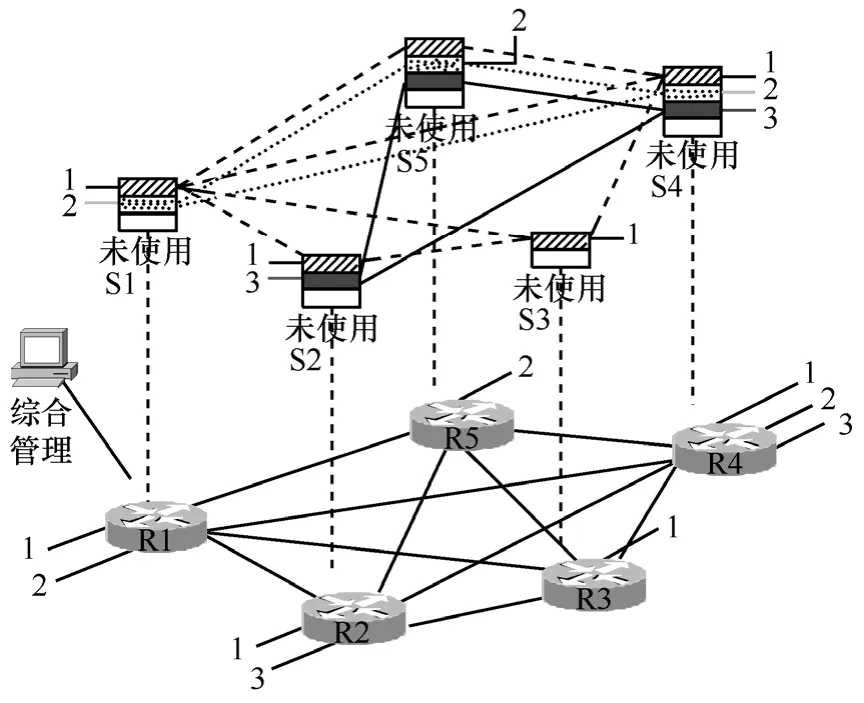
图1 可重构路由交换平台交换结构空分示意

本文在面向服务提供的柔性网络技术体系下，基于RSCN的构建，针对可重构路由交换平台中Crossbar交换资源，以8× 8Crossbar的分域为例引出了输入排队Crossbar交换结构调度问题，提出了一种分域承载组调度算法，该算法在单个承载组内进行轮询调度，域内进行最长队列优先调度，推导了组内和域内的调度过程。并在交换性能仿真平台SPES中进行了复杂度和时延特性的仿真，仿真结果表明：分域调度算法的调度复杂度小于不分域调度算法的调度复杂度，相对于传统典型的调度算法，分域承载组调度算法具有更优的时延特性。

2 交换结构分域原理

2.1 面向RSCN的交换结构需求

RSCN与虚拟网构建不同之处在于：网络环境和实现技术不同，虚拟网构建通过设备虚拟化的形式，选择和设置虚拟节点，连接虚拟节点间的虚拟链路，而RSCN构建基于可重构路由交换设备的柔性网络，通过设备的重构形式支持。构建拓扑不同，虚拟网拓扑和实际物理网络拓扑是分离的，而RSCN拓扑与实际物理网络拓扑是对应的。

在RSCN的构建中，网络资源可抽象表示为G( V, E)，其中，V表示物理节点的集合，E表示物理链路的集合，∀e∈E，c( e)表示链路e所能够承载的最大带宽。对于RSCN构建需求，可抽象表示为{Gv( Vv,Ev),D}，其中，Gv( Vv,Ev)表示RSCN的拓扑，Vv表示RSCN逻辑节点的集合，Ev表示RSCN逻辑链路的集合，D={dev|ev∈Ev}为逻辑链路ev的带宽需求dev的集合。RSCN构建问题可描述为将逻辑链路映射到物理路径，记作path( s, t)=Mlink(ev)，其中，s=Mnode(sv)，t=Mnode(tv)，path( s, t)表示s至t所经过的物理链路，Mlink(·)表示逻辑链路到物理路径的映射关系，Mnode(·)表示逻辑节点到物理节点的映射关系。RSCN构建是求解在G( V, E)中构建一个子图G′( V′, E′)，该子图满足：

且∀e∈E′，链路e上的带宽为

设f( e)表示链路e单位流量的带宽所需的费用，对RSCN构建的设计目标是构建子图G′( V′, E′)的费用最小化，如式(3)所示。

假设节点v'i∈V'的需求为{x11(e), x12(e),…,x1N(e);x21(e),…,x2N(e);…;xi1(e),…,xiN(e );…}，可转换为如图2所示的需求。

图2 节点构建需求

其中，{RSCNki,Cki}表示k号服务承载在第i个端口的带宽需求为Cij。在可重构路由交换平台中，SE(switching element)为交换组件，FE(forwarding element)为转发组件，LE(link element)为接口组件，其具体的实现方式见文献[5]。在SE中，采用Crossbar交换结构的IQ调度。

2.2 Crossbar结构分域

对于输入端口i，考虑到双向传输的需求，则第k个承载网在输入端口i的带宽需求Input( Cki)等于第k个承载网在输出端口i的带宽需求Output( Cki)。定义承载网输入矩阵为表示承载网在各输入端口的分布，其生成过程如算法1。

算法1 R生成过程

由M'=RTR得交叉开关匹配矩阵M为

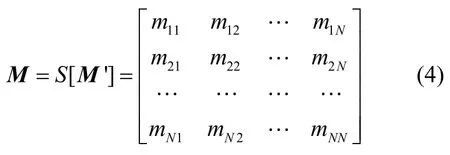
定义1 第n个调度域用SDn表示，满足SDn( Ir)数据分组不到达SDn'(Or)，且SDn'(Ir)数据分组不到达SDn( Or)，其中，SDn( Ir/Or)为第n个调度域的任意输入/输出端口。

对于一个N×N的Crossbar交换结构，为了更清晰的说明分域原理，选择N=8，如图3(a)所示。Crossbar交换结构内部无阻塞，如果无出端口竞争，可实现输入8个端口到输出8个端口的数据交换。假设该结构被平均分割给3个调度域，即每个调度域需要该交换结构端口数量为2、3和3。共有种分法。假设其中调度域1需求的输入端口为{1,4}，输出端口为{1,4}，调度域2需求的输入端口为{3,5,8}，输出端口为{3,5,8}，调度域3需求的输入端口为{2,6,7}，输出端口为{2,6,7}，如图3(b)所示，将每个交叉开关当作交换资源，平均分割成3个承载网调度域，其交换资源利用率为，因为有42个交叉开关在该分割周期内不再被控制，对该42个交叉开关进行关闭来实现分域调度。

假设N×N的Crossbar交换结构分割成n个端口数不等的承载网调度域，即n个承载网调度域，可用(N1, N2,…,Nn)来表示其占有的输入总端口数，满足N1+N2+…+Nn=N，则第i(1≤i≤n≤N)个调度域占用输入端口数为Ni。其Crossbar交换资源利用率为

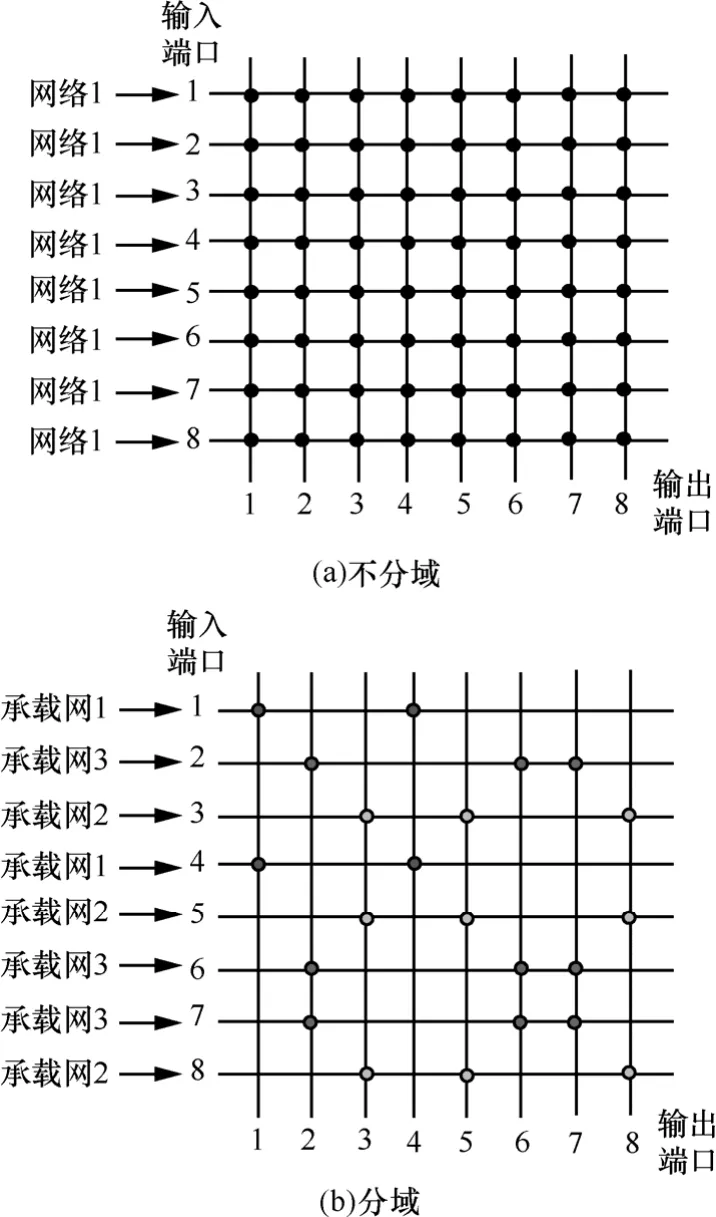
图3 8×8交换结构分域示意

对于Crossbar交换资源利用率nλ来说，当n=1时，λmax=1，为传统的无分域交换；当n=N时，，为N个点到点交换；当1＜n＜N时，，为分域交换。对于分域交换,当n=M0时，假设，共有种分域方式。通过分割成n个Ni×Ni, i=1,2,…,n 的调度域，减少单个调度域输入输出端口数，将集中式的N×N调度复杂度转换为Ni×Ni调度复杂度。

3 分域承载组调度算法

3.1 输入排队调度

在分组交换路由技术的发展上，交叉（crossbar）矩阵在N较小时是一类实现无阻塞的理想交换结构，它的调度过程是先由调度器对活跃输入端口进行无输出端口争用的配对，决定所有活跃输入端口下一个时隙的输出端口，而在下一个时隙进行传输。仅靠交换结构本身还无法实现无阻塞交换，必须与相应的缓存方式与调度算法相结合。输出排队（OQ）[6]调度，能够为业务提供100%吞吐量、速率及时延方面的QoS保证，但需要交换结构的加速比达到N，当N较大时是很难实现的。

比较而言，输入队列（IQ）调度，只需交换单元和存储单元工作在线速，采用虚拟输出排队（VOQ）机制解决队头阻塞问题。但输入排队交换结构的调度算法需要全局考虑交换结构所有输入端口和输出端口的带宽使用，因此必须采用集中式的调度机制，其本质是一个双向图的匹配求解问题。集中式的调度机制使得在输入排队交换结构实现服务质量保障十分复杂。已提出的如最大权重匹配调度算法已经证明可以提供100%的吞吐量，然而其复杂度为O( N3logN)[7]，很难具有现实意义。文献[8]致力于对最大权重匹配算法进行简化，但是其复杂度降低有限，依然无法在高速环境下应用。另一种思路通过利用输入排队交换结构双向图匹配特征，采用随机化思想[9]求解最大匹配的逼近匹配关系。但它仅从吞吐量单个方面优化调度性能，缺乏其他相关的服务质量保障措施。

虽然研究人员提出种种其他解决方案试图降低MWM（maximum weight matching）和MSM（maximum size matching）的实现复杂度[10,11]，然而不加速条件下，这种复杂度降低是以牺牲IQ交换结构性能为代价的。通过对基于Crossbar输入缓存调度的研究不难发现，影响缓存调度的一个关键因素是交换结构的输入输出端口数，如表1所示。

表1 输入排队调度算法复杂度与N的关系

为在复杂度和性能之间进行折中，研究人员逐步着眼于将基于时间戳和轮询的调度算法进行结合。GRR(group round robin)[12]引入一种流分组策略将大量流聚类为“流组”，并采用基于时间戳的WF2Q（worst-case fair weighted fair queuing)算法[13]作为组间调度算法，DRR(deficit round-robin)算法[14]作为组内调度算法，提高算法的公平性和降低复杂度。在组数较小的常量假设下，GRR能基于现有算法获得O(1)时间复杂度。当流速动态改变时，基于时间戳的调度策略无法提供恒定的GPS(generalized processor sharing)[15]相对时延。

FRR(fair round-robin)[16]组间采用基于时间戳的调度策略，组内采用轮询的调度策略，能为流组i提供端到端时延上限。不足之处在于其“摊还”复杂度，在传输前FRR算法需要将组内分组组装较大的“帧”，所以分组会经历O( K)的组装时延。

轮询调度算法RR/GPFQ(round-robin/goup packet fair queuing)[17]将基于分组的GPS算法进行改进以支持流速率的动态调整，降低了算法复杂度，并获得严格的时延上限，且能够提供时延和公平性特性。RR/GPFQ算法的时延和公平性上限仅取决于给定组内或组群的流状态，而不是分组数目N。

针对以上输入调度和分层调度的不足之处，本文针对可重构服务承载网构建的特殊性，采用分层调度的思想，将调度过程分为2层，如图4所示，第1层将单个RSCN对应一个调度组，进行承载组内调度(CGS, carrying group scheduling)；第2层进行组间的域调度(DS, domain scheduling)。

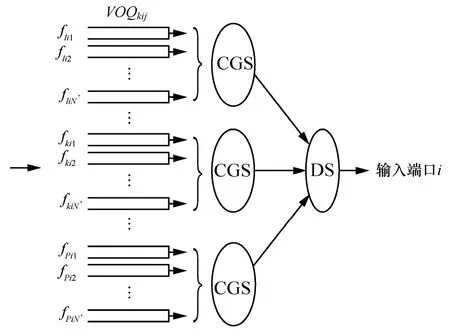
图4 承载组调度示意

其中，队列VOQkij缓存第k个承载网到达输入端口i、去往输出端口j的业务流fkij、N'为本调度域所包含的输入端口数。具体而言，首先根据P个承载网划分为P个承载组在每个承载组内采用改进的轮询机制决定组内数据分组的调度顺序。而后，DS采用基于最长队列优先的调度机制决定各调度顺序。

3.2 承载组内调度

针对本文承载组内调度借鉴文献[18]中SRR调度算法，对LDRRWA进一步改进，采用平滑的DRR调度策略(SDRR, smoothed DRR)。

在单个承载网内，用rkij标识fkij的带宽需求，用表示调度权重，如式(6)所示。

SDRR算法以“帧”组织一次轮询调度过程，具体如算法2。行1)将承载组共享份额计数器CG_deficit清“0”。行2)～16)对至少输出一个分组的流组成的链表acitve_list进行轮询输出，非空的流fijk将转移到链表acitve_list′中，以进行第2轮分组的共享份额轮询调度。如行17)～23)所示，该共享份额过程借用CG_deficit中份额来满足部分不能支持本轮分组输出的调度份额需求，出现负份额，在下一轮调度过程中，上次没有借用到份额的流优先借用。

算法2 SDRR调度过程

3.3 域调度

域调度采用最长队列优先(LQF, longest queue first)的调度方法，记为DSLQF。如图3(a)所示，对于一个8× 8的无分割交换结构，二分图匹配下的8× 8匹配矩阵表示为M(n)，其中，元素mij( n)表示第n时隙内输入端口Ii( i=1,2,…,8)到输出端口Oi( i=1,2,…,8)的交叉开关的状态。

DS1可以表示为

DS2可以表示为

DS3可以表示为

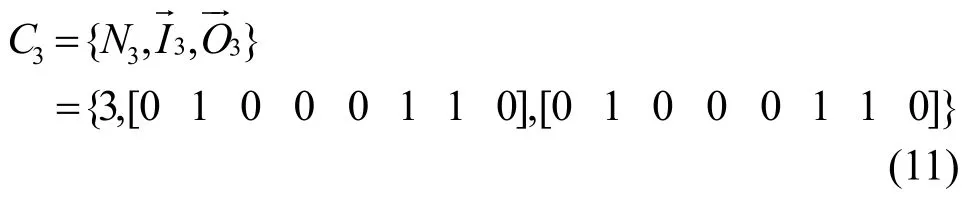
二分图匹配下的8× 8匹配矩阵为

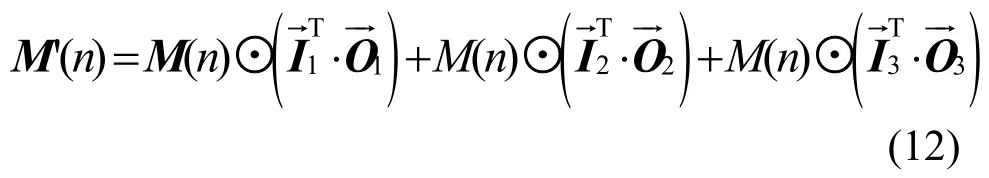
其中，⊙为Hadamard积[19]。

其中，mkij(n)表示第n时隙内第k( k=1,2,3)个SD输入端口Ii( i=1,2,…,8)到输出端口Oi( i=1,2,…,8)的交叉开关的状态。

对于基于队长的调度算法，相应变化的有队长矩阵、状态矩阵和到达矩阵。其匹配矩阵由8× 8变为了N×N，假设其分割为W个SD，分别为

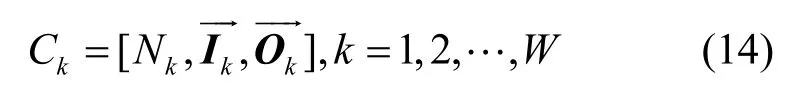
则其匹配矩阵为

无分割队长矩阵L( n)表示为

其中，元素lij(n)表示第n时隙内输入端口Ii( i=1,2,…,N)到输出端口Oj(j=1,2,…,N)的VOQij队列队长，行向量-L→i(n)是输入端口Ii的队长向量，列向量(n)是输出端口Oj的队长向量。

有分割队长矩阵L'( n)表示为

无分割到达矩阵A(n)表示为

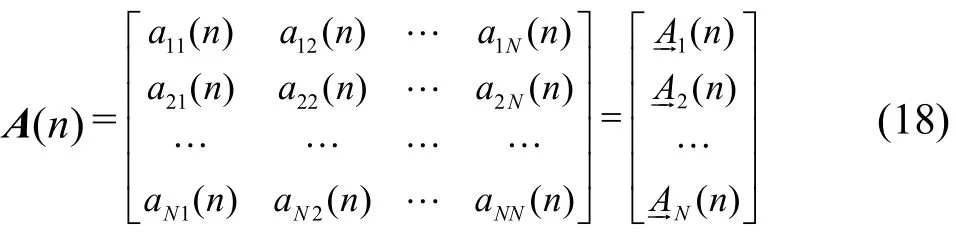
其中，元素aij(n)表示第n时隙内输入端口Ii( i=1,2,…,N)到 输 出 端 口Oi( i=1,2,…,N)的VOQij队列到达过程，行向量(n)是输入端口Ii的到达向量。在容许流量模型下，需满足条件

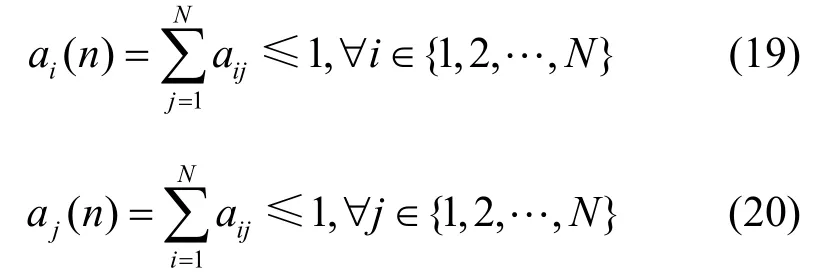
有分割到达矩阵A'(n)表示为

在容许流量模型下，需满足条件

交换结构队长矩阵迭代过程[20]为

无分割状态矩阵Q(n)为

其中，元素mij( n)表示第n时隙内输入端口Ii( i=1,2,…,N)到输出端 口Oj(j=1,2,…,N)的VOQij队列中信元的有无。

其状态矩阵Q(n)迭代过程为

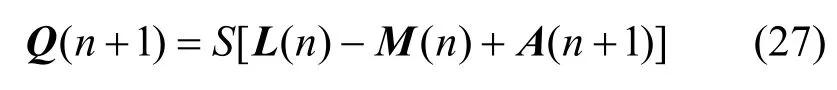
有分割状态矩阵Q'(n)为

DS调度过程描述为

步骤1 调度器获得交换结构分割参数Ck=同时令n=1,P=1,L'(0)=M'(0)=A'(0)=Q'(0)=[0]。

步骤2 在时隙n中有信元到达，状态矩阵Q'( n)发生变化，qkij向其调度器发出请求，输入端口Ii形成到达行向量(n)。

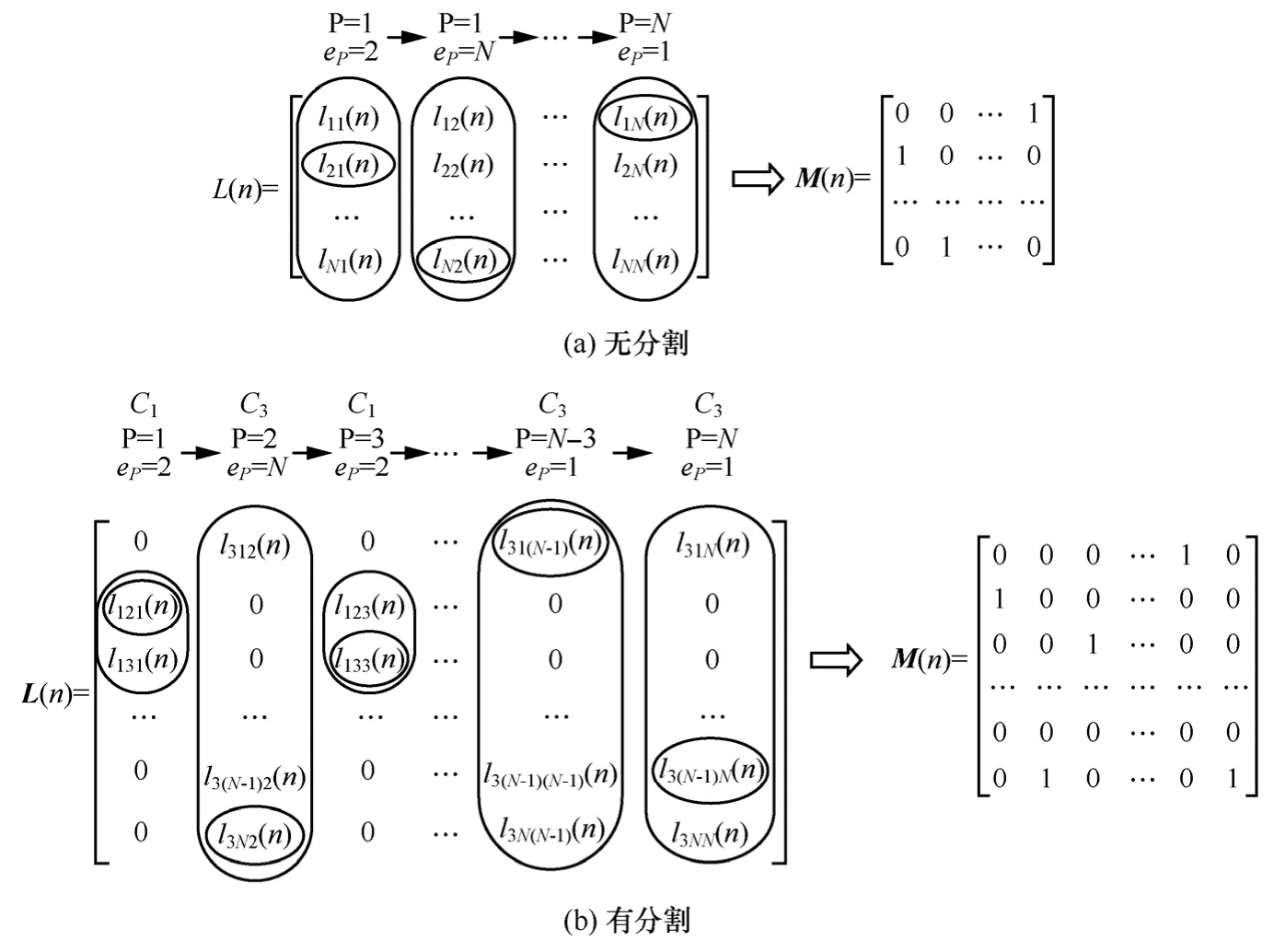
图5 步骤4中无分割仲裁和有分割仲裁的比较

步骤4 优先级指针P指向输出端口Op所对应的队长矩阵列向量(n)中同一SD中权重最大（队列最长）的元素eP，eP决定了M'(n)中第P列非0元素的位置。

步骤5 如果P=P+1modN≠1，重复步骤4；如果P=P+1modN=1，执行下一步。

步骤6 将{eP,P=1,2,…,N}送入M'(n)，n=n+1，转向步骤2。

步骤4中无分割仲裁和有分割仲裁的比较如图5所示，图5(b)中以3个SD为例表示，可见步骤4中，对于无分割交换结构，其单次进行N个权值的仲裁，分割交换结构单次进行Nk个权值的仲裁，减小了仲裁复杂度。

4 仿真实验

本文采用基于Crossbar交换性能仿真平台SPES(switching performance evaluation system)[21]设计并实现了基于交换结构分域的输入排队调度算法。

在原来仿真平台基础上，增加了网络承载控制系统，该系统配置或随机生成调度域分割参数，并将参数传递给输入端子系统、输出端子系统和调度子系统，以决定其调度过程所对应的SD和Crossbar匹配点，其仿真结构如图6所示。

1) 相对运算复杂度仿真

该仿真中假设平均分成3个SD，满足不同SD端口数之差不大于1。图7给出了传统矩阵模型的LQF与域调度的DSLQF算法的相对运算复杂度比较曲线图，相对运算复杂度是对调度算法中算术加法次数进行的相对比较结果。当交换结构端口数N依次从4增加到20时，相对运算复杂度曲线呈类指数迅速增加，传统的LQF算法的相对运算复杂度大于DSLQF算法的相对运算复杂度。

相对运算复杂度的减小主要由交换结构SD的个数决定，如果SD分割个数增加，则其运算效率还会提高，但倍数低于SD个数。对于同一个Crossbar交换结构，DSLQF算法的相对运算复杂度随SD个数增加而减小，但非线性关系。图8为16× 16 Crossbar结构相对运算复杂度与SD个数关系图，其SD对应端口数分割原则为：不同SD端口数之差不大于1。

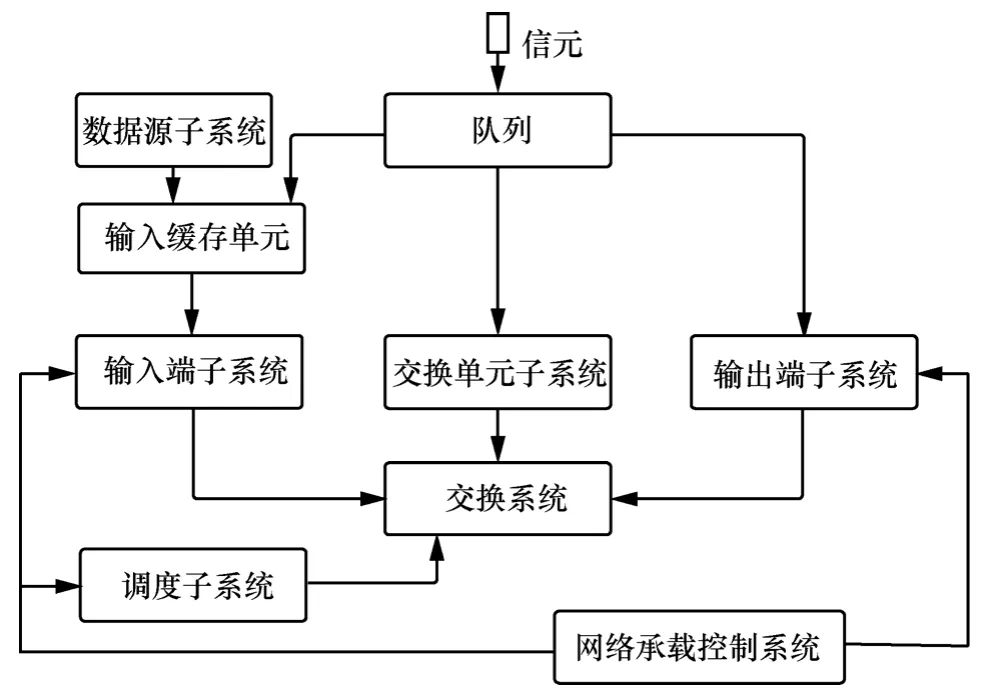
图6 加入分割参数的输入排队仿真平台

图7 SM-LQF与LQF相对运算复杂度比较

图8 相对运算复杂度与SD个数关系

2) 不同负载时延仿真

时延仿真采用16×16的交换结构，cell长度为64byte，仿真业务选取了贝努利业务源和ON-OFF突发业务源，其中突发业务的突发长度为20，目的端口分布分别采用均匀分布和 Diagonal分布，Diagonal分布的表达式为

图9(a)给出在贝努利均匀业务源条件下，各调度算法在归一化负载强度区间[0 .6,1]的平均时延对比曲线，用 T(*)表示*调度算法的时延。可见，输出排队 FQ的T(FQ)最小， T(SDRR-DSLQF)次之，输入排队LQF的T(LQF)最大，分层调度算法的时延均小于非分层调度。LQF、DRR-LQF、SDRR-LQF和SDRRDSLQF 4种调度算法的时延比较，T(LQF)＞ T(DRR-LQF)表明分层调度的时延特性优于非分层调度，因为分层调度将调度过程分为组内调度和组间调度 2个部分，将输入调度中整体集中式的复杂度变为局部调度复杂度之和，减小仲裁端口数，减小了算法复杂度。 T(DRR-LQF)＞T(SDRR-LQF)表明SDRR比DRR调度算法时延小，原因是SDRR的轮询过程采用份额借用机制，使得单个时隙内更多信元被调度。

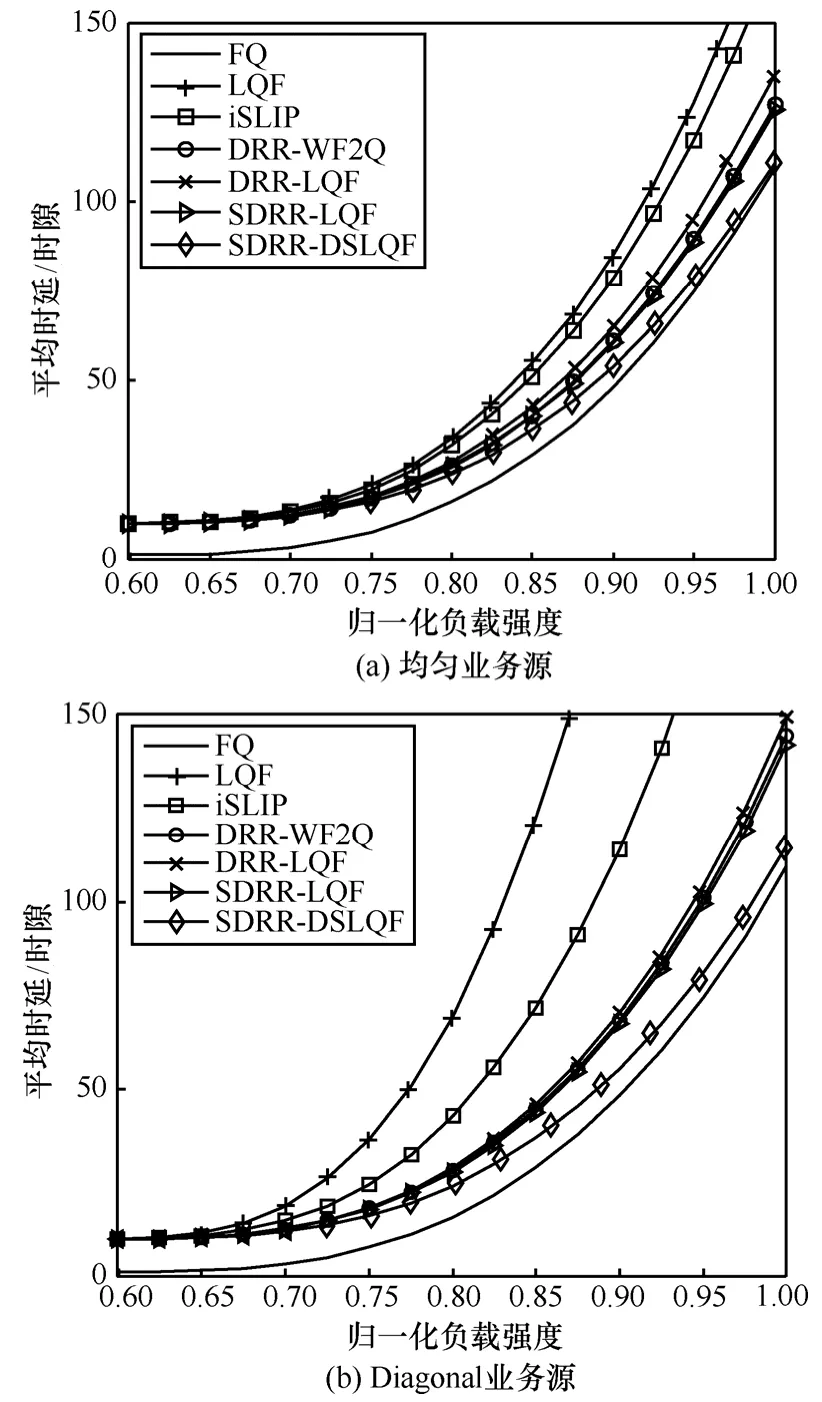
图9 贝努利业务源时延对比

T(SDRR-LQF)＞T(SDRR-DSLQF)表明分域的调度比不分域调度时延小，原因是分域调度仲裁复杂度小。

图 9(b)给出在贝努利 Diagonal业务源条件下，各调度算法在归一化负载强度区间[0.6,1]的平均时延对比曲线。与图 9(a)比较可见，非均匀业务源条件下的时延比均匀业务源条件下的时延大，非均匀业务源对输出排队FQ的T(FQ)影响最小，对输入排队LQF和iSLIP的时延影响最大，非均匀业务源输入与均匀业务源输入下的时延大小关系不变。

图 10(a)给出在 ON-OFF突发均匀业务源条件下，各调度算法在归一化负载强度区间[0 .6,1]的平均时延对比曲线。与图9(a)比较可见，ON-OFF突发业务源输入下的时延约为贝努利业务源输入下时延的10倍，ON-OFF突发业务源对各算法时延的影响相同，ON-OFF突发业务源输入与贝努利业务源输入下各算法时延大小关系不变。

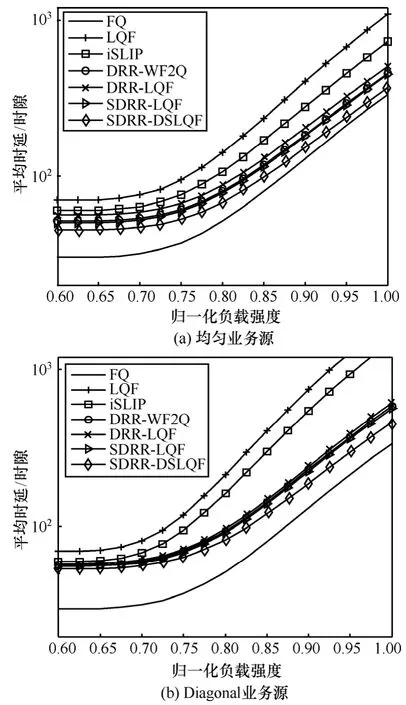
图10 ON-OFF突发业务源时延对比

图10(b)给出在ON-OFF突发Diagonal业务源条件下，各调度算法在归一化负载强度区间[ ]0.6,1的平均时延对比曲线。与图10(a)比较可见，非均匀突发业务源输入下的时延大于均匀突发业务源输入下的时延，在非均匀突发业务源条件下，输入排队LQF和iSLIP的时延增长迅速，非均匀突发业务源输入下的时延与均匀突发业务源输入下的时延大小关系不变。

对以上仿真结果分析得出如下结论：

1) 对于N×N的Crossbar交换结构，SD个数越大，相对运算复杂度越小，当个数为N时，每个SD只有一个端口，无需仲裁就可调度，可实现调度延迟为0。

2) 在 4种业务源输入条件下，ON-OFF突发Diagonal业务源输入下的时延最大。

3) 任何一种业务源输入下，输出排队FQ调度算法的时延都是最小，且在均匀和非均匀业务源条件下保持稳定，可见输出排队虽然需要内部加速，但能为业务提供好的时延QoS保证。

4) 任何一种业务源输入下，分层调度的时延总小于非分层调度的时延，主要原因是分层调度将调度过程分为组内调度和组间调度2个部分，将输入调度中整体集中式的复杂度变为局部调度复杂度之和，减小仲裁端口数，减小了算法复杂度。

当然从理论上分析，该算法也存在一些不足:

1) Crossbar交换结构分域承载组调度的前提是在可重构网络技术体系下构建 RSCN的需求，RSCN对输入输出端口的约束性条件形成了自封闭的调度域，域内包括几个 RSCN的业务，且每个RSCN业务不全部使用域内输入输出端口。如果没有这个前提，则该分域调度就会出现输入到输出交换路径的不可达问题。

2) 分域承载组调度中的域分割参数是由网络级可重构综合管理系统下达，当单个网络节点接收到该分割参数后，需要停机进行先分割再启动后调度的过程，增加了宕机时延。

3) 分域承载组调度算法的设计需具有可重构性，即需要根据分割参数进行调度的变化，当N很大时，重构过程需确定大量关闭的Crossbar交叉节点，会提高一定的复杂度。

5 结束语

在目前对通信节点功能和性能要求越来越高的发展模式下，可以通过构建RSCN实现网络级的优化，通过分割节点资源，尤其是节点内的交换资源，来满足不同RSCN业务的区分服务。交换结构的分割带来了调度算法的分割，业务特性需求（时延、抖动和分组丢失率等）的不同，对调度算法也有不同的要求，可采用单个调度域中部署不同调度算法来满足要求，这样就可以为特定的业务实现独立的调度，采用交换资源独享将QoS等级划分。

[1] 张伟, 吴春明, 姜明. 网络业务聚类研究[J]. 解放军信息工程大学学报, 2009, 10(1):53-56.ZHANG W, WU C M, JIANG M. Study of network services aggregation[J]. Journal of Information Engineering University, 2009, 10(1):53-56.

[2] 龚双瑾, 刘多, 张雪丽等.下一代网关键技术及发展[M]. 北京: 国防工业出版社, 2006.GONG S J, LIU D, ZHANG X L, et al. Key Technology and Development of Next Generation Network[M]. Beijing: National Defense Industry Press, 2006.

[3] CAPONE A, ELIAS J, MARTIGNON F. Routing and resource optimization in service overlay networks[J]. Elsevier Computer Networks,2009, 53(2):180-190.

[4] YU M, YI Y, REXFORD J. Rethinking virtual network embedding:substrate support for path splitting and migration[J]. ACM SIGCOMM Computer Communications Review, 2008, 38(2):17-29.

[5] ZHUGE B, YU C, LIU K P. Research on internal flow control mechanism of ForCES routers[J]. Information Technology Journal 2011 Asian Network for Scientific Information, 2011, 10(3):626-638.

[6] KESIDIS G, MCKEOWN N. Output-buffer ATM packet switching for integrated-services communicateon networks[A]. Proceedings of IEEE ICC’97[C]. Montreal, Canada, 1997. 342-350.

[7] MEKKITTIKUL A, MCKEOWN N. A practical scheduling algorithm for achieving 100% throughput in input-queued switches[A]. INFOCOM‘98[C]. San Francisco, CA, 1998. 792-799.

[8] MEKKITTIKUL A. Scheduling Non-uniform Traffic in High Speed Packet Switches and Routers[D]. Stanford University, 1998. 17-20.

[9] GIACCONE P, PRABHAKAR B, SHAH D. Towards simple highperformance schedulers for high-aggregate bandwidth switches[A].IEEE INFOCOM2002[C]. New York, USA, 2002. 120-127.

[10] LEE Y, LOU J Y, LUO J Z. An efficient packet scheduling algorithm with deadline guarantees for input-queued switches[J]. Journal IEEE/ACM Transitions on Networking, 2007, 15(1): 212-225.

[11] LEONARDI E, MELLIA M, NERI F. Design and implementation of a fast VOQ scheduler for a switch sabric[J]. IJCSNS International Journal of Computer Science and Network Security, 2008, 8(9):32-36.

[12] CAPRITA B, NIEH J, CHAN W C. Group round robin: improving the fairness and complexity of packet scheduling[A]. Proc of the ACM/IEEE ANCS[C]. Princeton, New Jersey, USA, 2005. 29-40.

[13] BENNETT J C R, ZHANG H. WF2Q: worst-case fair weighted fair queuing[A]. Proc of the IEEE INFOCOM[C]. New York, USA, 1996.120-128.

[14] SHREEDHAR M, VARGHESE G. Efficient fair queuing using deficit round robin[J]. IEEE/ACM Transactions on Networking, 1996, 4(3):375-385.

[15] PAREKH A K, GALLAGER R G. A generalized processor sharing approach to flow control in integrated services networks: the single-node case[J]. IEEE/ACM Transactions on Networking, 1993, 1(3):344-357.

[16] YUAN X, DUAN Z. FRR: a proportional and worst-case fair round robin scheduler[J]. IEEE Transactions on Computers, 2009, 58(3):365-379.

[17] COMER D, MARTYNOV M. Design and analysis of hybrid packet schedulers[A]. Proc of the IEEE INFOCOM 2008[C]. Phoenix, AZ,2008. 1570-1578.

[18] GUO C X. Improved smoothed round robin schedulers for high-speed packet networks[A]. Proc of the IEEE INFOCOM[C]. Phoenix, AZ,2008. 1579-1587.

[19] 张贤达. 矩阵分析与应用[M]. 北京: 清华大学出版社, 2004. 101-106.ZHANG X D. Matrix Analysis and Application[M]. Beijing: Tsinghua University Press, 2004. 101-106.

[20] 马祥杰, 毛军鹏, 兰巨龙. 输入排队Crossbar架构下的矩阵模型及MM-LQF调度策略[J]. 电子学报, 2008, 36(1):9-16.MA X J, MAO J P, LAN J L. Matrix model for input-queued crossbar fabric and MM-LQF scheduling scheme[J]. Journal of Electronics,2008, 36(1):9-16.

[21] HU H C, YI P, GUO Y F. Design and implementation of high performance simulation platform for switching and scheduling[J]. Journal of Software, 2008, 19(4):1036-1050.