Keccak类非线性变换的差分性质研究

李倩男，李云强，蒋淑静，路遥

(1. 信息工程大学 电子技术学院，河南 郑州 450004；2. 中国科学院 光电研究院，北京 100094；3. 国防科学技术大学 计算机学院，湖南 长沙 410073）

1 引言

2010年12月10日，美国国家标准与技术协会（NIST）公布进入 SHA3竞选算法[1～3]最后一轮的5个杂凑算法[4]，由Bertoni G、Daemen J和Peeters M等人设计的Keccak杂凑算法就是其中之一[5]。Keccak杂凑算法蕴涵着杂凑算法的最新设计理念[6,7]，对其编码环节的系统分析具有重要的理论和应用价值。χ变换是Keccak压缩函数中唯一的非线性环节，也是文献[8～10]的算法所选用的非线性环节，文献[11]中通过对Keccak的非线性环节进行改造，构造了新的非线性变换MiniKeccak。密码算法抵抗差分分析的强度也一直是人们关注的问题，对密码算法中的重要环节进行差分分析有助于分析整个密码算法的抗差分分析攻击的强度，也有助于对算法中的编码环节进行更深刻的认识和把握。为了更好地应用Keccack类非线性变换编码环节，本文将对其差分性质进行系统研究。

2 基本概念

则称Y=f( X)为n元Keccak类非线性变换。

显然，Keccak压缩函数中χ变换是5元Keccak类非线性变换，MiniKeccak中的非线性变换是3元Keccak类非线性变换。

定义2 设(X, +)，(Y, +)是有限交换群，f: X→Y，α∈X,β∈Y,

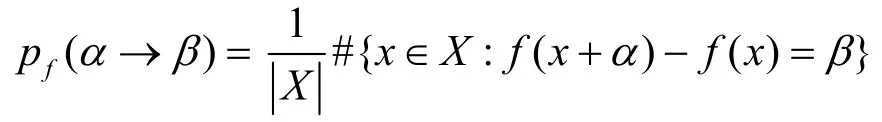
则称pf(α→β)为f在输入差为α条件下，输出差为β的差分转移概率，并称α→β为f的一个差分对应，称pf(α→β)为该差分对应的转移概率。其中，和#{·}均表示集合·中的元素个数。

定义3 设X=(x0, x1,…,xn-1)∈GFn(2)为n维布尔向量，称X=(x0, x1,…,xn-1)中的不为零的分量的个数为X的汉明重量，记做WH(X)。

3 差分性质分析

定理1 对于n元Keccak类非线性变换f，如果α, α′,β, β′∈，且β=f( x⊕α)⊕f( x)，＜α′, β′＞∈{＜a, b＞|a=(α＜＜j)且b=(β＜＜j ),0≤j＜n,j∈Z}， 那 么 差 分 转 移 概 率pf(α′→β′)=pf(α→β)。

证明 当j=1，即α′=(α＜＜1)时，输入、输入差和输出差从高位比特到低位比特依次可以表示为：x=(x0, x1,…,xn-1)，α=(α0,α1,…,αn-1)，β=(β0,β1,…,βn-1)，x′=(x0′, x1′,…,xn′-1)，α′=(α1,α2,…,αn-1,α0)， β′=(β0′,β1′,…,βn′-1)， 其 中 ，i∈{0,1,…,n-1}。那么输出差β和β'的每一个比特的差分变换布尔函数表达式可以写为

可知，当α′=(α＜＜1)，x′=(x＜＜1)时，有β′=(β＜＜1),f((x＜＜1)⊕(α＜＜1))⊕f((x＜＜1))=(β＜＜1)， 即f( x′⊕α′)⊕f( x′)=β′。 所 以 ，x′=(x＜＜1)∈。

pf(α′→ β′)==pf(α→β)，所以pf(α′→β′)=pf(α→β)。

假设j=m-1,(1＜m＜n, m∈Z)，pf(α′→β′)=pf(α→β)成立。j=m时的情况就是在j=m-1的基础上继续向左循环移动1位，由j=1时的结论，pf(α′→β′)=pf(α→β)也成立。所以，由数学归纳法可知定理1成立。

定理2 对于Keccak类非线性变换f，如果α, β, γ∈，pf(α→β)≠0，pf(α→γ)≠0，那么差分转移概率pf(α→β)=pf(α→γ)。

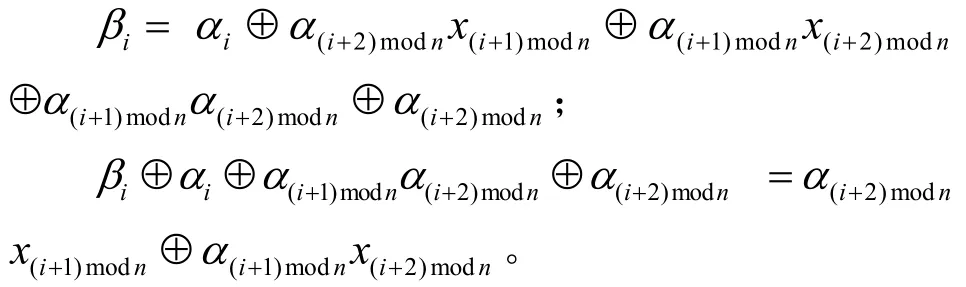
为系数矩阵，设系数矩阵A的秩R(A)=r，X

0

为一个特解，那么所有的解可以表示为

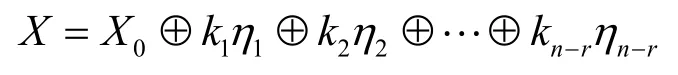
其中，kl∈{0,1}，l∈{1,2,…,n-r} ；，cm,n∈{0,1}，其中，m∈{1,2,…,n-r}，n∈{1,2,…,r} 。η1,η2,…,ηn-r为线性无关的基础解系。

由于kl∈{0,1}，l∈{1,2,…,n-r}，所以方程组解的个数为2n-r个，||=2n-r。

又pf(α→β)==pf(α→γ)，所以定理2成立。

定理3 对于n(n≥3)元Keccak类非线性变换f，如果输入差α，输出差β，使β=f( x⊕α)⊕f( x)成立，且pf(α→β)≠0和1，那么。

证明 按照定理2的证明方法，pf(α→β)≠0时，将输入、输入差和输出差从高位比特到低位比特依次可以表示为：x=(x0, x1,…,xn-1)，α=(α0,α1,…,αn-1)，β=(β0,β1,…,βn-1)，令yi=βi⊕αi⊕α(i+1)modnα(i+2)modn⊕α(i+2)modn， 其 中 ，xi,αi, βi,yi∈{0,1}，i∈{0,1,…,n -1}。={x| f( x ⊕α)⊕f( x)=β}，中元素个数||就是xi, yi∈{0,1}，i∈{0,1,…,n-1}的线性方程组解的个数。线性方程组的矩阵形式为

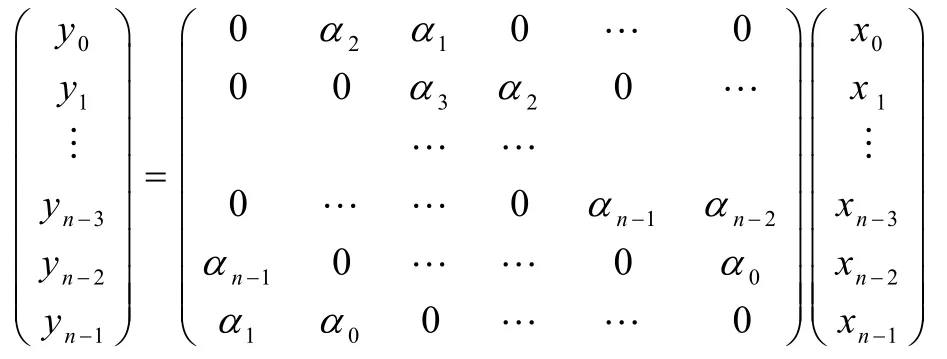
矩阵A的每一行和每一列都有输入差的2bit，且同1bit出现在矩阵不同的行和列中，所以矩阵A中非零的行数越少，r越小；当矩阵A的每一行都有非零的元素时，r为最大值。显然，当α=0，即A为零矩阵时，r=0；当α有1bit非零时，由于非零的比特出现在矩阵不同的行和列中，所以r=2；

当α有n-1和nbit非零时，矩阵A的所有行均非零。当α有n-1bit非零时，不妨设αi=0，

综上，定理3成立。

定理4 对于n元Keccak类非线性变换f，如果 ＜α, β＞∈{＜(a＜＜j),(b＜＜j)＞|a=，其中*表示这个比特可以任意取0或1，那么。

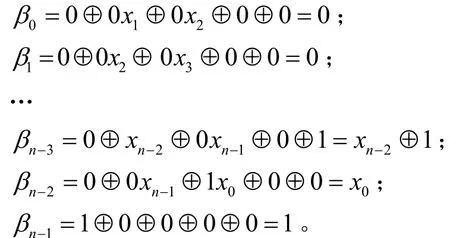
再由定理1，

综上，定理4成立。

定理5 对n元Keccak类非线性变换f，如果＜α, β＞∈{＜(a＜＜j),(b＜＜j)＞|a=或(·⊕1));或WH(a)=n,其中，*表示这个比特可以任意取0或1，·和(·⊕1)表示这2bit是互补的,0＜j≤n ,j∈Z}，则差分转移概率

3) 输入差α的汉明重量WH(α)=n,pf(α→β)≠0时，按照定理2的证明方法，将输入、输入差和输出差从高位比特到低位比特依次可以表示为：x=(x0, x1,…,xn-1)，α=(α0, α1,…,αn-1)，β=(β0, β1,…,βn-1)，令yi=βi⊕αi⊕α(i+1)modnα(i+2)modn⊕α(i+2)modn，其中，xi,αi, βi,yi∈{0,1}，i∈{0,1,…,n-1}。，则方程组解的个数即为WH(α)=n时，中元素的个数||。为系数矩阵，系数矩阵的秩R(A)=r=n-1；所以||=2n-(n-1)=2，。

当WH(α)=n时，β的每个比特的布尔函数表达式为：

βi=x(i+1)modn⊕x(i+2)modn⊕1，其中，xi∈{0,1}，i∈{0,1,…,n -1}。

当n为偶数时：

所以，此时输出差β的汉明重量为偶数。

同理可以证明，当WH(α)=n，n为奇数时，对于所有的WH(β)为奇数的输出差β，都有pf(α→β)=。

综上，定理5成立。

定理6 n元的Keccak类非线性变换f和n+1元的Keccak类非线性变换g有如下关系：对于n元Keccak类非线性变换f，输入差α=(0,0,α0,α1,…,αn-3)，输出差β=(β0,β1,…,βn-1)，对应的差分转移概率为pf(α→β)；n+1元Keccak类非线性变换g，输入差α′=(0,0,0,α0,α1,…,αn-3)，输出差 β'=(0,β0,β1,…,βn-1)，差分转移概率为pf(α′→β′)；那么pg(a′→β′)=pf(α→β)。其中,αi, βj∈{0,1},i∈{0,1,…,n-3},j∈{0,1,…,n -1}。

证明 当输入x=(x0, x1,…,xn-1)、α=(0,0,α0,α1,…,αn-3)时，n元Keccak类非线性变换f对应的输出差β每个比特的布尔函数表达式为：

当 输 入x′=(x0′,x1′,x2′,…,xn′ ),α=(0,0,0,α0,α1,…,αn-3)时，n+1元Keccak类非线性变换g对应的输出差β'每一个比特的布尔函数表达式为：

由 表 达 式 可 知 ， 当x0=x0′,xi=xi′+1(1≤i≤n-1)时，β=(β0,β1,…,βn-1)，β′=(0,β0,β1,…,βn-1)；x1′取值0或1对β′的值没有影响。记，那么

pg( a′ →β′)==pf(α→β)，所以，pg(a′→β′)=pf(α→β)。

综上，定理6成立。

4 结束语

杂凑函数Keccak中的压缩函数的非线性变换已经被广泛应用到很多密码算法中，文献[11]通过对其进行改造，提出了Minikeccak的非线性变换，并取得了良好的效果。为了更好地应用这一类非线性变换，本文建立了n元Keccak类非线性变换模型，并且分析了它的差分转移概率性质，给出了最大的非平凡差分转移概率和最小的非平凡差分转移概率的结构和计数，给出了这类非线性变换相邻变元间取相同差分转移概率的结构。但是，还有许多Keccak类非线性变换模型的差分性质例如次大差分转移概率、差分转移概率为0的结构等情况，本文还没有去研究分析。另外，对Keccak类非线性变换模型的Walsh谱值特性的研究将是下一个工作重点。

[1] NIST. Announcing request for candidate algorithm nominations for a new cryptographic hash algorithm (SHA-3) family[J]. Federal Register Notices 72, 2007, 212: 62212-62220.

[2] ANDREW R, RAY P, CHANG S J. Status Report on the First Round of the SHA-3 Cryptographic Hash Algorithm Competition[R]. Information Technology Laboratory National Institute of Standards and Technology, Gaithersburg, 2009.

[3] MELTEM S T, RAY P, LAWRENCE E B, et al. Status Report on the Second Round of the SHA-3 Cryptographic Hash Algorithm Competition. Computer Security Division[R]. Information Technology Labo-ratory National Institute of Standards-and Technology, Gaithersburg,2011.

[4] NIST. The SHA-3 Finalists candidates U S department of commerce national information service[EB/OL]. http://csrc. nist.gov. /groups/ST/hash/sha-3/Round3/submissions_round3. html.

[5] GUIDO B, JOAN D, MICHAEL P, et al. Keccak sponge function family main document[EB/OL]. http://csrc. nist.gov /groups/ ST /hash/sha-3 /Round1/submissions_round1. Html.

[6] 薛宇, 吴文玲, 王张宜. SHA3杂凑密码候选算法简评[J]. 中国科学院研究生院学报,2009, 26(5): 577-586.XUE Y,WU W L,WANG Z Y. Remarks of candidates hash algorithms for SHA3[J].Journal of CAS Postgraduates, 2009, 26(5): 577-586.

[7] 罗岚,叶娅兰,许春香等.在信念网模型下的 SHA3前五名算法注记[EB/OL].http://www.scienceet.cn/upload/blog/f-ile/2010/12/201012 1592436256375.pdf.LUO L, YE Y L, XU C X, et al. A note finalist5 of SHA3 at faithful network[EB/OL].http://www.scienceet.cn/upload/blog/file/2010/12/2010121592436256375.pdf.

[8] GUIDO B, JOAN D, MICHAEL P, et al. A belt-and-mill hash function[EB/OL]. http://radiogatun.noekeon.org.

[9] JOAN D, CLAPP C S K. Fast hashing and stream encryption with PANAMA[A]. Fast Software Encryption 1998 (S Vaudenay, ed)[C].1998. 60-74.

[10] JOAN D. Cipher and Hash Function Design Strategies Based on Linear and Differential Cryptanalysis[D]. Belgium: Katholieke Universities Leuven, 1995.

[11] EPHRAIM A. Sharing Nonlinear Gates in the Presence of Glitches[D].Enschede, Holland: University of Twente, 2010.