桩承式路堤土拱效应三维分析
2012-08-11王军军
费 康,王军军,陈 毅
(1.扬州大学 岩土工程研究所,江苏 扬州225127;2.河海大学 岩土力学与堤坝工程教育部重点实验室,南京210098)
桩承式路堤是指在地基中设置刚性桩或半刚性桩来支承路堤填土荷载,其具有施工速度快、沉降小、稳定性高等特点,近年来在工程中得到了广泛应用[1-2]。
在路堤荷载作用下,地基土的沉降大于桩的沉降,使得路堤填土中出现剪应力,荷载向桩顶转移,从而减小了作用在地基土表面的压力,这种现象称为“土拱效应”。桩承式路堤的设计思路在于经济合理的布置桩体,尽可能发挥路堤填土中的土拱效应,减少地基土承担的荷载。另一方面,如果在桩顶布置土工格栅等加筋材料,加筋材料的选择取决于其所承担的荷载。因而合理评价土拱效应对桩承式路堤的设计至关重要[3]。
Terzaghi[4]根据活板门试验研究了平面土拱效应,其假设填土中的破坏面为通过活动门边缘的竖直面,作用在地基土表面的荷载等于滑动体的重力减去边界上的摩阻力。Russell等[5]、Sloan等[6]将Terzaghi平面土拱效应理论推广到三维情况。Naughton[7]认为填土中的破坏面为通过桩边缘的对数螺旋曲线,该对数螺旋曲线的中心点为桩间土体的形心,作用在地基表面上的荷载为破坏面下方土体的重力,结果只适用于二维。Hewlett等[8](以下简称H-R方法)根据二维和三维的室内模型试验,假设填土中存在支撑于桩顶的圆形土拱,以拱顶或拱脚土体单元的极限平衡条件为设计控制状态。Zeaske等[9]根据模型槽试验和数值分析,假设三维土拱为多个壳单元组成的系统,即所谓的“多拱模型”。
由于采用了不同的路堤填土破坏模式,各方法之间的计算结果差异较大,与实测数据也有所区别[10-11]。笔者首先根据模型槽试验和有限元数值分析对桩承式路堤填土中的三维破坏模式进行分析,确定破坏面形状;然后进行理论推导,得到三维土拱效应的简化计算方法;最后与有限元计算结果和实测数据进行对比。
1 破坏模式的模型槽试验研究
1.1 试验概况
1.1.1 试验材料 试验在一长100cm、宽100cm、高150cm的钢制模型槽中进行。为方便观测,模型槽一侧为钢化玻璃。试验用桩采用C20混凝土,截面为正方形,边长a=10cm,桩长L=40cm,桩中心间距s=50cm,为方便观察桩顶土体变形,试验为“半模试验”,共使用了2根整桩和4根半桩,并将半桩与玻璃紧密贴合,具体布置方式见图1。
为了使得桩和地基土之间产生足够大的差异变形,充分发挥土拱效应,试验中地基土采用泡沫模拟,厚度t=40cm。根据室内侧限压缩试验结果,在15%的应变范围内,泡沫应力 应变近似为线性关系,压缩模量为28.2kPa。
路堤填土采用标准石英砂模拟,砂土的比重ds为2.65,不均匀系数Cu为3.22,曲率系数Cc为1.17。填筑时的控制干密度ρd=1.5g/cm3,相应密实度下由直剪试验确定的摩擦角为27.3°。为减少模型槽侧壁摩擦的影响,在砂土与玻璃壁之间涂抹凡士林,另外3边铺设塑料薄膜。由于桩的模量远大于地基土,桩的变形很小,模型槽侧壁摩擦对桩的性状影响较小,因此试验中未做额外的处理。
1.1.2 试验方法及仪器布置 试验中先将模拟软土地基的泡沫就位,再将桩插入到预留的桩孔中,随后进行砂土的填筑。填筑过程中以5cm为1层,分层填筑。每层填土之间铺设薄层彩砂,并在玻璃外侧绘制直线,通过比较变形前后的照片,可以直观的观察路段填土在不同填土高度下的变形模式。
为了评价填土中的土拱效应,试验中在2根桩的桩顶各布置了一个土压力盒(T1和T2),从桩间土的中心点往上以100mm为间距共布置了10个土压力盒(T3到T12),仪器具体布置见图1。
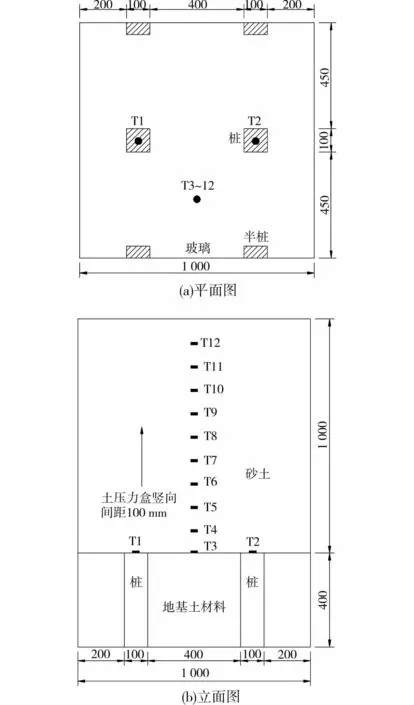
图1 试验模型的平面及立面图
1.2 试验结果分析
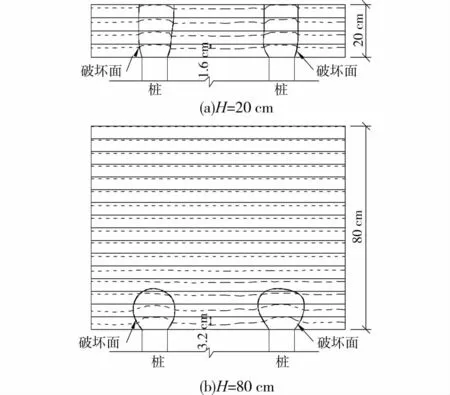
图2 观察到的破坏面
1.2.2 填土中的竖向应力分布 图3给出了实测的竖向应力分布。图中的深度是由填土表面向下起算的距离。结果表明,当填土高度较低时,竖向应力沿深度单一增加。当填土高度较高时,竖向应力分布曲线从上到下大致可以分为沿深度增加、减小、再增加3个阶段。
竖向应力沿深度的分布实质上是破坏模式的体现,图4将填土高度1.0m时的竖向应力分布理论值与实测值进行了比较。若认为破坏模式符合Terzaghi方法,在不考虑等沉面的情况下,计算得到的竖向应力应沿深度逐渐减小,且减小的速率越来越小,这与填土高度较小时的竖向应力分布特点相近。当填土高度较高时,考虑到桩顶某一高度以上的填土中沉降基本相等,该高度以上的填土中没有剪应力,Terzaghi方法中将其作为超载考虑。这种情况下计算得到的竖向应力分布曲线大致可分为2段,在等沉面高度以上为自重应力分布,以下则随深度逐渐减小。由此可见,无论是否考虑等沉面,Terzaghi方法的计算结果与试验实测曲线的分布形态都有所区别。
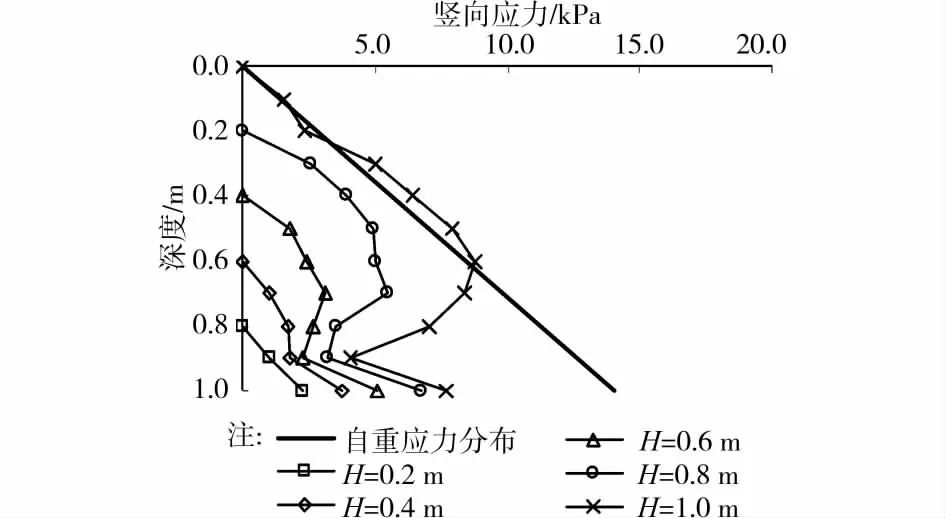
图3 不同填土高度时的竖向应力分布
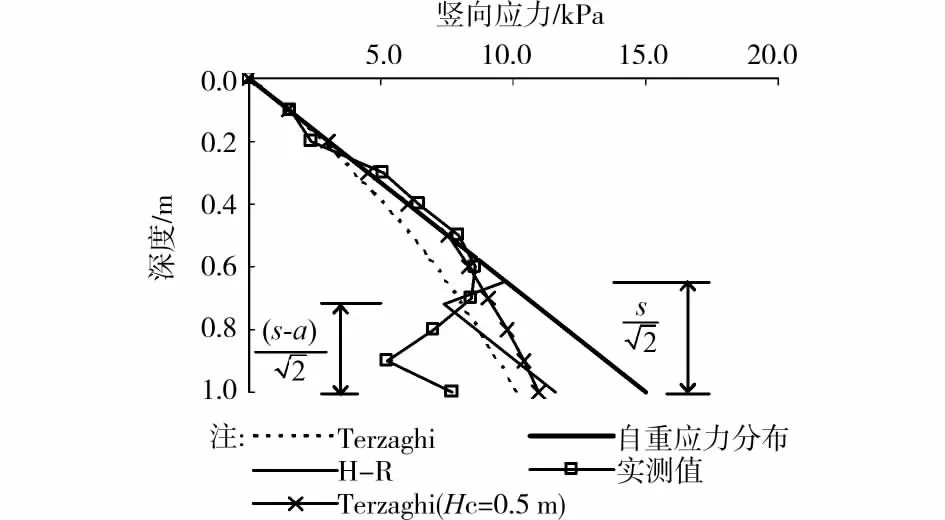
图4 竖向应力分布的理论计算值与实测值比较(H=1.0m)
根据H-R方法,填土中应存在球形土穹,对正方形布置的方桩土穹的内半径为外半径为在土穹顶部外侧以上的填土中竖向应力为自重应力线性分布;在土穹中,竖向应力减小;在土穹以下,竖向应力又开始增加。按照H-R的土拱效应理论,出现第2段曲线中的竖向应力的减小是因为填土中出现了土穹,竖向应力减小段的始点对应于土穹的外顶点,终点对应于土穹的内顶点。从试验结果来看,反算的土穹内顶点的位置比H-R方法明显的要低,H-R方法也存在一定的误差。
值得注意的是,如果在Terzaghi方法中考虑图2(b)所示的曲线滑动面,即考虑滑动体的宽度随高程变化,得到的竖向应力分布形态能较好的模拟实测规律(图5),这表明将破坏面看做局限在桩顶的泡状曲面是合理的。
另外注意到,填土高度1.0m时实测地基顶面竖向应力为7.4kPa,约为填土自重应力的0.49。此时桩顶应力实测值为178.8kPa(T1)和145.9kPa(T2),若将桩顶应力取为T1和T2的平均值162.3 kPa,则桩和土共同承担的荷载为13.6kN,与填土总荷载理论值15.0kN相差约9%,验证了实测数据的可靠性。
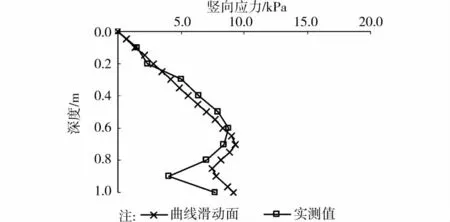
图5 Terzaghi折线滑动面法模拟的竖向应力分布
2 破坏模式的数值研究
2.1 有限元分析模型
2.1.1 几何模型及边界条件 计算中取一根桩及其控制范围进行分析。考虑到对称性,所采用分析模型的平面示意图如图6所示,图中的OAB为1/4桩,ACDEB为桩间地基土的表面。
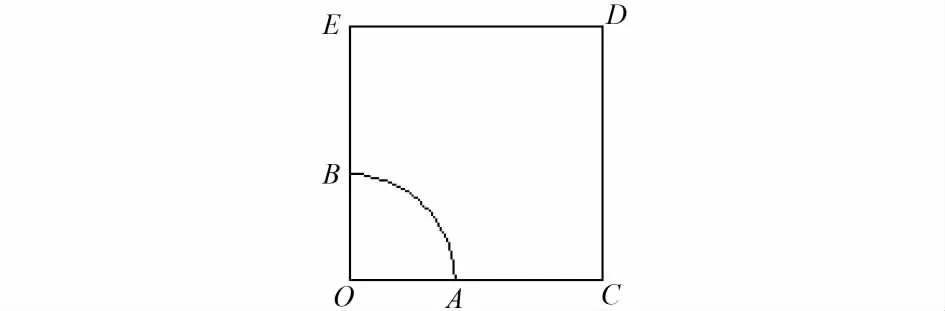
图6 有限元分析模型示意图
由于计算的重点是分析极限情况下的土拱效应,模型中可不包含桩体和地基土,差异沉降通过设置特定的边界条件来实现。具体做法为:约束桩顶和桩间填土顶面3个方向的位移,约束分析模型四周的水平位移,对填土按自重应力分布设置初始应力状态,即
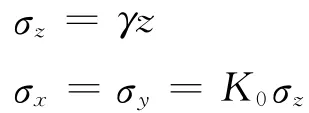
式中:σz是竖向应力;σx和σy是2个水平的应力;γ是填土的重度;K0=1-sinφ′是静止土压力系数;φ′是土体的有效摩擦角;z是从填土顶面起算的深度。
设置初始应力状态之后,在后续分析步中放松面ACDEB的位移约束条件,直至破坏。这种做法相当于在不排水条件下进行路堤填筑,随后地基土固结沉降,填土中出现了足够大的差异变形,直至土拱效应完全发挥,模拟的是极限情况。
2.1.2 材料模型及计算方案 路堤填土采用莫尔库仑理想弹塑性模型模拟,重度γ=20kN/m3,弹性模量E=20MPa,泊松比v=0.3。为便于与简化分析方法比较,取粘聚力c′=0kPa,摩擦角φ′分别取20°、25°、30°、35°和40°,不考虑材料的剪胀角。计算中桩径d=0.5m,桩间距s分别取1.0、1.5、2.0和2.5m,对每一个桩间距,填土高度H分别取1.0、2.0、3.0、4.0、5.0和6.0m。
2.2 填土中的破坏面分析
填土中的破坏面通过等效塑性应变增量的分布来反映,等效塑性应变εeq定义为:

式中εp是塑性应变张量。
图7给出了φ′=30°、s=2.5m时不同填土高度下的破坏面位置。清晰起见,图中只给出对角线剖面(图6中的OD)桩顶以上一倍桩净间距内的结果。结果表明,填土高度与桩间距之比时,破坏面与Terzaghi方法中假设的竖直面基本相似,其破坏面近似沿着桩边缘竖直面分布。而在的情况下,破坏面为桩顶的泡状曲面。
从破坏面形态来看,填土高度越大,泡状破坏面越扁,水平范围也越大。其它桩间距的计算结果也表现出相似的特性时为过渡状态。
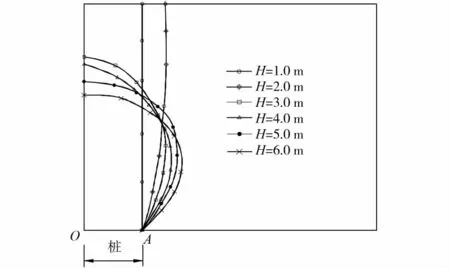
图7 破坏面的位置(φ′=30°)
不同摩擦角下的计算结果也表现出相同的规律,以s=2.5m,H=6.0m为例(图8),不同摩擦角下的破坏面都显示出相同的特性,即破坏面局限在桩顶上部填土内,且可近似看成对数螺旋面;摩擦角越大,破坏面范围也越大。
3 三维土拱效应简化分析方法
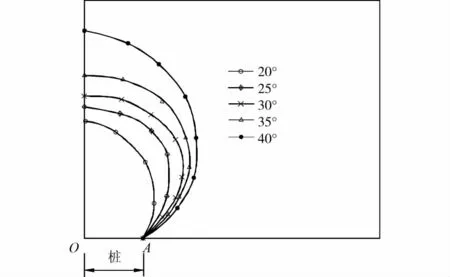
图8 不同摩擦角时破坏面的位置(s=2.5m,H =6.0m)
根据模型试验及有限元分析结果,桩承式路堤中填土的破坏模式可分为低路堤和高路堤破坏模式2种,当路堤填土较小时(),填土中的破坏面为通过桩边缘的竖直面,可仍采用Terzaghi土拱效应理论分析分析。当路堤填土较高时≥1.5),填土中的破坏面局限在桩顶局部范围内,可近似看成对数螺旋曲面,本章对高路堤破坏模式进行推导,进而得到相应的土拱效应分析方法。
3.1 破坏面形状
建立如图9所示的轴对称坐标系,原点O为桩中心点,r轴水平向右,z轴竖直向上。OA为桩的半径。假设破坏面ABCD是以O′为中心的对数螺
旋曲面,BE为通过O′点的竖直线,对数螺旋曲线上任一点D的切线方向与水平方向的夹角为δ,D点距O′点的距离R为R1exp[(ω-α1)tanφ],R1是O′C的长度,α1、α2、α3和ω意义如图所示。O′C的长度为R2=R1exp[(α2+α3)tanφ]。

图9 破坏面形状
3.2 方程推导
当O′点确定之后,D点的水平坐标为

α3由下式确定:
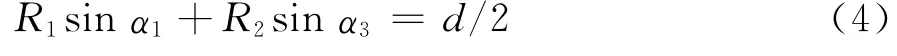
注意到R2与α3有关,α3可正可负。上式需迭代求解。进而可求得破坏区域的高度Hf。
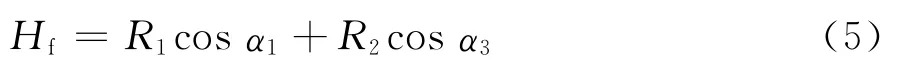
极限情况下,桩顶承受的荷载Pp包括2部分,即破坏面包含的土体自重W、破坏面边界上正应力σ和剪应力τ的合力在竖直方向的分量F。对于自重W有:
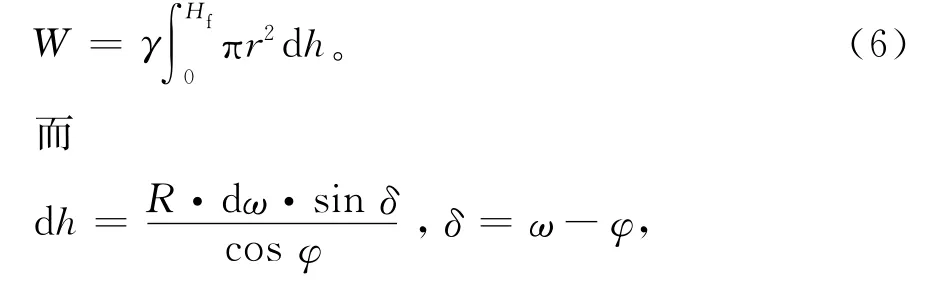
因而有
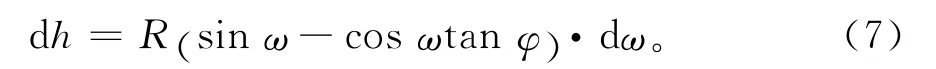
将式(4)和(8)代入式(7),考虑到
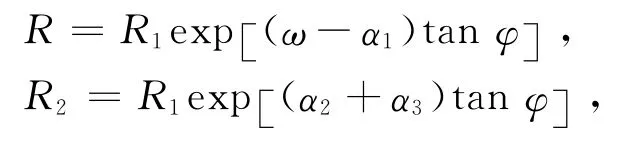
则有
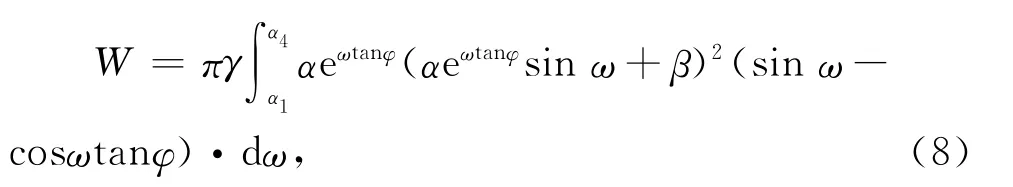
式中:α4=α1+α2+α3;α=R1/eα1tanφ;β=R2sinα3。
该积分可通过数值方法求得。
对于F,在活动面上取微分面积Rsecφdω·rdθ,θ是绕z轴旋转的角度,则该微分面积上应力沿竖向的分量为

考虑到破坏面上达到极限应力状态,即τ=σtanφ代入上式有
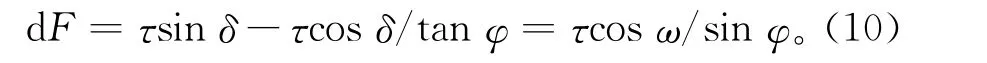
根据Kotter’s方程,破坏面上有
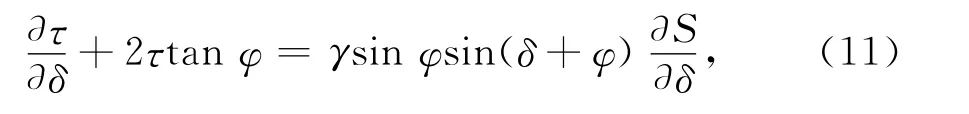
式中∂S是微分弧长。
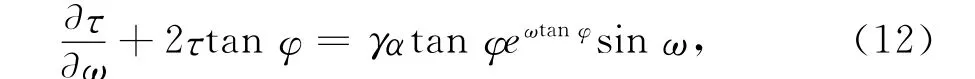
其解答为
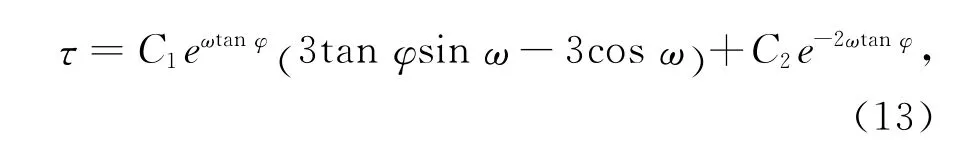
设在桩边缘处土体的竖向应力为σs,土拱效应完全发挥时其为小主应力,竖向应力为Kpσs,Kp是土的被动土压力系数,因而可得到破坏面上的剪应力τ*=(1 +Kp)σs×sinφ×cosφ,将其代入式(13)可 得C2=e2α1tanφ[τ*-C1eα1tanφ(3tanφsinα1-3cosα1)],因而可根据下式求得合力F,
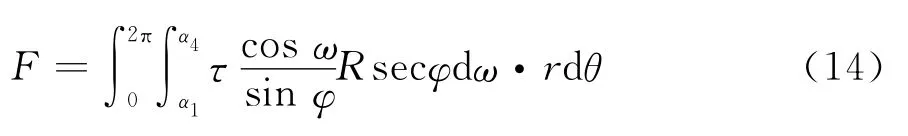
因而桩顶极限情况下承受的荷载为

3.3 求解方法
注意到在求解F时用到了桩间土表面的竖向荷载σs,其暂时未知,但与Pp应满足平衡关系,需迭代求解。具体求解步骤如下:
1)假设破坏面中心点位置,即R1和α1。
2)假设未发生土拱效应,即桩间土承受的荷载为σs填土荷载γH。
3)根据式(15)求解桩顶荷载Pp。
4)验算平衡条件是否满足,即σs×As+Pp=γHS2,式中As是桩间土的表面面积。如果平衡条件不满足,由计算σs后跳转到第3步。
5)平衡条件满足后计算应力折减系数

应力折减系数Sr在0~1之间,若Sr=1,意味着作用在桩间土表面的荷载就等于填土荷载,没有出现土拱效应。反之,若Sr=0,所有的荷载都转移到桩顶。
6)重复以上步骤,搜索确定最危险情况及最大的应力折减系数Sr。
4 简化分析方法的验证
4.1 与有限元计算结果的比较
图10(a)给出了应力折减系数Sr与填土高度和桩净间距之比的变化关系,图中的反映了不同桩间距的影响。由图可见,虽然简化分析方法计算得到的应力折减系数略高于有限元计算结果,但整体变化规律是一致的。随着增加Sr减小,但降低的速率逐渐放缓,填土高度较高后基本保持不变。而对不同m值,m值越小,Sr越大,地基土需要承担更多的荷载,因而需要合理的设置桩间距及桩帽尺寸。同时也注意到,当时,m对S的影响不明r显,这是因为此时路堤填土中的破坏模式主要是低填土路堤模式,土拱效应的程度只取决于破坏面上发挥的摩擦力,S主要与有关。
图10(b)给出了s=2.5m,H=6m时应力折减系数Sr与摩擦角φ之间的关系。结果表明,有限元方法和该简化方法得到的规律是一致的。随着摩擦角的增加,Sr减小的很明显,当φ=20°时,简化分析方法计算得到Sr=0.84;当φ=40°,Sr快速降低为0.25,更多的荷载通过土拱效应传递给桩。
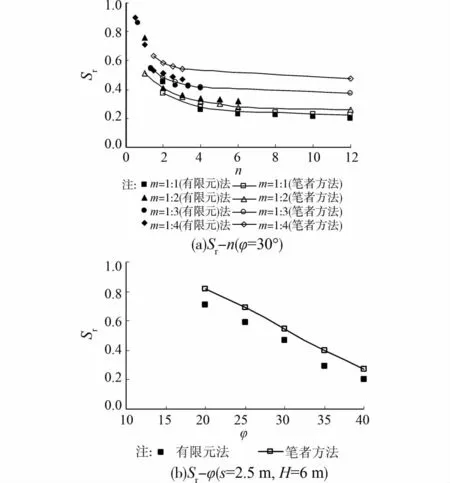
图10 应力折减系数的有限元和简化方法计算结果的比较
4.2 与试验结果的比较
将该方法计算得到的应力折减系数Sr与文献中收集的试验结果进行了比较。对比起见,表1中同时给出了该方法、H-R方法和Terzaghi方法的计算结果。需要指出,在应用Terzaghi方法进行计算时,存在2个不确定的因素,即竖直滑动面上的土压力系数K及等沉面高度Hc的确定。计算中,按Russell和Pierpoint[5]的建议将K取为1.0,Hc取为1.4(s-d)。在应用该方法时,需将方桩按照面积相等的原则转换为圆桩,即d=1.13a。
计算结果表明,H-R方法低估了土拱效应的程度,计算得到的应力折减系数偏大,桩净间距较大时偏差更为明显。对于Terzaghi方法,计算结果的精确度取决于等沉面高度和破坏面上的土压力系数的取值,这2点仍然存在不确定因素。整体上来看,对的路堤,由于采用了更合适的破坏模式,笔者提出的简化分析方法计算结果最好。如对试验1,实测的应力折减系数为0.49,该方法计算值为0.55,在所有方法的计算结果中最为接近。若考虑桩顶荷载,试验1中的桩顶应力实测值(T1和T2的平均值)为162.3kPa,对应的极限荷载为1.623 kN,与由该方法式(15)计算得到的1.792kN相差约9.4%,吻合度也较好。这是因为应力折减系数Sr反映的是桩间土体分担荷载的情况,Sr相同意味着土体承担的荷载相同,也就意味着桩承担的荷载也相同。
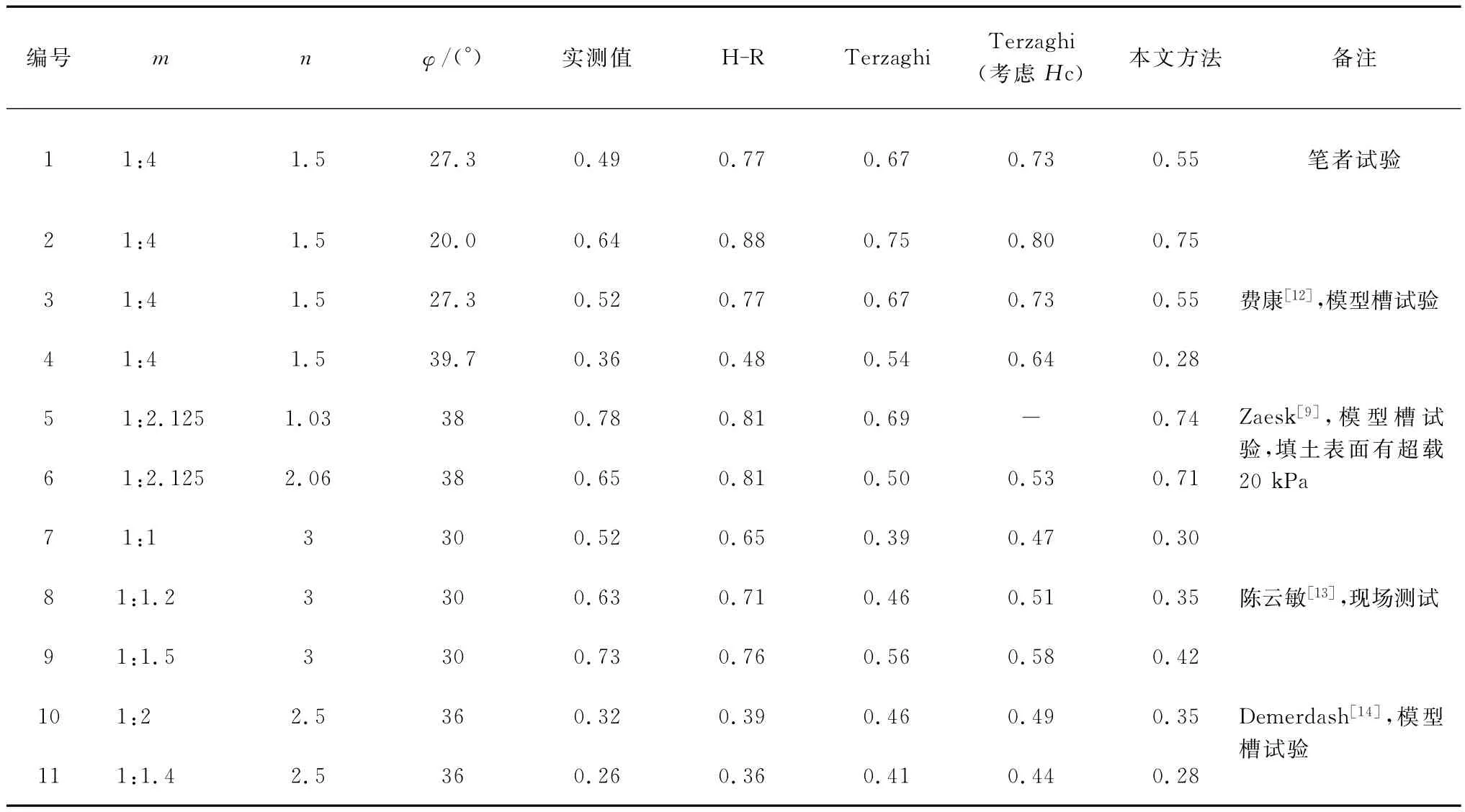
表1 应力折减系数的计算值与试验结果的对比
另外,也需要指出,该方法求解的是极限情况下的土拱效应。因而对试验7~9,该方法的计算结果明显偏小。这是因为试验7~9是现场测试数据,地基土有一定的支撑作用,桩和桩间土的差异沉降未能使得土拱效应完全发生。而试验1、试验2~4中地基土采用泡沫模拟,试验5~6地基土采用软弱粘土,试验10~11中采用了类似活动门试验的做法,地基土表面可任意沉降。在这些试验中桩和桩间土之间都产生了足够的差异沉降,填土达到了极限情况。
5 结 论
1)三维试验和有限元分析结果表明,桩承式路堤的破坏模式取决于路堤填土的高度,填土高度小于桩净间距时,破坏面从桩边缘向上竖直延伸至填土表面;随着填土高度的增加,破坏面逐渐演变为局限在桩顶的泡状曲面。
2)根据试验和有限元分析结果所假设的高路堤破坏模式,建立了土拱效应三维分析方法,并与有限元数值分析和试验结果进行了对比,结果吻合较好,验证了破坏模式和分析方法的可靠性。
3)所提出的三维简化分析方法适用于求解土拱效应完全发挥时的应力折减系数,未达到极限状态时桩、土之间的荷载分担需进一步研究。
[1]费康,刘汉龙.桩承式加筋路堤设计理论研究进展[J].水利水电科技进展,2008,28(4):89-94.FEI Kang,LIU Hanlong.Advances in research on design theory of geosynthetic reinforced pile supported embankment[J].Advances in Science and Technology of Water Resources,2008,28(4):89-94.
[2]费康,刘汉龙,高玉峰.路堤下现浇薄壁管桩复合地基工作特性分析[J].岩土力学,2004,25(9):1390-1396.FEI Kang,LIU Hanlong,GAO Yufeng.Performance of cast-in-situ concrete thin-wall pipe pile composite foundation under road embankment[J].Rock and Soil Mechanics,2004,25(9):1390-1396.
[3]Potts V J,Zdravkovic L.Finite-element study of arching behavior in reinforced soils [J].Ground Improvement,2010,163(4):217-229.
[4]Terzaghi K.Theoretical soil mechanics [M].New York:Wiley,1943.
[5]Russell D,Pierpoint N.An assessment of design methods for piled embankments[J].Ground Engineering,1997,30(11):39-44.
[6]Sloan J A,Filz G M,Collin J G.A generalized formulation of the Adapted Terzaghi Method of arching in column-supported embankments [C]//Proc.of GeoFrontiers,GSP 211Advanced in Geotechnical Engineering,Dallas,Texas,USA,2011:798-805.
[7]Naughton P J.The significance of critical height in the design of piled embankments[C]//Proc.GeoDenver,GSP 172Soil Improvement,Denver Colorado,USA,2007:13-23.
[8]Hewlett J, Randolph M F.Analysis of piled embankments[J].Ground Engineering,1988,21(3):12-18.
[9]Zaeske D,Kempfert H G.Berechnung und wirkungsweise von unbewehrten und bewehrten mineralischen Tragschichten über punktund linienförmigen Traggliedern [J].Bauingenieur,2002(77):80-86.Zaeske D,Kempfert H G.Calculation and mode of unreinforced and reinforced base layers on point and line shaped support members[J].Civil Engineering,2002(77):80-86.
[10]费康,刘汉龙.桩承式加筋路堤的现场试验及数值分析[J].岩土力学,2009,30(4):1004-1012.FEI kang,LIU Hanlong.Field test study and numerical analysis of a geogrid-reinforced and pilesupported embankment[J].Rock and Soil Mechanics,2009,30(4):1004-1012.
[11]Ellis E,Aslam R.Arching in piled embankments:comparison of centrifuge tests and predictive methods[J].Ground Engineering,2009,42(6):34-38.
[12]费康,王军军,陈毅.桩承式路堤土拱效应的试验和数值研究[J].岩土力学,2011,32(7):1975-1983.FEI kang,WANG Junjun,CHEN Yi.Experimental and numerical studies of soil arching in piled embankment[J].Rock and Soil Mechanics,2011,32(7):1975-1983.
[13]陈云敏,贾宁,陈仁朋.桩承式路堤土拱效应分析[J].中国公路学报,2004,17(4):1-6.CHEN Yunmin,JIA Ning,CHEN Renpeng.Soil arch analysis of pile-supported embankments [J].China Journal of Highway and Transport,2004,17(4):1-6.
[14]Demerdash M A.An experimental study of piled embankments incorporating geosynthetic basal reinforcement[D].Newcastle upon Tyne:Newcastle University,1996.
