滑坡概率分析中降雨的联合概率结构

范文亮，陈朝晖，李正良，余德祥，王 清

（1.重庆大学a.土木工程学院；b.山地城镇建设与新技术教育部重点实验室，重庆400045；2.重庆市沙坪坝区气象局，重庆400030）

滑坡是常见的地质灾害，其形成除与边坡自身的岩土特性有关外，尚取决于许多外部触发因素，如地震、降雨和边坡的不合理开挖等。其中，由降雨触发的滑坡（即降雨型滑坡）在世界上分布最广，发生频率最高，给人类造成的危害最大［1］。因此，降雨型滑坡的预测是防灾减灾工程的主要内容之一。

降雨型滑坡预测方法主要分为2类：基于过程的预测模型（亦称为物理模型）和经验模型。雨水渗入导致岩土体内的孔隙压力增大、有效应力减小和岩土体的抗剪强度降低是降雨型滑坡发生的主要机制［1］。滑坡预测的物理模型则从上述机制出发判断滑坡的状态，即充分考虑降雨数据、降雨入渗过程及其对岩土体的影响，结合岩土体滑坡的稳定性分析，最终确定引发滑坡的降雨量，从而判定滑坡是否发生［2－9］。然而，该模型所需输入信息，如局部地形条件、岩土的力学参数和水文学参数等都很难准确获得，阻碍了该模型的实际应用［10］。经验模型则部分体现了滑坡产生的机制，仅通过对降雨和滑坡的历史数据进行统计给出滑坡的降雨阈值。模型不同，降雨阈值所采用的控制变量亦不相同，所适用的地区亦不相同。但由于简便易行，经验模型是目前滑坡预测中最为实用的方法。

本质上，无论是物理模型还是经验模型，均是通过将降雨数据和滑坡的降雨阈值进行对比来判定滑坡的发生与否，只不过前者的降雨阈值是基于物理机制分析得到的，而后者则是通过经验统计给出的。借鉴可靠度理论的概念，滑坡概率Pf可表示为

式中：Pr｛·｝表示事件发生的概率；R表示当前降雨数据，类似于可靠度分析中的效应；［R］表示降雨阈值，类似于可靠度分析中的抗力。然而，由于降雨型滑坡影响因素的复杂性，很难由单一控制变量判定，因此R和［R］均为向量，而在可靠度分析中，效应和抗力均为标量。

目前，关于降雨型滑坡的研究主要集中于降雨与滑坡的关系、降雨的入渗和边坡的稳定性分析方面［11－16］，即更多地关注［R］，对于降雨数据R的概率描述鲜有研究涉及。笔者力图针对重庆地区的历年降雨数据，建立可用于重庆地区滑坡概率预测的降雨特征的概率模型。

欲建立R的概率模型，必须先将其具体化，明确其分量。文献［10］详细列举了各研究者曾经使用过的控制变量，包括日降雨量、前期累计降雨量、降雨强度和降雨持时等共25种。结合文献［13］和［17］，笔者取日降雨量和前期累计降雨量为控制变量，且取10d为前期降雨的计算时间段。

1 滑坡概率分析

若记日降雨量为R1，10d累计降雨量为R10，与之对应的阈值分别为 ［R1］、［R10］，那么式（1）可改写为式（2）。

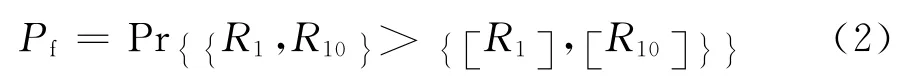
值得指出的是，现有研究中关于R1、R10的处理方式是截然不同的。日降雨量往往用降雨等级表示，即将R1视为离散变量，而10d累计降雨量则采用真实的数据，即R10视为离散变量，然后根据日降雨量的不同等级再结合10d累计降雨量的具体数值判定滑坡状态。

一般而言，根据日降雨量大小可分为4个等级，即等级1（小雨，R1∈［0，10）mm）、等级2（中雨，R1∈［10，25）mm）、等级3（大雨，R1∈［25，50）mm）和等级4（暴雨，R1∈［50，∞）mm）。若记第i个降雨等级为Ei，那么式（2）可进一步改写为

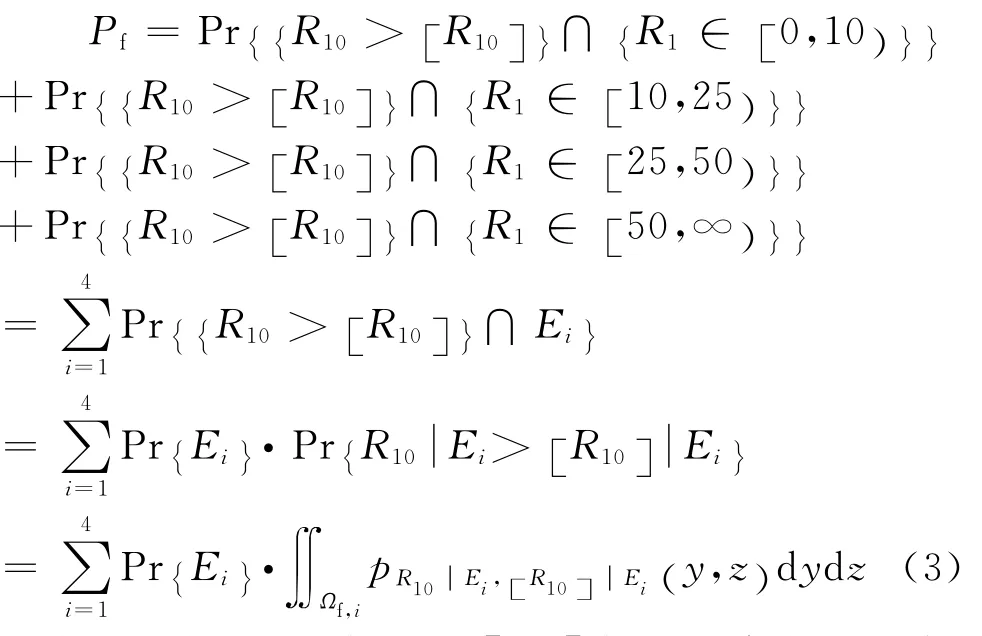
式中：Ωf，i表示R10｜Ei＞ ［R10］｜Ei所代表的区域；p（·）表示概率密度函数；Pr｛Ei｝为降雨等级的频度函数。

欲获取R10｜Ei和［R10］｜Ei的联合概率密度函数非常困难。考虑到［R10］｜Ei的影响因素除降雨外，尚包含局部地形参数、岩土力学参数等，而且降雨对［R10］｜Ei的影响通过Ei亦剥离了一部分，因此，为简便实用，通常可假定R10｜Ei和［R10］｜Ei相互独立，于是式（3）可简化为式（4）。

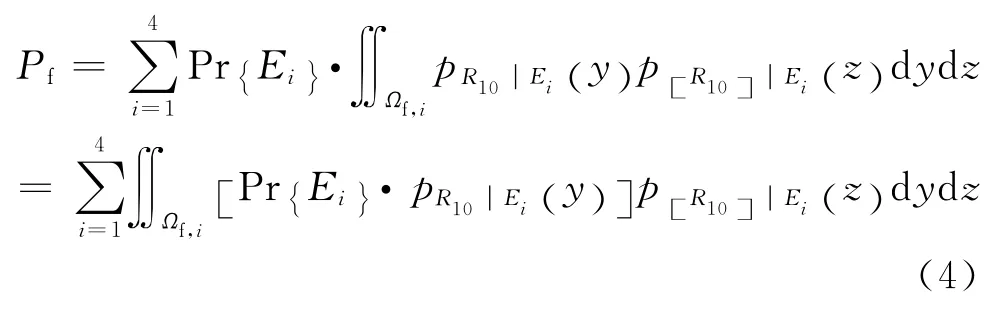
若已知 Pr｛Ei｝·pR10｜Ei（y）和p［R10］｜Ei（z），则滑坡概率计算颇为简单。本文则着重于关注Pr｛Ei｝·pR10｜Ei（y）的获取。由于Pr｛Ei｝·pR10｜Ei（y）描述了2个变量的联合概率结构，但是此2变量分别为离散变量和连续变量，因此，文中将称之为离散 连续混合变量的联合概率结构。

2 离散 连续混合变量的联合概率模型

由上所述，Pr｛Ei｝表示事件Ei发生的概率，pR10｜Ei（y）则表示随机变量的条件概率密度，本质上仍属于概率密度函数。根据降雨历史数据可以方便地给出Pr｛Ei｝的统计值，但是欲较为准确地确定pR10｜Ei（y）的模型则较为困难。目前应用最为广泛的由采样数据确定随机变量概率模型的方法是假设检验方法。该方法的优点在于可以给出一个简单的可用概率模型，但其确定亦是显而易见的，即只能确定单峰的概率密度模型。然而，由于影响因素的复杂性，现实中的许多随机变量并不能采用简单的单峰，往往呈现出多峰性态。笔者拟由密度变换解获得概率密度函数的近似值，然后引入混合分布模型对其进行建模，并通过回归拟合确定关键参数，最后确定联合概率模型。

2.1 累计降雨量的条件密度变换解及其数值逼近

根据概率论可得到关系式（5）。

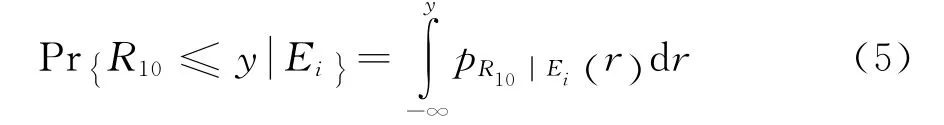
此外，若将影响R10的所有随机因素记为Θ，且R10＝H（Θ），那么式（5）左端项亦可按照式（6）计算，即

式中：ΩΘ为Θ的取值空间；I（θ，y）为示性函数，可表示为式（7）。

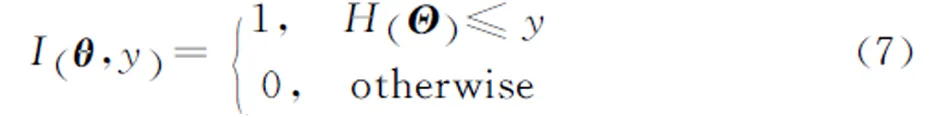
综合式（5）～（7），经简单推导可有

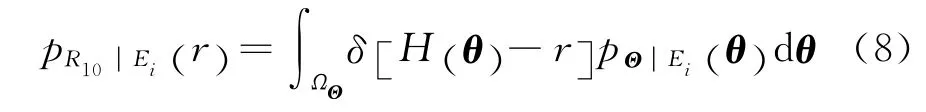
式中，δ［·］表示Diracδ函数。

式（8）描述了在条件Ei下Θ和R10之间概率结构的变换关系，文中称之为条件密度变换解。

式（8）形式简单，但并不便于应用，主要体现于3方面：1）δ［·］属于广义函数，积分计算困难；2）H（·）无显式表达式；3）Θ的条件概率密度函数未知。为此，引入正态密度函数形式的Diracδ函数序列［18］对式（8）进行数值逼近，即

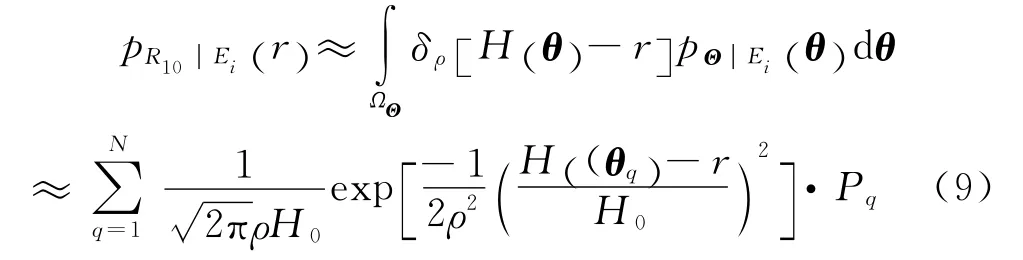
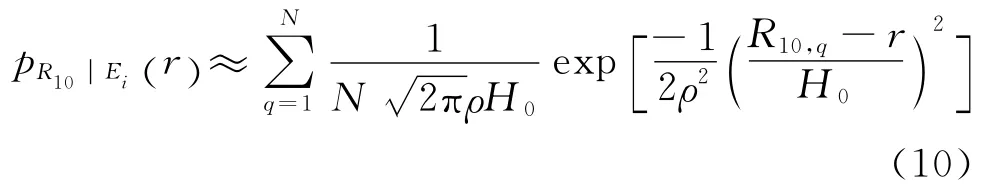
2.2 混合变量的联合概率模型

根据由式（10）获得的条件概率密度函数计算值，可采用如下的混合分布模型对其进行建模，即［19］

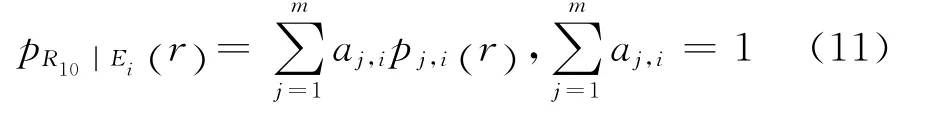
式中：pj，i（r）表示pR10｜Ei（r）的混合模型的第j个分量密度，m表示分量密度的数量，aj，i为相应的组合系数。作为探索性研究，上述参数均由试算确定。

继而，可建立日降雨量和累计降雨量的联合概率模型pEi，R10（·）如式（12）。

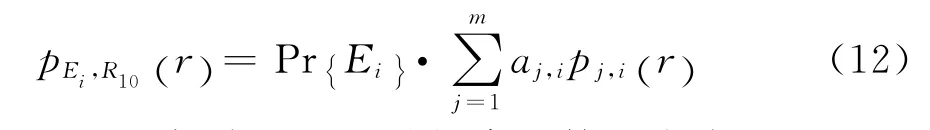
于是根据式（4），滑坡概率可简写为式（13）。

3 重庆市日降雨量与累计降雨量的联合概率结构建模

3.1 重庆市降雨资料及处理

重庆市气象局提供了重庆市自1980年至2009年共30a的小时降雨数据和2003年至2009年间的分钟降雨数据。基于以上数据可获得日降雨量和10d累计降雨量的联合观测样本共10 818条。其中，日降雨等级为小雨的样本10 007条，日降雨等级为中雨的样本530条，日降雨等级为大雨的样本211条，日降雨等级为暴雨的样本70条。

需指出的是，10 007条小雨样本中日降雨量为0且累计降雨量很小的记录占有很大比例。一方面，这样的降雨基本不会引起滑坡，另一方面，这些数据会极大地引起建模困难。例如，两者均为0的样本约占16.7%，而理论上连续随机变量取任意值的概率均为零。为简单且便于应用，对日降雨等级为小雨时累计降雨量的概率建模时仅考虑了累计降雨量超过20mm的数据，共3 763条。此时，E1发生时滑坡的概率为

式中：b1为未考虑样本占E1样本的比例，文中b1＝0.624为由剩余样本确定的条件概率密度函数，且可类似于式（12）建立其概率模型。需指出的是，式（14）的推导中将降雨等级为小雨且累计降雨量不超过20mm的样本处理为日降雨量和累计降雨量均为0的样本。由于这两类样本均不引起滑坡，所以上述处理方式不影响滑坡概率的计算。

将式（14）代入式（4）即可获得修正后的滑坡概率为式（15）所示。

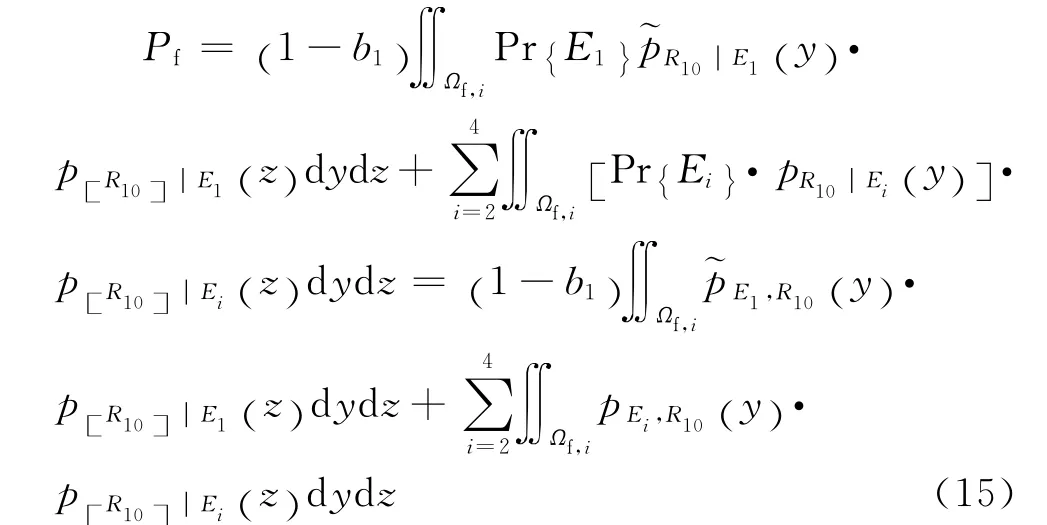
3.2 10d累计降雨量的概率密度估计

首先，利用条件密度变换解的Diracδ逼近对降雨等级为小雨实测样本中选取的3 763条累计降雨量超过20mm的样本子集进行累计降雨量的概率密度估计，结果如图1所示。为验证密度估计的准确性，将其与频数直方图和经验累积分布函数进行了对比。图1（a）和（b）分别表示与等间距直方图和等频数直方图的对比，其中等频数直方图分10个等频率区间，图1（c）表示与经验累积分布函数的比较，下同。不难发现，计算结果和三者均吻合良好。

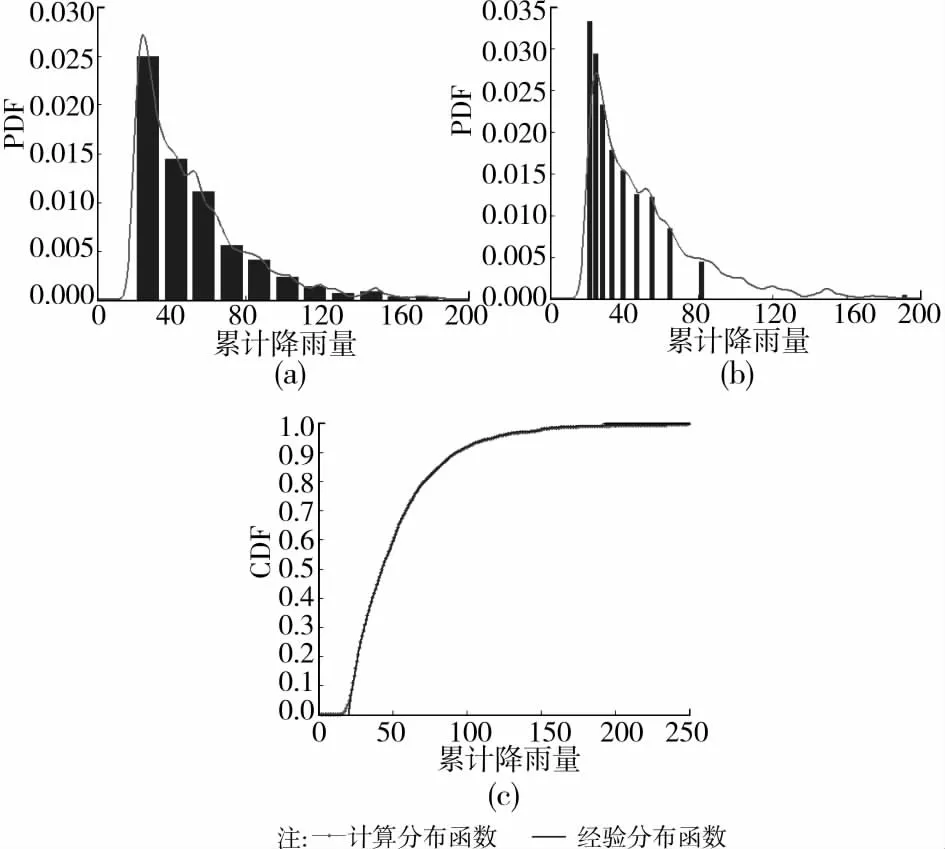
图1 日降雨等级为小雨时累计降雨量的概率密度函数

类似地，可给出降雨等级为中雨、大雨和暴雨时的密度估计，结果分别示于图2～4。通过与直方图、经验累积分布函数的比较可知上述密度估计是合理且准确的。

值得注意的是，图2中等间距直方图和等频数直方图在累计降雨较小时存在着显著差异，甚至体现于图形趋势上。究其原因在于此区间存在大量样本，在等间距直方图内均位于同一条带内，不能描述出更精细的概率变化；而等频数直方图可以较好地弥补了这一缺陷。

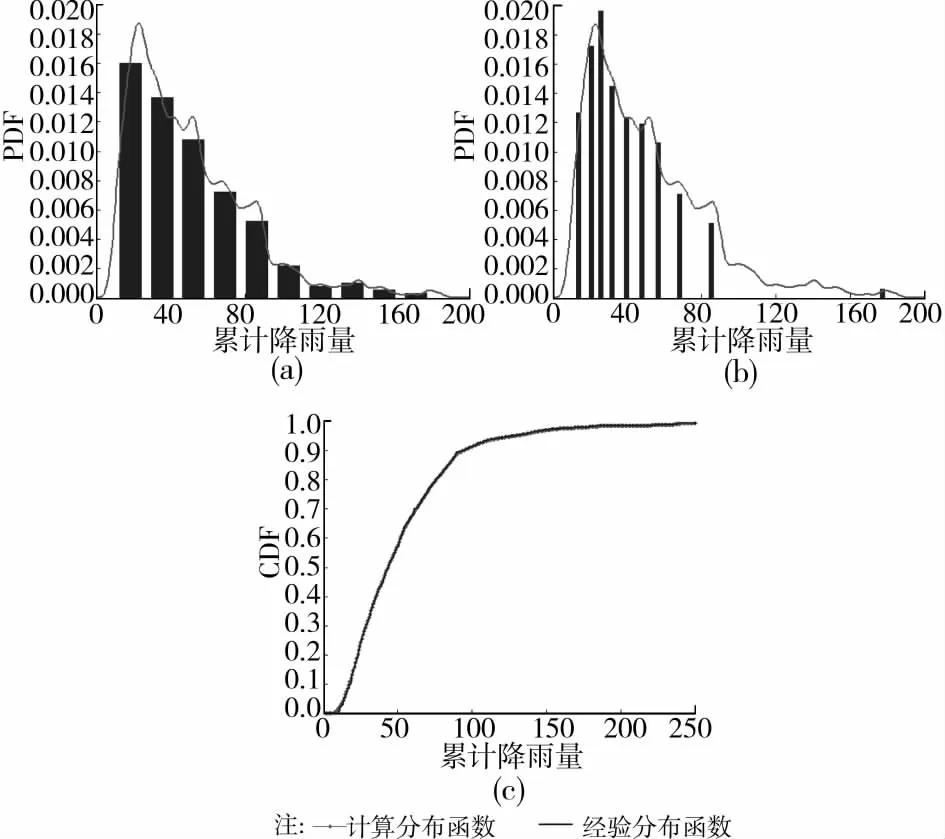
图2 日降雨等级为中雨时累计降雨量的概率密度函数

3.3 10d累计降雨量的混合分布概率模型

显然，上述密度估计值是不便于应用的，为此需建立解析的概率模型。

图3 日降雨等级为大雨时累计降雨量的概率密度函数

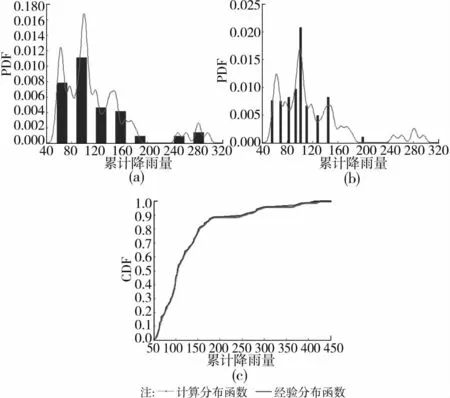
图4 日降雨等级为暴雨时累计降雨量的概率密度函数

首先，采用常用的概率模型对其进行建模。由于累计降雨量存在明显的边界（即≥0），因此，可尝试用对数正态分布和3参数Weibull分布对其进行建模，建模准则为均值和标准差一致。将不同降雨等级的建模结果与直方图、密度估计结果进行对比，分别示于图5～8，其中（a）图均为与等间距直方图的比较，（b）图则为与等频数直方图的比较。

由图5可知，3参数Weibull分布可以很好地描述降雨等级为小雨时的累计降雨量条件概率密度函数，其概率密度函数为

此模型的累积分布函数与经验累积分布函数的比较示于图9，吻合良好。

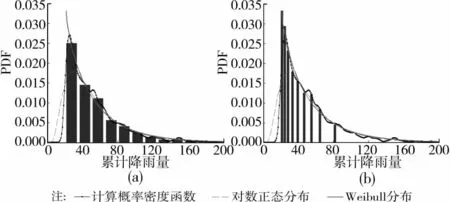
图5 日降雨等级为小雨时累计降雨量的概率密度函数计算值与对数正态分布和Weibull分布的比较

图6 日降雨等级为中雨时累计降雨量的概率密度函数计算值与对数正态分布和Weibull分布的比较

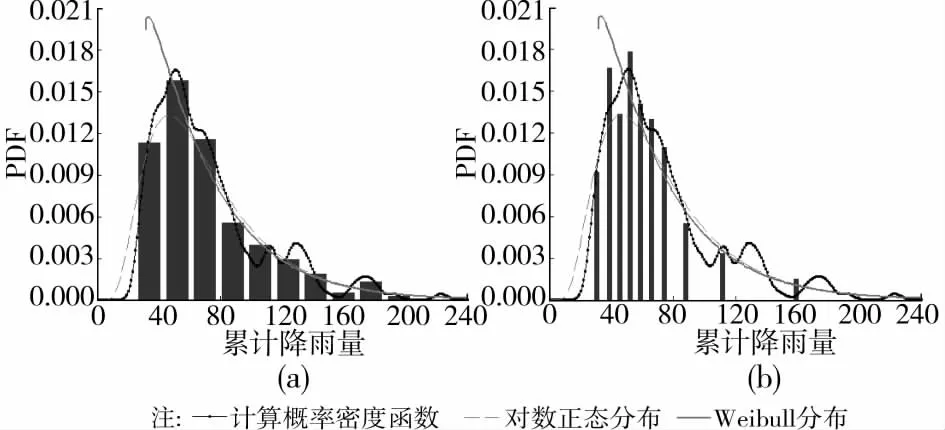
图7 日降雨等级为大雨时累计降雨量的概率密度函数计算值与对数正态分布和Weibull分布的比较

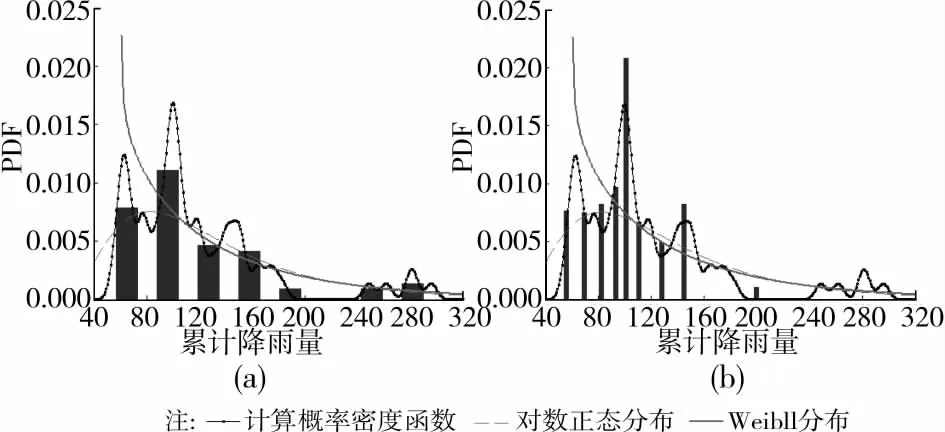
图8 日降雨等级为暴雨时累计降雨量的概率密度函数计算值与对数正态分布和Weibull分布的比较

图6和图7表明此2种情形对数正态分布较Weibull分布更接近于计算结果，但效果均不理想；图8表明降雨等级为大暴雨时无论是对数正态分布还是Weibull分布均与实际分布相差太远。为此需要采用式（11）所描述的混合模型对此三者进行建模。

根据试算，可得到降雨等级分别为中雨、大雨和暴雨时累计降雨量的混合模型分别为式（17）、（18）、（19）。

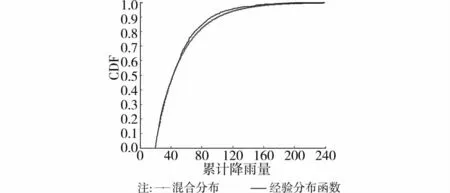
图9 日降雨等级为小雨时模型的累积分布函数与经验累积分布函数的比较

各模型与相应的直方图以及经验累积分布函数的比较示于图10～12。不难发现，较常用的单峰概率模型，混合模型的建模效果更为理想。

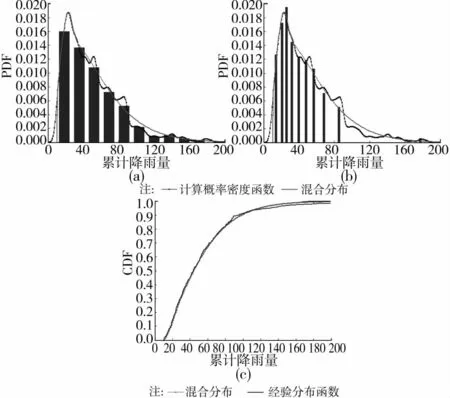
图10 日降雨等级为中雨时模型与等间距直方图、等频数直方图和经验累积分布函数的比较

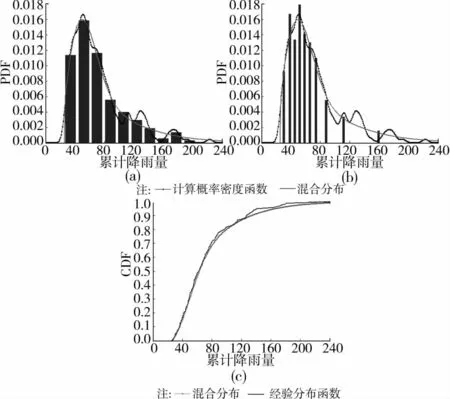
图11 日降雨等级为大雨时模型与等间距直方图、等频数直方图和经验累积分布函数的比较

图12 日降雨等级为暴雨时模型与等间距直方图、等频数直方图和经验累积分布函数的比较

3.4 联合概率模型

由式（12）可知，欲建立日降雨量与累计降雨量的联合概率结构，除累计降雨量的条件概率密度模型外，尚需确定Pr｛Ei｝。根据降雨实测数据，可统计出不同降雨等级的频度函数，如表1所示。

将表1的频度函数和第3.3节累计降雨量的条件概率密度模型代入式（12）即可得到重庆市日降雨量和累计降雨量的联合概率模型。

表1 降雨等级的频度函数

4 结 论

降雨型滑坡的概率分析和预测中，作为主要输入的降雨是关键参数。笔者以日降雨量和累计降雨量为降雨量的控制参数，结合重庆气象局提供的降雨观测数据，建立了日降雨量和累计降雨量的联合概率模型。与经典意义上的联合概率结构不同，文中沿用降雨型滑坡分析的习惯，将日降雨量视为离散变量，而累计降雨量为连续变量。在此基础上导出了离散变量和连续变量的联合概率模型和条件密度变换解及其Diracδ函数序列逼近，并提出了基于上述计算结果建立可用的联合概率模型的思路。然后，将上述思路用于重庆市的降雨数据，建立了适用于重庆地区的日降雨量和累计降雨量的联合概率模型。

值得指出的是，文中借鉴可靠度概念建立的滑坡概率分析方法思路清晰、简单、直接，但相比较而言，对相关数据的要求却更为严格，除了降雨量的概率模型之外，尚需获得降雨阈值的概率结构。

［1］李长江.降雨型滑坡预报的理论、方法及应用［M］.北京：地质出版社.2008.

［2］Montgomery D R，Dietrich W E.A physically based model for topographic control on shallow landsliding［J］.Water Resources Research，1994，30：1153－1171.

［3］Wu W，Sidle R C.A distributed slope stability model for steep forested basins ［J］.Water Resources Research，1995，31：2097－2110.

［4］Dietrich W E.A process－based model for colluvial soil depth and shallow landsliding using digital elevation data［J］.Hydrological Processes，1995，9（3／4）：383－400.

［5］Montgomery D R，Sullivan K，Greenberg H M.Regional test of a model for shallow landsliding ［J］.Hydrological Processes，1998，12：943－955.

［6］Iverson R M.Landslide triggering by rain infiltration［J］.Water Resources Research，2000，36（7）：1897－1910.

［7］Borga M.Assessment of shallow landsliding by using a physically based model of hillslope stability ［J］.Hydrological Processes，2002，16：2833－2851.

［8］Casadei M，Dietrich W E，Miller N L.Testing a model for predicting the timing and location of shallow landslide initiation in soil－mantled landscapes［J］.Earth Surface Processes and Landforms，2003，28：925－950.

［9］Tsai T L，Yang J C.Modeling of rainfall－triggered shallow landslide［J］.Environmental Geology，2006，50：525－534.

［10］Guzzetti F.Rainfall thresholds for the initiation of landslides in central and southern Europe ［J］.Meteorology and Atmospheric Physics，2007，98（3／4）：239－267.

［11］林孝松.滑坡与降雨研究［J］.地质灾害与环境保护，2001，12（3）：1－7.LIN Xiaosong.The study of landslide related to rainfall［J］.Journal of Geological Hazards and Environment Preservation，2001，12（3）：1－7.

［12］张友谊，胡卸文，朱海勇.滑坡与降雨关系研究展望［J］.自然灾害学报，2007，16（1）：104－108.ZHANG Youyi，HU Xiewen，ZHU Haiyong.Prospect of research on relationship between landslide and rainfall［J］.Journal of Natural Disasters，2007，16（1）：104－108.

［13］张珍，李世海，马力.重庆地区滑坡与降雨关系的概率分析［J］.岩石力学与工程学报，2008，24（17）：3185－3191.ZHANG Zhen，LI Shihai，MA Li.Probability analysis of relationship between landslide and rainfall in Chongqing area ［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（17）：3185－3191.

［14］李汝成，王复明.降雨入渗对泥岩 土混填路堤稳定性的影响［J］.岩石力学与工程学报，2008，27（11）：2260－2266 LI Rucheng，WANG Fuming.Effect of rainfall infiltration on stability of mudstone－soil mixture embankment［J］.Chinese Journal of Rock Mechanics and Engineering，2008，27（11）：2260－2266.

［15］王军.降雨入渗对流变介质隧道边坡稳定性的分析［J］.岩土力学，2009，30（7）：2158－2162，2167 WANG Jun.Analysis of stability of tunnel－slope with rheological medium under rainfall infiltration［J］.Rock and Soil Mechanics，2009，30（7）：2158－2162，2167.

［16］张卢明.降雨入渗对滑坡渗流场和稳定性的影响分析［J］.铁道工程学报，2009（7）：15－19.ZHANG Luming.Effects analysis of rainfall infiltration on the landslide seepage field and stability［J］.Journal of Railway Engineering Society，2009，7：15－19.

［17］Crozier M J.Prediction of rainfall－triggered landslides：a test of the antecedent water status model［J］.Earth Surface Processes and Landforms，1999，24：825－833.

［18］范文亮，李杰.广义密度演化方程的δ函数序列解法［J］.力学学报，2009，41（3）：398－409.FAN Wenliang，LI Jie.Solution of generalized density evolution equation via a family ofδsequences ［J］.Chinese Journal of Theoretical and Applied Mechanics，2009，41（3）：398－409.

［19］McLachlan G J，Peel D.Finite mixture models［M］.John Wiley ＆Sons，Inc..2000.