静力非线性方法用于桥梁高墩抗震性能分析

李正英，党朋朋，李竟涛

（重庆大学a.土木工程学院；b.山地城镇建设与新技术教育部重点实验室，重庆400030）

非线性静力分析（Pushover）法是一种简化的非线性地震反应评估方法，其基本原理是：在结构分析模型上施加按某种方式分布的侧向荷载模拟地震作用下的侧向分布力，并逐级按比例增大，直到结构达到预定的状态（位移超限或位移达到目标位移），然后评估结构的性能。它提供了一种评估结构地震反应尤其是非线性地震反应的简单而有效的方法，因此Pushover分析法为各国规范所接受，中国建筑结构抗震设计规范也引入了Pushover分析方法［1］。

Pushover分析方法中，侧向荷载的分布模式直接影响分析结果，目前规范常用的侧向荷载分布模式有均匀分布荷载、倒三角荷载、一阶振型荷载等，已有研究结果表明采用上述水平侧向力分布模式难以反映高阶振型对结构地震反应的影 响［2－4］。Chopra等基于结构动力学多自由度体系解耦的思想提出了模态Pushover分析法（MPA）［5］。MPA 法采用基于振型的侧向加载模式，将多自由度体系的反应等效为多个单自由度体系反应结果的组合，考虑了高阶振型的影响，与传统的Pushover方法相比精度有所提高。以上Pushover分析方法大多是针对建筑结构提出的，应用于桥梁结构的研究相对较少。由于桥梁结构的非规则性及其自身特殊性而与一般建筑结构有较大区别，因此有必要对Pushover方法在桥梁结构上的应用加以细致研究。而且对于桥梁中的高墩桥梁，由于墩高而使得高阶振型的影响更明显，因此MPA方法在高墩及高墩桥梁抗震性能评估中应用的有效性有待研究［6］。

笔者基于MPA法的基本思路，并引入振型有效高度［7］的概念，提出了改进的 MPA法（MMPA），通过计算各阶振型的有效高度作为Pushover分析中的加载控制点，而传统Pushover法是以结构顶点作为加载控制点。选取30、90m单墩作为研究对象，采用MMPA法、MPA法和FEMA建议的2种Pushover法进行非线性静力分析，并将分析结果与非线性时程分析结果相比较，以对非线性静力分析法用于桥梁高墩抗震性能评估的有效性进行研究。

1 MPA法及改进的MPA法

MPA采用基于振型的侧向加载模式，考虑了高阶振型的影响，与传统的Pushover方法相比精度有所提高，其基本实施步骤如下：

1）计算结构弹性状态下各振型的频率ωn和振型向量φn；

2）对第n阶模态，施加侧向荷载s＊n＝mφn，（其中m为结构的质量矩阵）得到Pushover能力曲线（底部剪力顶部位移曲线Vbnurn）；

3）对第n阶模态，将能力曲线简化为双折线，如图1（a）所示；

4）对第n阶模态，用公式（其中，M＊n为等效振型质量，φrn第n振型顶部振型值，为第n振型的振型参与系数）将简化的能力曲线转化为等效单自由度体系的Fsn／Ln－Dn关系曲线，如图1（b）所示；

5）求解4）中等效单自由度体系的峰值位移响应Dn（可采用非弹性反应谱法或时程分析法）；

6）利用公式Urn＝ΓnφrnDn得到第n振型结构顶部峰值位移响应；

7）由Pushover分析结果得到第n振型的其它峰值反应量rn；

8）对前N阶振型（一般考虑振型质量参与系数达到95%即可）重复步骤3）～7）得到相应振型的各反应量；

9）利用SRSS规则将各振型的相应反应量组合得到结构的总反应量。

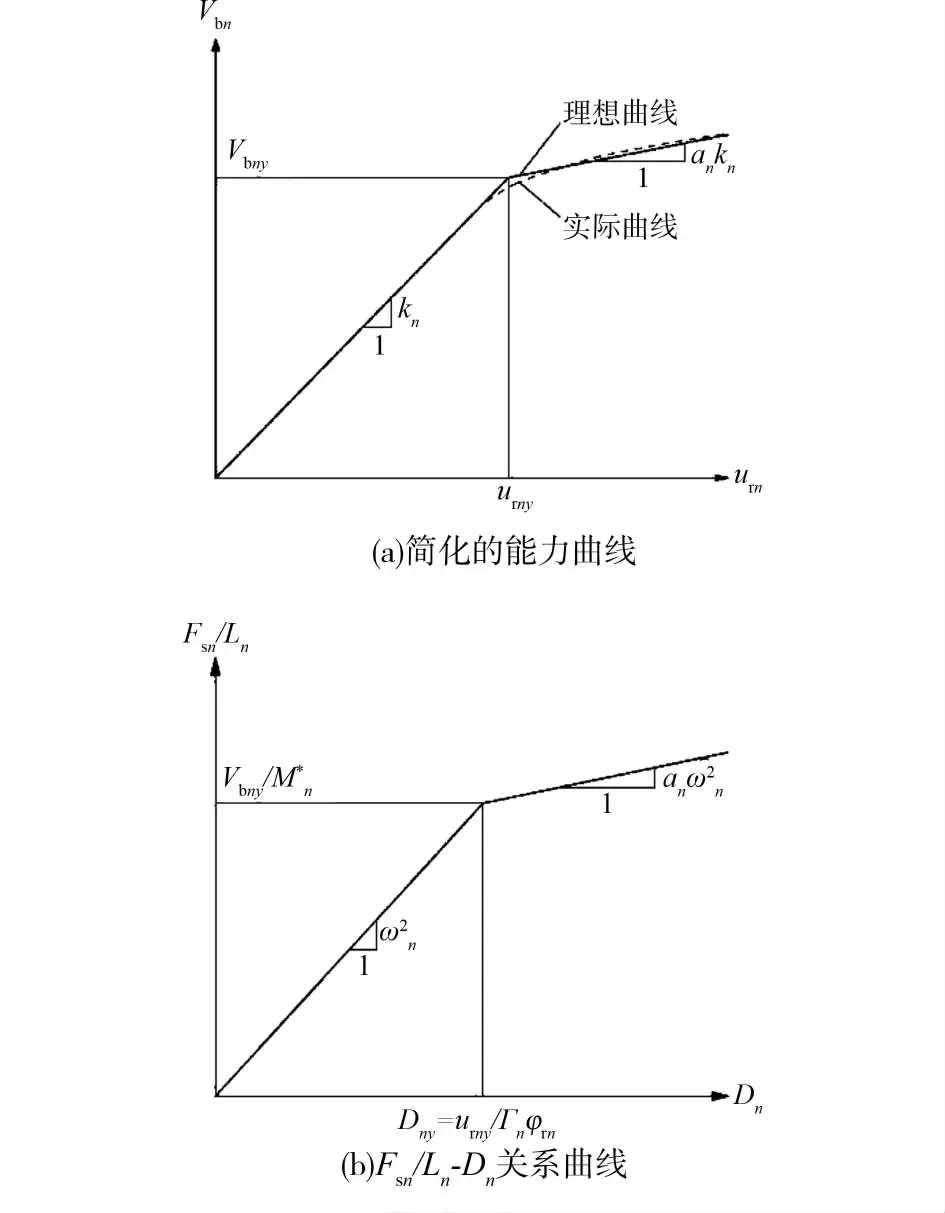
图1 第n振型等效单自由度体系能力曲线

在上述MPA方法计算步骤中，以结构顶点作为控制点，通过逐步增大侧向荷载使结构的顶部位移达到预定的目标位移。由于高柔的桥墩在水平荷载作用下以弯曲型破坏为主，高阶振型的影响较大，各振型均以结构顶点作为加载控制点，往往不能取得较好的分析效果。考虑到振型高度本质上反映的是各振型对结构总底部弯矩的贡献，是以控制结构底部总弯矩为依据［7］，因此以各振型的等效振型高度作为加载控制点，可以更为精确的模拟地震反应的结果。

为此，在MPA法的基础上进行改进，引入有效振型高度的概念：

其中HEi为有效振型高度，是具有长度的量纲；｛h｝＝｛h1，h2，…，hn｝为各节点高度向量。在改进 MPA 法中，以各振型有效振型高度处的节点作为控制点，逐步增大侧向荷载使控制点的位移达到预定的目标位移。

为便于对比分析，另选取了FEMA－356建议2种类型的侧向加载模式［8］，即基于基本振型的侧向加载模式（1st）和均布侧向加载模式（Uniform），与前述2种静力非线性分析方法对比研究。

2 目标位移的确定

Pushover方法是通过对结构施加沿高度呈一定分布的水平单调递增荷载来将结构推至某一预定的目标位移，来分析结构的薄弱部位及其它非线性状态的反应，以判断在未来可能地震作用下结构及构件的变形能力是否满足设计及使用功能的要求。因此确定目标位移是基于性能的抗震设计的关键之一。目前，计算结构目标位移的方法主要有能力谱方法和对多自由度体系或等效单自由度体系的弹塑性时程分析方法。而对于模态Pushover分析方法，需要确定结构在各振型等效侧向力作用下的目标位移，笔者基于弹塑性时程分析，采用文献［9］中的方法求解目标位移。首先选取合适的地震波，计算结构的弹塑性位移反应，得到结构控制点的水平位移向量时程。然后根据式（2）～（3）求得结构第n阶振型的目标位移：

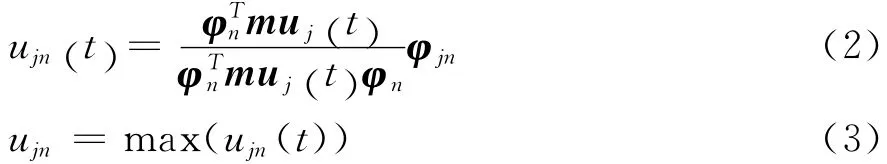
其中，ujn为第n振型j节点（改进MPA方法中为有效振型高度处的控制节点）的目标位移，ujn（t）为结构j节点t时刻水平位移在第n振型上的分量，uj（t）为结构j节点在t时刻的水平位移向量。

为了排除目标位移不同带来的计算误差，FEMA－356建议的2种加载模式分析中，目标位移取上述方法求得的结构顶点处各阶振型目标位移的SRSS组合。

3 计算模型

采用的计算模型为30m和90m2个单墩，分别作为中低墩和高墩的代表。墩底固结，墩身质量集中在相应节点上，与墩柱相邻跨的上部结构质量M集中在墩顶处，其截面形式和基本参数见图2。墩身采用弹塑性纤维梁柱单元模拟，其中混凝土纤维本构模型采用Kent－Park模型［10］，其应力 应变关系如图3所示。钢筋纤维采用双直线模型。单元沿墩高的划分情况为：30m墩单元长度为1m，90m墩单元长度为2m。由弹性分析求得的单墩基本动力参数及按等效振型高度确定的加载控制点位置见表1。

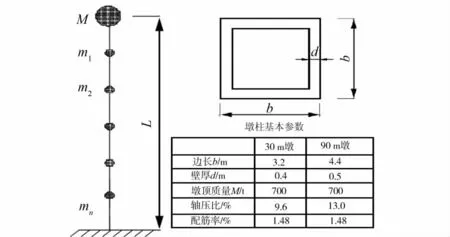
图2 单墩模型及基本参数

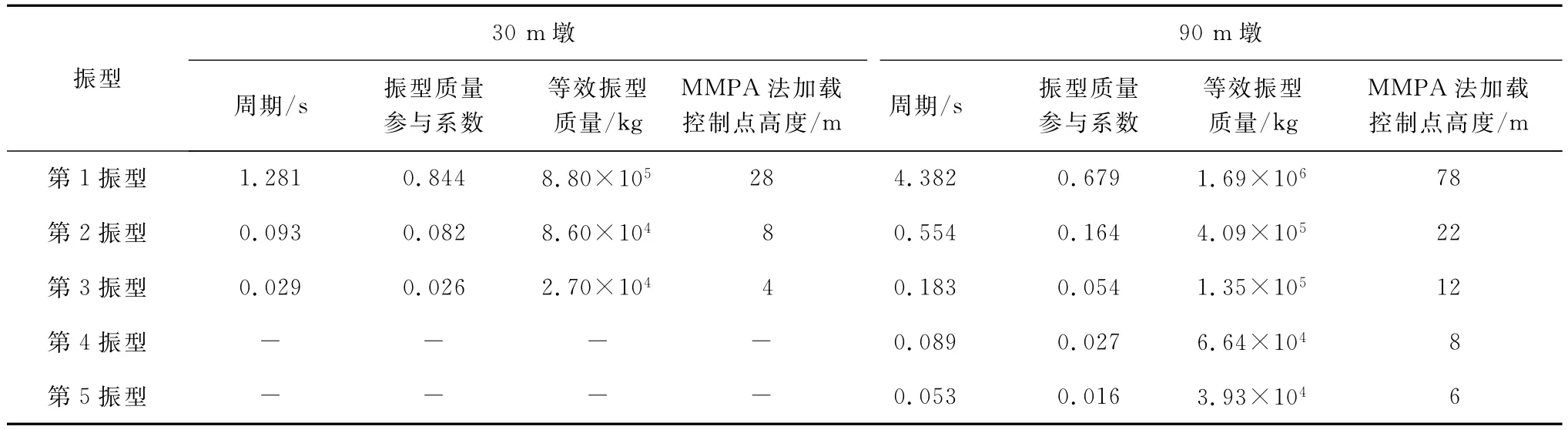
表1 墩柱基本动力参数

表2 地震波记录

续表2

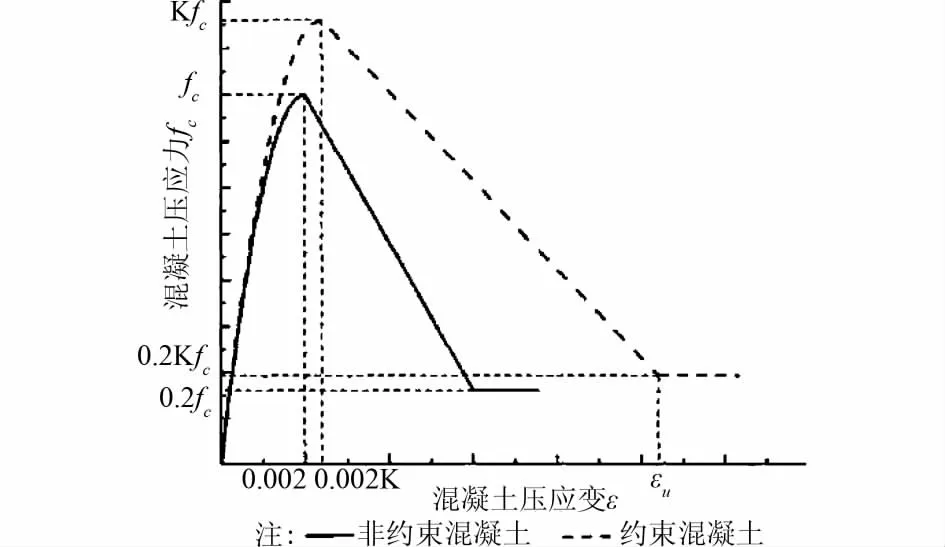
图3 Kent－Park混凝土应力 应变关系曲线

非线性动力时程分析共选用8条地震波，数据来源于美国太平洋地震工程研究中心（PEER）。为了保证结构进入屈服状态，在进行弹塑性分析时30m墩地震动峰值加速度调整为0.5g，90m墩地震动峰值加速度调整为1.0g。图4为将地震波峰值加速度（PGA）统一调整至0.5g时的加速度谱。

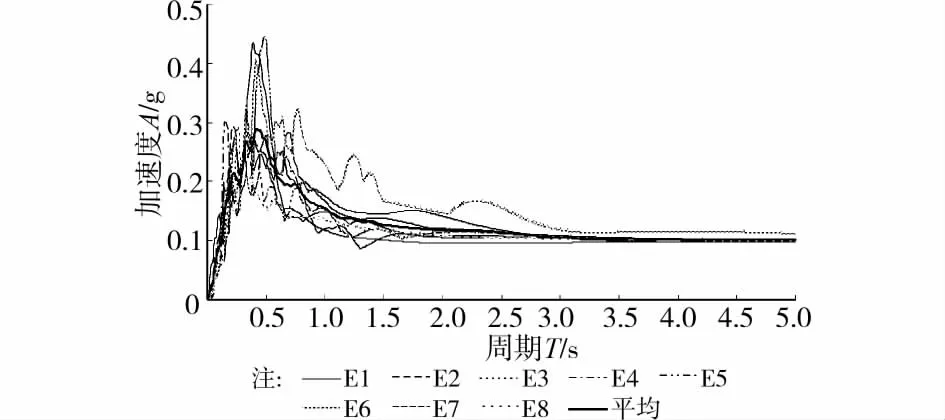
图4 地震波反应谱及平均反应谱

Pushover分析及非线性时程分析过程基于OpenSees（Open System for Earthquake Engineering Simulation）［11］软件平台，并采用 Tcl／Tk脚本语言编程后处理。

4 结果分析

由于地震动的随机性，单条波的对比分析并不能准确说明计算结果的优劣性，因此计算结果取为8条地震动作用下的平均值。考察结构的峰值位移响应、峰值节点间位移角响应及单元杆端峰值曲率响应。其中节点间位移角为相邻两节点的水平位移差与节点高度差的比值：

式中，uj、ui分别为节点j、i在地震作用下的水平位移，Hj、Hi是节点j，i的高度。

4.1 峰值位移响应评价

图5为30m墩在0.1g、0.5g地震动作用下，90m墩在0.1g、1.0g地震动作用下时程分析和不同侧向力加载模式Pushover分析所得节点峰值位移反应及误差对比。其中30m墩在0.1g地震动作用下墩顶最大平均位移为3.7cm，结构处于弹性阶段；0.5g时墩顶最大平均位移为15.8cm，处于弹塑性阶段。90m墩在0.1g地震动作用下墩顶最大平均位移为3.7cm，结构处于弹性阶段；1.0g时墩顶最大平均位移为44.1cm，处于弹塑性阶段。图中，DHA、1st、Uniform、MPA、MMPA分别代表动力时程推覆分析和基于基本振型的侧向加载模式、均布侧向加载模式的Pushover分析以及模态Pushover、改进的模态Pushover分析方法得到的结构反应。

由图5可知，对30m墩而言，当地震动强度较小时，4种Pushover分析法的计算结果与时程分析法的误差在3%以内，精度较高；相对地，在结构底部各节点处均布侧向加载模式的计算误差较大。MMPA法求得的30m墩顶部目标峰值位移误差略大于其它3种Pushover法的计算结果，其原因在于30m墩墩身质量相比于墩顶质量较小，地震反应以一阶振型为主，因而以顶点位移作为控制点的MPA方法或基于基本振型的侧向加载模式已可得到较好的分析结果。而MMPA法第一振型的控制点位于28m高度处而非墩顶，由此会带来一定的计算误差，

此外，SRSS组合方式也可能是导致误差过大的原因。可见，对于30m墩为代表的低墩，高阶振型的影响并不明显，因此在进行非线性静力分析时可采用基于基本振型的侧向加载模式的Pushover的分析方法即可。

对于90m墩，由于MPA法和MMPA法考虑了高阶振型的影响，其计算结果明显优于只考虑第一振型的1st加载模式和Uniform加载模式；当地震动强度较大时，由于高阶振型作用下形成的塑性铰位于结构的中上部［12］，分析过程中当加载控制点位于结构顶部时可能会因为结构的屈服而低估高阶振型对结构反应的贡献，此时MPA法的改善效果已不明显（图5（h）），而 MMPA法按照等效振型高度确定加载控制点，控制点的高度随振型而改变，避免了因为结构屈服造成的低估高阶振型贡献的影响，因此MMPA法的计算结果较MPA法有较好的改进。

图5 单墩节点位移分布

4.2 峰值节点间位移角响应评价

图6为30m墩在0.1g、0.5g地震动作用下，90m墩在0.1g、1.0g地震动作用下时程分析和不同侧向力加载模式下Pushover分析所得节点间位移角及误差对比。

图6 单墩节点间位移角分布

由图6可知，节点间位移角误差规律与位移反应的误差规律基本一致。即，对于低墩，地震反应以一阶振型为主，各种Pushover法的计算结果与时程分析较为接近；随着墩高的增加，高阶振型的贡献的影响不能忽略，MPA法和MMPA法的计算结果明显优于其它Pushover分析法，而当地震动强度较大时，MPA法低估了高阶振型的影响，误差较大。

4.3 单元杆端曲率响应评价

图7（a）～（f）为3 0、9 0m 墩在不同地震动强度下截面曲率及误差对比。对比图5墩身节点位移和

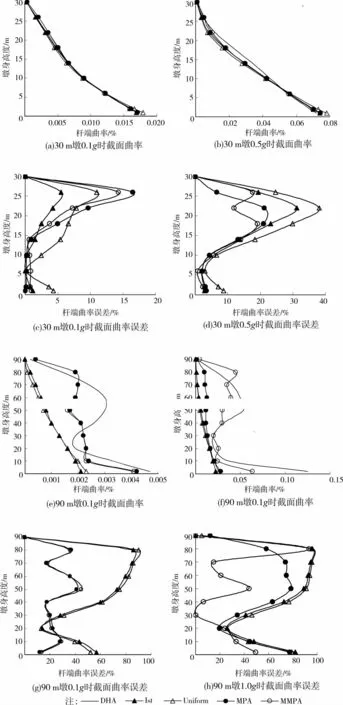
图7 单墩截面曲率分布

图7的截面曲率分布，可发现对30m的低墩，截面曲率最大值一般位于墩低截面，而且墩顶最大位移与墩底最大曲率同步出现，二者之间一一对应，因此将考察的重点放在靠近底部的各截面处。而高墩由于高阶振型的贡献增加及墩身质量效应的影响，墩身曲率分布呈较为复杂的高次曲线，在墩身中部也可能出现曲率较大的情况（图7（e）、（f）说明了这一点）。已有研究也表明［13］，高墩的墩顶最大位移与墩底最大曲率常常会不同步出现，位移大时损伤不一定严重，对于高墩而言截面曲率比位移有更能体现结构的性能。

由图7（a）～（d）可知，除均布侧向加载模式外，其它3种加载模式都能较为准确的模拟墩低截面处的曲率，其误差在5%以内，这进一步证明了前述结论。图7（e）～（h）为90m墩pushover分析和时程分析墩身截面曲率及其误差对比，由图可知，MPA法和MMPA法的计算结果明显优于只考虑第一振型的一阶加载模式和均布侧向加载模式；当地震动强度较大时，MMPA法能较好地改善底部截面的曲率误差。

5 结 论

基于MPA法的基本思路并引入振型有效高度的概念提出了改进的 MPA法（MMPA），以30、90 m单墩作为研究对象，采用MMPA法、MPA法和FEMA建议的2种Pushover法进行非线性静力分析，以节点位移、节点间位移角、截面曲率作为分析指标，将分析结果与非线性时程推覆分析结果相比较。对4种Pushover分析法应用于桥梁高墩性能评估有效性做了对比分析，得出以下结论：

1）以30m墩为代表的低墩，其地震反应以一阶振型为主，高阶振型的影响不大，进行非线性静力分析时，采用基于基本振型的侧向加载模式的Pushover分析法和MPA法均可得到较好的计算结果。

2）以90m墩为代表的高墩，其地震反应受高阶振型影响较大，只考虑第一振型的侧向加载模式和均匀加载模式计算精度较差。而对于MPA法及MMPA法，当地震动强度较小时，MPA法和MMPA法可以较好的改善计算结果。随着地震动强度的增大，结构非线性程度增加，MPA法的改进效果已不明显，而MMPA法按照等效振型高度确定加载控制点，控制点的高度随振型而改变，避免了因为结构屈服造成的低估高阶振型贡献的影响，因此MMPA法的计算精度稍好于MPA法。

3）对于高墩而言，由于高阶振型的贡献增加及墩身质量效应的影响，分析的3个指标中，截面曲率比位移更能体现结构的性能。

在强震作用下，尽管MMPA法相对于MPA法有较好的改进，但计算精度在降低，因此对于强震下的桥梁高墩抗震性能研究，宜采用动力非线性分析法。笔者反对单墩进行了研究，静力非线性分析方法用于整桥模型的分析将是后续的研究重点。

［1］GB50011－2010建筑抗震设计规范［S］.北京：中国建筑工业出版社，2010.

［2］胡家志.浅谈静力弹塑性分析方法［J］.山西建筑，2010，36（20）：49－51.HU Jiazhi.Discussion on static elastic plastic analysis method［J］.Shanxi Architecture，2010，36（20）：49－51.

［3］高德志，徐晓龙，崔原豪.对静力弹塑性分析的抗震性能评价方法的改善［J］.建筑结构，2009，39（s）：622－625.GAO Dezhi，XU Xiaolong，CHOI Wonho.Modified method for seismic performance evaluation to pushover analysis［J］.Building Structure，2009，39（S1）：622－625.

［4］宋怀金.考虑高阶振型影响的改进的多模态推覆分析方法［J］.工程抗震与加固改造，2010，32（2）：25－30.SONG Huaijin.An improved multi－mode pushover analysis method considering the effects of high modes［J］.Earthquake Resistant Engineering and Retrofitting，2010，32（2）：25－30.

［5］Chopra A K，Goel R K.A modal pushover analysis procedure to estimate seismic demands for buildings：theory and preliminary evaluation，CMS－9812531［R］.Berkeley：Pacific Earthquake Engineering Research Center，2001.

［6］魏标，李建中.非规则桥梁的模态推倒分析［J］.振动与冲击，2011，30（2）：110－114.WEI Biao，LI Jianzhong.Modal pushover analysis of an irregular continuous bridge［J］.Journal of Vibration and Shock，2011，30（2）：110－114.

［7］孙广俊，李爱群.关于结构振型参与系数和振型贡献的分析［J］.防灾减灾工程学报，2009，29（5）：485－490.SUN Guangjun，LI Aiqun.Analysis of mode participation factor and modal contribution of structures［J］.Journal of Disaster Prevention and Mitigation Engineering，2009，29（5）：485－490.

［8］Building Seismic Safety Council（BSSC）.Prestandard and commentary for the seismic rehabilitation of buildings，FEMA－356［R］.Washington D.C.：Federal Emergency Management Agency，2000.

［9］闻奇光.模态pushover的影响因素评估及改进方法研究［D］.重庆：重庆大学，2007.

［10］Kent D C，Park R.Flexural members with confined concrete［J］.Journal of the Structural Division，ASCE，1971，97（7）：1969－1990.

［11］Mazzoni S，McKenna F，Scott M H，et al.OpenSees command language manual［M］.Berkeley：University of California，2007.

［12］Goel R K，Chopra A K.Role of higher－“mode”pushover analyses in seismic analysis of buildings［J］.Earthquake spectra，2005.21（1）：1027－1041.

［13］梁智垚.非规则高墩桥梁抗震设计理论研究［D］.上海：同济大学，2007.