砂卵石地层盾构开挖面稳定性分析
2012-08-11白永学漆泰岳吴占瑞
白永学,漆泰岳,吴占瑞
(西南交通大学 土木工程学院,成都610031)
随着成都地区经济快速发展,交通拥挤问题日渐突出,修建地铁成为解决交通拥挤问题的重要手段。成都平原为典型的冲积扇平原,上覆地层以砂卵石土为主,成都地铁1、2号线区间大部分从砂卵石土层中穿越。砂卵石地层力学特性比较复杂,盾构施工控制难度大,经常出现超出土现象,导致地面塌陷事故时有发生,仅在地铁1号线人民路延线就发生过多次地面塌陷,曾引发房屋基础悬空和出租车掉入空洞内等事件。地面塌陷的根本原因是开挖面失稳而造成出土量过大而引起的;因此,在砂卵石地层中开挖面稳定性问题成为该地区盾构施工的关注焦点。
开挖面稳定性的研究方法主要包括理论分析、模型试验和数值计算3种方法。盾构开挖面稳定性理论分析方法主要有2类:基于上、下限定理的极限分析法和基于滑动面上力与力矩平衡的极限平衡法[1-3]。理论研究的影响因素比较少,因此应用范围受到局限,且结论和实际情况有时出入较大。Chambon等[4]、Mair等[5]对开挖面的稳定性进行了离心模型试验,分别对粘土地层和砂土地层开挖面的破坏形状进行了研究,并阐述了深度对极限支护压力的影响。程展林等[6]通过小型模型试验研究了拱效应和孔隙水压对盾构开挖面稳定性的影响,并提出中粗砂地层中临界泥浆支护压力公式。由于模型试验费用高、耗时长,研究多因素对开挖面稳定性的影响很困难,得出系统的结论则更加困难。数值计算方法能够研究多因素影响下的开挖面稳定性,并相对容易得出系统结论,因而被国内外学者广泛应用。数值计算方法主要包括有限差分法、有限元法和颗粒离散元法等,秦建设等[7]、黄正荣等[8]、乔金丽等[9]使用有限差分FLAC3D程序对开挖面稳定性进行了研究,Karim[10]应用三维颗粒离散元法对Chambon砂土的离心试验[4]进行模拟,模拟结果与试验结果较吻合。王明年等[11-12]采用颗粒离散元法对砂卵石的开挖面稳定性进行了研究。
笔者在众多学者研究的基础上,通过大型三轴试验研究了砂卵石层的力学特性,选用颗粒离散元法进行数值计算,通过对大型三轴试验进行数值计算,对砂卵石层的宏观力学参数进行细观参数的标定。编制位移显示程序,研究了开挖面变形和破坏形状,并结合地铁1、2号线施工实际情况对开挖面稳定性进行了相应分析和研究。
1 成都卵石地层地质情况
1.1 工程地质情况
成都平原地处川西平原岷江水系Ⅰ、II级阶地,为侵蚀 堆积阶地地貌,地形平坦,地表多为第四系人工填筑()杂填土,卵石土主要为全新统冲积层()和上更新统冲洪积层(),基岩埋深较深。砂卵石层主要地质特征为:
1)卵石含量高,含量在50%~85%之间,以亚圆形为主,少量圆形,分选性差,粒径以20~80mm为主,充填物为细砂和中砂。
2)卵石粒径大,部分粒径大于100mm,随机分布漂石,大粒径漂石主要分布在Q3地层中,含量一般在10%~15%。漂石粒径根据盾构施工和基坑开挖情况,最大粒径极个别达到1m以上。
3)卵石单轴抗压强度高,普遍为55~165MPa。
4)卵石层中含砂量(0.075mm<d<2.000mm)高,含砂量大致为20%~40%;含泥量少,含泥量(d<0.075mm)低于5%,属无粘性颗粒土。
5)不同粒径颗粒的含量分布不均匀,主要表现为大粒径卵石含量高,含砂量高,而圆砾(2~20mm)含量低,因而为级配不良的砂卵石土层。
6)在任意地质年代卵石层中均可能有透镜体砂层,厚度达1~2m。
1.2 水文地质概况
地下水主要为卵石层中的孔隙潜水,孔隙水主要赋存于砂卵石土层中,砂卵石层含水丰富,渗透系数在15~25m/d之间,为强透水层。
成都市降雨量丰富,是地下水的主要补给源,同时,雨洪期河水及附近沟渠也是其补给源。根据区域水文地质资料,成都地区丰水期一般出现在7~9月份,枯水期12、1、2月份,其中8月份地下水位埋深最浅,其余月份为平水期。在天然状态下,区内枯水期地下水位埋深3.0~6.0m;洪水期地下水埋深2.5~4.0m,水位年变化幅度一般在1.0~3.0m之间。
2 成都砂卵石土的大型三轴试验
2.1 试验方法
试验采用直径为300mm、高为600mm的大型三轴剪力仪进行,考虑到盾构实际埋深主要为10~30m,试验时确定最大围压为400kPa,试样允许最大粒径为60mm。试样采用振动压实法成型,将制备好的试样分6层用振动压实方法装填。试验设计干密度为2.18g/cm3,进行非饱和条件下的固结排水试验,其中土样为现场所取土样。试验破坏标准为:当应力 应变曲线出现峰值时,取峰值点为破坏点;当应力 应变曲线无峰值时,取应变15%所对应的点为破坏点。
2.2 试验材料
试验材料取自成都地铁2号线沿线埋深8~10m的稍密卵石层,试验采用天然级配作为控制级配,采用天然干密度作为试验控制密度。在现场筛分试验中,颗粒粒径最大值为220mm,其颗粒粒径分布特征指标不均匀系数Cu=106.5,曲率系数Cc=16.7,为级配不良的砂卵石土层。材料中含泥量(d<0.075mm)低于5%,属无粘性颗粒土。
由于室内试验室设备尺寸的限制,不可能同比例的进行室内试验,需要对超粒径部分进行处理,试验采用等量替代法对粒径大于60mm的颗粒进行替换,保持5mm以下细颗粒含量不变,试验级配见表1。
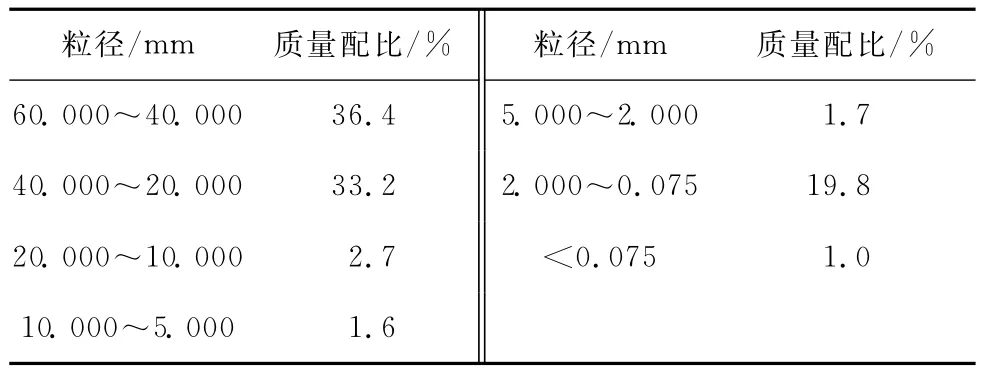
表1 试验级配
2.3 大型三轴试验成果与分析
2.3.1 应力 应变关系特性 稍密卵石试样在100、200、300、400kPa围压下的偏应力 轴向应变曲线见图1。可以看出,在围压较小时,应力 应变曲线为应变软化型;随着围压的升高,颗粒移动的阻力增加,应力应变曲线变为应变强化型,其规律符合砂卵石地层变形的一般规律[13]。试验结果按照线性Mohr-Coulomb定律得到的强度包络线如图2所示,土体的宏观力学参数见表2。
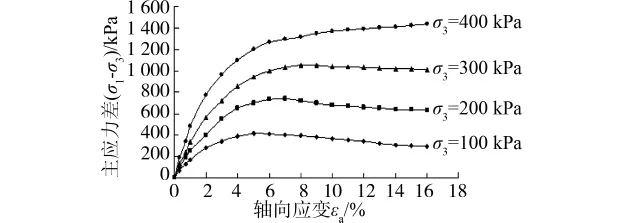
图1 偏应力 轴向应变曲线
图2 压缩试验中的线性摩尔包络圆

表2 稍密卵石的宏观力学参数
3 盾构开挖面稳定性的数值计算模型
成都砂卵石土具有粘聚力低、地层松散、强烈离散的特性,盾构施工开挖面容易产生颗粒流动现象,因此选用颗粒离散元法进行数值计算。
颗粒离散元法以单个颗粒为基本单元,颗粒之间相互作用,在计算中对每个颗粒建立运动方程,应用力 位移定律和牛顿第二定律,通过差分法求解一个微小时段的速度和位移,并对时域进行积分,由此计算出颗粒体的平动、转动、分离和大变形等问题[14-16]。
3.1 数值计算模型
模型尺寸为30m×22m×15m,盾构外直径为6m,开挖直径为6.28m,埋深为10m。在数值计算模型中,地表面为自由面,四周采用变形约束条件,管片采用wall单元模拟,为便于观察开挖面的变形破坏过程,本文编制了相应的位移显示程序。模型采用81 012个颗粒进行模拟,数值模型如图3所示。

图3 数值计算模型图
在数值计算中,假设作用于开挖面的支护压力为梯形荷载,取开挖面中心点的支护压力为代表值,为与静止土压力进行比较,引入支护压力比λ:

式中:σs为开挖面中心处的支护压力,σ0为盾构中心处水平静止土压力。
3.2 颗粒离散元细观参数标定
在颗粒离散元程序中,需要输入颗粒的细观参数,而颗粒的细观参数与土体的宏观力学参数没有明确的对应关系。为了建立土体宏观力学参数和颗粒离散元细观参数的对应关系,通常应用三轴数值试验进行标定,使三轴数值试验和试验室的结果相一致。
3.2.1 三轴数值试验模型 三轴数值试验计算过程主要包括生成试样、挤密和加载3个过程。模型外围由墙体单元合围而成,侧向墙体单元模拟围压,上、下墙体单元模拟压板,计算模型见图4。
图4 压缩试验的模型
在加载过程中始终保持围压不变,通过控制上下2个墙元的移动来模拟试样加载。在整个加载过程中,墙体的移动速度通过伺服系统进行控制,以便使围压控制在设定值,而加压也实现缓慢加载。
在颗粒离散元中,通过颗粒的接触本构模型来模拟土体宏观力学特性。接触本构模型由刚度模型、滑动模型及连接模型组成[17-19]。刚度模型给出了接触力和相对位移的弹性关系;滑动模型提供了接触颗粒发生相对移动的力学模型;粘结模型则给出了接触颗粒之间的最大抗拉和抗剪强度。通过调整接触本构模型的细观参数,可以模拟材料各种复杂的力学特性。
3.2.2 细观参数的标定结果 利用上述三轴数值模拟试验,在围压100、200、300、400kPa下,得到的偏应力 轴向应变曲线与室内试验曲线的对比,如图5所示。
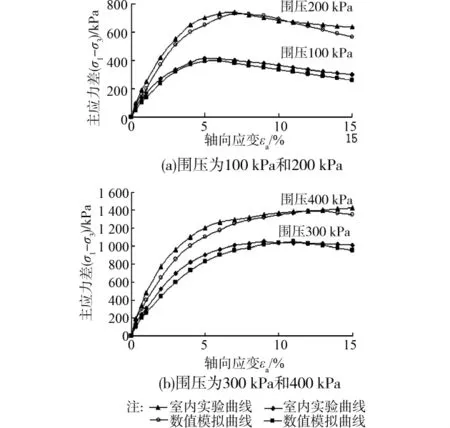
图5 数值试验与室内试验应力 应变曲线比较
通过三轴数值试验和室内试验的应力 应变曲线的对比,综合考虑内摩擦角、变形模量、泊松比等因素,经过反复调整颗粒的细观参数,使模型的细观参数与材料的宏观力学参数相一致,得到的细观参数见表3。

表3 离散元模型的细观力学参数
4 开挖面稳定性的计算分析
砂卵石地层盾构施工的主要问题是如何控制过量出土,而开挖面失稳是过量出土的根本原因。因此,主要分析极限支护压力、地表沉降、土体应力变化和开挖面破坏模式等问题。
4.1 支护压力和最大水平位移的关系
盾构施工引起开挖面附近土体的应力释放,从而导致开挖面周围土体发生位移,通过监测开挖面的位移,得到支护压力与开挖面附近土体最大水平位移关系,如图6所示。
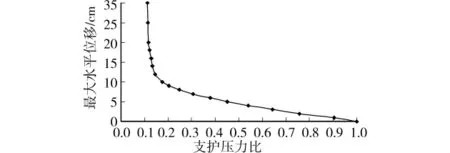
图6 支护压力比和最大水平位移的关系
从该图中可以看出,当支护压力比λ=1.0~0.2时,随着支护压力比的减小,开挖面的位移逐渐加大;开挖面的最大水平位移的变化表现为线性规律,这个阶段表明颗粒之间的相对移动较小,土体位移对开挖面支护压力变化不敏感。另一方面,向洞内方向移动了较小的位移却引起了较大的应力变化。其原因主要是:在位移量较小时,盾构上前方土体具有明显的成拱效应,土拱以上部分的重力主要由开挖面两侧的颗粒承担,因而在支护压力减小很多时,土体的位移依然很小。从宏观力学角度,此阶段处在弹性向塑性转变的阶段。
当λ=0.20~0.12时,开挖面支护压力的变化幅度很小,而开挖面周围土体位移变化幅度很大,表现为开挖面周围土体对支护压力变化比较敏感。主要是因为这个阶段土拱效应发生变化,土拱效应逐渐减弱,土拱不断向地面移动,盾构开挖面上前方土体的滑移区域逐渐增加和扩张,滑移区域的土体在自重、摩擦力和开挖面的支护压力等因素的作用下形成暂时的稳定,这种稳定状态主要是依靠开挖面上方土体的移动而增加与周围土体产生摩擦效应下产生的,是被动调动土体摩擦效应的结果,因此需要产生较大的位移和变形才能形成的稳定状态。
当λ<0.12时,在支护压力不变的情况下,开挖面的土体位移不断加大。在这个阶段,开挖面前上方的土体形成明显的滑动面,滑移区域的土体在各种因素的作用下总体表现是失稳的,进入颗粒流动状态。
4.2 支护压力对地表沉降的影响
支护压力和地表沉降的关系如图7所示,通过该图可以看出在初始阶段,开挖面的支护压力对地面的沉降影响比较小;当λ=0.20~0.12区间时,地面沉降对支护压力反应较敏感;当λ=0.12时,开挖面已经失稳,但由于土拱作用,地面沉降相对不是很大,这也是砂卵石层地面滞后沉降的主要原因。
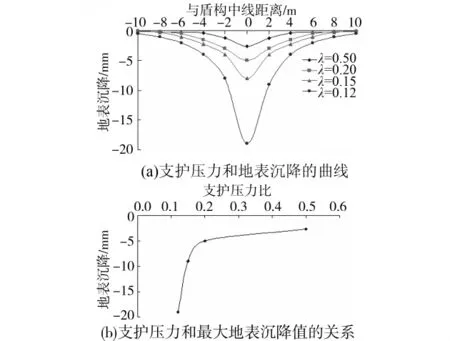
图7 支护压力和地表沉降的关系
Peck[20]提出地表沉降的预测方法被广泛应用于盾构施工中,其表达式为:

式中:Smax为盾构轴线处地面最大沉降量;i为地面沉降槽宽度系数,即沉降槽曲线拐点离盾构中线的水平距离。
众多学者对沉降槽宽度系数进行了研究,沉降槽宽度系数主要受地层条件、埋深和盾构直径的影响。韩煊等[21]通过对众多学者的研究结论进行对比分析,建议采用O'reilly等[22]的研究结论:

式中K称为沉降槽宽度参数,主要取决于土性。通常,对于无粘性土,约为0.2~0.3;对于硬粘土,约为0.4~0.5;而对于软粉质粘土,K可高达0.7。
李博等[23]对成都砂卵石地层盾构施工进行了地表沉降监测,通过对各断面实测曲线进行回归分析并找出曲线反弯点,得到K的取值范围在0.13~0.31之间,平均值为0.22。通过本算例计算可知,沉降槽宽度参数K为0.2,计算值和其实测值吻合良好。计算和实测均表明,砂卵石地层沉降影响范围小于粘土地层和软土地层。
4.3 开挖面变形分析
不同支护压力比的开挖面纵向和横向剖面变形如图8和图9所示。随着支护压力减小,开挖面扰动土体范围不断加大;扰动土体范围在水平方向的加大趋势不明显,而在重力方向扰动范围扩大趋势比较显著。

图8 不同支护压力比下的开挖面纵向剖面变形图
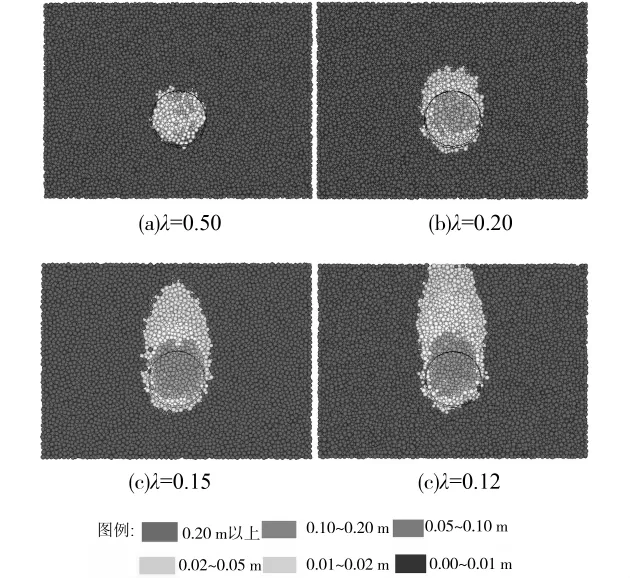
图9 不同支护压力比的开挖面横向剖面变形图
当λ=0.50时,开挖面前方土体已经被扰动并发生松动效应,松动范围为前方2m范围内的土体;松动的土体大致为椭圆形状,没有明显的下滑趋势和位移,颗粒位移主要为水平位移。
当λ=0.20~0.15时,松动范围继续加大,并向开挖面上方延伸,松动的土体形状由楔形体向仓筒状发展。
当λ=0.12时,开挖面已经失稳,开挖面前方土体已经进入流动状态,颗粒流动表现为仓筒形状,开挖面的土体位移与Kirsch[24]对干砂进行的模型试验结果基本相符,见图10。
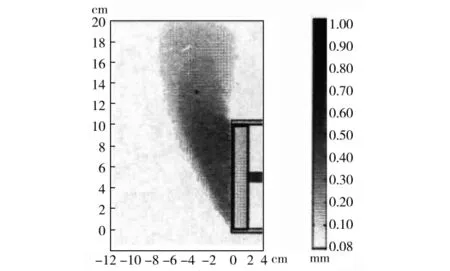
图10 开挖面破坏模式
4.4 开挖面土体应力的分析
图11 为不同支护压力比的接触力线图,从该图中可以看出,对于位移较小的土体,其接触力变化不大。当支护压力较小时,开挖面处土体发生较大的位移,由于卸载作用,接触力变得很小,该范围的土体已经发生明显的颗粒流动趋势。

图11 不同支护压力比的接触力线图
当λ=0.50~0.20时,开挖面的接触力逐渐发生变化;随着支护压力比值的减小,开挖面前方受扰动区域越来越大,松动区的形状由椭圆形向楔形体转变;随着支护压力比值减小,扰动区上部的宽度越来越大,并逐渐向开挖面的正上方发展。
当λ=0.15时,开挖面已经局部失稳,失稳的形状在开挖面前方为楔形体,开挖面上方为气泡状。
当λ=0.12时,开挖面失稳的范围继续扩大,开挖面上方基本为仓筒形状,随之地面也发生较大沉降。
通过接触线力图可以看出,在位移大于0.1m范围内的土体接触力较小,因此可以认为该区域已经失稳。失稳区域土体孔隙率上升,密度下降,力学性质也大大减低。因而,在盾构掘进过程中,土方超挖已经不可避免,在这种情况下如不及时增加支护压力,盾构掘进过后将在盾构上方形成较大空洞。
开挖面上方位移小于0.05m的土体颗粒,由于重力作用向下移动形成土拱。由于土拱作用,即使超挖出土形成土层内部空洞,也不会立刻引起地面塌陷,这是目前成都盾构施工引发地面滞后沉降的最主要原因。由于时间效应、土体弱化和外界荷载,盾构上方形成的空洞会缓慢发展到地面。
4.5 开挖面破坏模式分析
开挖面的失稳破坏模式是研究热点。Leca等[25]、魏纲[26]均提出了不同的开挖面失稳破坏模式。Chambon等[4]对均质砂土层进行了离心试验研究,图12(a)为其试验给出的不同埋深情况下开挖面的破坏形式。图12(b)为Kamata等[27]通过离心试验得到的不同支护压力下的破坏模式。
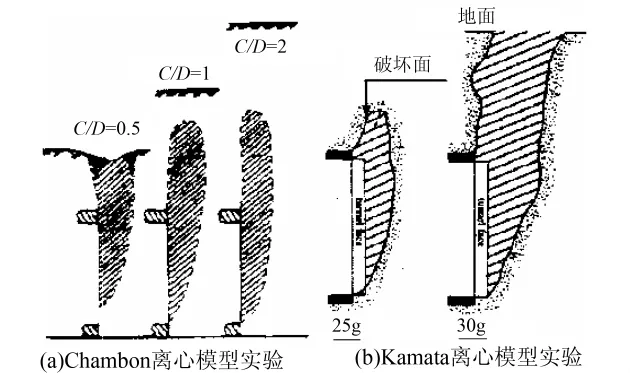
图12 砂土开挖面破坏模式
从上述试验可以看出以下规律:1)破坏面形状在开挖面前方大致为楔形体,开挖面上方基本为筒仓状;2)随着支护应力的变化,开挖面的破坏模式是变化的;3)随着埋深加大,破坏面反应不到地表。
通过前面对开挖面变形和应力分析可知,随着支护压力比值减小,开挖面土体破坏模式是变化的,经历了从椭圆形—楔形体—仓筒状的3个阶段,当支护应力比λ<0.12时,开挖面前方土体已经进入流动状态,颗粒流动表现为仓筒形状,数值模拟结果与 Chambon等[4]、Kirsch[24]和 Kamata等[27]离心模型试验结果相一致。
5 结 语
1)在松散卵石地层中,当支护力比值λ=1.00~0.20,开挖面位移相对较小;当λ=0.20~0.12时,开挖面位移变化幅度较大;当λ<0.12时,开挖面已经不能稳定,进入塑性流动状态。
2)盾构在砂卵石地层施工,对地面沉降影响范围小于粘土和软土地层,计算结果和实测吻合,沉降槽宽度参数K取0.2比较符合实际情况。
3)从接触力线图可以看出,开挖面前方土体扰动非常严重,当土体颗粒位移大于0.1m时,颗粒之间的接触力极低,颗粒流动的趋势强。
4)开挖面上方的土体由于颗粒移动调整而形成土拱,由于土拱作用,即使超挖出土而形成土层内部空洞,也不会立刻引起地面塌陷失稳,这是目前成都盾构施工引发地面滞后沉降的最主要原因。
5)随着支护压力比减小,开挖面土体破坏模式经历了从椭圆形—楔形体—仓筒状的3个阶段。
6)通过开挖面土体位移和接触线力分析可知,开挖面失稳后,开挖面前方土体破坏形状为楔形体,开挖面上方表现为仓筒状,这和砂土的离心试验模拟结果相符。
[1]刘建航,侯学渊.盾构法隧道[M].北京:中国铁道出版社,1991.
[2]韦良文,张庆贺,孙统立,等.盾构隧道开挖面稳定研究进展[J].重庆交通大学学报,2007,26(6):67-71.WEI Liangwen,ZHANG Qinghe,SUN Tongli,et al.Current research state of face stability in shield tunnelling and future development [J].Journal of Chongqing Jiaotong University,2007,26(6):67-71.
[3]张凤样,朱合华,博德明.盾构隧道[M].北京:人民交通出版社,2004.
[4]Chambon P,Corte J F.Shallow tunnel in cohesionless soil:stability of tunnel face [J].Journal of Geotechnical Engineering,1994,120(7):1148-1165.
[5]Mair R J,Taylor R N.Bored tunneling in the urban environment [C]//Proceedings of the Fourteenth International Conference on Soil Mechanics and Foundation Engineering,Hamburg,1997:2353-2385.
[6]程展林,吴忠明,徐言勇.砂基中泥浆盾构法隧道施工开挖面稳定性试验研究[J].长江科学院院报,2001,18(5):53-55.CHEN Zhanlin, WU Zhongming, XU Yanyong.Experimental study on stability of tunnel excavation surface in sand foundation by slurry shield method[J].Journal of Yangtze River Scientific Research Institute 2001,18(5):53-55.
[7]秦建设,尤爱菊.盾构隧道开挖面稳定数值模拟研究[J].矿山压力与顶板管理,2005,27(1):27-30.QIN Jianshe,YOU Aiju.Study on the face stability of shield tunnel in sand with numerical simulating technique[J].Ground Pressure and Strata Control,2005,27(1):27-30.
[8]黄正荣,朱伟,梁精华,等.浅埋砂土中盾构法隧道开挖面极限支护压力及稳定研究[J].岩土工程学报,2006,28(11):2005-2009.HUANG Zhengrong,ZHU Wei,LIANG Jinghua,et al.Study on limit supporting pressure and stabilization of excavation face for shallow shield tunnels in sand[J].Chinese Journal of Geotechnical Engineering,2006,28(11):2005-2009.
[9]乔金丽,张义同,高健,等.强度折减法在盾构隧道开挖面稳定分析中的应用[J].天津大学学报,2010,43(1):14-20.QIAO Jinli,ZHANG Yitong,GAO Jian,et al.Application of strength reduction method to stability analysis of shield tunnel Face[J].Journal of Tianjin University,2010,43(1):14-20.
[10] Karim A M.Three-dimensional discrete element modeling of tunneling in sand [D].Edmonton:University of Alberta,2007.
[11]王明年,魏龙海,刘大刚.卵石地层中地下铁道施工力学的颗粒离散元法模拟技术及应用[M].成都:西南交通大学出版社,2010.
[12]王明年,魏龙海,路军,等.成都地铁卵石层中盾构施工开挖面稳定性研究[J].岩土力学,2011,32(1):99-105.WANG Mingnian,WEI Longhai,LU Jun,et al.Study of face stability of cobble-soil shield tunneling at Chengdu metro[J].Rock and Soil Mechanics,2011,32(1):99-105.
[13]郭庆国.粗粒土的工程特性及应用[M].郑州:黄河水利出版社,1998.
[14]Itasca Consulting Group Inc.PFC3D(particle flow code in 3dimensions)theory and background [R].Minnesota,USA:Itasca Consulting Group Inc,2002.
[15]Cundall P A.A computer model for simulating progressive:large scale movement in blocky rock systems[C]//Proceedings of the Symposium of the International Society for Rock Mechanics, Nancy,France,1971:129-136.
[16]孙其诚,王光谦.颗粒物质力学导论[M].北京:科学出版社,2009.
[17]周健,池永.砂土力学性质的细观模拟[J].岩土力学,2003,24(6):901-906.ZHOU Jian,CHI Yong.Mesomechanical simulation of sand mechanical properties [J].Rock and Soil Mechanics,2003,24(6):901-906.
[18]Martin P J,Steffen A,Conrad C.The impact of porosity and crack density on the elasticity,strength and friction of cohesive granular materials:insights from DEM modeling[J]International Journal of Rock Mechanics & Mining Sciences,2009(46):250-256.
[19]Belheine N,Plassiard J P,Donze F V,et al.Numerical simulation of drained triaxial test using 3Ddiscrete element modeling [J].Computers and Geotechnics,2009,36:320-331.
[20]Peck R B.Deep excavations and tunneling in soft ground[C].//Proceedings of 7th International Conference on Soil Mechanics and Foundation Engineering,Mexico,1969:275-290.
[21]韩煊,罗文林,李宁.地铁隧道施工引起沉降槽宽度的影响因素[J].地下空间与工程学报,2009,5(6):1188-1193.HAN Xuan,LUO Wenlin,LI Ning.The width of settlement trough influenced by tunneling in soft ground[J].2009,5(6):1188-1193.
[22]O'reilly M P,New B M.Settlements above tunnels in the United Kingdom-their magnitude and prediction[C]//Proceedings of Tunnelling'82Institution of Mining and Metallurgy,London,1982:173-182.
[23]李博,苏华友,赵旭伟.成都地铁盾构隧道地表沉降分析[J].城市轨道交通研究,2010,1(4):64-66.LI Bo,SU Huayou,ZHAO Xuwei.Analysis on metro ground settlement caused by shield tunneling in chengdu city[J].Urban Mass Transit,2010,1(4):64-66.
[24]Kirsch A.Experimental investigation of the face stability of shallow tunnels in sand [J].Acta Geotechnica,2010(5):43-62.
[25]Leca E,Dormieux L.Upper an lower bound so1utions for the face stability of shallow circular tunnels in frictional material[J].Geotechnique,1990,40(4):581-606.
[26]魏纲.顶管工程土与结构的性状及理论研究[D].杭州:浙江大学,2005.
[27]Kamata H,Masimo H.Centrifuge model test of tunnel face reinforcement by bolting [J].Tunneling and Underground Space Technology,2003,18(2):205-212.
