基于零空间表示和最大似然的欠定盲源分离方法

王荣杰，詹宜巨，周海峰

(1.中山大学 信息科学与技术学院，广东 广州 510006；2.中山大学 工学院，广东 广州 510006；3.集美大学 轮机工程学院，福建 厦门 361021)

1 引言

近年来，鉴于盲源分离优越的假设前提，其模型被广泛用于数字通信、语音、图像处理、船舶工程、机器人导航和生物医学信号处理等领域[1～6]。所谓的盲源分离，就是在源信号和混合系统(或传输通道)等未知的情况下，仅根据源信号的统计特性，由观测到的混叠信号恢复出源信号。根据观测信号和源信号的个数，盲源分离可分为超(正)定盲源分离和欠定盲源分离。超正定盲源分离有很多成熟的方法，如 ICA独立分量分析[7,8]、修正的Stone法[9]、阶统计代数法[10]等。但这些方法不适用于观测信号的个数少于源信号的个数的情况，欠定盲源分离(UBSS, underdetermined blind source separation)是本文的研究重点。传统的欠定盲源分离算法主要可分为2类：一类是利用源信号的稀疏性来处理，文献[11]提出利用聚类技术和最小化 l1范数相结合的方法来恢复时域稀疏的源信号，文献[12,13]提出利用时频变换方法将非稀疏信号变换到时频域，以达稀疏的目的，它们认为在每个时频区域内只有一个源信号不为零；这些方法都选择服从超高斯分布的语音为源信号。另一类是利用广义分布模型作为源信号的概率密度的贝叶斯估计法[14,15]，这类方法的主要缺点是计算复杂，在一定程度上降低了源信号的恢复质量。这些传统的算法都假设源数为已知。本文提出一种源数未知的欠定情况下任意分布源信号的盲分离方法，该方法首先利用S变换和聚类技术相结合来估算源数和混叠矩阵，然后将源信号以零空间形式表示，最后通过最大似然 (ML,maxima likelihood) 法估计关于它的后验概率以达到恢复源信号的目的。

2 问题的描述

假设n个彼此相互独立的未知源信号s(t)=[s1(t),s2(t), …, sn(t)]T，通过一未知瞬时线性混合系统后，得到m个观测信号x(t)=[x1(t), x2(t), …, xm(t)]T。观测信号x(t)与源信号s(t)的关系可由式(1)表示。

其中，A∈Rm×n为混合矩阵，它反映了混合系统或信道的传输特性，要求它为行满秩，t=0, … ,N-1为时域采样点。为了便于分析，在推导过程中将s(t)和x(t)分别记为s和x。

在m ≥ n的情况下，给定A，源信号s可由式(2)估计得到。

其中，A*为A的广义逆矩阵，A*= AT(AAT)。

当m＜ n时，即为欠定情况，既便A已知，对于源信号s的恢复也不是唯一，只能通过估计方法估计出s的最优估计值。

3 源数和混叠矩阵的估计

在第4节中分析的前提条件是假设混叠矩阵A和n为已知，特别在传统算法中的n都设为已知，但在实际中A和n都是未知的。本文采用了一种基于S变换的单源测试(SSD, single source detention)方法，首先以此为准则选择出时频域的单源观测信号，然后采用聚类技术分别估计源信号个数n和混叠矩阵A。

3.1 基于S变换的单源测试方法

S变换是Stockwell于1996年提出的一种可逆的局部时频分析方法，其思想是对连续小波变换和短时傅里叶变换的发展。它不同于短时傅里叶变换之处在于采用的高斯窗口的高度和宽度随频率而变化，这样就克服了短时傅里叶变换窗口高度和宽度固定的缺陷[16,17]。观测信号的 S变换可由式(3)和式(4)计算得到。

式(3)和式(4)中，i=1,…,m，代表时间的 t =0, …,N-1，代表频率的k=0, …, N-1；式(4)中的(·)为式(3)中信号的傅里叶变换。

表1 不同单源信号测试方法计算复杂度的比较

式(5)中，║·║，Re[·]和 Im[·]分别为 Frobenius 范数，取实部和取虚部运算。如果时频点(t, k)为单源点时，且存在(t, k) ≠ 0(i=1, …, m)，那么 XS(t, k)中所有的元素均由某一个相同的源信号与混合矩阵 A中的元素相乘获得，因此为纯实数向量，即；如果(t, k)不为单源点时，那么为复数向量，而不为零且为一正数。式(5)中的ε为一个正数。由于具有单源特性的观测信号XS(t,k)的实部或虚部与对应的A中的列向量之间具有相同的绝对方向[19]，因此本文利用与传统的基于稀疏特性的欠定混合矩阵估计算法中的聚类技术对具有单源特性的观测信号进行聚类估计混合矩阵，同时源信号的个数也可利用单源信号的特性和聚类技术来估计；式(5)中的Ψs为具有单源特性观测信号XS(t,k)实部的集合。基于S变换的单源测试方法不仅克服了其他传统单源测试方法中的时频变换窗函数和长度重叠选择盲目性的缺陷；同时，与传统单源测试方法相比较，本文方法的计算简单，通过表1比较了3种不同单源测试方法的计算复杂度可以证明。

表1中时频变换的点数均设为N；利用表中的3种方法将每一个单源性观测信号变为用于估算混合矩阵的聚类元素项还需如下计算量：本文的方法只需 m次取实部运算；而文献[13]的方法需3m+2次乘法运算、3(m-1)次加法运算和 2m 次取实(虚)部运算；文献[19]的方法需m+1次乘法运算、(m-1)次加法运算和m次取实(虚)部运算。

3.2 源数和混叠矩阵的估计

由于源数是未知的，并且欠定情况下的源数也不能用PCA或SVD进行估算。为了估算源信号的个数，本节采用一种基于聚类验证技术确定源数，该方法根据不同的聚类数(聚类数c=2,…, cmax)对式(5)中的单源性元素进行模糊 c均值聚类(fuzzy c-means clustering)，并以式(6)为准则对不同c的聚类结果进行评估得到最优聚类数，即为源数。

式(6)中的 Scat(c)和 Sep(c)不仅与聚类数 c有关，还与单源观测信号集合 Ψs中的元素和聚类中心相关，它的具体计算可参考文献[20]。Scat(c)表示聚类数为c的聚类紧凑性，当聚类紧凑性越好时Scat(c)的值将越小，它的值在0～1之间；Sep(c)用于描述聚类数为c时聚类中心分布情况，称为聚类分离度；当聚类中心分布越合理时，它的值也将越小。因此，最小化式(6)，便可获得 Ψs的最佳聚类数，即确定源信号个数。当源数确定后，混叠矩阵将根据最优聚类下的元素来估算。设ai为A的第i列向量，具体由式(7)估算得到。

4 源信号的恢复

在A和n都已知的欠定情况下，盲源分离算法就是要从x得到s的最优估计。本节在假设A和n已知情况下，首先介绍了源信号的零空间表示[21]，在此基础上采用了一种基于ML估计的方法来恢复源信号。

4.1 源信号的零空间表示

为了便于分析，先设式(1)中的A由一个m阶的对角阵Λ和m×(n-m)维的0矩阵组成，记Λ=diag[λ1, …, λm]且 λi＜ λi-1, λi( i=1, … ,m)＞0，那么式(1)可改写成式(8)。

由式(8)可知，s的前m个值可由式(9)得到。

其余的(n-m)个s用一个(n-m)维列向量的r表示，r =[r1,…, rn-m]T。由此式(8)中s的解可用式(10)来描述。

当混合矩阵A不满足式(8)中的特殊形式时，它的s解也就不能直接用式(10)来描述。但由于A为行满秩，它的SVD奇异值分解中含m个不为零的特征值，可写成A=U(Λ, 0)V，将其代入式(1)，并根据式(10)，可得到s的解如式(11)所示。

由式(12)可知，当 A已知，那么估计了(n-m)个的r就相当于估计n个的s。

4.2 源信号的恢复

为了能同时分离服从任意分布的源信号，本文选取具有对称单峰分布特性的广义高斯模型 (GGM,generalized Gaussian model)[18,22]作为源信号的概率密度，式(13)为它的通用数学表达式。

其中，α为信号z的方差，()Γ·为Gamma函数；调节β的值可得出不同的分布函数模型，β=2表示标准高斯分布，β＜2时为超高斯分布，β＞2时为亚高斯分布。

设 X=[ x(0), …, x(N-1)]，R=[r(0), … ,r(N-1)]，S=[ s(0), …, s(N-1)]，q=[α1, …, αn, β1, …,βn]T，并记S的概率密度为f(S|q)。那么可得X和R的联合分布函数如式(14)所示。

为了估计每个源信号分布函数模型中的α和β，构造关于参数向量q的先验似然函数如式(15)所示。

由最大似然估计法可知

即

式(14)～式(17)中，由于A独于立于q，且分布p(X|A,q)和 p(A)是非负的，因此 q的最大似然估计可简化为式(18)。

式(18)中估计出q后，根据关于R的后验概率P(R | X q; A)利用Metropolis-Hastings算法[23]将产生R的抽样序列(k=K0, …, K; K0＞0为burn in周期)。基于这抽样序列，可定义关于后验概率均值的二次型损失期望函数如式(19)所示。

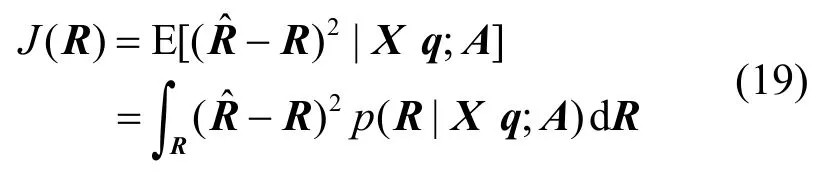
最小化式(19)中的 J(R)可得到后验概率均值的估计值，它可由式(20)抽样序列的经验均值来逼近。

从上述的分析过程可知，由式(18)和式(20)结合可估计出r(t)，然后将其代入式(12)中就可以得到s(t)的估计值。

5 仿真实验分析

本文提出的源数未知的欠定盲源分离算法实现步骤如下。

step 1 源数n和混叠矩阵A的估计

1) 由式(3)和式(4)对 X进行 S变换，得到XS(t,k)，t=0,…,N-1, k=0,…,N-1;

2) 由式(5)选择XS(t,k)中具有单源性的信号，得到Ψs；

3) 利用文献[20]中的FCM对Ψs进行c(c=2,…,cmax)聚类，并由式(6)确定n；

4) 由式(7)估算混叠矩阵A；

step 2 源信号s的恢复

1) 利用最大似然法估计式(18)中的参数向量q;

2) 利用文献[23]中的 Metropolis-Hastings算法和式(20)相结合估算r；

3) 将step 1中的A和r代入式(12)，即可得到s的估计值。

在仿真验证实验中选取的源信号时域波形如图1所示，本文的仿真平台为MATLAB R2010b。

为了更好地检验基于S变换和聚类验证技术相结合的源数估计法，利用例1、例2和例3这3个例子加以验证。例1的源信号选{s1, s3}，例2的源信号选{s1, s2, s3}，例3的源信号选{s1,s2, s3, s4}，在这3个例子的仿真实验中A都是在[-1 1]之间随机产生的，且 m=3。它们的仿真结果如图2所示。由图2可知，聚类数越接近于最优值时它的聚类验证指数越小，由式(6)可以准确地确定例 1、例 2和例 3的源数；由此可表明基于S变换和聚类验证技术相结合的估计法不仅能准确估计欠定情况下的源数，也适用于超定情况。

图1 源信号

图2 聚类验证指数曲线

为了全面验证本文提出的UBSS方法的有效性，还将该方法与其他文献的方法进行比较加以验证。在这个仿真实验中，式(1)中的 A同样也是在[-1 1]之间随机产生的，它的值见式(21)，本文欠定混合矩阵估计方法与文献[13]、文献[16]、文献[19]等不同方法估计的结果如表 2所示。利用本文、文献[13]和文献[24]等 3种不同UBSS方法实现的分离信号如图3所示；源信号估计方法的性能由式(22)评价，利用它对源信号估计性能的比较如表3所示。

表2 不同混合矩阵估计方法的估计结果的比较

表3 不同UBSS方法分离结果的比较

由表2和表3的比较结果，以及图3的波形可知，本文的欠定盲源分离方法不仅能较好地分离出超高斯和亚高斯2种不同分布的信号，同时它在A和源信号恢复的性能上也体现了它比其他方法更具有优越性。另外，在仿真实验中，由式(18)得到源信号(s1,s2,s3,s4)分布函数中的 α的估计值分别为1.059 3，1.010 7，0.091 0，0.083 5；β的估计值分别 70.010 9，172.850 5，0.795 7，1.888 7，由 β 的值可知s1, s2为亚高斯分布信号，s3, s4为超高斯分布信号；为验证这一结论，直接计算源信号的峭度，(s1,s2,s3,s4)的峭度分别为1.500 1，1.500 0，6.417 0，5.830 0，当峭度大于3的信号为超高斯分布，小于3的信号为亚高斯分布，由此说明上述结论是正确的。

图4 不同源信号估计算法的恢复信号

为了进一步评价第3节提出的源信号估计算法的性能，分别利用该算法与文献[14,15]的算法分离出欠定情况下的EEG(脑电图)信号进行比较分析，3种源信号恢复算法的复杂度运算量为：本文的算法需估计2n个参数，2n次最大化运算，1次Metropolis-Hastings抽样运算；文献[14]的算法需要估计2n个参数，6n次最大化运算，6n次Metropolis-Hastings抽样运算；文献[15]的算法需要估计2nL个参数，2nL次最大化运算，L次Metropolis-Hastings抽样运算，L为该算法的收敛迭代步长。图 4(a)中的源信号s1和s2为服从超高斯分布的EEG信号，而s3为服从亚高斯分布的噪声信号，它们都取自文献[25]；而混叠矩阵A的值见式(25)，它也是在[-1 1]之间随机产生，m=2。在这个仿真实验中，假设混合矩阵A和源数n均为已知，图4(b)为观测信号，图4(c)～图 4(e)分别为 3种不同源信号估计算法的分离信号，它们对源信号估计的性能比较如表4所示。

表4 不同源信号估计算法实验结果的比较

由图4和表4的比较结果可知，虽然文献[15]中概率分布函数对信号建模具有较高的自由度，但大量参数的估计不仅使得该算法的计算复杂，且源信号恢复性能差；利用本文的算法恢复的源信号s1和s2的β估计值分别为1.116 8和1.559 1；与文献[14,15]的算法比较，该算法具有计算简单和估计性能优越等特点。

6 结束语

针对欠定情况下的源数估计、混叠矩阵和源信号恢复等关键技术，本文提出了一种源数未知的欠定盲源分离算法。该方法首先利用S变换和聚类技术相结合的方法来估算源数和混叠矩阵；然后将源信号以零空间形式表示，这种表示形式将求解n个未知数的问题变换成求解(n-m)个的未知，再通过最大似然法估计关于它的后验概率以达到恢复源信号的目的。仿真结果表明了该方法不仅能较好地分离出服从不同分布的源信号，同时它比其他方法具有更好的估计性能。本文提出的源信号个数和混合矩阵的估计是利用聚类技术对 SSD的元素进行聚类获得的，而SSD元素的选取依据是实数的观测信号在S变换时频域上满足提出的SSD条件；在源信号恢复方面，通过最大似然法估计关于它的后验概率只适用于恢复混合矩阵为实数矩阵情况下的源信号，但源信号的零空间表示法也适用于混合矩阵为复数矩阵情况，这为复数混合矩阵的欠定盲源分离方法的研究提供了重要的思路，同时复数混合矩阵的欠定盲源分离方法的研究将成为我们下一个研究目标。

[1] LIU Y D, ZHOU Z T, HU D W. A novel method for spatio-temporal pattern analysis of brain fMRI data[J]. Science in China Series F, Information Sciences, 2005, 48(2): 151-160.

[2] ARAKI S, MAKINO S, BLIN A. Underdetermined blind separation for speech in real environment with sparseness and ICA[A]. Processings of ICASSP ’04[C]. Montreal, Canada, 2004. 881-884.

[3] 王荣杰, 周海峰, 詹宜巨. 船舶噪声的自适应分离技术[J]. 中国航海, 2011, 34(3): 10-15.WANG R J, ZHOU H F, ZHAN Y J. Adaptive separation technology of ship noise[J]. Navigation of China, 2011, 34(3): 10-15.

[4] OHNISHI N Y, IMIYA A. Independent component analysis of optical flow for robot navigation[J]. Neurocomputing, 2008, 171(10-12):2140-2163.

[5] ANNA T, LUIGI B, EMANUELE S. A markov model for blind image separation by a mean-field EM algorithm[J]. IEEE Transactions on Image Processing, 2006, 15(2): 473-482.

[6] BAI E W, LI Q Y, ZHANG Z Y. Blind source separation/channel equalization of nonlinear channels with binary inputs[J]. IEEE Transactions on Signal Processing, 2005, 53(7): 2315-2323.

[7] CICHOCKI A, AMARI S. Adaptive Blind Signal and Image Processing[M]. New York: Wiley, 2002.

[8] DOUGLAS S C, GUPTA M, SAWADA H. Spatio-temporal fastICA algorithms for the blind separation of convolutive mixtures[J]. IEEE Trans Audio, Speech, Lang Process, 2007, 15(5): 1540-1550.

[9] XIE S L, HE Z S, FU Y L. A note on stone’s conjecture of blind separation[J]. Neural Computation, 2005, 117(2): 321-330.

[10] EVEN J, MOISAN E. Blind source separation using order statistics[J].Signal Processing, 2005, 85(9): 1744-1758.

[11] FANG Y, ZHANG Y. A robust clustering algorithm for underdetermined blind separation of sparse sources[J]. Journal of Shanghai University(English Edition), 2008, 12(3): 228-234.

[12] BOFILL P, ZIBULEVSKY M. Underdetermined source separation using sparse representation[J]. Signal Process, 2001, 81(11):2353-2362.

[13] ABDELDJALIL A, NGUYEN L, KARIM A. Underdetermined blind separation of nondisjoint sources in the time-frequency do-main[J]. IEEE Transactions on Signal Processing, 2007, 55(3):897-907.

[14] CEMGIL A T, FEVOTTE C, GODSIIL S J. Variational and stochastic inference for bayesian source separation[J]. Digital Signal Processing,2007, 17(5): 891-913.

[15] SNOUSSI H C, IDIER J. Bayesian blind separation of generalized hyperbolic processes in noisy and underdeterminate mixtures[J]. IEEE Transactions on Signal Processing, 2006, 54(9): 3257-3269.

[16] WANG R J, ZHAN Y J. Application of similarity in fault diagnosis of power electronics circuits[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2010, E93-A(6):1190-1195.

[17] STOCKWELL R G, MANSINA L, LOWER R P. Localization of the complex spectrum: the s transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001.

[18] KIM S Y, CHANG D Y. Underdetermined blind source separation based on subspace representation[J]. IEEE Transactions on Signal Processing, 2009, 57(7): 2604-2614.

[19] REJU V G, KOH S N, SOON I Y. An algorithm for mixing matrix estimation in instantaneous blind source separation[J]. Signal Processing, 2009, 89(9): 1762-1773.

[20] SUN H J, WNNG S R, JIANG Q S. FCM-based model selection algorithms for determining the number of cluster[J]. Pattern Recognition, 2004, 37(10): 2027-2037.

[21] CHEN R B, WU Y N. A null sapce method for over-complete blind source separateion[J]. Computational Statistics & Data Analysis, 2007,51(12): 5519-5536.

[22] 史习智. 盲信号处理[M]. 上海：上海交通大学出版社,2006.SHI X Z. Blind Signal Processing[M]. Shanghai: Shanghai Jiaotong University Press, 2006.

[23] ROBERT C, CASELLA G. Monte Carlo Statistical Methods[M].New York: Springer-verlag, 1999.

[24] KHOR L C. Robust adaptive blind signal estimation algorithm for underdetermined mixture[J]. IEE Proceedings-Circuits, Devices and Systems, 2006, 153(4): 320-331.

[25] CICHOCKI A, AMARI S, SIWEK K. ICALAB toolboxes [EB/OL].http://www.bsp.brain.riken.jp/ICALAB/ICALABSignalProc/benchmar ks, 2007.