多径衰落信道中扩频信号处理增益的上限

马万治，王俊，唐友喜

（电子科技大学 通信抗干扰技术国家级重点实验室，四川 成都 611731）

1 引言

随着无线通信技术的发展，扩频信号在无线通信领域得到了广泛的应用。一方面，扩频信号是无线通信常见时间同步及频率同步的基本信号形态；另一方面，扩频信号是无线通信系统常用抗干扰、低截获特性的承载体。参考文献[1]中，扩频增益定义为信号扩展频谱后的带宽与原信号带宽之比；处理增益定义为接收机输出信噪比与输入信噪比之比。与扩频增益相比，处理增益更能直观地反映扩频机制对通信性能的影响。因此，讨论多径衰落信道中扩频信号的处理增益是有意义的。

加性白高斯噪声信道(AWGN)中，扩频信号的处理增益等效于扩频增益[1,2]，当扩频码片数无限增加时，扩频增益无限增大，扩频信号实际获得的处理增益也会无限增大。考虑信号带宽是原始符号扩频后的信号总带宽，符号长度是原始符号扩频后的总持续时间，若给定符号长度，扩频码片数无限增加等价于信号带宽无限增大；若给定信号带宽，扩频码片数无限增加等价于符号长度无限增大。由此，当信号带宽无限增大或符号长度无限增大时，扩频信号的处理增益会无限增大，即处理增益不存在上限。针对AWGN信道中的直接序列扩频系统，给定信号带宽与比特速率，文献[3]分析了存在单音或宽带干扰时，二进制相移键控(BPSK)、正交相移键控(QPSK)以及16值正交幅移键控(16QASK)调制信号的扩频增益与误比特率，其中，16QASK处理增益最大，QPSK误比特率最低。

到目前为止，对于多径衰落信道中扩频信号的处理增益，业界已有了一些研究。针对不同的扩频因子，文献[4]仿真了多径信道中二维扩频信号经过信道均衡后的误码率性能，随着扩频因子的增大，误码率不会一直降低。针对直接序列扩频与快速跳频混合的码分多址信号(DS/FHHCDMA)，给定信号功率与带宽并且采用最大比合并，以最大化频谱利用率为准则，文献[5]研究了多径衰落信道中直序扩频的最优处理增益，随着信噪比的提高、用户数的减少以及跳频点数的增加，直序扩频的最优处理增益会降低。考虑多径衰落信道中的时频二维扩频系统，针对导引辅助的相干检测，文献[6]说明在一个扩频符号所占用的信号时频二维区域等于信道的时频相干区域时，扩频信号的处理增益取得最大值。然而，对于非相干检测时扩频信号处理增益的最大值，至今未见有文献报道。

本文针对联合相干非相干检测算法，给出多径衰落信道中扩频信号处理增益与信号带宽、符号长度的关系表达式，并分析信号带宽无限增大或符号长度无限增大时，扩频信号处理增益的变化趋势，寻找扩频信号处理增益的上限。本文的其余部分安排如下：第2节给出系统模型，第3节分析处理增益与信号带宽、符号长度的相互关系，第4节中给出数值与仿真结果，第5节为结束语。

2 系统模型

为了方便分别改变信号带宽与符号长度，本文采用时频二维扩频的系统模型[4]，如图1所示。发射机分别对BPSK调制导引符号 bP、数据符号 bD进行时频二维扩频，其中，bP取值+1、bD取值±1；将导引扩频输出 XP与数据扩频输出 XD合并得到X；经正交多载波调制，产生发射信号 s（t）。发射信号经过充分散射的多径衰落信道到达接收机。接收机对接收信号 r（t）进行正交多载波解调，产生时频二维矩阵R；经联合相干非相干检测，得到数据符号的估计值。

2.1 发射机

导引符号 bP经过时频二维扩频[4]后，得到M行N列的导引扩频输出矩阵 XP。如式(1)所示，为XP中的第m行第n列元素；为导引扩频矩阵第m行第n列元素；M表示频域子载波个数，N表示时域码片个数。数据符号 bD的与导引符号 bP的时频二维扩频过程类似，这里不再赘述。

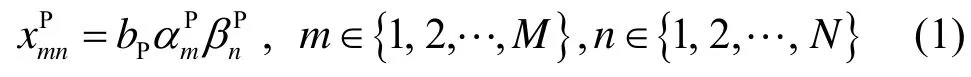
按照块状导引插入方式，将导引与数据扩频输出合并[7]。其具体内容：在数据矩阵 XD的相邻2列码片之间插入1列导引码片。导引插入后得到M行2N列时频二维矩阵X。然后经过正交多载波调制，X变换为时域数据 s（t）。如式(2)所示， Tw表示一个时域码片的持续时间， xmn为X中第m行第n列元素。s(t)经过添加循环前缀及射频处理后，馈入天线。

图1 系统模型(iifτ、分别表示充分散射多径衰落信道第i条径的多径延时与多普勒频移)

2.2 信道

考虑充分散射的多径衰落信道，即散射体密集分布在发射端和接收端的各个方向上，接收信号由时间和空间上连续到达的多径分量组成[8]。针对本文讨论的时频二维扩频信号，其信号带宽在零到无穷大内变化，取值范围很广。当信号带宽无限增大时，宽带信号接收机的时间分辨率远小于多径最大时延，此时，以时间分辨率为间隔，连续的多径分量可分割为多条可分辨径[9]。因此，发射信号 s（t）经过充分散射的多径衰落信道得到接收信号 r（t）：

其中，τi为第i条径的时延，取值iBs；hi为第i条径的衰落因子，服从瑞利分布，且不同路径的 hi相互独立； n（t）为叠加在信号上的加性白高斯噪声。本文假设信道多径延时分布为负指数分布[9,10]，即，其中，tm= 5 × 1 0-6为负指数分布的衰落因子。

多径信道中，若存在多普勒扩展，则信道的时间选择性衰落受最大多普勒频移fd影响，用相干时间Tc表征[11]。

多径信道的频率选择性衰落，受多径延时分布影响，用相干带宽 Bc表征[11]。给定信道的相干带宽Bc由式(5)、式(6)确定[12]，其中，为高斯超几何函数。

当Bs取值无限大时，接收机的时间分辨率无限小，多径衰落信道中的可分辨径无限多，结合服从负指数分布的信道多径延时分布模型，式(5)变形为积分形式：

联合式(6)、式(7)求解得到Bs取值无限大时的信道相干带宽：

2.3 接收机

假设收发双方已完成精确的时频同步，接收机经过射频处理并且去除循环前缀，得到接收信号r（t）。r（t）经过DFT变换，实现了正交多载波解调，得到了时频二维接收矩阵R。

假设接收信号中各个子载波的输入信号功率均为 Psi，输入噪声功率均为 Pni，则接收机的输入信噪比为 PsiPni。接收矩阵R中的元素如式(10)、式(11)所示。其中，为第m行第n列导引和数据码片的信道衰落因子；为叠加在第m行第n列导引和数据码片上的加性白高斯噪声；为 XD中第m行第n列元素，为 XP中第m行第n列元素。

经过正交多载波解调后，对接收矩阵R进行联合相干非相干检测。

1) 导引、数据恢复

分离导引、数据，得到导引矩阵 RP与数据矩阵RD。假设， RP与导引扩频矩阵的对应元素相乘得到H，RD与数据扩频矩阵的对应元素相乘得到S，如式(12)、式(13)所示。

2) 相干区域划分

给定信道相干带宽Bc与相干时间Tc，在接收矩阵R中，Bc除以子载波带宽后得到频域相干码片个数(即相干行数)、Tc除以时域码片持续时间(包含循环前缀)后得到时域相干码片个数(即相干列数)。设R的相干行数为B，相干列数为T，则：

其中，Bs为信号带宽，Ts为符号长度，η为非循环前缀部分的长度占总符号长度的比例，Bo为一个子载波的带宽，min表示取最小值，表示向下取整。

如式(16)所示，将R从上至下、从左至右顺序划分子矩阵，且每个子矩阵大小为B×T。子矩阵占据的时频二维空间由相干行数与相干列数限定，因此又称子矩阵为相干区域。结合式(14)～式（15），则R能够划分NBNT个相干区域：

3) 相干检测

不失一般性，假设信道响应在相干区域内完全一致，在相干区域之间统计独立。针对第x行第y列相干区域，分离出导引码片得到信道估计值；分离出数据码片得到数据估计值。在对数据估计值进行信道补偿后，相干区域内部的相干检测完成。

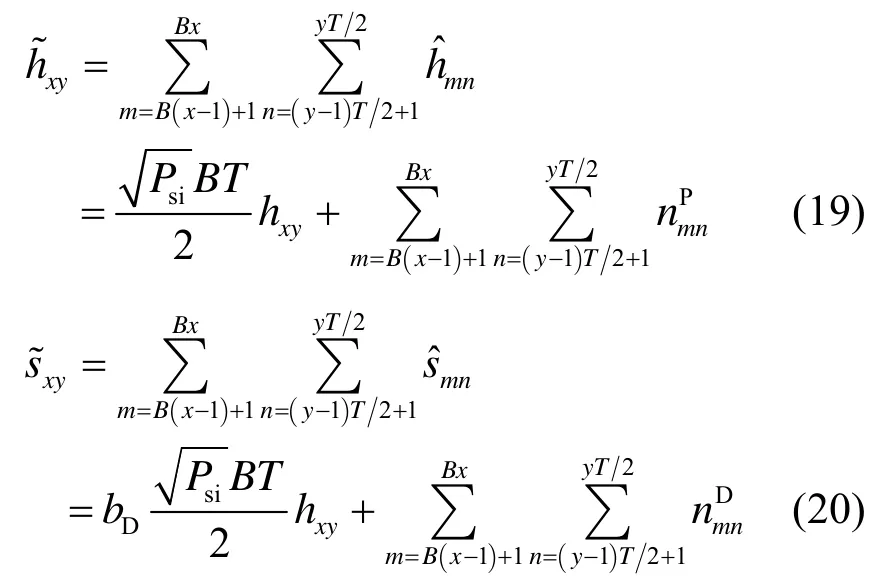
其中，x∈｛1,2,…,NB｝、y∈｛1,2,…,NT｝ ，表示导引矩阵中第m行第n列元素，表示数据矩阵中第m行第n列元素，hxy表示第x行第y列相干区域的真实信道响应。

4) 非相干检测

将所有相干区域的检测结果累加，实现非相干检测。由于相干区域之间的信道衰落是统计独立的，非相干检测能够增加接收的分集度。结合式(12)～式(13)、式(19)～式(20)，得到符号判决量。

式(21)中第1项为期望信号，第2项是输入噪声一次项的加权和，第3项是输入噪声二次项之和，其中，后2项共同构成判决变量中的噪声分量。为简化叙述，文章后续部分将第2项称为噪声一次项，第3项称为噪声二次项。最后，将判决变量送入解调模块，输出数据符号的估计值。

3 性能分析

3.1 处理增益分析

考虑充分散射多径衰落信道中时频二维扩频的BPSK调制信号，针对联合相干非相干检测算法，本节就其处理增益进行分析。扩频信号处理增益定义为接收机解扩输出信噪比与输入信噪比之比[2]如式(22)所示，其中，Pso为输出信号功率，Pno为输出噪声功率，Pso/Pno为输出信噪比。

由于信道衰落因子hmn为复高斯随机变量，其均值为零、方差为，且不同相干区域的hxy独立同分布，则服从自由度为2NBNT的χ2分布。假设=1，分别对式(21)中的期望信号分量与噪声分量求功率，得到输出信号功率与输出噪声功率，如式(23)、式(24)所示。

结合式(23)、式(24)，得到信号经过联合相干非相干检测后的输出信噪比：

扩频信号的处理增益：

当BTPsi/Pni＞＞1，即输入信噪比足够大时，式(24)中的噪声一次项决定了输出噪声功率的大小。从式(26)中容易看出，此时处理增益与相干区域的大小、个数近似成正比。当BTPsi/Pni＜＜1，即输入信噪比足够小时，式(24)中的噪声二次项决定了输出噪声功率的大小。从式(26)中容易看出，此时输出信噪比急剧下降，处理增益不仅受相干区域的大小、个数影响，还与输入信噪比成正比。

3.2 处理增益上限

针对联合相干非相干检测算法，式(2)给出了多径衰落信道中，BPSK调制时频二维扩频信号的处理增益表达式。为深入分析处理增益的变化趋势，现给出如下假设：

1) 相干时间能够映射为整数个时域相干码片，相干带宽能够映射为整数个频域相干码片；

2) 接收矩阵R能够划分为整数个相干区域；

3) 信噪比Eb/N0恒定，且Eb/N0=BsTs Psi/Pni。

在多径衰落信道中，信号参数与信道参数之间的关系决定了不同的发送信号将经历不同的衰落类型[11]。针对信道衰落的4种类型，分别对处理增益进行化简、分析。

① 平坦慢衰落

当Bs≤Bc且Ts≤Tc时，信道衰落为平坦慢衰落。此时，根据式(14)、式(15)，式(26)可化简为

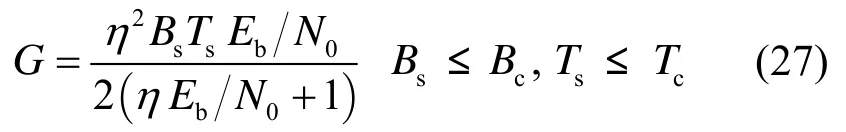
假设Eb/N0＞＞1，由式(27)可知，当信号带宽小于相干带宽，并且符号长度小于相干时间时，扩频信号的处理增益与信号带宽、符号长度成正比，即在信号的时频二维空间与信道相干区域一致时，扩频信号的处理增益取得最大值。这一结论与文献[6]的结论一致。

②频选慢衰落

当Bs＞Bc，Ts≤Tc时，信道衰落为频选慢衰落。

此时，根据式(14)、式(15)，式(26)可化简为

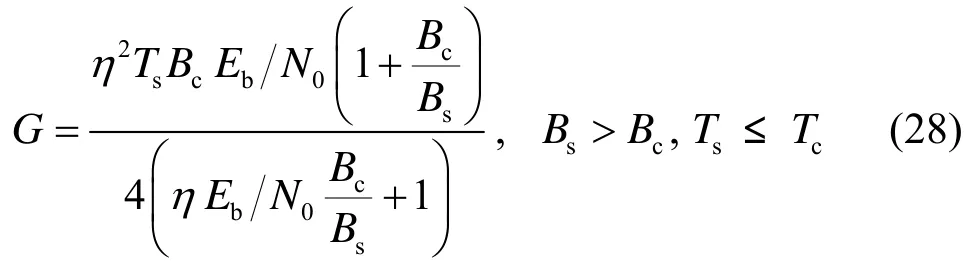
由式(28)可知，当信号带宽远大于相干带宽且符号长度小于相干时间时，EbN0越大，处理增益越大；此外，扩频信号处理增益与符号长度成正比。

信号带宽无限增大时，对式(28)求极限：

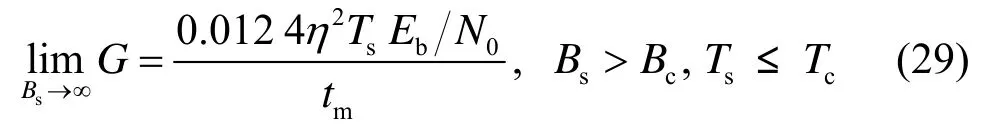
由式(29)可知当符号长度小于相干时间时，随着信号带宽的无限增大，处理增益不会无限增大。式(28)中，处理增益的表达式由2个多项式相除构成；同时，信号带宽无限增大时，处理增益存在极限。基于此，当时，处理增益是Ts、Bs的连续函数[13]。根据文献[13]中，连续函数在闭区间上必存在最大值，可以得出：信道衰落为频选慢衰落时，随着信号带宽的无限增大，扩频信号处理增益的上限存在，且由信道参数与信噪比确定。

考虑多径时延tm无穷小的情况，信道的相干带宽趋于无穷大，故频选慢衰落信道无限逼近于AWGN信道。此时，随着信号带宽的无限增大，式(30)所示的处理增益极限趋近于无穷大。这与AWGN信道中扩频信号处理增益的变化趋势一致。

③平坦快衰落

当Bs≤Bc，Ts＞Tc时，信道衰落为平坦快衰落。此时，根据式(14)、式(15)，式(26)可化简为

式(30)对df求偏导可知，当信号带宽小于相干带宽且符号长度远大于相干时间时，df越小，处理增益越大。从式(30)中还可以看出，在该种情况下，Eb/N0越大，处理增益越大；此外，扩频信号处理增益与信号带宽成正比。

符号长度无限增大时，对处理增益求极限：

由式(31)可知当信号带宽小于相干带宽时，随着符号长度的无限增大，处理增益不会无限增大。式(30)中，处理增益的表达式由2个多项式相除构成；同时，符号长度无限增大时，处理增益存在极限。基于此，当Ts∈[Tc,∞]、Bs∈[0,Bc]时，处理增益是Ts、Bs的连续函数[13]。根据文献[13]中，连续函数在闭区间上必存在最大值，可以得出：信道衰落为平坦快衰落时，随着符号长度的无限增大，扩频信号处理增益的上限存在，且由信道参数与信噪比确定。

考虑最大多普勒频移fd无穷小的情况，信道的相干时间趋于无穷大，故平坦快衰落信道无限逼近于AWGN信道。此时，随着符号长度的无限增大，式(32)所示的处理增益极限趋近于无穷大。这与AWGN信道中扩频信号处理增益的变化趋势一致。

④频选快衰落

当Bs＞Bc，Ts＞Tc时，信道衰落为频选快衰落。此时，根据式(14)、式(15)，式(26)可化简为

式(32)对fd求导可知，当信号带宽大于相干带宽且符号长度大于相干时间时，fd越小，处理增益越大；从式(32)中还可以看出，在该种情况下，Eb/N0越大，处理增益越大。

信号带宽或符号长度无限增大时，对处理增益求极限：

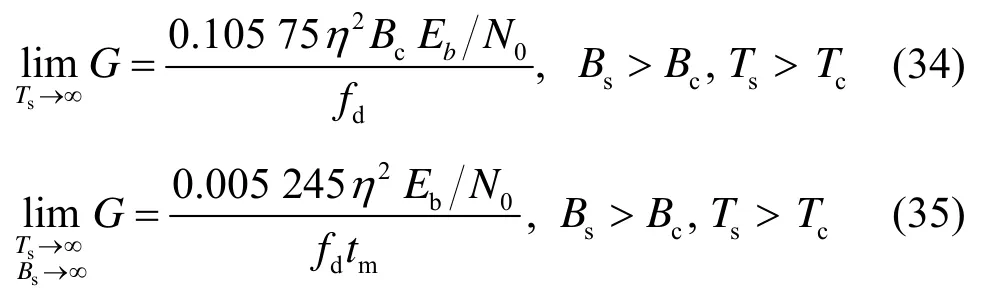
由式(33)～式(35)中的3组极限可知，随着信号带宽无限增大或者符号长度无限增大，处理增益不会无限增大。式(32)中，处理增益的表达式由2个多项式相除构成；同时，信号带宽或符号长度无限增大时，处理增益存在极限。基于此，当时，处理增益是sT、sB的连续函数[13]。根据文献[13]中，连续函数在闭区间上必存在最大值，可以得出：信道衰落为频选快衰落时，随着信号带宽或符号长度的无限增大，扩频信号处理增益的上限存在，且由信道参数与信噪比确定。

考虑最大多普勒频移fd无穷小且多径时延tm无穷小，信道的相干时间以及相干带宽均趋于无穷大，故频选快衰落信道无限逼近于AWGN信道。此时，随着信号带宽或符号长度的无限增大，式(36)所示的处理增益极限趋近于无穷大。这与AWGN信道中扩频信号处理增益的变化趋势一致。

综上所述，针对联合相干非相干检测算法，给定Eb/N0与多径信道参数时，扩频信号处理增益的上限存在。在上述条件下，若信号带宽或符号长度无限增大，扩频增益无限增大，接收机的输入信噪功率比无限下降，但由于扩频信号实际获得的处理增益不能超过其上限，接收机检测信号的输出信噪比无限低，使得接收信号无法被正确解调。然而，在最大多普勒频移fd无穷小、多径时延tm无穷小的情况下，多径衰落信道无限逼近于AWGN信道。此时随着信号带宽或符号长度的无限增大，处理增益无限增大。

基于上述分析，可以得出：多径衰落信道中，扩频信号处理增益的上限存在。该上限存在的原因是：多径衰落信道中，当信号的时频二维区域超过信道的相干区域时，相干检测不能直接使用[4]，取而代之的是联合相干非相干检测。其中，在相干区域内进行导引辅助的相干检测时，由于信道估计受噪声影响，信道估计值与信号共轭相乘产生了噪声的二次项。Eb/N0恒定时，随着信号带宽或者符号长度的无限增大，接收机的输入信噪功率比无限下降，又因为相干区域的大小受限，所以相干区域内的信道估计值受到的噪声影响逐渐增大。由式(24)～式(26)可知，在该种情况下，信道补偿过程中产生的噪声二次项逐渐增大，并且超越噪声一次项成为决定输出噪声功率的主要因素，此时联合相干非相干检测的输出信噪比急剧恶化，故处理增益不能无限增大。

4 数值与仿真结果

以联合相干非相干检测算法为基础，本部分利用 MATLAB仿真软件仿真了时频二维扩频信号的处理增益，同时根据式(28)、式(30)、式(32)计算出扩频信号处理增益的理论值，最后简要分析了扩频信号处理增益的性质。为了得到精确的仿真结果，处理增益的仿真值是通过对多个符号的仿真值进行平均得到的，用于平均的符号个数等于仿真时间除以符号长度，其中，仿真时间为200s。数值与仿真分析基于表1所示的参数设置。

表1 数值与仿真分析的参数设置

4.1 处理增益的数值与仿真结果

如图2～图5所示，处理增益的仿真曲线与理论曲线基本相符，但数值上存在着不超过3dB的差异。其原因在于：理论分析中，相干区域内信道响应是假设完全相关的，即信道响应的时域相关系数为1，频域相关系数也为 1；而仿真过程中，相干区域内信道响应是部分相关的，其时域相关系数不超过0.5[11]，频率相关系数不超过0.9[12]。因而，输出信噪比的仿真值比理论值低，进一步使得处理增益的仿真值比理论值低。

图2给出了 Eb/ N0取不同值时，处理增益随信号带宽变化的理论与仿真曲线；图3给出了最大多普勒频移取不同值时，处理增益随信号带宽变化的理论与仿真曲线。

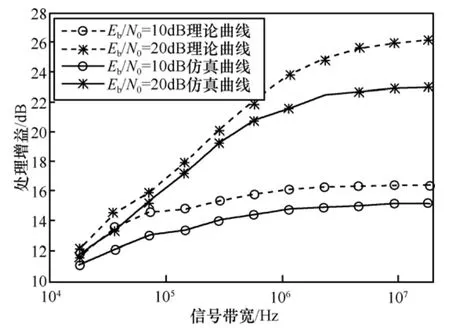
图2 处理增益随信号带宽变化的理论与仿真曲线（符号长度 Ts= 0 .002 25s ，多径信道的最大多普勒频移 fd= 1 00Hz ）

图3 处理增益随信号带宽变化的理论与仿真曲线（符号长度 Ts= 0 .09s ，信噪比 Eb N0= 2 0dB ）

从图2、图3可以看出：给定符号长度时，随着信号带宽的增大，处理增益并非线性增大，而是无限趋近式(29)、式(33)给出的极限值。其原因在于：在相干区域内进行导引辅助的相干检测时，由于信道估计受噪声影响，信道估计值与信号共轭相乘产生了噪声的二次项。 Eb/N0恒定时，随着信号带宽的无限增大，接收机的输入信噪功率比无限下降，又因为相干区域的大小受限，所以相干区域内的信道估计值受到的噪声影响逐渐增大，式(24)中的噪声二次项会迅速超越噪声一次项，并成为决定输出噪声功率的主要因素。根据式(25)，此时联合相干非相干检测的输出信噪比急剧恶化。

图2表明了给定符号长度时，随着信号带宽的无限增大，若 E b/ N0增大，则输入信噪功率比增大，进而相干区域的信道估计值受噪声影响减小，噪声二次项引起的信噪比损失减小，故处理增益增大。图3表明了当符号长度大于相干时间时，最大多普勒频移越小，能实现相干检测的相干区域越大，故处理增益越大。

图4 处理增益随符号长度变化的理论与仿真曲线（信号带宽Bs= 8 kHz ，多径信道的最大多普勒频移 fd= 1 00Hz ）

图5 处理增益随符号长度变化的理论与仿真曲线（信号带宽 Bs= 8 kHz 、信噪比 E b/N0= 2 0dB ）

图4给出了 Eb/N0取不同值时，处理增益随符号长度变化的理论与仿真曲线；图5给出了最大多普勒频移取不同值时，处理增益随符号长度变化的理论与仿真曲线。

从图4、图5可以看出：给定信号带宽时，随着符号长度的增大，处理增益并非线性增大，而是无限趋近式(31)、式(34)给出的极限值。其原因在于：在相干区域内进行导引辅助的相干检测时，由于信道估计受噪声影响，信道估计值与信号共轭相乘产生了噪声的二次项。 Eb/N0恒定时，随着符号长度的无限增大，接收机的输入信噪功率比无限下降，又因为相干区域的大小受限，所以相干区域内的信道估计值受到的噪声影响逐渐增大，式(24)中的噪声二次项会迅速超越噪声一次项，并成为决定输出噪声功率的主要因素。根据式(25)，此时联合相干非相干检测的输出信噪比急剧恶化。

图4表明了给定信号带宽时，随着符号长度的无限增大，若 Eb/N0增大，则输入信噪功率比增大，进而相干区域的信道估计值受噪声影响减小，噪声二次项引起的信噪比损失减小，故处理增益增大。图5表明了当符号长度大于相干时间时，最大多普勒频移越小，能实现相干检测的相干区域越大，故处理增益越大。

4.2 处理增益上限存在的原因

3.2节分析了处理增益不能无限增大的原因。从分析中可以看出，随着信号带宽或者符号长度的无限增大，噪声二次项的迅速增大是导致扩频信号处理增益存在上限的原因。本节将针对噪声二次项对输出信噪比的影响，给出其数值与仿真结果。

假设接收信号中的加性白高斯噪声是接收机内部的热噪声，当环境温度为290K时，白噪声的功率谱密度为 N0=-1 74dBm/Hz 。

图 6给出了不同信号带宽下，联合相干非相干检测算法的输出信号功率、输出噪声一次项的功率以及输出噪声二次项的功率。如图6所示，信号带宽增大时，输出信号功率与输出噪声的一次项功率变化一致，都为先降低后保持不变；而输出噪声的二次项功率则先降低后线性增加。式(24)中输出噪声总功率为噪声的一次项功率与二次项功率之和。因此，随着信号带宽的无限增大，输出信号功率保持不变，但输出噪声二次项的功率却无限增大，则输出信噪比会无限下降，故处理增益不能无限增大。

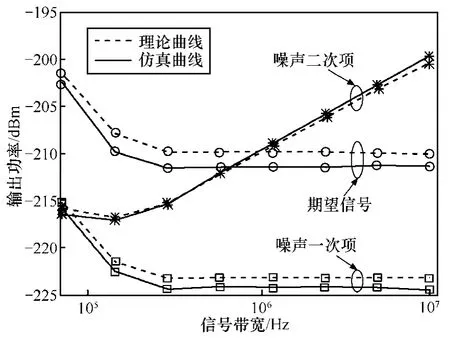
图6 不同信号带宽下，输出信号功率、输出噪声一次项、噪声二次项的功率（符号长度 Ts= 0 .09s ， Eb /N0= 2 0dB，多径信道的最大多普勒频移 fd= 1 00Hz）

图7给出了不同符号长度下，联合相干非相干检测算法的输出信号功率、输出噪声一次项的功率以及输出噪声二次项的功率。如图7所示，符号长度增大时，输出信号功率与输出噪声的一次项功率均保持不变，而输出噪声的二次项功率则线性增加。式(24)中输出噪声总功率为噪声的一次项功率与二次项功率之和。因此，随着符号长度的无限增大，输出信号功率保持不变，但输出噪声二次项的功率却无限增大，则输出信噪比会急剧下降，故处理增益不能无限增大。

图7 不同符号长度下，输出信号功率、输出噪声一次项、噪声二次项的功率（信号带宽 Bs= 8 kHz ，信噪比 Eb/N0= 2 0dB，多径信道最大多普勒频移 fd= 1 00Hz）

从图6～图7中可以看出，在多径衰落信道中，EbN0恒定时，随着信号带宽或符号长度的无限增大，输出噪声一次项的功率保持不变，但输出噪声二次项的功率却无限增大。当信号带宽或符号长度增大到一定程度时，噪声二次项便超越噪声一次项，并成为了决定输出噪声功率的主要因素，此时输出信噪比会急剧下降，扩频信号的处理增益不能无限增大，即扩频信号处理增益的上限存在。

综上所述，针对联合相干非相干检测算法，在充分散射的多径衰落信道中，信号带宽或符号长度无限增大时，扩频信号的处理增益不会无限增大。从图 2～图 5给出的数值与仿真结果中容易看出：BPSK调制、20dB信噪比、100Hz最大多普勒频移、5×10-6负指数衰落因子的充分散射多径信道，扩频信号的处理增益不超过30dB。

5 结束语

本文考虑充分散射多径衰落信道中的BPSK调制扩频信号，针对联合相干非相干检测算法，分析得到信号带宽无限增大或符号长度无限增大时，扩频信号的处理增益不能无限增大；处理增益的上限由信道参数与信噪比确定。究其原因，当信号带宽或符号长度无限增大时，接收机的输入信噪功率比无限下降，并且由于相干区域的大小受限，其相干区域内的信道估计值受到的噪声影响逐渐增大。此时，信道补偿过程中产生的噪声二次项逐渐增大，并且超越噪声一次项成为决定输出噪声功率的主要因素，故联合相干非相干检测的输出信噪比急剧恶化。但是当最大多普勒频移无穷小、多径时延无穷小时，多径衰落信道无限逼近于 AWGN信道，在该种情况下，随着信号带宽或符号长度的无限增大，处理增益无限增大。综上所述，本文对多径衰落信道中扩频信号处理增益上限的研究，可以从理论上指导需要隐蔽无线通信的工程应用。

[1] 曾一凡, 李晖. 扩频通信原理[M]. 北京: 机械工业出版社, 2005.ZENG Y F, LI H. Principles of Spread Spectrum Communication[M].Beijing: China Machine Press, 2005.

[2] FAZEL K, KAISER S. Multi-carrier and Spread Spectrum Systems:from OFDM and MC-CDMA to LTE and WiMAX[M]. Germany:John Wiley and Sons Ltd , 2009.

[3] SCHILLING D, MILSTEIN L, PICKHOLTZ R. et al. Optimization of the processing gain of an Mary direct sequence spread spectrum communication system[J]. IEEE Transactions on Communications, 1980,28(8): 1389-1398.

[4] BLUMENSTEIN J, FEDRA Z. The characteristics of the 2D spreading based communication systems[A]. RADIOELEKTRONIKA '09 19th International Conference[C]. Bratislava, Slovakia, 2009. 279-281.

[5] VARZAKAS P. Optimizing processing gain of a cellular DS/FFHCDMA Rayleigh fading system[A]. ISSSTA '08 IEEE 10th International Symposium on Spread Spectrum Techniques and Applications[C]. Bologna, Italy, 2008. 523-527.

[6] 邵士海, 唐友喜, 戚骥等. 多径衰落信道中导引符号辅助的二维扩频相干解调的性能分析[J]. 电子学报, 2005, 33(4): 689-691.SHAO S H, TANG Y X, QI J, et al. Performance analysis of pilot symbol assisted two dimensional spread spectrum systems in multi-path fading channels[J]. Chinese of Journal Electronics, 2005, 33(4): 689-691.

[7] BANANI S A, VAUGHAN R G. OFDM with iterative blind channel estimation[J]. IEEE Transactions on Vehicular Technology, 2010,59(9): 4298-4308.

[8] BAINS R, MULLER R, KALIS A. Link performance of an ESPAR-antenna array in rich scattering and clustered channels[A].ISWCS 2007 4th International Symposium on Wireless Communication Systems[C]. Trondheim, Norway, 2007. 308-312.

[9] PROAKIS J G. Digital Communications[M]. NewYork: McGraw-Hill,2009.

[10] MOLISCH A F. Wideband Wireless Digital Communications[M]. NJ:Pearson Education, 2008.

[11] RAPPAPORT T S. Wireless Communication Principles and Practice[M]. NJ: Pearson Education, 2009.

[12] ZHANG Q T, SONG S H. Exact expression for the coherence bandwidth of Rayleigh fading channels[J]. IEEE Transactions on Communications, 2007, 55(7): 1296-1299.

[13] 朱来义. 微积分[M]. 北京: 高等教育出版社, 2009.ZHU L Y. Calculus[M]. Beijing: Higher Education Press, 2009.