双光子通道中任意初态原子比特周期量子回声的调控

周并举，刘小娟，詹杰，周仁龙

（湖南科技大学 物理学院，湖南 湘潭 411201）

1 引言

量子态是量子信息的载体。量子信息处理（量子通信和量子计算）是指以量子力学基本原理为基础，通过对量子态的各种相干特性进行计算、编码和传输的全新信息处理方式，在提高运算速度、确保信息安全、增大信息容量和提高检测精度等方面可以突破现有的经典信息系统的极限，成为研究热点[1]。

二能级原子是双量子态系统，称为原子比特，是实现量子通信和量子计算的信息载体。如原子比特在量子通用逻辑门中得到实现[2]，如在不破坏其量子相干性的情况下，可能将飞行光比特所载信息传送到静止原子比特上，并在需要时成功读取原子比特内存储的信息，这一技术将是未来量子信息处理中的重要组成部分[3]。

然而，原子比特、逻辑门等量子器件不可避免地会与环境相互作用，受到环境噪声的影响。目前，研究表明，环境噪声导致编码的量子态从量子相干叠加态退化为经典态，使原子比特消相干，给量子信息处理带来错误，严重阻碍了量子储存器的规模化，是阻碍量子计算的主要因素[4]。因此，在存在环境噪声条件下，量子通信的信息传输和量子计算的正常运转必然要考虑量子态的保真度问题[5]。保真度是量度量子态在外界干扰下回复的准确性，而在外界扰动下，保真度经过周期T之后，完全回复到初值，称之为量子态具有周期为T的量子回声[6]，有着广泛的应用。如在核磁共振实验中，量子自旋回声振幅的变化，是描述多体量子系统特性的有用工具[7]。获得原子比特量子回声成为量子信息领域中的重要任务。由于通常情况下，原子比特处于一种统计混合态，研究混合态原子比特的动力学行为不仅具有更普遍意义[8,9]，而且对存在量子噪声条件下的量子通信亦是十分重要的。由于双光子微波激射器成功运转[10]和双光子过程原子具有周期性量子力学通道的特性[11]，使双光子通道成为量子通信中正确传递量子信息的重要工具, 成为人们深入研究的热点。

本文选取相干光场作为原子比特的噪声环境，研究双光子通道中具有任意初态（纯态和混合态）原子比特保真度的时间演化，探索原子比特量子回声的产生条件。分别考察原子比特初态和环境参数对量子回声形成的影响，获得调控原子比特量子回声的参数，并揭示其物理实质。我们的研究结果对于存在环境噪声条件下，运用双光子通道中原子比特实验实现量子信息和量子计算是十分重要的。

2 理论模型及密度算符

考虑一个原子比特与单模辐射场相互作用双光子过程的量子系统。在旋波近似下，系统的哈密顿量表示为[9]

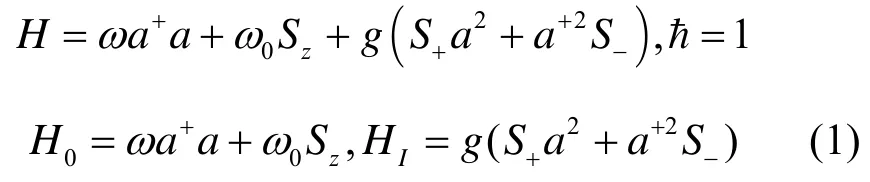
其中，a+、a是频率为ω的场模的产生和湮灭算符，SZ和S±分别为原子的反转和跃迁算符，ω0为原子的跃迁频率，g为原子和辐射场的耦合系数，考虑共振情况即 ω =ω0。

由相互作用哈密顿量HI决定的系统时间演化Dyson算符即为双光子通道：

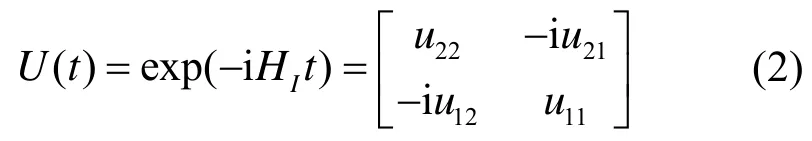
其中

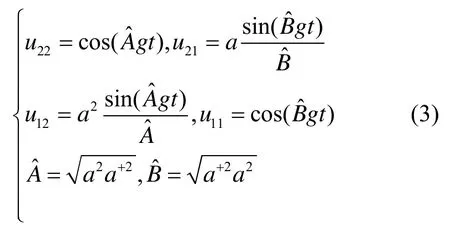
设光场初始处于相干态：

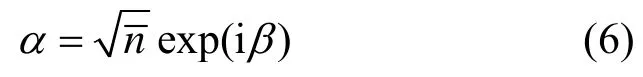
如果原子比特初始为激发态和基态任意叠加纯态，则任意时刻，双光子通道中原子比特约化密度算符可以写为式(8)。

其中，ϑ是原子比特分布角，φ是它的偶极位相，文计算中取0πϑ≤≤，02πφ≤≤。

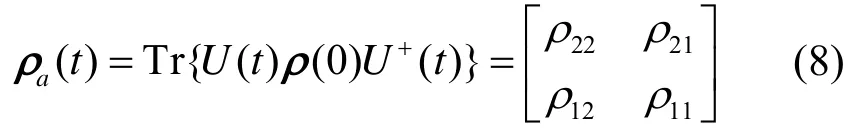
其中，全系统（光场+原子比特）初始密度矩阵：

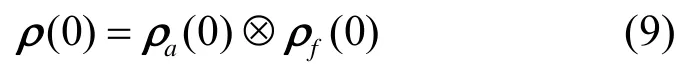
而 ρf(0)和ρa(0)分别为光场和原子比特初始密度矩阵。则 ρa(t )的矩阵元为

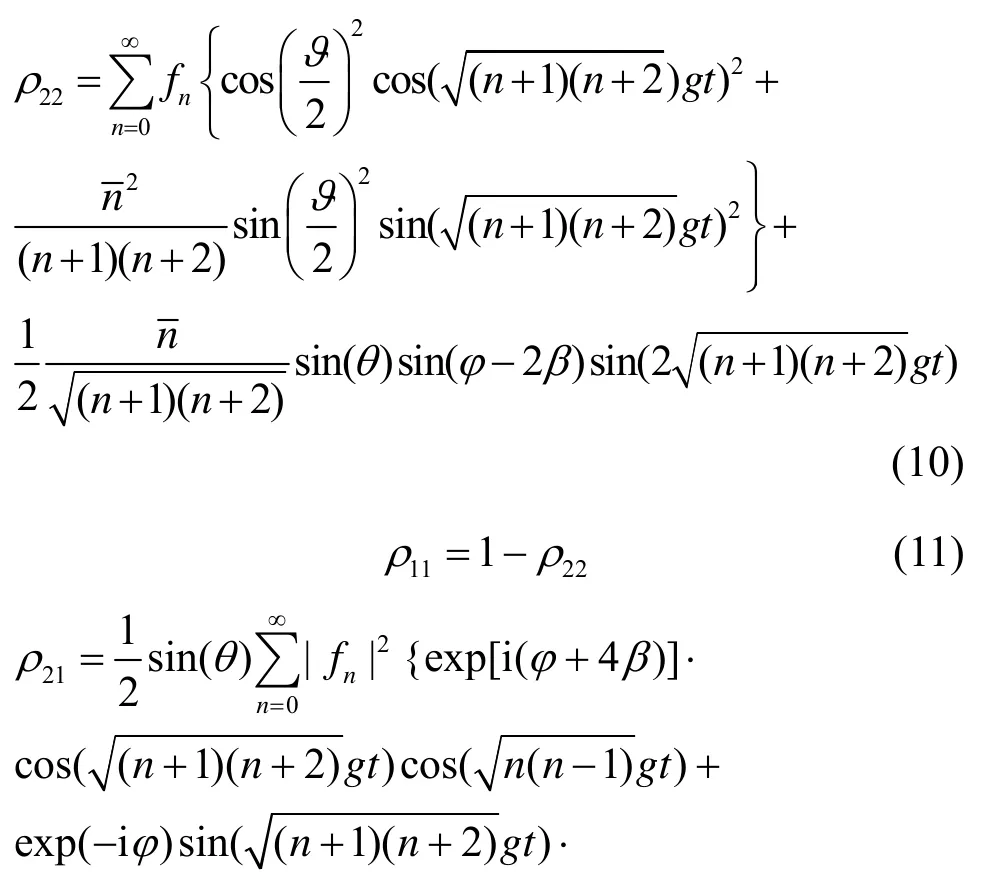
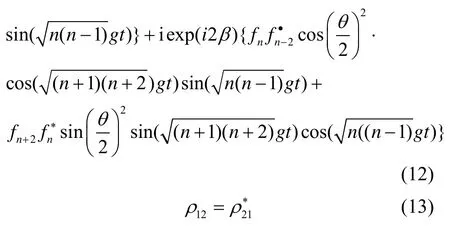
若考虑原子比特初始处于任意混合态

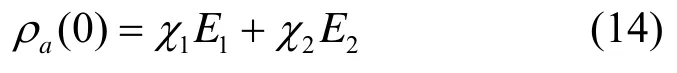
其中，E1=|-＞＜-|表示基态，E2=|+＞＜+|为激发态。χi为原子比特处于态Ei（i=1,2）的概率，且χ1+χ2=1，则在任意时刻t＞0，原子的约化密度算符可以写为

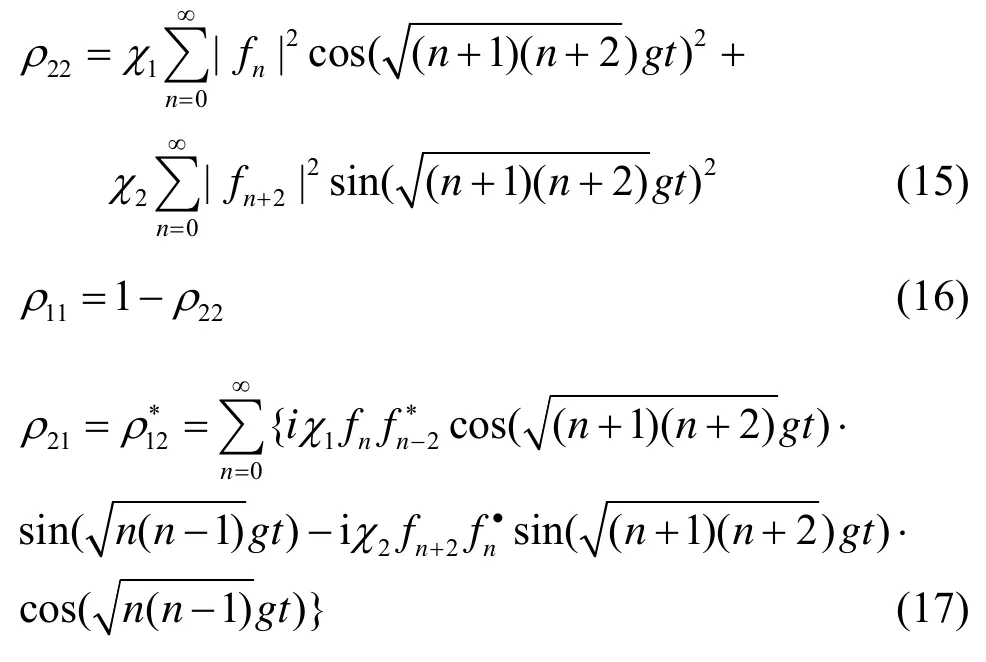
利用式(11)～式(17)，可以根据原子比特和光场的初态分布情况，研究原子比特（量子）态保真度，探讨原子比特量子回声产生的条件。

3 保真度及周期量子回声

3.1 保真度的定义

为了描述输入量子态ρ(0)(初态)和输出量子态ρ(t )(终态)的偏差程度，人们引入量子态保真度，其定义为[5]

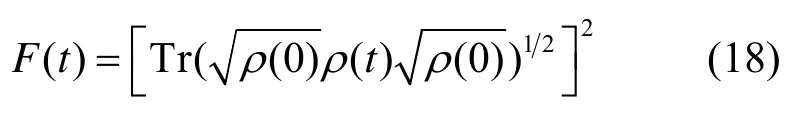
F( t)取值范围在0～1之间，当F( t)=0时，量子态的初态和末态相互正交，表示信息在传输过程中完全失真；当F( t)=1时，初态和末态完全相同，表示信息理想传输过程。一般情况下，0＜F( t)＜1，表示初态和末态部分重叠，信息在传输过程中存在失真现象。

这样，由式（7）表达的原子初始纯态，原子比特态保真度表达式为

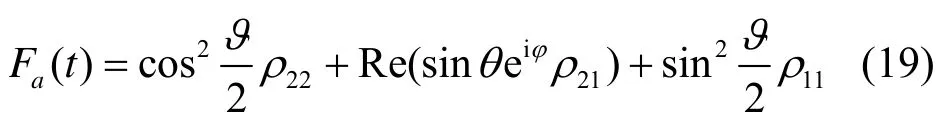
而式(14)表达的原子比特初始处于任意混合态时，原子比特态保真度表达式为

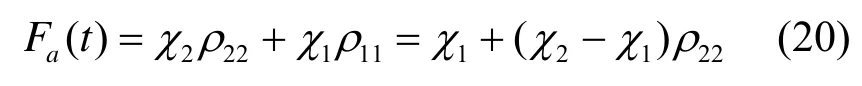
3.2 周期量子回声

当原子比特态保真度满足以下等式

Fa( t)=Fa( t+nT),n =0,1,2,…时，

且

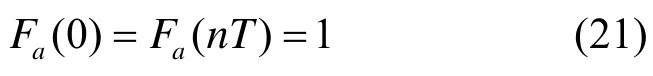
关系成立时，称为原子比特产生了周期为T的量子回声。

4 数值讨论

在第3节的基础上，本节分别讨论不同原子比特初态和光场（环境）参数对原子比特态保真度的影响，研究量子回声产生和控制。

首先，考察原子比特初态参数变化的影响。取环境参数确定，即取光场平均光子数=36，位相角β=0。

4.1 原子比特初始处于任意纯态

图1表明了原子比特初始的分布角θ从0→π/4→π/2变化时，原子比特态保真度Fa( t)的时间演化。显然，Fa( t)呈周期性变化。

由图1(a)看出，原子比特初始处于非相干纯态（激发态）时，在t=nπ(n=0,1,2,…)时刻附近，Fa( t)几乎在0～1之间振荡，在其余时间保持值0.5。随着原子分布角θ增大，θ→π/4，在t=nπ(n=0,1,2,…)时刻，Fa( t)的最小值增大，而在其余区间，随时间呈余弦函数形演化，如图1(b)所示。

这些规律源于式(19)。首先，当θ=0,Fa( t)只有第一项：即

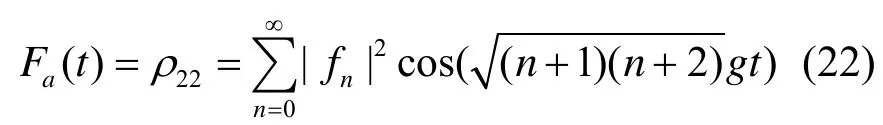
其中，

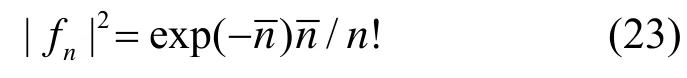
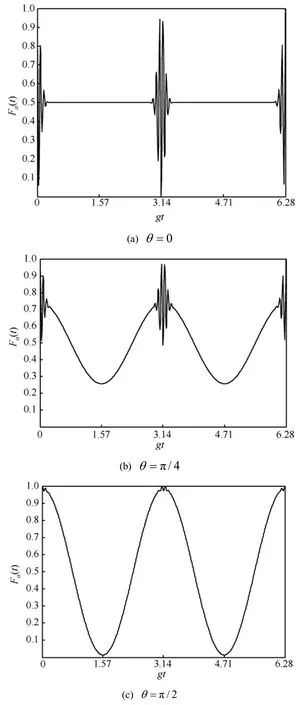
图1 原子比特态保真度时间演化(=36,β=0)

特别地，当π/2θ=时，由式(7)可知原子比特初始处于等概率叠加态，即

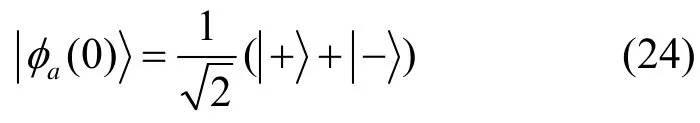
保真度随时间作余弦周期演化，如图1(c)所示。在t=nπ(n=0,1,2…)时刻，Fa( t)达到最大值1，而在t=nπ/2(n =0,1,2…)时刻，Fa( t)为0。显然满足

Fa( t)=Fa( t+nπ )，t=π,n=0,1,2…

并且有

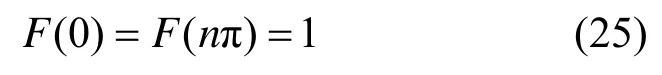
成立。这表明原子比特产生了具有周期为π的量子回声。其物理实质分析如下。

因与式(15)～式(17)决定的原子比特约化密度算符对应的本征矢分别为[12]

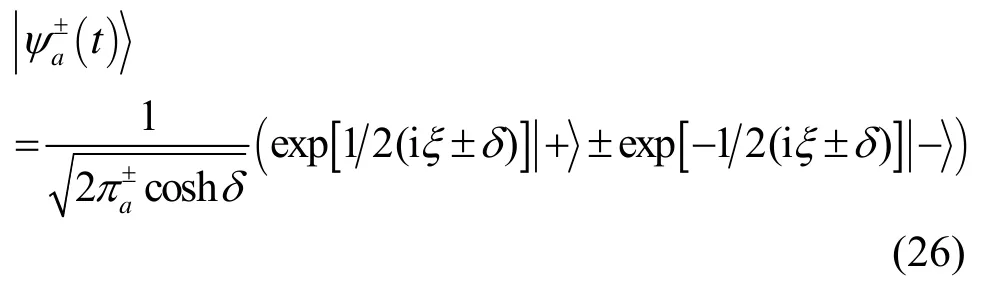
其中

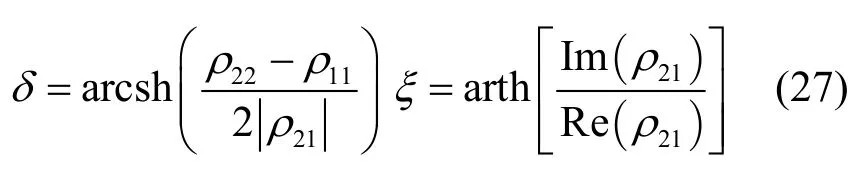
对应的本征值表示为[11]

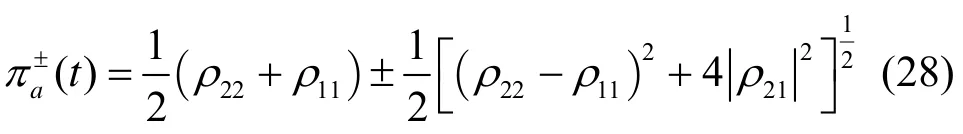
根据Schmidt分解定理[12]，可把全系统任意时刻的态矢表示为

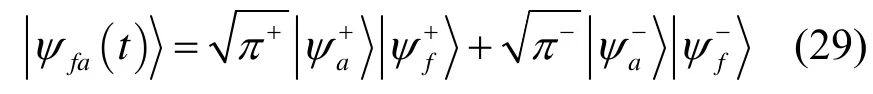
将参数θ=π/2,t=nπ(n=0,1,2…)代入式(25)和式(26)，得π+=1,π-=0,δ=0,ξ=0。显然，式(29)化为，这正是原子比特与光场完全退纠缠的直积态。而原子比特演化到态，这正是原子比特初态式(24)。因此，原子比特产生周期为π的量子回声，物理实质是原子比特与环境完全退纠缠。

而在t=nπ/2(n=0,1,2,…)时刻，π+=π-=1/2，原子与场处于最大纠缠态（EPR态），原子比特处于完全失真的混合态，保真度为0，与数值计算结果完全一致。

4.2 原子初始为混合态

图2展示了原子比特初始处于混合态的情况。

定义η=|χ1-χ2|，即原子比特态概率差，与原子比特混合度成反比。当η=1(χ1, χ2=0or1)，原子比特初始处于纯态（基态或激发态），混合度为0；η=0(χ1=χ2=1/2)，原子比 特初始处于最大混合态；0＜η＜1，原子比特处于一般混合态。

图2(a)表明了η=1时Fa( t)的演化，与图1(a)完全一致。图2(b)表明了η=0.4时Fa( t)的演化，与图2(a)相比较，演化周期相同，但振幅变小；图2(c)表明了η=0原子比特初始处于最大混合态保真度演化，此时，保真度为定值Fa( t)=0.5。

这些结果源于：当η=1(χ1=0,χ2=1)，代入式(20)，保真度表达式为

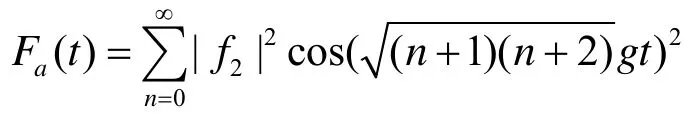
与式(19)完全相同，故图1(a)与图2(a)演化曲线一致。当01,η＜＜保真度由直流成分1χ和交流成分(χ1-χ2)ρ222部分组成，Fa(t)的周期不变，但幅度受原子的混合度调制，随混合度的增加幅度减小，因此0＜Fa(t)＜1。当η=0(χ2=χ1=0.5), Fa(t)的交流成分消失，只有直流成分χ1起作用，因此，Fa( t)取稳定值0.5，如图2(c)所示。

下面，考察环境Fa(t)的影响，即调节光场参数，实现对原子比特周期量子回声的控制。选取原子初始为最大的相干态(θ=π/2)。

4.3 光场平均光子数的调节

4.4 光场位相的调节

图4表明，光场位相角β从0→π/4→π/2,原子比特周期量子回声产生平移。β增加π/2时，与β=0时一致。表明光场位相可以调控原子比特量子回声的位相，使之产生平移。

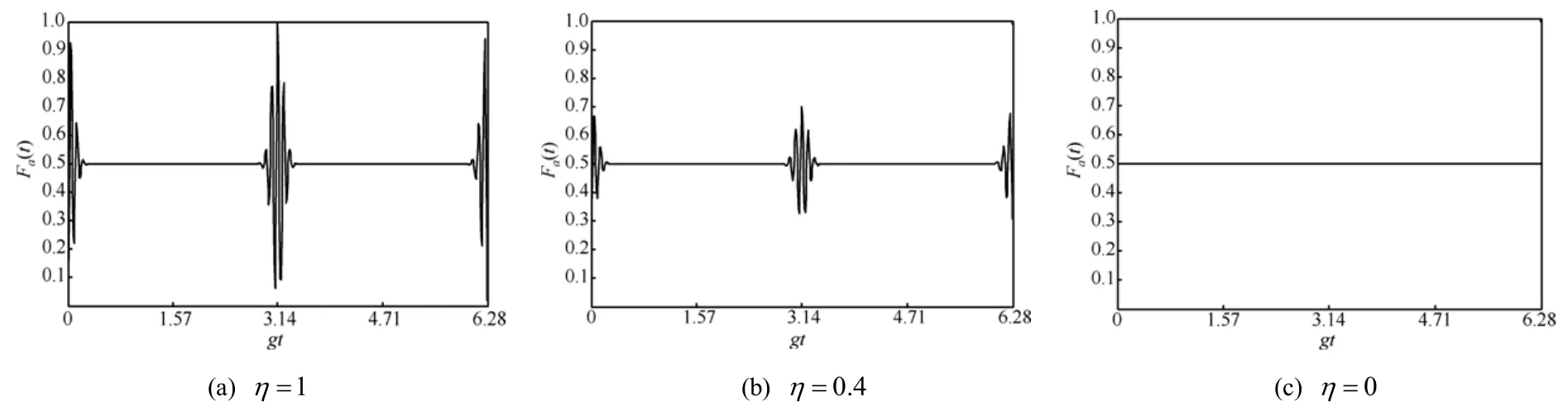
图2 原子比特态保真度时间演化(=36,β=0)

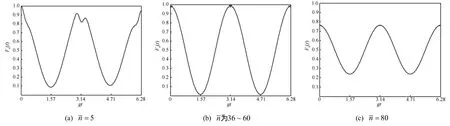
图3 原子比特态保真度时间演化(θ=π/2,β=0)

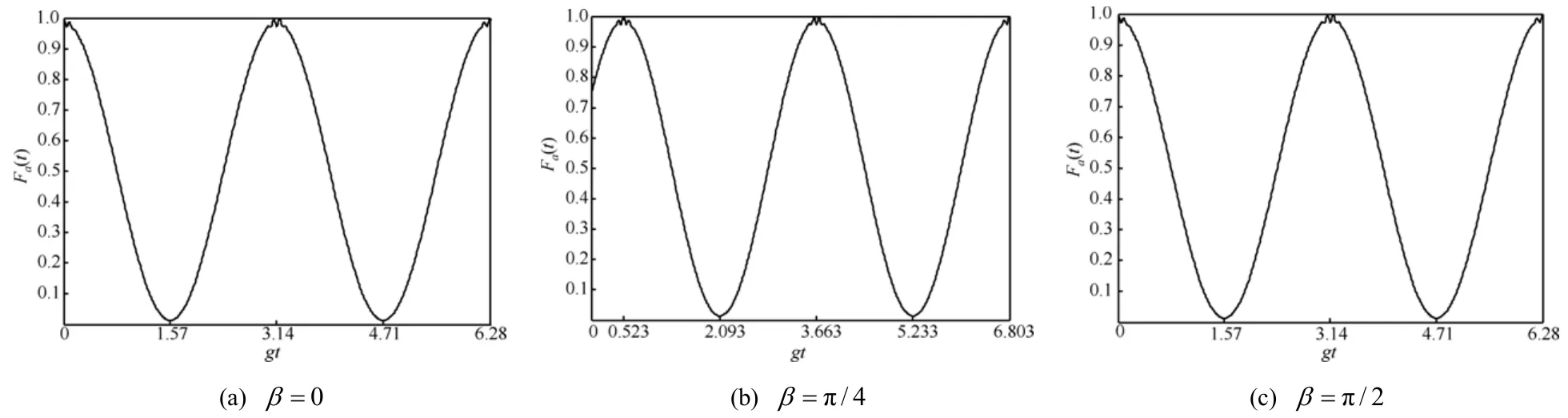
图4 原子比特态保真度时间演化(θ= π /2,= 3 6)

5 结束语

本文运用全量子理论，研究了相干光场为环境下的双光子通道中任意初态原子比特的量子态保真度的演化, 探讨了原子比特周期量子回声的产生与调控。结果表明如下：1) 在光场参数一定的情况下，原子比特态保真度呈周期性演化，选择原子比特初始处于最大相干纯态(π/2θ=)，产生周期量子回声，其物理实质是原子比特与光场完全退纠缠；2) 原子比特初始处于任意混合态时，原子比特态保真度振幅受混合度调制，不出现周期量子回声；3) 光场平均光子对原子比特量子回声振幅产生非线性影响，控制平均光子数在 36～60左右，可以获得稳定的原子比特周期量子回声；4) 调节光场位相角β，可控制原子比特量子周期回声的位相，使之产生平移。

以上结果对于应用双光子通道中原子比特量子回声的实现量子信息处理有着重要意义。

[1] BENNETT C H, DIVINCENZO D P. Quantum information and computation[J]. Nature (London) , 2000, 404: 247-255.

[2] MEIER F, LEVY J, LOSSL D. Quantum computing with spin cluster qubits[J]. Phys Rev Lett, 2003, 90(4): 047901-047904.

[3] 吴长锋. 我国首次实现光子比特与原子比特间的量子隐形传态[J].前沿科学, 2008, 2(5):92.WU C F. Quantum teleportation between the photon bits and atoms bits first is completed in China[J]. Frontier Science, 2008, 2(5):92.

[4] LONG G L, LI Y S, ZHANG W L, et al. Dominant gate imperfection in grovers′ quantum search aglorith[J]. Phys Rev A, 2000, 61(4):0423051-0423055.

[5] LIU T K, WANG J S, LIU X J, et al. Fidelity of quantum information in a pair atoms of entanglement state interacting with cohere state[J]Acta Optica Sinica, 2000,20:1449-1455.

[6] SANKARANARAYANAN R, JANC H, LAKSHMANAN M. Quantum Dynamical Echo in Two-Level Systems[P]. SI/050618vl-6,2005.

[7] SANKARANARAYANAN R, JANC H, LAKSHMANAN M. Dynamical echo in two-state quantum systems[J]. Chaos, Solitons and Fractals, 2007, 33: 1618-1624.

[8] 聂义友, 郑富年, 刘三秋等. 混合态二能级原子双光子过程中原子的压缩效应[J]. 电子学报, 2002, 19(1):38.NIE Y Y, ZHENG F N, LIU S Q, et al. Atomic squeezing effects in a two-photon with two-level atomic mixed-state[J]. Chinese Journal of Quantum Electronics, 2002, 19(1):38.

[9] 刘小娟, 周并举, 方卯发等. 双光子过程中任意初态原子信息熵压缩[J]. 物理学报,2006, 55(2):704-711.LIU X J, ZHOU B J, FANG M F, et al. Information entropy squeezing of the atom of an arbitrary initial state via the two-phtoton process[J].Acta Phys Sin, 2006, 55(2): 704-711.

[10] 方卯发, 刘翔. 双光子 Jaynes-Cummings 模型中量子力学通道与量子互熵[J]. 物理学报, 2000, 49(3): 0435-0440.FANG M F, LIU X. Quantum mechanical channel and quantum mutual entropy in the two-photon Jaynes-Cummings[J]. Acta Phys, Sin,2000, 49(3): 0435-0440.

[11] 刘小娟, 方卯发, 周清平. 具有原子运动的双光子 J-C模型中量子力学通道与量子互熵[J]. 物理学报, 2005, 54(2): 703-709.LIU X J, FANG M F, ZHOU Q P. Quantum mechanical channel and quantum mutual entropy in the two-photon Jaynes-Cummings with atomic motion[J]. Acta Phys Sin, 2005, 54(2): 703-709.

[12] ZHOU B J, LIU Y M, ZHAO M Z, et al. Preparation and control of atomic optimal entropy squeezing states for a moving two-level atom under control of the two-mode squeezing vacuum fields[J]. Chin Phys B, 2010, 19(12): 1242071-1242076.