基于谓词抽象的测试用例约简生成方法
2012-08-10郭曦张焕国
郭曦,张焕国,2
(1. 武汉大学 计算机学院,湖北 武汉 430072;2. 武汉大学 空天信息安全与可信计算教育部重点实验室,湖北 武汉 430072)
1 引言
软件开发是一个不断迭代和演化的过程,需要频繁地进行测试,同时测试用例集的规模随着测试需求的变更在不断地增大,此时不可避免地存在冗余的测试用例,即测试用例集的某个子集也满足所有的测试需求。由于测试用例在设计和维护等阶段均有较大开销,因而在满足测试需求的基础上,有必要生成约简的测试用例集,其目标是设计并使用一组数量较少的测试用例满足给定的测试需求,在提高软件测试效率的同时降低测试成本。
目前,测试用例约简[1]的方法是:首先针对每个测试需求生成对应的测试用例,所有测试需求对应的测试用例组成初始的测试用例集;再使用启发式方法、整数规划方法等对这个初始的测试用例集进行约简,去掉冗余的测试用例。这种方法的缺点在于它的效果取决于最初选定的测试用例集,不能完全实现根据测试目标对测试用例集的整体优化。此外,与测试用例集约简相关的测试用例集的错误检测效率问题也引起研究人员的关注,先后提出了多种测试用例优先级技术,以提高测试用例集的错误检测效率。
软件系统状态空间的大小和对应的测试用例集的数量有直接关系,最坏情况下,软件系统的状态空间和系统的规模呈指数关系。在测试过程中,往往因为模型的状态空间爆炸问题而难以产生精简的测试用例集,从而影响对软件系统所具有的性质的验证效率。谓词抽象是一类特殊的属性保持的抽象方法,是解决或者缓解状态空间爆炸最有效的方法之一[2],谓词在原始模型的状态空间上定义了一个等价关系,通过状态集合之间的映射,把原始模型转换成为一个易于处理的、包含有限状态的抽象模型。在抽象模型中成立的性质,在原始模型中也成立,而在抽象模型中不能证明真伪的性质,在原始模型中可能成立,也可能不成立。在测试用例生成阶段,通常利用谓词抽象自动验证工具的反例抽象精化功能:为了生成满足某个性质p的测试用例,在程序中检验p¬的满足情况,若出现反例,则表明可以生成满足p的测试用例;若找不出反例,则表明没有测试用例与p对应。
针对大规模软件系统状态迁移数量庞大,容易导致状态空间爆炸,从而难以生成精简的测试用例集对软件系统所具有的性质进行验证的问题,本文以系统状态的迁移作为研究对象,提出一种基于谓词抽象的测试用例约简生成方法。首先通过谓词在原始系统的状态空间上定义等价关系,得到状态约简的抽象模型;然后基于抽象模型的状态迁移关系,给出针对每个等价类的测试用例约简生成算法,从而在降低原始模型状态冗余的情况下生成约简的测试用例集。
2 相关工作及存在的问题
对于软件系统M,设其测试目标是由m个测试需求组成的集合R={r1, r2,…,rm},同时对每个测试需求生成n个测试用例集T={t1, t2,…,tn}。现有的测试用例集约简方法通过寻找T的某个子集,用尽可能少的测试用例满足测试需求集R。可以证明,测试用例集的约简是一个NP-C问题[3],故一般采用启发式算法来获得近似解。
Chvatal等人提出贪心(greedy)算法(G算法)来求解测试用例集约简问题[4],它每次从测试用例集T中选择一条测试用例,使它能最大程度上满足测试需求集R中未被满足的需求,然后从R中删除这些已被满足的需求,直到所有的需求都被满足,最坏情况下,该算法的时间复杂度为O( mn·min(m, n))。
Harrold提出了一种启发式方法[1],它根据测试用例的重要性来选择测试用例(HGS算法)。对于测试需求Ri和Rj,如果i<j,则该算法认为在重要程度上,Ri对应的测试用例比Rj对应的测试用例要高。该方法首先将测试需求r1, r2,…,rm划分到集合R1, R2,…,Rk( k≤n)中,其中Ri( i=1,2,…,k )为所有被T中i个测试用例所满足的测试需求,即首先选出集合R1对应的测试用例,然后使用贪心算法选择满足R2的测试用例,直到R2对应的测试需求均被满足,再依次处理集合中剩下的测试需求,最坏情况下,该算法的时间复杂度为O( m( m+n) k)。
Chen等人在贪心算法的基础上提出GE算法和GRE算法[5]。GE算法使用必不可少策略挑选出初始的测试用例集,再通过贪心算法对其进行约简,其时间复杂度仍为O( mn·min(m, n))。GRE算法循环交替使用1-1冗余策略以及必不可少策略生成初始测试用例集,再通过贪心算法选择其他的测试用例以满足剩下的测试需求。最坏情况下,GRE算法的时间复杂度为O(min(m, n)( m+n2k)),k表示一个测试用例最多能满足的测试需求的个数。
Lee等人提出的整数规划方法[6]将最小代表集的选择问题转换为整数规划问题,在理论上可以生成满足R的最优测试用例集,但该算法的运算开销呈指数级增长,计算复杂性也较高。
以上这几种算法都是针对测试用例集的简化策略,章晓芳等[7]在上述方法的基础上提出一种对测试需求进行约简的测试用例集优化方法,通过建立测试用例集和测试需求集之间的映射,判断是否存在一个测试用例满足多个测试需求的情况。程亮等[8]结合安全操作系统的对测试的需求,提出了简并测试集,设计基于安全状态转移的测试集生成方法。
目前,现有的测试用例集约简方法中,基于系统的状态空间约简的研究较少。徐明迪等[9]采用标记变迁系统对可信计算平台信任链进行测试,从易测性对信任链的状态进行描述并对系统的动作进行约简,为测试用例构造方法提供了理论依据。本文在其基础上,进一步以软件系统的状态迁移作为研究对象,通过谓词抽象的方法对软件系统的初始状态集合进行等价类划分,这样可以有效地减少系统状态集合内部的冗余和后续约简计算的工作量,并依据等价的抽象状态集合以及抽象状态迁移关系生成约简的测试用例集,提高对软件系统所具有的性质进行验证的效率。
3 系统模型状态约简与等价类的问题求解
对于一个软件系统,理想的测试用例集是在满足测试需求的基础上,用例的数量要尽可能少。现有的二叉判定图和树型结构等约简测试用例的方法,都是以系统所能达到的状态作为操作对象。实际上,决定测试用例集规模的直接因素往往不是系统的状态数量,而是状态迁移的数量。
为了更好地表示软件系统的状态以及状态间的迁移关系,通过谓词抽象技术,使用谓词表示软件系统的状态变迁,可以有效地对大规模软件系统的状态进行约简。谓词抽象使用一组有限数量的谓词把系统表示为有限状态机模型,该模型就是对原始系统的一种抽象,它较原始系统有更小的状态集合,其中每一种状态属于一个等价类,每个等价类里面包含若干个满足谓词划分的原始状态。本节还证明了一个基于原始模型系统状态空间的问题:经过等价类划分后得到若干个子问题,其中每个等价类对应一个子问题,首先对子问题进行求解,再将各子问题的解组合起来就得到原问题的解,该方法可以用来指导构建基于原始模型的约简测试用例集。
3.1 抽象状态的形式化定义
设原始系统模型M的状态集合为C,初始状态集合为IC,状态迁移关系集合为RC,谓词在状态集合C上定义一个等价关系,该等价关系把原始模型的初始状态集合划分成若干个等价类,每个等价类包含一个或多个状态,2个状态等价当且仅当它们属于同一个等价类。对于一组谓词Φ=(φ1,φ2,…,φn),和一组与之对应的布尔变量B=(B1, B2,…,Bn),使用谓词公式φ来表示原始模型的状态C,并使用变量B1, B2,…,Bn上的一组正交布尔表达式来表示对应的抽象模型的状态集合A。抽象状态表示为A( B1, B2,…,Bn),其初始状态集合记为IA,每个抽象状态与一个等价类相对应。为了表示模型的原始状态和抽象状态之间的关系,给出如下定义。
定义1 抽象算子α把模型的原始状态φ映射到抽象模型对应的抽象状态:

定义2 精化算子γ将抽象模型对应的抽象状态映射到模型的原始状态:

对于抽象模型的抽象状态A( B1, B2,…,Bn),使用谓词φi替换其中对应的Bi,即可得到该抽象状态对应的所有原始状态。由定义1和定义2可知:原始状态与抽象状态是一对一的关系,而抽象状态与原始状态是一对多的关系。
3.2 基于等价类划分的问题求解
由于谓词在原始模型M的状态集合上定义等价关系,M中每一个状态属于一个等价类,而一个等价类是用一个抽象状态表示,故抽象状态可以反映出原始模型状态之间的关系。基于等价类划分的方法可以将原问题分解为若干个子问题并经过分别求解,划分后的问题状态空间远小于原问题状态空间,并且若某个子问题无解,则可以确定原问题无解。下面给出原始模型状态中的等价类定义。
定义3 对于一个基于原始模型的状态空间问题,若原始状态集合C依据谓词集合Φ划分成了若干个子状态集合{C1, C2,…,Ck},称Ci(1≤i≤k)是C中关于Φ的一个等价类,如果Ci满足如下条件:
1) Ci是C的一个子集;
2) Ci中每个状态都同时满足Φ所对应的一组布尔变量B的取值;
3) Ci中任意一个状态与jC中任意一个状态关于Φ所对应的布尔变量B取不同的值,其中i≠j,1≤i, j≤k。
一个原始模型的状态空间问题的一个等价类就是它的一个子问题,如果状态集合C中任意一个状态关于Φ所对应的布尔变量的取值均相同,即原始模型不能划分出一个以上的等价类,则称该状态空间问题为不变等价类,此时系统的状态不能进行等价类划分。
定理1 针对一个基于原始模型M的状态空间问题,如果可以通过谓词集合Φ划分为若干个等价类(即子问题),那么这些子问题可以单独求解,并且这些子问题解的组合就是原问题的解。
证明 由定义1,在抽象算子α运算过程中,系统M的状态集合C依据谓词集合Φ进行划分:{C1, C2,…,Ck},每个划分Ci( Ci⊆C)都是关于Φ的一个等价类,k为等价类的个数,即M的问题Q被分解成若干个子问题{q1, q2,…,qk}。设Ci中的状态c1和Cj中的状态c2关于谓词Φ集合布尔变量B的取值分别为和,根据定义3,≠,即表示一个等价类中的任意状态对应的布尔变量的真值不会影响到另一个等价类中任意一个状态对应的布尔变量的真值,那么每个子问题就可以在抽象模型上单独进行求解。在求得每个子问题解的基础上,根据定义2,抽象模型中各个子问题,可以通过精化算子γ映射到原始模型,依据谓词抽象的性质,在抽象模型中成立的性质,在原始模型中也同样成立,故在抽象模型中所求得的每个子问题的解s,同样也是原始模型中原问题的解,由于在子问题求解过程中,不同等价类中的状态之间关于布尔变量B的取值之间不会产生冲突,所以这些子问题的解的组合〈s1, s2,…,sn〉 就是原问题的解。 证毕
定理1表明,一个基于原始模型的状态空间的测试用例生成问题,可以依据谓词抽象操作将状态空间划分为若干个子问题并单独求解,若每个子问题都有解,则原问题也有解。经谓词抽象后,抽象模型拥有较少的状态空间及状态迁移关系,此时对每个等价类(子问题)生成约简的测试用例,最后将各个等价类所生成的测试用例集组合起来,就得到原始模型的约简测试用例集。
4 测试用例约简生成方法
通过对原始模型进行谓词抽象处理,得到约简的抽象模型,它包含若干原始模型状态集合上的等价类。在生成测试用例之前,首先需要获得抽象模型中的状态迁移集合,作为测试用例生成的基础,然后对每一个等价类中的状态集合,生成针对原始系统模型待验证性质的测试用例,最后依据等价类划分问题求解的性质,得到针对原始模型的约简测试用例。
4.1 抽象模型状态迁移生成算法
基于谓词的抽象模型的状态取决于所使用的谓词集合,状态迁移关系的复杂程度对测试用例的构造有直接关系,故需要生成抽象状态的迁移关系,下面给出系统模型M迁移关系的定义及其性质。
定义4 对于一个原始模型的状态空间集合C及其状态迁移集合RC,如果有c1∈C, c2∈C ,并且(c1→c2)∈RC ,则称c1和c2之间存在直接迁移关系。
定义5 对于一个原始模型的状态空间集合C及其状态迁移集合RC,如果有c1, c2, c3∈C,并且c1和c2之间、c2和c3之间均存在直接迁移关系,则称c1和c3之间存在间接迁移关系。
定义6 直接迁移和间接迁移统称为迁移关系。
迁移关系反映出系统状态之间的转换关系以及状态的可达情况,并能够指导系统状态的等价关系的构建。下面给出迁移关系的性质。
性质1 迁移关系具有传递性,即如果1c和2c之间、2c和3c之间均存在迁移关系,则1c和3c之间存在迁移关系。
原始模型迁移关系集合RC与抽象模型迁移关系集合RA的关系是:设与初始状态φ所关联的抽象状态是A( B1, B2,…,Bn),φ对应的原始状态迁移关系记为,其中Rφ⊆RC,Rφ是原始状态φ对应的原始模型状态迁移关系,则与Tj关联的抽象模型状态迁移关系通过如下表达式确定[10]:

其中,pj是Tj的进行语义操作的决定条件,即当前状态若满足pj,才存在迁移关系。在抽象迁移关系中,若成立,那么(A( B1, B2,…,Bn))=false,即抽象状态A( B1, B2,…,Bn)在中无后继状态。表示在迁移关系Tj下,当前状态的后继状态。若post[ Tj]成立,则ci的值为Bi;若post[ Tj](A(|))↦¬φi成立,则ci的值为¬Bi,若均不成立,则ci的值为true。
在定义了初始状态集合IC、初始状态迁移关系集合RC的原始模型后,就可以使用抽象算子α'和求出抽象模型。抽象模型的初始状态集合为IA,抽象状态迁移关系集合为RA。算法1给出了抽象迁移关系集合RA的求解过程。
算法1 抽象模型的状态迁移关系生成算法。
输入:谓词集合Φ、原始模型的初始状态集合IC,状态迁移关系集合RC。
输出:相对于谓词集合Φ的抽象模型A的状态迁移集合。
1) α' (Φ):=∧{Bi|Φ↦φi,1≤i≤n}; //初始化抽象算子α'
2) Ainit:=α'(IC);//初始化A的初始状态集合
3) Arest:=Ainit; //初始化未处理的抽象状态
4) Atran:=null; //初始化状态迁移关系
5) while(Arest不为空)
6) 从Arest中取出一个抽象状态A';
9) Atran:=Atran+A'tran;//更新Atran集合
10) Arest:=Arest-{A '};//更新Arest集合
11) end while
12) returnAtran;
4.2 基于状态约简的测试用例生成算法
测试用例集的约简基于模型系统状态迁移的约简,原始模型状态集合依据谓词集合Φ经算法1得到抽象状态迁移集合,由于每个抽象状态对应一个等价类,故以每一个等价类中的状态迁移集合为研究对象,通过谓词抽象自动验证工具对原始模型所具有的性质进行验证,若不满足该性质,工具可以自动返回不满足该性质的程序执行路径,并以此生成针对每个等价类的测试用例集。依据定理1,把抽象状态中每个等价类的测试用例组合起来,就可以得到原始模型的约简测试用例。
本文的测试用例约简生成方法首先针对每个等价类所生成约简的测试用例。对于测试用例ti和tj,它们之间存在如下关系。
1) 包含关系:若ti∩tj=ti,则ti包含于tj,记为ti⊆tj,它表明ti对应的状态迁移集合包含在tj对应的状态迁移集合中。
2) 相交关系:若ti∩tj≠∅,则ti与tj之间存在交集,记为ti⊕tj,它表明ti和tj有公共的状态迁移关系。
3) 独立关系:若ti∩tj=∅,则ti与tj相互独立,记为ti<>tj,即ti和tj没有公共的状态迁移集合。
其中包含关系是相交关系ti-ti∩tj≠∅的特例。在测试用例约简生成过程中,可以根据以上3种状态关系对每个等价类中的测试用例集进行约简,显然包含关系和相交关系可以约简,而独立关系不能进行约简。其约简规则如下。
若ti⊆tj,由于ti对应的状态迁移集合包含在tj对应的状态迁移集合之中,故约简后的结果是ti。
若ti⊕tj,由于ti和tj之间存在部分重合关系,将ti和tj对应的测试用例重合的部分作为约简后的结果,即保留ti∩tj。
若ti<>tj,此时ti和tj之间没有公共的迁移状态,此时无法进行约简操作。
在生成测试用例的时候,由于每个等价类可能对应于原始模型中多个状态,如果不能生成一条测试用例满足该等价类中的各种状态,此时需要将测试用例依据以上3种关系进行约简,这样可以在满足原始模型状态迁移关系的同时,能够生成规模较小的测试用例集。
本文是针对原始模型待验证的性质集合P来生成测试用例的,故需要对这些性质进行形式化描述,作为谓词抽象自动验证工具的输入参数。这里的性质集合P就是谓词抽象过程中待验证的原始模型所具有的性质集合。
算法2 每个等价类的测试用例约简生成算法。
输入:经形式化描述的待验证的性质集合P。
输出:约简的测试用例集RT。
1) :RTnull=;//初始化约简的测试用例集
2) :STnull=;//初始化所有测试用例所包含的状态迁移集合
3) while(P不为空)
4) 从P中选择一条待验证的性质p;
5) P:=P-{p};//从集合P中删除p
6) T:=genTestCase( p);//生成针对p的测试用例T
7) foreachpi∈P( pi≠p)do
8) satisfy( T, pi);//验证T是否满足pi
9) end
10) E:=tran( T)∩ST;//生成已包含在之前测试用例所覆盖的状态
11) if getSubSuite( E)不为空then
13) foreachT'∈getSubSuite( E)except TLdo
14) ':'TTE=-;//更新'T集合
15) end
16) end
17) ST:=ST+tran( T);//更新ST集合
18) :RTRTT=+;//更新RT集合
19) end while
算法2依据每个等价类中的状态之间的关系,针对原始模型待验证的性质,调用谓词抽象自动验证工具生成对应的测试用例,并对生成的测试用例集进行约简。经前面的分析可知,每一个等价类中只有包含关系和相交关系的测试用例可以进行约简。算法首先从待验证的性质集合中选取一条性质,通过函数genTestCase( p)调用谓词抽象自动验证工具生成针对性质p的测试用例T,并验证T是否还可以满足性质集合P中其他的性质,若能够满足,则从P删除对应的性质。函数satisfy( T, pi)用来验证测试用例是否满足某些性质。函数tran( T)记录测试用例所包含的状态迁移集合,它与ST集合求交集,得出已包含在之前测试用例所覆盖的状态E。函数getSubSuite( E)生成包含状态E的所有测试用例集,并从中选择包含状态数最多的测试用例TL,同时删除其他用例中包含E的部分,并更新ST和RT集合,直到P集合为空。
图1显示了对测试用例进行约简过程,其中图1(a)表示3个测试用例:t1=〈s0, s1〉,t2=〈s0, s1, s2〉,t3=〈s0, s1, s2, s3〉,它们分别显示各自所包含的状态以及状态迁移关系,依据本节引入的约简规则,使用算法2可以生成约简后的测试用例t,如图1(b)所示,该测试用例t可以替代t1, t2, t3,以减少系统依据测试用例进行测试环境初始化所带来的开销。

图1 测试用例约简过程
算法复杂性方面,由于算法2是一种基于线性搜索的测试用例约简方法,对于每条性质所生成的测试用例都需要对P中其他性质进行检验,其时间复杂度为O( k),其中k=|P|,故整个算法的时间复杂度为O( k2),相对于贪心算法,算法2的时间复杂度较低,效率也更高。需要说明的是,通过谓词抽象自动验证工具,该算法可以同时得到P中不能针对谓词集合Φ生成测试用例的性质,这些性质的来源可能是谓词抽象自动验证工具无法为其生成测试用例,也可能是谓词集合需要进一步精化再来生成该性质的测试用例。
对于每个等价类生成的约简测试用例集{RT1, RT2,…,RTk},其中k=|IA|,把RT1, RT2,…,RTk依据算法1得到的抽象状态迁移关系RA进行连接就可以得到对应于原始模型系统的测试用例集,该集合就是最后约简的测试用例集。RT1, RT2,…,RTk的连接过程是:设抽象模型的迁移关系为I1→I2→…→Ik,其中k=|IA|,则RT1, RT2,…,RTk依据抽象模型迁移关系构建序列:RT1→RT2→…→RTk,对于RT1→RT2,把RT1中的每条测试用例与RT2中的每条测试用例依据原始状态迁移关系集合RC进行连接,依次拓展到RTk。
图2表示2个测试用例的连接过程,设t1∈RT1, t2∈RT2,(s3→s5)∈RC, 测 试 用 例t1=s0, s2, s3,t2=s5, s6, s7,将t1和t2连接所得到的测试用例t=s0, s2, s3, s5, s6, s7。

图2 不同等价类的测试用例连接过程
4.3 状态约简实例分析
本节通过一个实例,对基于谓词抽象方法的原始模型状态约简过程进行描述。对于一个原始模型,设其原始状态集合C={si|si=i,0≤i ≤14},状态迁移关系集合RC为
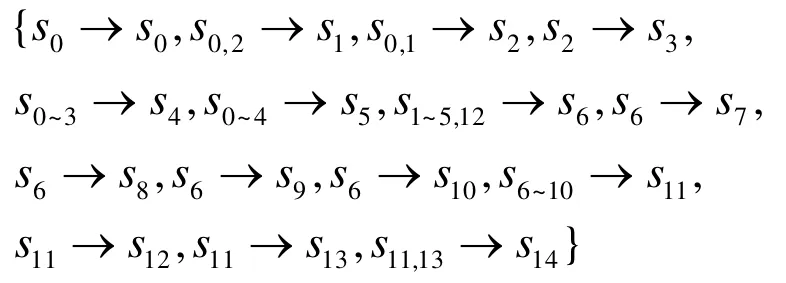
图3上部分反映原始状态及状态间的迁移关系。谓词集合Φ为{φ1, φ2, φ3, φ4},其中φ1=si<5,φ2=si<7,φ3=si>10,φ4=si>12。与φ1,φ2, φ3,φ4关联的布尔变量是B1, B2, B3, B4,按照算法1,各状态相对于谓词集合Φ的抽象状态为


此时,抽象模型对应的抽象状态集合A为
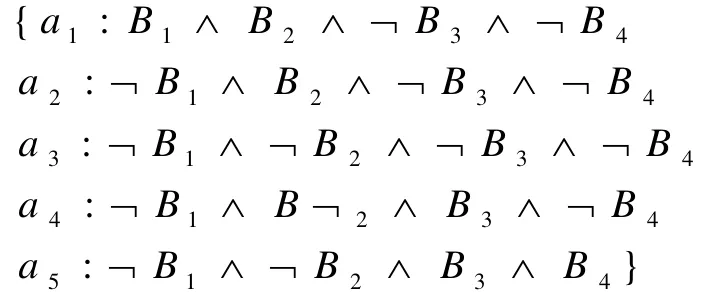
抽象状态所对应的迁移关系集合:
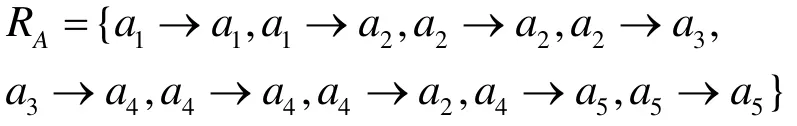
图3的下部分显示了基于谓词抽象所得到的约简模型及抽象状态之间的迁移关系。通过对比,原始模型的状态经谓词抽象操作后被划分成了5个等价类,每个等价类包含多个原始模型的状态,抽象模型的状态数量和状态间的迁移关系的复杂程度均明显减少。约简的状态模型作为测试用例生成的前期处理,有助于生成较小规模的测试用例集。
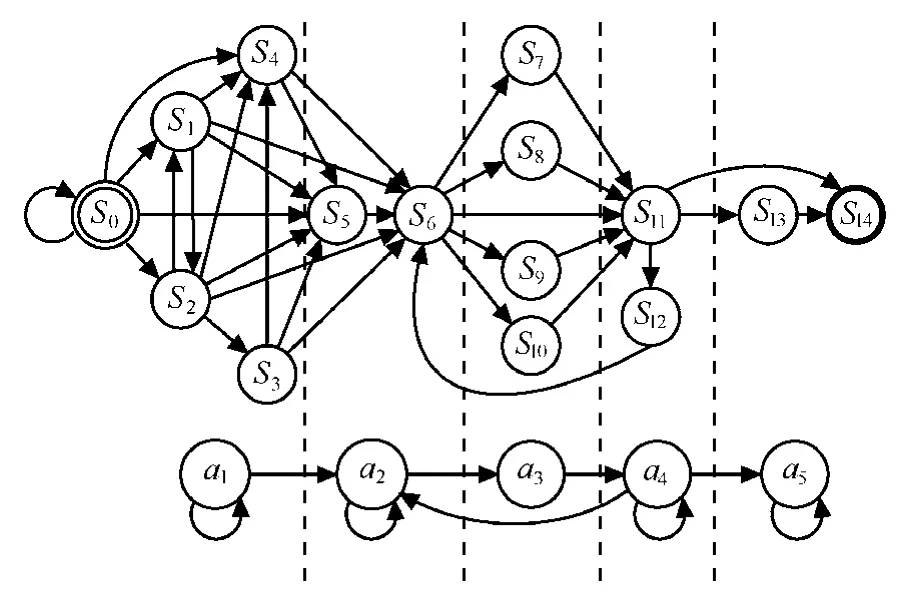
图3 谓词抽象处理前后系统状态的迁移关系
5 测试用例约简生成的仿真实验
为了验证本文提出的方法的有效性,进行了一系列仿真实验,把现有的几种典型的测试用例约简方法和本文所提出的方法进行对比。实验环境是2.6.24-24内核的Ubuntu 8.10版Linux系统,2.2GHz的处理器,2GB的物理内存空间。
仿真实验的方案是:构建原始模型的程序控制流图(CFG),根据CFG设定初始的谓词集合;为了验证原始模型是否所具有待验证的性质,使用BLAST工具[11]构建基于初始谓词的抽象模型,并使用定理证明器Simplify[12]对抽象状态迁移关系进行求解;在获得抽象模型的状态迁移关系后,使用本文的算法生成约简的测试用例;由于测试用例约简问题是NP-C问题,一般采用启发式算法获取近似解,为了对比本文方法的性能,分别使用贪心算法、启发式算法(HGS算法)和GRE算法这3种典型的测试用例约简算法进行对比实验,并分析实验结果。
仿真实验过程中涉及到的参数有:程序源代码的长度L,程序CFG图中状态个数S,约简模型中状态个数S’,基于本文方法生成的测试用例个数T,通过分析测试对象程序的调用图(call graph),分别使用N-live和N-dead表示语法上可达与不可达的位置个数,N-prdc表示每个测试对象为满足待验证的性质所产生的谓词个数,每一次实验就是对一组参数(S, S’, N-prdc ,T)的赋值。
测试对象为kbfiltr、floppy、cdaudio及ping,其中,前3个分别是关于键盘、软驱和音频的设备驱动程序,ping是一个网络监测工具。仿真实验中待验证的性质为程序的状态覆盖,通过生成约简的测试用例集以满足该性质。实验结果如表1所示,其中T-G、T-HGS、T-GRE分别为对测试对象使用贪心算法、启发式算法和GRE算法所生成的测试用例个数。
实验结果显示,贪心算法、HGS算法和GRE算法在测试用例约简生成方面的性能大致相当,也符合文献[13]对这几种算法比较的结果。由于HGS算法和GRE算法在计算过程中,可能会调用贪心算法,故在贪心算法计算过程中通常生成比HGS算法和GRE算法略大的测试用例集。与现有的几种算法相比,基于谓词抽象的测试用例约简生成算法由于对原始模型的状态依据谓词进行划分,能够得到约简的抽象模型及其状态间的迁移关系,表1中T数值表明本文的方法可以在满足程序待验证的性质的基础上,生成数量较少的测试用例集。Ratio显示本文的方法相对于其他3种方法关于测试用例个数的最大约简比例,对于规模较小的kbfiltr和ping,测试用例数量的约简比例较高;而对于规模较大的floppy和cdaudio,则约简比例相对较低,其原因是随着程序规模的增大,系统的状态空间和迁移关系更加复杂,谓词的选取和精化过程的开销也随之增大,等价类中测试用例之间可约简的程度也会同时降低,故会生成较多的测试用例。
在程序执行时间上,本文方法在系统模型状态约简阶段和测试用例生成阶段的时间复杂度均为O( k2),故本文方法的总时间复杂度为O( k2),前文提到贪心算法、HGS算法和GRE算法这3种典型的启发式方法的时间复杂度分别为O( mn·min(m, n))、O( m( m+n) k)和O(min(m, n)( m+n2k)),相比之下本文算法有更低的时间复杂度。文献[13]指出在精确性方面,现有的几种启发式方法已被证实任何一种算法都不比其他算法优越,故本文选择时间复杂度相对较低且易于实施的贪心算法与本文方法进行对比。在测试对象选取上,选择规模最大的cdaudio程序和规模较小的ping程序。由于前文提到的3种启发式算法的时间复杂度均为最坏情况下复杂度,故在模拟实验过程中,该3种启发式算法的时间开销比本文方法的略大,通过图4可以看出,程序规模越大,本文算法在时间开销上提高的效果越明显。
在实验过程中,BLAST所生成的抽象状态模型本质上是一个有限状态自动机(FSA),由于FSA无法描述带有递归调用的程序,故在实验前对程序中含有递归调用的部分进行预处理,使之不反映到程序的控制流图中。在测试用例生成过程中,谓词抽象自动验证工具可以根据反例的抽象精化功能,不断对初始谓词集合进行完善,同时还可以验证原始模型不能满足的性质,以利于对程序所具有的性质的研究。

表1 实验结果

图4 算法的时间开销对比
6 结束语
测试用例的质量和数量决定测试的成本和有效性,但大规模软件系统往往存在状态空间爆炸的问题,故难以生成精简、高效的测试用例集,从而影响对软件系统所具有性质的验证。谓词抽象技术可以有效地减少系统的状态迁移的数量,以此作为测试用例集约简生成的基础。本文提出一种基于谓词抽象的测试用例约简生成算法,以系统的状态迁移关系作为研究目标,通过谓词集合将原始系统的初始状态进行等价类划分,并使用谓词抽象自动验证工具的反例引导功能,生成满足给定性质的测试用例。实验数据表明,相对于其他几种典型的测试用例约简方法,本文的方法可以在较短时间内生成数量较少的测试用例集。
然而本文方法还存在改进的空间,例如对于程序中存在的递归调用语句,本文的方法还不能处理,这将限制其使用范围,将来的工作中,可以考虑使用支持递归调用的谓词抽象验证工具来改进本文中的方法;另外,对于具有可信特征属性需求的系统,根据文献[14]的观点:可信≈可靠+安全,可以对谓词的属性表示方法进行扩展,使本文的方法在具有可靠、安全等非功能特征属性的系统中也能够生成约简的测试用例。
[1] HARROLD M J, GUPTA R, SOFFA M L. A methodology for controlling the size of a test suite[J]. ACM Transactions of Software Engineering and Methodology, 1993, 2(3):270-285.
[2] 屈婉霞, 李暾, 郭阳等. 谓词抽象技术研究[J]. 软件学报, 2008,19(1): 27-38.QU W X, LI T, GUO Y, et al. Advances in predicate abstraction[J].Journal of Software, 2008, 19(1): 27-38.
[3] HONG H S, CHA S D, LEE I, et al. Data flow testing as model checking[A]. Proceedings of the 25th International Conference on Software Engineering[C]. Portland, 2003, 232-243.
[4] CHVATAL V. A greedy heuristic for the set-covering problem[J].Mathematics of Operations Research, 1979, 4(3): 233-235.
[5] CHEN T Y, LAU M F. On the completeness of a test suite reduction strategy[J]. The Computer Journal, 1999, 42(5): 430-440.
[6] LEE J G, CHUNG C G. An optimal representative set selection method[J]. Information and Software Technology, 2000, 42(21):17-25.
[7] 章晓芳, 徐宝文, 聂长海等. 一种基于测试需求约简的测试用例集优化方法[J]. 软件学报, 2007, 18(4): 821-831.ZHANG X F, XU B W, NIE C H, et al. An approach for optimizing test suite based on testing requirement reduction[J]. Journal of Software, 2007, 18(4): 821-831.
[8] 程亮, 张阳, 冯登国. 一种基于安全状态转移的简并测试集生成方法[J]. 软件学报,2010,21(3): 539-547.CHENG L, ZHANG Y, FENG D G. Approach of degenerate test set generation based on secure state transition[J]. Journal of Software,2010, 21(3): 539-547.
[9] 徐明迪, 张焕国, 严飞. 基于标记变迁系统的可信计算平台信任链测试[J]. 计算机学报, 2009, 32(4): 635-645.XU M D, ZHANG H G, YAN F. Testing on trust chain of trusted computing platform based on labeled transition system[J]. Chinese Journal of Computers, 2009, 32(4): 635-645.
[10] SUSANNE G, HASSEN S. Construction of abstract state graphs with PVS[A]. Proceedings of the 9th International Conference on Computer Aided Verification[C]. Berlin, 1997. 72-83.
[11] HENZINGER T A, JHALA R, MAJUMDAR R. Lazy abstraction[A].ACM Symposium on Principles of Programming Language[C]. Oregon, 2002. 58-70.
[12] DETLEFS D, NELSON G, SAXE J B. Simplify: a theorem prover for program checking[J]. Journal of the ACM, 2005, 52(3): 365-473.
[13] CHEN T Y, LAU M F. A simulation study on some heuristics for test suite reduction[J]. Information and Software Technology, 1998,40(13): 777-787.
[14] 沈昌祥,张焕国,冯登国等. 信息安全综述[J]. 中国科学E辑, 2007,37(2): 129-150.SHEN C X, ZHANG H G, FENG D G, et al. Survey of information security[J]. Science in China, Series E, Information Sciences, 2007,37(2): 129-150.
