基于凸组合的同步长最大均方权值偏差自适应滤波算法
2012-08-10芮国胜苗俊张洋王林
芮国胜,苗俊,张洋,王林
(1.海军航空工程学院 电子信息工程系,山东 烟台 264001;2.海军航空工程学院 研究生管理大队,山东 烟台 264001)
1 引言
系数比例自适应(PNLMS, proportionate NLMS)算法[1~3]是近年来发展起来的一种快速收敛算法。该算法在处理稀疏特性信道时具有较快的收敛速度,其收敛性能优于传统的NLMS滤波器,但在处理非稀疏特性信道时,与NLMS算法相比其收敛速度较慢。为此,文献[4]提出了一种IPNLMS算法改善了这种情况下的收敛速度,但它需要预先确定一个决定算法的行为参数,给实际应用带来不便。当信道冲激响应为时变时(如电话会议中的声学回声消除器[2],微波通信信道的均衡等),IPNLMS算法性能急剧下降,其实用性大打折扣。针对这一情况,本文基于滤波器的凸组合的思想[5~7],提出了一种同步长的NLMS和PNLMS凸组合算法。该算法是基于每步迭代中,使得均方权值偏差(MSD, mean square deviation)的下降达到最大,提高了算法的收敛速度及其在时变信道环境下的跟踪性能。为了保证系统的稳态性能、减少系统的失调,NLMS滤波器步长应与PNLMS滤波器步长保持一致。仿真结果表明:该算法具有良好的收敛性能和跟踪性能,具有实用价值。
2 组合滤波器算法
组合滤波器的原理如图1所示。

图1 组合滤波器的原理
图1中,ω1(n)、ω2(n)、ω0(n)分别为PNLMS滤波器、NLMS滤波器和未知系统的权向量;y1(n)、y2(n)分别为2个滤波器的输出;e1(n)、e2(n)分别为2个滤波器产生的误差;λ(n)为组合算法的组合系数;y(n)为整个滤波器的等效输出;e(n)为滤波器等效误差,滤波器的长度为L。
算法采用2个同步长的PNLMS滤波器、NLMS滤波器的并联凸组合形式,其核心思想在于:PNLMS滤波器能保证处理稀疏冲激响应时的快速特性;而另一个NLMS滤波器则保证处理非稀疏冲激响应时的优良特性,滤波器组可根据均方权值偏差MSD大小设定不同的组合参数 λ(n)的值,并以此调整2个滤波器的权重,使其根据信道环境变化发挥不同滤波器的优势。
组合算法采用PNLMS滤波器和NLMS滤波器凸组合的方式得到等价权值向量:
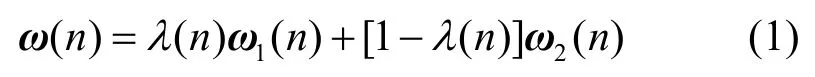
其中,组合系数λ(n)∈(0,1),并定义其取值函数为
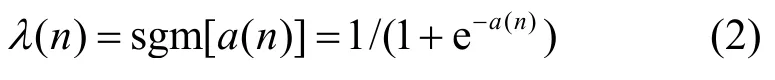
由此可得等价输出项与误差项的表达式:

组合系数λ(n)中的参数a(n)通过使整个自适应滤波器的均方权值偏差MSD下降最大为自适应准则,则a(n)的更新式(见附录1)为
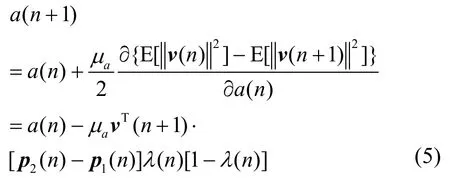
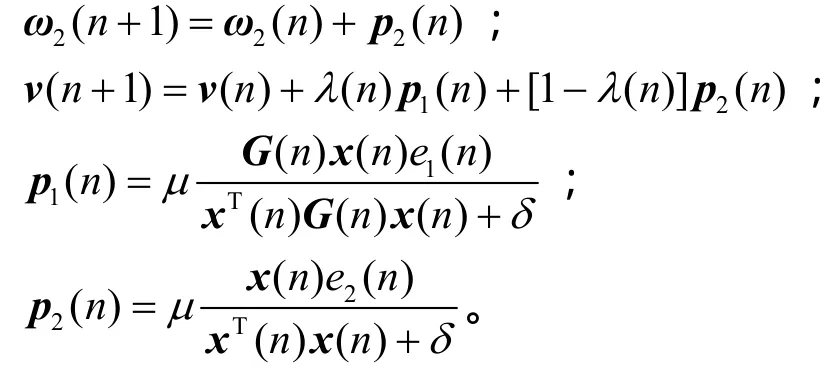
需要注意的是,a( n)∈[-a+,a+],以保证λ(n )∈[1-λ+,λ+],其中,λ+=sgm(a+)是接近于1的常数,即
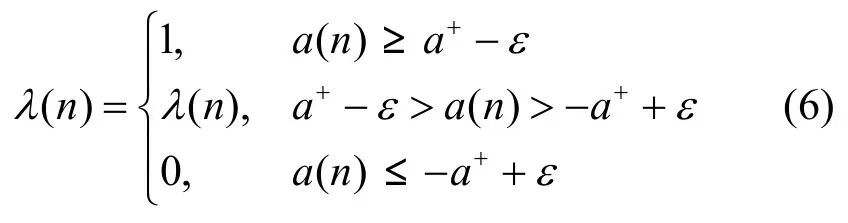
其中,ε为一个很小的正常数。
3 组合滤波器算法的均方性能分析
在进行算法性能分析前,首先提出如下假设[5]。
1) 期望响应d(n)与输入向量x(n)间符合如下线性衰减模型:
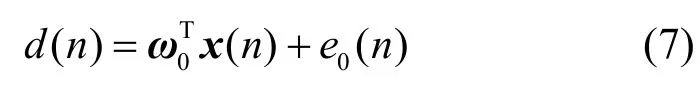
其中,ω0为长度为M的未知权向量;e0(n)为方差为的独立建模观测噪声。
2) 初始权向量ω1(0)、ω2(0)与初始参数a(0)对于任意n值独立于{x(n),d(n),e0(n)}。
3) E[x(n)]=0,E[x(n)xT(n)]=R,E[d(n)]=0,E[e0(n)]=0。
4) 步长µ和e(n),x(n),v(n)均相互独立。
5) 输入信号是平稳随机信号,║x(n)║2可用来估计。
为了讨论方便,现分别对单个滤波器与组合后的滤波器定义如下符号与附加参数值。
1) 滤波器的权向量误差项为
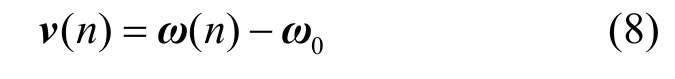
2) 先验误差项为

3) 后验误差项为
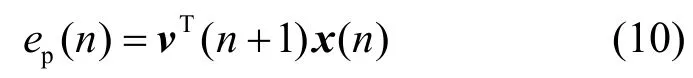
滤波器的性能通常用额外均方误差(EMSE)来衡量,将它定义为滤波器在工作过程中除最小均方误差外的额外误差项。分析算法的稳定性能时,通常假设学习迭代次数n取其极限值∞,由于误差项e(n)满足如下表达式:
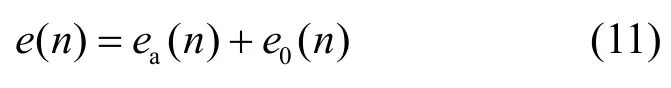
因此,各滤波器的EMSE可由下式得到:
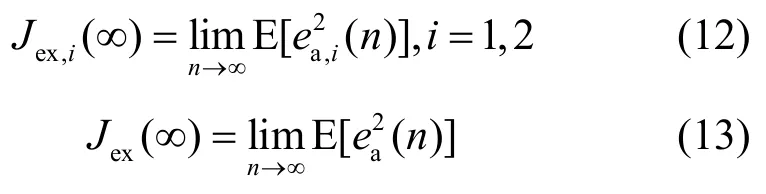
同时为分析凸组合后系统性能,定义基于先验误差项的交叉EMSE表达式如式(14)所示:
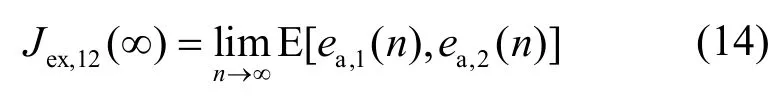
由定义式(14)与Cauchy-Schwartz不等式可得出如下结论:交叉项EMSE不会同时高于单个滤波器的EMSE。即
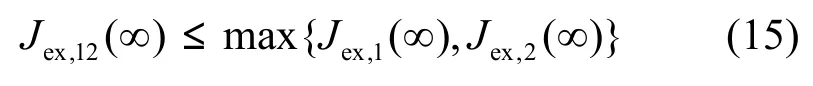
3.1 组合滤波器的稳态EMSE
组合滤波器的误差项e(n),可由式(3)减去d(n)得到:
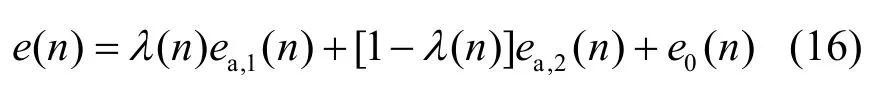
其中,ei=d(n)–yi(n)。同理,得到组合滤波器的先验误差项ea(n):
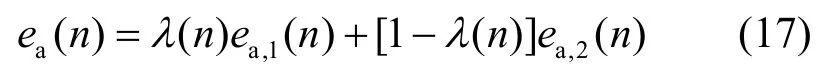
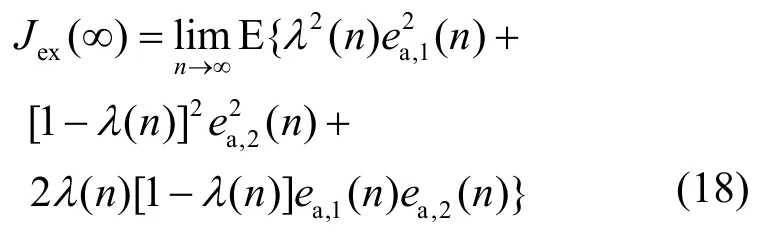
组合参数λ(n)和局部滤波器的先验误差交叉项的出现,以及更新参数a(n)在λ(n)中是非线性的,使得式(18)难以准确估计。但存在如下2种情况,使得Jex(∞)可被简化估计。


由此不难得出如下结论,不管在什么样的条件,检测稳态值E{a(n)}是否趋于某个常数是很重要的,接下来将对组合参数的稳态性能进行分析。
3.2 组合参数的稳态性能分析
组合参数a(n)的更新式为式(5),对等式的两边取期望:
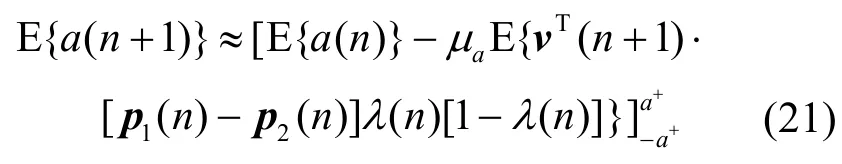
需要注意的是,对式(5)取期望并对算子进行取值限定,因而是一个近似式。这种近似是合理的,因为a(n)在被限定之前,大于a+或小于-a+是有可能的,为了使a(n)更加接近±a+,缩小因子λ(n)[1-λ(n)]就显得尤为重要。
将式(21)转化为组合参数的先验误差形式(见附录2):
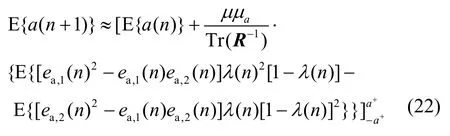
假设:稳态时λ(n)独立于2个滤波器的先验误差,则当n→∞,由式(22)得到:

其中,ΔJi=Jex,i(∞)-Jex,12(∞),i=1,2表示单个滤波器的EMSE与交叉EMSE的相差程度。
从式(23)中可以看出,E{a(n)}的极限值依赖于ΔJi, i=1,2的值。由式(14)可知这2个值不可能同时都小于零,考虑以下这3种情况:
情况1 如果Jex,1(∞)≤Jex,12(∞)≤Jex,2(∞),那么ΔJ1≤0,ΔJ2≥0。因为λ(n)∈[1-λ+,λ+],那么E{λ(n)[1-λ(n )]2}和E{λ(n)2[1-λ(n)]}均小于λ+(1-λ+)2。则可得:
当n→∞时,
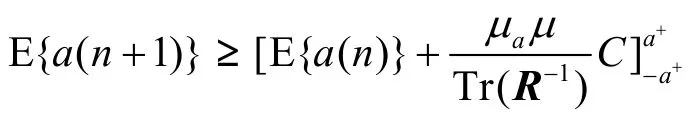
其中,C =λ+(1-λ+)2(ΔJ2-ΔJ1)为一正常数。因此,对于式(21)的唯一有效极限点为a(∞)=a+,则有
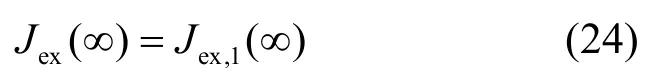
情况2 如果Jex,1(∞)≥Jex,12(∞)≥Jex,2(∞),那么ΔJ1≥0,ΔJ2≤0。同理得:
当n→∞时,
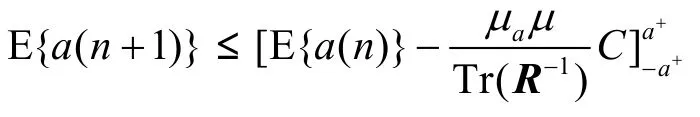
其中,C =λ+(1-λ+)2(ΔJ1-ΔJ2)为一正常数。因此,对于式(21)的唯一有效极限点为a(∞)=-a+,则有
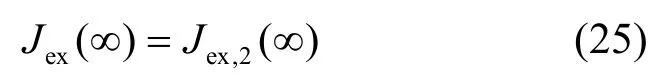
情况3 如果Jex,12(∞)<Jex,i(∞),i =1,2,则有ΔJi>0,i =1,2。式(21)的极限点可以通过式(26)描述。
当n→∞时,
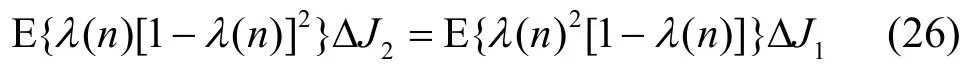

由式(27)得:

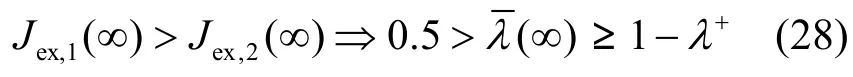
由式(18),得到:

将式(27)未加限定代入式(29),得
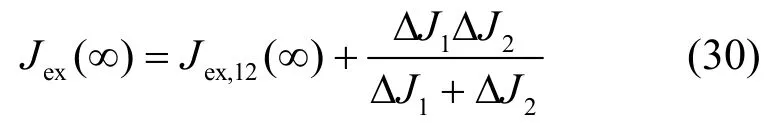
又因为1-λ+<(∞)<λ+<1,ΔJi=Jex,i(∞)-Jex,12(∞),所以就有
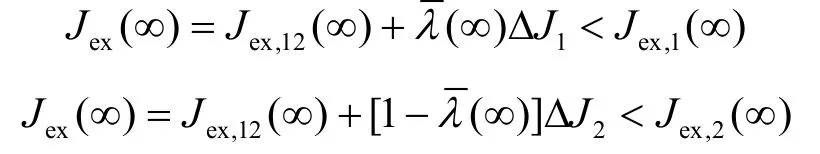
即有Jex(∞)<min{Jex,1(∞),Jex,2(∞)}。
4 计算复杂度分析
以每次迭代时的乘法操作数来衡量组合算法的计算复杂度。依照式(22)可知,更新a(n)需要13个乘法操作,依照式(5)、式(16)的备注式知,更新ea1(n)需要2L2+3L+3个乘法操作,更新ea2(n)需要3L+3个乘法操作。实际上根据Sigmoid函数计算λ还需要一些额外的计算量,但可以用查表的方式实现[8]。因此,该组合算法的计算复杂度为2L2+6L+19。
5 计算机模拟实验
5.1 仿真设置
为了进一步验证所提出组合算法的收敛性能与跟踪性能,现将组合算法与NLMS算法、PNLMS算法和IPNLMS算法应用于信道均衡的仿真分析,并分别对这4种算法进行N次独立仿真实验,求取统计平均值。同时,为能够客观比较系统失调等性能参数,4种算法的参数均选用文献[4,9,10]中讨论过的相对最优参数,见表1。
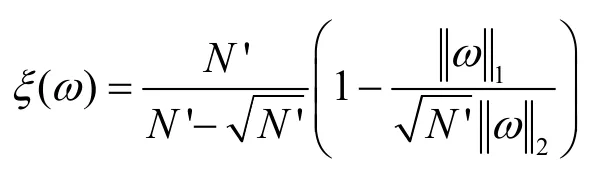
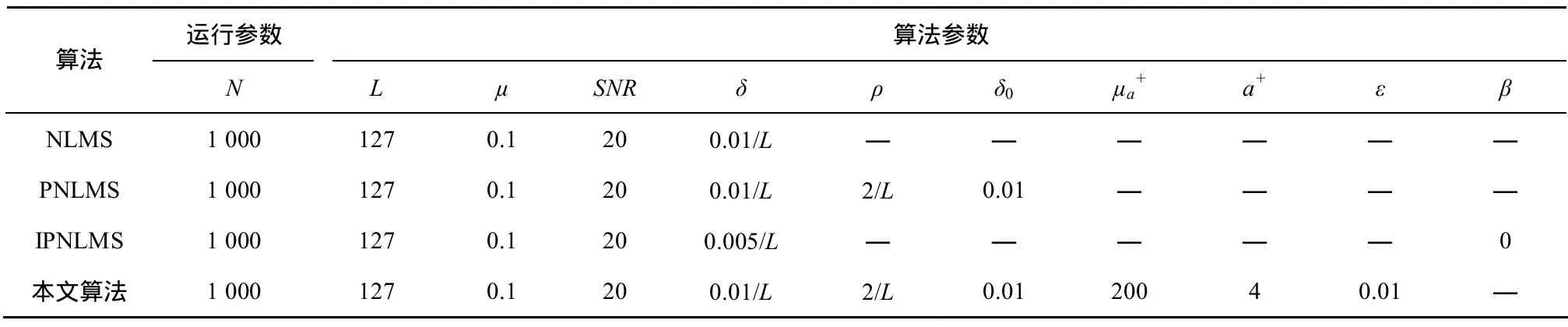
表1 模拟实验参数设置
根据仿真需求定义向量ω的稀疏度ξ(ω)[1]:其中,N'是向量ω的长度,║ω║1表示向量的L1范数,║ω║2表示向量的L2范数。需要说明的是,本文根据稀疏度ξ的大小将信道特性分为3类:稀疏信道(ξ≥0.6),非稀疏信道(ξ<0.2)和模糊态信道(0.2≤ξ<0.6)[11]。
5.2 仿真结论
第一组仿真实验比较了稀疏信道特性(稀疏度ξ=0.927)时,4种算法的初始收敛速度。仿真采用PN码作为输入的训练序列,干扰信号是与输入信号不相关的白噪声,仿真结果如图 2所示。从图2中可以看到,在相同的全局步长参数条件下,PNLMS算法比 NLMS、IPNLMS算法收敛速度有很大改善,同时PNLMS的稳态失调有所改善。此时,所提及组合算法与PNLMS算法有相同的初始收敛速度,同时它们的稳态失调也相近。

图2 (信道稀疏)4种算法的初始收敛速度比较
第二组仿真实验比较了非稀疏信道特性(稀疏度ξ=0.102)时,4种算法的初始收敛速度。信道特性为非稀疏,其他仿真条件与第一组仿真相同,仿真结果如图3所示。从图3中可以看到,在相同的全局步长参数条件下,NLMS的收敛速度优于PNLMS、IPNLMS算法,同时稳态失调也有所改善。此时,所提及组合算法与NLMS有相同的初始收敛速度,同时它们的稳态失调也相近。
第三组仿真实验比较了模糊态信道特性(稀疏度ξ=0.443)时,4种算法的初始收敛速度。信道特性为介于稀疏与非稀疏的模糊态,其他仿真条件与第一组仿真相同,仿真结果如图4所示。从图4中可以看到,在相同的全局步长参数条件下,起初PNLMS算法的收敛速度优于 NLMS、IPNLMS算法,迭代至450步左右,NLMS算法的收敛速度开始优于PNLMS算法直至稳态,在此过程中IPNLMS算法和所提及组合算法都表现出了较好的收敛速度和稳态失调度,尤其是所提及组合算法性能明显优于其他几种算法。由此得出结论,不论信道特性如何变化,所提及组合算法总能“智能”表现出比较适合信道均衡的自适应滤波算法。
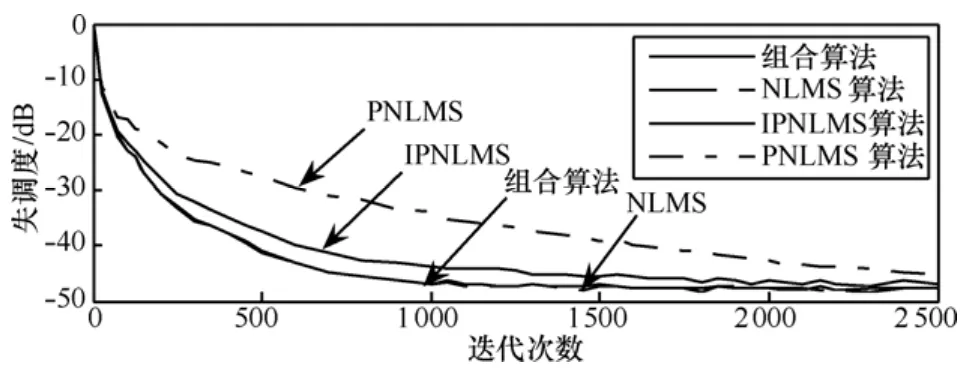
图3 (信道非稀疏)4种算法的初始收敛速度比较
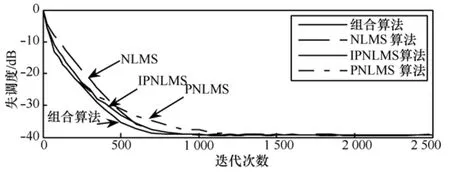
图4 (信道模糊态)相关算法的初始收敛速度比较
另外,为比较算法的跟踪性能,令信道模型参数在迭代进行至1 500步时同时发生变化,由模糊态转化为非稀疏状态,得到 NLMS算法、PNLMS算法、IPNLMS算法与组合算法的学习曲线,如图5所示。
从图 5可以看出,仿真前半部分(信道模糊态)收敛过程的初始阶段,组合算法和PNLMS算法的收敛速度明显快于NLMS、IPNLMS算法;在收敛过程进入稳态阶段后,组合算法又继承了NLMS、PNLMS和IPNLMS算法低稳态误差优点。仿真后半部分(信道非稀疏)收敛过程的初始阶段,组合算法和NLMS算法的收敛速度明显快于PNLMS算法;在收敛过程进入稳态阶段后又继承了NLMS、PNLMS和IPNLMS算法低稳态误差优点,在稳态性能上优于PNLMS。因为新算法对组合参数进行了限幅,这样极大地缩小了系统渐进稳态的过渡过程。同时在系统参数发生变化时,所提及组合算法也表现出较好的跟踪性能。
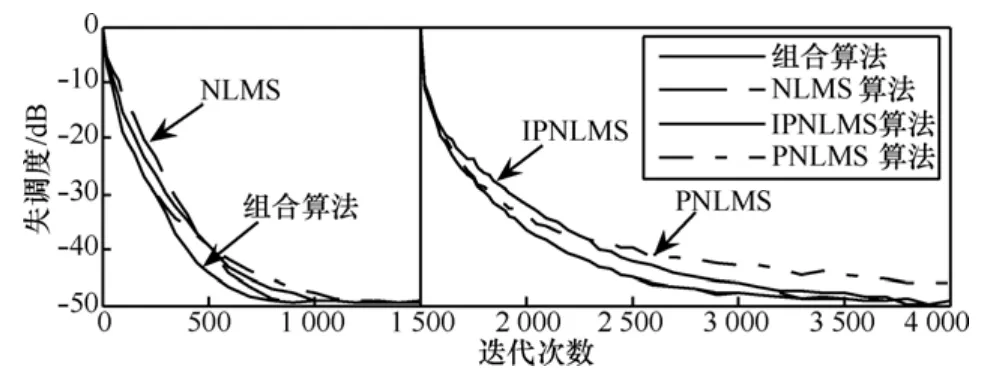
图5 4种算法的跟踪能力
6 结束语
同步长凸组合MMSD算法在凸组合思想的基础上,以最大均方权值偏差为准则,解决了时变环境的情况下,自适应滤波器的收敛速度及其跟踪性能差的问题。为了保证系统的稳态性能、减少系统的失调,NLMS滤波器步长应与PNLMS滤波器步长保持一致。理论推导证明和仿真结果验证了算法的收敛性能与稳态均方性能。
附录1
因为
v(n+1)=v(n)+λ(n)p1+[1-λ(n)]p2,则有

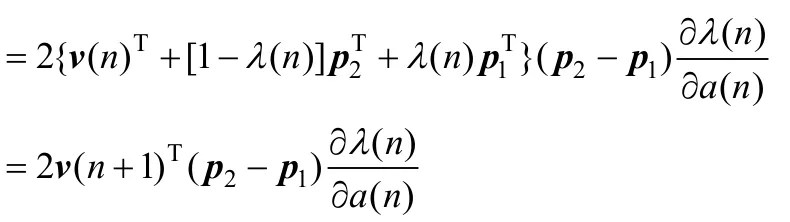
所以,
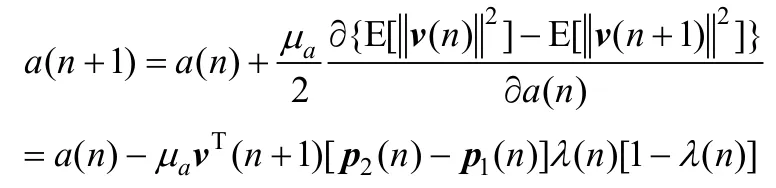
得证。
附录2
由式(21)到式(22)的推导:
[1] HUANG Y, BENESTY J, CHEN J. Sparse Adaptive Filters in Acoustic MIMO Signal Processing[M]. NJ, USA: Springer-Verlag, 2005.28-32.
[2] DUTTWEILER D L. Proportionate normalized least-mean-squares adaptation in echo cancellers[J]. IEEE Transactions on Speech Audio Processing, 2000, 8(5):508-518.
[3] MARTIN R K, SETHARES W A, WILLIAMSON R C. Exploiting sparsity in adaptive filters[J]. IEEE Transactions on Signal Processing,2006, 50(8):1883-1894.
[4] BENESTY J, GAY S L. An improved PNLMS algorithm[A]. Proceedings of IEEE International Conference on Acoustic, Speech and Signal Processing (ICASSP’02)[C]. Orlando, USA, 2007.1881-1884.
[5] ARENAS-GARCIA J, FIGUEIRAS-VIDAL A R, SAYED A H.Mean-square performance of a convex combination of two adaptive filters[J]. IEEE Transactions on Signal Processing, 2006, 54(3):1078-1090.
[6] ZHANG Y G, CHAMBERS J A. Convex combination of adaptive filters for a variable tap-length LMS algorithm[J]. IEEE Transactions on Signal Processing Letters, 2008, 13(10):628-631.
[7] KOZAT S S, ERDOGAN A T, SINGER A C. Steady-state MSE performance analysis of mixture approaches to adaptive filtering[J].IEEE Transactions on Signal Processing, 2010, 58(8): 4050-4063.
[8] ARENAS-GARCIA J, GOMEZ-VERDEJO V, FIGUEIRAS- VIDAL A R. New algorithms for improved adaptive convex combination of LMS transversal filters[J]. IEEE Transactions on Instrumentation Measurement, 2005, 54(6): 2239-2249.
[9] 于霞, 刘建昌, 李鸿儒. 一种变步长凸组合自适应滤波器及其均方性能分析[J]. 电子学报, 2010, 38(2):480-484.YU X, LIU J C, LI H R. A convex combination of variable step-size adaptive filter and its mean-square performance analysis[J]. Acta Electronica Sinica, 2010, 38(2):480-484.
[10] 刘立刚, Fukmoto Masahiro, 张世永. 一种变步长 Proportionate NLMS自适应滤波算法及其在网络回声消除中的应用[J]. 电子学报, 2010, 38(4):973-978.LIU L G, MASAHIRO F, ZHANG S Y. A variable step-size proportionate NLMS adaptive filtering algorithm and its application in network echo cancellation[J]. Acta Electronica Sinica, 2010, 38(4):973-978.
[11] LIU L G, MASAHIRO F, ZHANG S Y. A variable parameter improved proportionate normalized LMS algorithm[A]. IEEE Asian Pacific Conference on Circuits and Systems (APCCAS’08)[C]. Macau,China, 2008.201-204.
