基于粒子群优化的ad hoc网络最小能耗多播路由算法
2012-08-10朱晓建沈军
朱晓建,沈军
(1.东南大学 计算机科学与工程学院,江苏 南京 211189;2.东南大学 计算机网络和信息集成教育部重点实验室, 江苏 南京 211189)
1 引言
无线ad hoc网络由一组无线设备组成,在不需要使用网络基础设施的情况下,可以实现快速临时组网,具有广泛的应用。在无线ad hoc网络中,节点使用电池提供能量,而电池的能量十分有限,一旦电池的能量耗尽,节点将不能继续工作,网络将不再连通。因此,在无线ad hoc网络中,节能是一个核心问题,针对越来越多的多播应用,如何构造最小能耗多播树是一个重要问题。
文献[1]指出在无线ad hoc网络中无论使用全向天线还是使用有向天线,构造最小能耗多播树问题是一个NP难解问题,因此需要设计有效的启发式算法以求得较好的近似最优解。文献[2]提出了在使用全向天线的情况下构造最小能耗广播树的BIP(broadcast incremental power)算法和构造最小能耗多播树的MIP(multicast incremental power)算法,MIP算法首先利用BIP算法构造一棵广播树,然后对该广播树进行修剪得到多播树,未考虑不同的中继节点选择对构造多播树的影响。文献[3]提出了在使用有向天线的情况下构造最小能耗广播树的D-BIP(directional BIP)算法和构造最小能耗多播树的D-MIP(directional MIP)算法,与MIP算法基于BIP算法类似,D-MIP算法是基于D-BIP算法的。文献[4]提出了一种优化最小能耗广播树的r-shrink算法,该算法首先基于其他算法构造一棵广播树,然后以降低树的总能耗为目标,对树的结构进行调整。文献[5]提出了一种构造最小能耗广播树的模拟退火算法,利用BIP算法构造初始解,求解质量显著优于BIP算法,但仅对中小规模网络的最小能耗广播树问题求解效果较好。文献[6]提出了一个构造最小能耗多播树的蚁群算法,并在构造过程中使用r-shrink算法优化多播树的构造,优化效果较好,但运行时间较长。文献[7]提出了一种构造最小能耗多播树的PSOR算法,对到达非多播组成员的传输建立惩罚函数,在多播树的构造过程中基于收缩重叠传输范围改变多播树的结构,以减少多播能耗,并给出了理论上的最大近似比,该算法的时间复杂度较高。这些算法大多是直接针对最小能耗广播树的构造,很少是直接针对最小能耗多播树的构造,并且不同算法的适用情况不同。文献[8]提出了一种新型离散粒子群优化算法求解带权无向图的Steiner树问题,通过搜索最优中继节点来获取Steiner树,但由于无线传输本身所固有的多播特性使得无线网络的最小能耗多播树问题不同于Steiner树问题。文献[9]首先对最小能耗多播树问题进行整数线性规划,然后运用一种多相离散粒子群算法分布式地计算该整数线性规划的最优解,引入共生机制处理约束,该方法计算复杂度较高。
针对不同的中继节点选择对构造最小能耗多播树的影响,本文提出了一种改进的离散粒子群算法,引入惯性权重策略以平衡离散粒子群算法的全局搜索能力和局部搜索能力,以优化在使用全向天线和有向天线情况下的最小能耗多播树的构造,并通过相关的模拟实验验证了改进后的离散粒子群算法的优化能力,以及优化最小能耗多播树构造的有效性。
2 问题模型
考虑静态无线ad hoc网络由若干个无线节点构成,节点的位置已知。节点配有多个收发器可以同时支持多个多播会话,并且节点可以动态地调整自身的发送能量,本文只考虑节点的发送能量,不考虑接收能量和处理能量。
采用与文献[1~3]相似的天线模型和无线传播模型。在使用全向天线的情况下,假设均匀传播,信号能量按照 r-α衰减,r是到信号源的距离,α为通信媒介参数,其值取决于通信介质,通常介于2和4之间,本文假设α=2。当节点i的传输能量pi≥时,节点j可以成功接收到节点i发送的信号,rij为节点i和节点j之间的距离,βj为节点j的接收能量门限。假设所有节点的接收能量门限都相同且归一化为1。节点i的传输范围由节点i的传输距离ri所决定,节点i的传输能量pi=。在使用有向天线的情况下,假设节点的传输能量均匀分布在天线波束内,当节点 i的传输能量 pi≥θi/360×时,位于节点i的天线波束内的节点j可以成功接收到节点i发送的信号,θi为节点i的波束宽度。节点i的传输范围不仅取决于节点i的传输距离ri,还取决于节点 i的波束宽度 θi,节点 i的传输能量 pi=max{θi,θmin}/360×,其中 θmin为最小波束宽度。和使用全向天线相比,由于有向天线的波束较窄,使用有向天线使得在给定传输距离时可以节省传输能量,或者在给定传输能量时可以延长传输距离。位于节点 i传输范围内的节点都可以接收到节点 i所发送的信号,即无线传输本身具有多播特性(WMA, wireless multicast advantage),WMA特性使得无线多播不同于有线多播。
假设网络中各个节点的传输能量均确定,可以将网络模型化为一个有向图G=(V, E),V表示网络节点集合,边集E定义为:对于V中的任意节点i、j, <i, j>∈E当且仅当节点j位于节点i的传输范围之内。由于节点的传输能量p可以在一定的范围内进行调节(p≤pmax,pmax为节点的最大传输能量),在调节节点传输能量的同时,节点的传输距离发生变化,相关的网络链路被添加或移除,网络拓扑结构也相应发生变化。对于给定的网络G,以及多播会话指定的发送节点s、接收节点集D,D={d1,d2,…,dg},网络中除了发送节点s和目标节点D之外的其他节点都视为可参与多播会话的中继节点,本文研究的是如何建立基于源端的多播树 T(VT,ET),T的根节点是 s,T的任意叶子节点 l∈D,T中除了源节点s和目标节点D之外,其余节点为中继节点。
在使用全向天线的情况下,T中任一节点i的传输能量 pi取决于它的最大链路传输能量,即;在使用有向天线的情况下,T中任一节点i的传输能量pi取决于其最大链路传输能量和其波束宽度,即树 T的总能耗 p(T)为各个节点的能耗之和,即
假设网络中各节点的位置相对固定,每个节点的最大传输能量均为 pmax,pmax应足够大以使得多播会话得以进行。求解最小能耗多播树问题可表示为:对于给定的网络G,以及多播会话指定的源节点s和目标节点集D,寻找一棵以源节点s为根并且可以到达所有目标节点D的树T,在满足节点传输能量 p≤pmax的条件下为节点分配合适的传输能量,使得树的总能耗p(T)最小。
3 改进的离散粒子群算法
粒子群优化(PSO, particle swarm optimization)[10,11]算法是一种利用粒子群体进行随机搜索的智能优化算法。PSO由一群粒子组成,每个粒子代表问题的一个潜在解,具有一个随机速度,飞行于解空间执行随机搜索。搜索过程从问题的一个解集开始。PSO模拟社会行为,每个粒子记录自身所经历的最好位置,并且学习群体所经历的最好位置。粒子在飞行过程中追踪自身和群体迄今为止所经历的最好位置,并保持惯性,飞行速度具有随机性,以尽力搜索到全局最优解。PSO具有简单高效,并行性好、收敛快等优点。
假设在m维解空间中,执行搜索的粒子群由n个粒子组成,向量Xi=(xi1, xi2, …, xim)T表示第i个粒子的位置,向量Vi=(vi1, vi2, …, vim)T表示第i个粒子的速度。粒子在解空间执行搜索的过程中,向量Pi=(pi1, pi2, …, pim)T表示第i个粒子自身所经历的最好位置,Pi对应的适应度值为个体极值pbesti。每个粒子共享整个群体迄今为止所搜索到的最优解,全局极值索引 g为所有粒子中个体极值最优的那个粒子的索引,则向量Pg=(pg1, pg2, …, pgm)T表示所有粒子所经历的最好位置,Pg对应的适应度值 pbestg为全局极值。在连续粒子群算法中粒子的速度和位置按下式更新:

其中,c1、c2表示加速因子,通常取值为2;rand1()、rand2()为均匀分布在区间[0,1]上的随机函数;粒子速度被限制在某个范围之内,即|vij|≤vmax,vmax表示粒子运动速度的最大值。
在离散粒子群优化(DPSO,discrete particle swarm optimization)算法[12]中,粒子位置Xi的每一维 xij取值仅限于 0和 1,粒子速度 Vi的每一维vij表示xij取值为1的可能性,vmax通常取值为6.0。粒子速度仍按式(1)更新,粒子位置按下式更新:
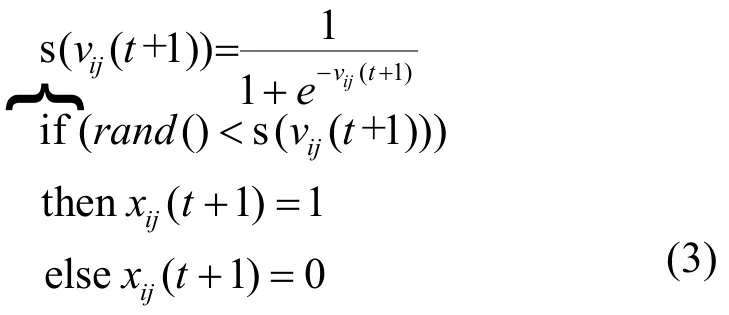
其中,s(vij(t+1))为sigmoid函数,rand()产生服从在区间[0,1]上均匀分布的随机数。
为了提高算法获取最优解的能力,通常在计算前期进行有效的全局搜索,以定位最优解的大致位置,在计算后期进行局部搜索,以获得精确度较高解[13~15],然而DPSO算法不能有效地平衡全局搜索能力和局部搜索能力。令Δv=vij(t+1)-vij(t)=c1rand1()(pij-xij)+c2rand2()(pgj-xij),当 pij=pgj=1,xij=0 时,Δv>0,vij增大,s(vij)增大,xij=1的概率增大;当pij=pgj=0,xij=1 时,Δv<0,vij减小,s(vij)减小,xij=0的概率增大;当xij=pij=pgj时,Δv=0,vij不变,s(vij)不变,xij以原有概率保持不变;当 pij≠pgj时,xij趋于pij或pgj。因此,在DPSO算法中,粒子追寻极值点的能力较强,算法的局部搜索能力较强,但算法容易早熟收敛,全局搜索能力较差。
在连续粒子群算法中,通常使用惯性权重w来平衡算法的全局搜索能力和局部搜索能力[13,14],w通常初值为 0.9,随着迭代的进行而线性下降至0.4[13~15]。然而这种逐渐递减的惯性权重不能直接适用于DPSO算法。如果DPSO算法使用惯性权重w,则 vij(t+1)=wvij(t)+c1rand1()(pij-xij)+c2rand2()(pgj-xij),Δv=vij(t+1)-vij(t)=(w-1)vij(t)+c1rand1()(pij-xij)+c2r and2()(pgj-xij),c1rand1()(pij-xij)+c2rand2()(pgj-xij)使粒子具有局部搜索能力,(w-1)vij(t)具有随机性和无记忆性,使粒子具有扩大搜索空间的趋势、探索新区域的能力,从而使粒子具有全局搜索能力。当0≤ w≤1时,随着w的减小,|(w-1) vij(t)|逐渐增大,全局搜索能力逐渐增强,反之,w越大,|(w-1) vij(t)|越小,局部搜索能力越强。因此,逐渐递减的惯性权重不适用于DPSO算法。
为了克服DPSO算法易于早熟收敛、全局搜索能力较差的问题,在DPSO算法中引入一种逐渐递增的惯性权重,以有效地平衡算法的全局搜索能力和局部搜索能力,提高算法获取全局最优解的能力。在计算前期,使惯性权重w由wa(wa[0,1])∈逐渐增大至wb(wb[0,1]∈,wb>wa),从而使算法具有较强的全局搜索能力;在计算后期,使惯性权重w保持为 wb不变,从而使算法具有较强的局部搜索能力,以进行精细的局部搜索。在改进后的DPSO算法(MDPSO,modified DPSO)中,粒子速度按式(4)更新,惯性权重按式(5)更新:

其中,td为增强全局搜索能力的时期,wa、wb、 td需根据具体情况进行设定。
4 构造最小能耗多播树的粒子群算法
MIP(D-MIP)算法[2,3]是基于 BIP(D-BIP)算法的,利用了无线传输的 WMA特性,首先由BIP(D-BIP)算法构造一棵广播树,然后修剪该广播树来获得多播树,其步骤如下。
Step1 初始化多播树T(VT,ET)只包含源节点s,VT←{s},ET←∅,初始化 V为网络中所有节点的集合。
Step2 对于任意一对节点 i和节点 j,i∈VT,j∈V-VT,计算将j作为i的孩子节点后节点i的能耗pi,j,如果 pi,j≤pmax,计算节点i所增加的能耗Δi,j←pi,j-pi,其中,pi为j成为i的孩子之前节点i的能耗。
Step3 如果对于任意一对节点 i和节点 j,i∈VT,j∈V-VT,pi,j>pmax,返回计算失败。
Step4 找到最小的Δi,j对应的节点i和节点j,将节点j加入VT,将边<i, j>加入ET。
Step5 如果 VT≠V,则转 Step2。
Step6 对T进行修剪,剪除对于到达目标节点所不需要的边,即如果节点及其下游节点中不包含目标节点,就将其排除。
Step7 输出多播树T及其总能耗,返回计算成功。
可见,MIP(D-MIP)算法在构造多播树时,将网络中除了源节点和目标节点之外的其他所有节点都作为中继节点参与多播树的构造,未考虑对参与多播树构造的中继节点进行筛选,导致算法结果误差较大。如果节点的最大传输能量pmax较小,会导致网络无法连通,算法将返回计算失败。
图1所示的一个实例演示了2种不同的中继节点选择对MIP算法计算结果的影响。在该实例中,网络共有5个节点,各节点的坐标分别为n1(15,11)、n2(10,12)、n3(15,5)、n4(2,6)、n5(2,9),其中,n2为源节点,n3、n4为目标节点,节点的最大传输能量无限制即pmax=∞。如果使用除了源节点和目标节点之外的其他所有节点(包括 n1、n5)作为中继节点参与多播树的构造,使用MIP算法构造多播树:初始时 VT={n2}、V={n1,n2,n3,n4,n5},首先选择距离源节点n2最近的节点n1加入多播树得到VT={n2,n1},然后根据最小化能耗增加原则,依次选择节点 n3、n5、n4加入多播树,结果如图 1(a)所示,节点 n2的能耗p2=max{,}=73,节点n5的能耗p5==9,节点 n1的能耗 p1==36,多播树的总能耗为p2+p5+p1=118。如果仅使用节点n5作为中继节点参与多播树的构造,使用MIP算法构造多播树:初始时 VT={n2}、V={n2,n3,n4,n5},首先选择距离源节点n2最近的节点,由于节点n1未参与多播树的构造,所以选择节点 n5加入多播树得到 VT={n2,n5},然后根据最小化能耗增加原则依次选择节点 n3、n4加入多播树,结果如图 1(b)所示,节点 n2的能耗p2=max{,}= 74,节点n5的能耗p5==9,多播树的总能耗为p2+p5=83。

图1 不同中继节点选择对MIP构造最小能耗多播树的影响
由此可见,选择不同的中继节点集对MIP算法的计算结果影响较大,可以通过比较MIP算法对不同中继节点集求得的结果,来获取一个最优中继节点集,从而降低 MIP算法的计算误差。假设集合 R={u1,u2,…,um}表示网络中除去源节点和目标节点之外其他所有节点的集合,则 R的幂集就表示该问题的解空间,由于MDPSO算法是对问题解空间的一次全局搜索过程,因而可以使用MDPSO算法求解最优中继节点集,从而优化最小能耗多播树的构造。在MDPSO算法中,每个粒子的位置代表一个中继节点集,粒子i位置Xi的第j维xij=1表示该维对应的中继节点uj(uj∈R)参与多播树的构造,xij=0表示uj不参与多播树的构造,粒子的维数为网络中除去源节点和目标节点之外其他所有节点的个数,即为|R|。在MDPSO算法中,在使用全向天线的情况下,使用MIP算法计算粒子的适应度值,在使用有向天线的情况下,使用D-MIP算法计算粒子的适应度值,即在选择了特定中继节点集的基础上,使用MIP或D-MIP算法构造多播树,并计算树的总能耗。对于选定的某个中继节点集,由于pmax的限制,由中继节点以及多播会话指定的源节点和目标节点构成的子网络不一定能连通,因而该中继节点集不一定是可行解。求解最小能耗多播树的MDPSO算法如下。
Step1 随机初始化粒子位置X1,X2,…,Xn,xij{0,1}∈;随机初始化粒子速度V1,V2,…,Vn,|vij|≤vmax;初始化粒子个体极值 pbest1←∞,pbest2←∞,…,pbestn←∞;初始化全局极值索引g←1;初始化总迭代次数 duration;初始化迭代次数变量t←0;初始化粒子标识变量i←1。
Step2 如果t=duration,则转Step12。
Step3 按式(5)更新惯性权重w。
Step4 如果 i>n,则转 Step11。
Step5 使用 MIP(D-MIP)算法计算第 i个粒子的适应度值f(Xi),如果计算失败,转Step8。
Step6 如果f(Xi)<pbesti,那么更新个体极值点Pi←Xi,更新个体极值 pbesti←f(Xi)。
Step7 如果pbesti<pbestg,那么更新全局极值索引g←i。
Step8 按式(4)更新粒子的速度Vi。
Step9 按式(3)更新粒子的位置Xi。
Step10 i←i+1,转 Step4。
Step11 t←t+1,i←1,转 Step2。
Step12 输出全局极值点 Pg,输出全局极值pbestg。
5 实验结果
为了验证MDPSO算法协调全局搜索能力和局部搜索能力的有效性,采用文献[16]提出的二进制编码的基因型多样性的测度方法来度量粒子群的多样性,粒子群多样性,其中,n为粒子数,m为粒子的维数,hij为粒子 i到粒子 j的海明距离。以MIP算法计算粒子的适应度,比较MDPSO算法与DPSO算法在运行过程中粒子群多样性的变化情况。随机生成一个包含 50个节点的网络,节点随机分布在1 000m×1 000m的平面区域内,目标节点数为总节点数的 1/3,随机产生源节点s和目标节点集D,节点最大传输能量pmax=∞,对该网络分别运行MDPSO算法与DPSO算法。在选取粒子群规模时,如果粒子数越多,算法的计算时间越长,如果粒子数越少,算法计算结果的精确度越低,因此应综合考虑算法的计算精确度和计算时间,通过多次实验测试得出取粒子群规模 n=30较合适。每个粒子的位置代表一个参与多播树构造的中继节点集,粒子的维数为除去源节点和目标节点之外其余节点的个数,即m=50-1-50/3=33,算法总迭代次数duration=100,wa=0.4,wb=1.0,td=0.5duration。每种算法运行20次,统计每种算法在这 20次运行过程中每次迭代后粒子群的平均多样性,算法的粒子群多样性变化情况如图2所示。在DPSO算法运行过程中,粒子群的多样性很快降低,算法很快收敛,全局搜索能力较差。在MDPSO算法运行过程中,在计算前期,粒子群的多样性较高,全局搜索能力较强,在计算后期,粒子群多样性降低,局部搜索能力较强。因此,MDPSO算法有效地平衡了全局搜索能力和局部搜索能力。

图2 MDPSO和DPSO粒子群多样性变化情况比较
为了验证MDPSO算法的优化能力,对几个不同规模的网络分别运行 MDPSO算法和 DPSO算法。在使用全向天线时使用MIP算法计算粒子的适应度,在使用有向天线时使用DMIP算法计算粒子的适应度。每种算法对同一个网络运行 20次,统计求得平均解。粒子群规模 n=30,算法总迭代次数duration=100,wa=0.4,wb=1.0,td=0.5duration。网络节点随机分布在 1 000m×1 000m的平面区域内,目标节点数为总节点数的 1/3,随机产生源节点s和目标节点集D,节点最大传输能量pmax=∞。实验结果如表1所示,MDPSO算法求得的平均解普遍优于DPSO算法,表明MDPSO算法的优化能力要优于DPSO算法。
为了验证构造最小能耗多播树的MDPSO算法的性能,在基于Java 6.0的MyEclipse 8.5平台上实现了MDPSO算法,并在处理器为Intel Q6600、内存为2GB、操作系统为Microsoft Windows XP的主机上运行实验程序。为了考虑MDPSO算法对不同节点最大传输能量 pmax的适应性,对多种不同的pmax分别进行了实验。对于每一种pmax,与文献[6]和文献[17]类似,分别对30个不同的网络,每个网络进行30次实验,统计所有计算结果的总平均值。每次实验中随机产生源节点s和目标节点集D,同一个网络的30次实验中,每10次实验分别采用目标节点数为总节点数的 1/3、1/2、2/3。每个网络包含 50个节点,随机分布在1 000m×1 000m的平面区域内。MDPSO算法的总迭代次数 duration取为 30,wa=0.6,wb=1.0,td=0.5duration,和目标节点数分别为总节点数的1/3、1/2、2/3相对应,粒子数分别取为30、25、20。

表1 MDPSO和DPSO优化能力比较

表2 MDPSO和MIP计算结果比较
表2显示了在使用全向天线的情况下,对于多种pmax,MIP算法和MDPSO算法的运行结果。表3显示了在使用有向天线的情况下并且最小波束宽度 θmin=90°时,对于多种 pmax,D-MIP算法和MDPSO算法的运行结果。实验结果表明,对于不同的 pmax,MDPSO算法均能有效地优化最小能耗多播树的构造。在使用全向天线的情况下,当pmax较小时MDPSO算法在计算过程中所遇到的不可行解较多,随着pmax的增加不可行解逐渐减少;而在使用有向天线的情况下,由于有向天线减小了波束宽度,延长了通信距离,即使当pmax较小时不可行解也很少。与MIP(D-MIP)算法相比,MDPSO算法由于在计算过程中进行了多次迭代,其计算时间相对较长,然而,MDPSO算法本质上是利用粒子群体进行并行寻优,从而易于设计分布式并行程序来降低算法的执行时间。

表3 MDPSO和D-MIP计算结果比较
6 结束语
在无线ad hoc网络中如何构造最小能耗多播路由树是一个重要问题。本文首先分别分析了在使用全向天线和有向天线的情况下该问题的不同数学模型,针对不同的中继节点选择对构造最小能耗多播树的影响,提出了一种改进的离散粒子群算法,以优化最小能耗多播树的构造,最后通过模拟实验验证了改进的离散粒子群算法有效地优化了最小能耗多播树的构造。进一步的研究工作包括将MDPSO算法与一些局部优化算法相结合,以及如何更好地设定MDPSO算法的控制参数,以获取更优的近似最小能耗多播树。
[1] GUO S, YANG O. Energy-aware multicasting in wireless ad hoc networks: a survey and discussion[J]. Computer Communications,2007, 30(9):2129-2148.
[2] WIESELTHIER J E, NGUYEN G D, EPHREMIDES A. On the construction of energy-efficient broadcast and multicast trees in wireless networks[A]. Proceedings of IEEE INFOCOM’2000[C]. Tel Aviv, Israel, 2000. 585-594.
[3] WIESELTHIER J E, NGUYEN G D, EPHREMIDES A. Energy-aware wireless networking with directional antennas: the case of session-based broadcasting and multicasting[J]. IEEE Transactions on Mobile Computing, 2002, 1(3): 176-191.
[4] DAS A K,MARKS R J,EL-SHARKAWI M, et al. R-shrink: a heuristic for improving minimum power broadcast trees in wireless networks[A]. Proceedings of IEEE GLOBECOM’03[C]. San Francisco, CA, USA, 2003. 523-527.
[5] MONTEMANNI R, GAMBARDELLA L M, DAS A K. The minimum power broadcast problem in wireless networks: a simulated annealing approach[A]. Proceedings of the 2005 IEEE Wireless Communications and Networking Conference [C]. New Orleans, LA, USA, 2005. 2057-2062.
[6] HERNANDEZ H, BLUM C. Energy-efficient multicasting in wireless ad-hoc networks: an ant colony optimization approach[A]. Proceedings of the 2008 IEEE International Symposium on Wireless Communication Systems[C]. Reykjavik, Iceland, 2008. 667-671.
[7] MIN M, O'BRIEN A F, SHIN S Y. Partitioning-based SOR for minimum energy multicast tree problem in wireless ad hoc networks[A].Proceedings of the 18th International Conference on Computer Communications and Networks[C]. San Francisco, CA, USA, 2009. 1-6.
[8] ZHONG W L, HUANG J, ZHANG J. A novel particle swarm optimization for the Steiner tree problem in graphs[A]. Proceedings of the 2008 IEEE Congress on Evolutionary Computation[C]. Hong Kong,China, 2008. 2460-2467.
[9] YUAN P, JI C L, ZHANG Y, et al. Optimal multicast routing in wireless ad hoc sensor networks[A]. Proceedings of 2004 IEEE International Conference on Networking, Sensing and Control[C]. 2004.367-371.
[10] KENNEDY J, EBERHART R. Particle swarm optimization[A].Proceedings of the 1995 IEEE International Conference on Neural Networks[C]. Perth, Australia, 1995. 1942-1948.
[11] EBERHART R, KENNEDY J. A new optimizer using particle swarm theory[A]. Proceedings of the Sixth International Symposium on Micro Machine and Human Science[C]. Nagoya, Japan, 1995. 39-43.
[12] KENNEDY J, EBERHART R. A discrete binary version of the particle swarm algorithm[A]. Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics[C]. Orlando, FL, USA,1997. 4104-4108.
[13] SHI Y, EBERHART R. A modified particle swarm optimizer[A].Proceedings of the 1998 IEEE International Conference on Evolutionary Computation[C]. 1998. 69-73.
[14] SHI Y, EBERHART R. Empirical study of particle swarm optimization[A]. Proceedings of the 1999 Congress on Evolutionary Computation[C]. Washington, DC, USA, 1999. 1945-1950.
[15] SHI Y, E-BERHART R. Parameter selection in particle swarm optimization[A]. Proceeding of the 1998 Annual Conference on Evolutionary Programming[C]. San Dingo, CA, USA, 1998.591-600.
[16] 武晓今,朱仲英. 遗传算法多样性测度问题研究[J]. 信息与控制,2005, 34(4): 416-422.WU X J, ZHU Z Y. Research on diversity measure of genetic algorithms[J]. Information and Control, 2005, 34(4): 416-422.
[17] AL-SHIHABI S, MERZ P, WOLF S. Nested partitioning for the minimum energy broadcast problem[A]. LIUN 2007 II, Learning and Intelligent Optimization[C]. 2007. 1-11.
