体操团体赛队员选派问题研究

张炜 袁驵 叶燕清 贾祥 戴琪玮

（国防科学技术大学信息系统与管理学院 湖南长沙 410072）

中国体育健儿在各类赛事中积极拼搏，为国争光。作为运动队的管理者，在日常训练中可以统计各位运动员的训练成绩，得到运动员的成绩分布律。在参加特定比赛时，如何组建具体的最优参赛阵容，尤为重要。对这一问题，王磊建立规划模型，并通过仿真来估计夺冠概率；唐建国将这个问题转化为动态规划来求解；刘萍等建立两级目标函数，加权转化为单目标规划模型进行分析；杜欣等首先确定最优目标，然后寻找几种评定条件，进行优先排序，再根据排序后的约束条件进行筛选，最终得出最佳阵容；张雨等利用整数规划求解问题，并且利用随机模拟取值的办法，估计夺冠的把握。在问题的建模和求解分析上，这些研究都很成熟，但是都缺乏对所选方法合理性的分析。本文将充分讨论这个问题的各种解法，确定合适的策略和模型。

1 问题描述

现假设某届世界体操锦标赛团体决赛有个项目（例高低杠项目）组成，共有支队伍参赛。每个队至多有名运动员可以报名，每一个项目可以有名选手参加，取这名运动员的成绩作为该队在该项目上的有效得分。每个代表队的总分是所有参赛选手所得有效分之和，总分最高的代表队为优胜者[6]。某支代表队的各个队员在各个项目上的得分分布律已知，那么该如何组合最优阵容。

假设运动员出场顺序不影响团队的比赛成绩。每个运动员可以参加任意一项比赛项目，并且参加项目数量不受限制。比赛时所有运动员都可以正常参赛，不受疾病、心理等因素影响。

对决策问题，可以依据期望策略，最乐观策略，最悲观策略等准则。本文认为，利用最悲观策略组建阵容去参加比赛和冲击冠军，过于保守，是不合适的。因而选取期望准则和最乐观准则两种策略。

这个问题的目标应是阵容参赛的得分最高。假设所有运动员参赛项目不受限制，当参赛队伍在各个项目上获得的有效分最高时，该阵容总分最高，那么确定最优阵容就转化成在特定策略下，确定各个项目得分最高的组合，进而得到最优阵容。

设参加某个项目的阵容中有参赛队员 i(i=1,…,n)，该队员的分布律记为，则该参赛队员的期望得分，最乐观策略下得分表示 k个实数 lu相加、相乘。

2 模型

对这个问题的分析，有两种方法。本文将对同一个问题，分别运用这两种方法解决。事实上，这两种方法是等效的，最后将给出证明。

2.1 总体分布律法

最直接也最严密的思路是根据 m选 n的原则，排列组合出参赛队伍在各个比赛项目上的阵容（在一个项目上共有种组合），根据各个选手的得分分布律，可计算出该套阵容在该项目上的有效分分布律。根据分布律，利用两套准则，只需在各个项目上分别比较套阵容的 E和 M，选择最大值，对应在该项目上的理想组合，综合即得最优阵容。模型如下：

选择队员 i1,…,in组成一套阵容参加某个项目的比赛，则这套阵容的总体有效分分布律为

在期望策略下有：

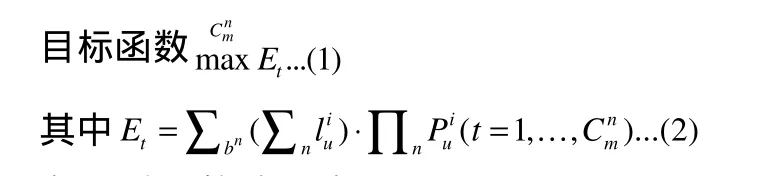
在最乐观策略下有：

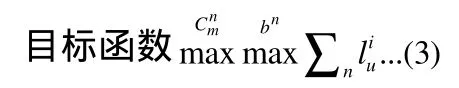
具体操作步骤如下：

步骤1：从全部运动员中不重复地选择n个运动员。

步骤2：针对某个项目，依次从n个运动员得分分布律中选择一个得分和对应概率，计算总体分布律的其中一项

步骤3：计算各个总体分布律的有效分期望值和最大值。

步骤4：所有分布律中有效分期望或最大值最大的阵容，即为该队在该项目上的最佳阵容。

2.2 个人分布律解法

按总体分布律解法计算，是通过对阵容总体分布律进行相关计算得到结果。虽然思路清晰直接，但是计算量过于庞大。若换种角度来处理，可首先根据个人得分分布律，计算各运动员在各个项目中的期望得分、最高得分，再根据这些得分，去确定各个策略下，有效分最高的阵容。参赛队员i的期望有效分记为 Ei，最高有效分记为 Mi。

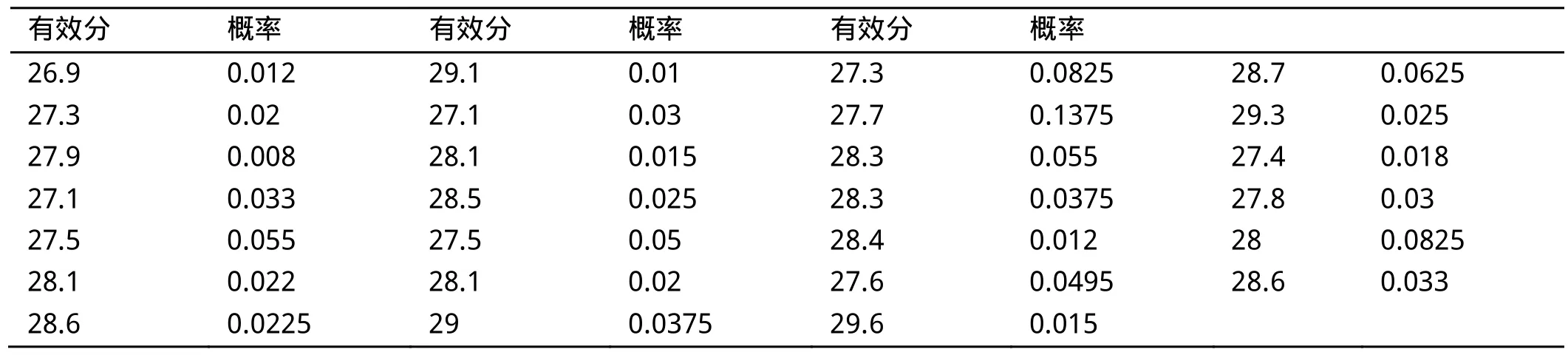
表1 运动员1、2、3组成的阵容参加自由体操的有效分总体分布律

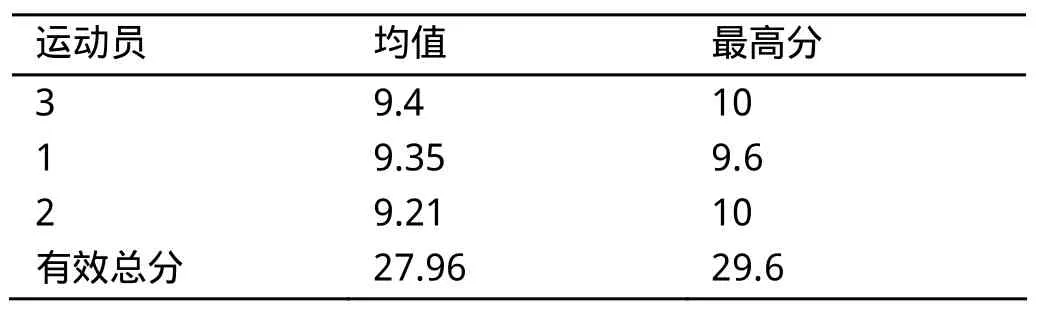
表2 运动员1、2、3的个人分布律及该阵容的期望分和最高分

操作步骤如下：

步骤1：针对某个项目，依次利用个人分布律，计算各名运动员的有效分期望值和最大值。

步骤2：从全部运动员中不重复地选择n个运动员。

步骤3：计算各个组合阵容下的期望总分值和最大总分值。

步骤4：所有组合中有效分期望或最大值最大的阵容，即为该队在该参赛项目上的最佳阵容。

3 结果与讨论

某项体操比赛中，每个项目允许有3名运动员上场比赛，选取其中这3名运动员的成绩作为该队在这个项目的参赛成绩。以运动员1、2、3组成的阵容参加自由体操为例，编写程序计算得到总的分布律（表1）。得到27.96、29.6分。仍以运动员2、3、4组成的阵容参加自由体操为例，运用个人分布律法计算，得到相关数据见表2。

4 等效性的证明

两种方法的计算结果相同。事实上两种方法是等效的，显然后者将更简便。证明如下：

记在特定参赛项目上，某阵容的总体分布律期望为 E、最高分为 M。

先证明在最乐观策略下：

再证明在均值策略下：

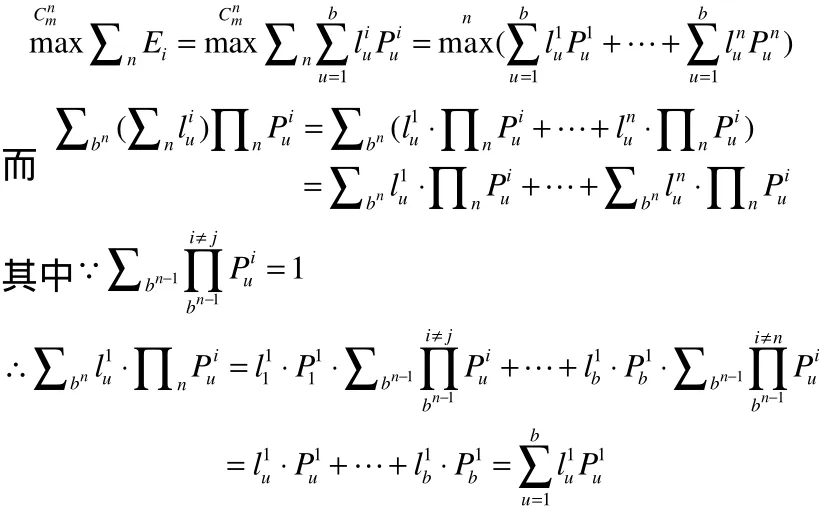
同理

则得结论

证明完毕。

既然两种方法是等效的，而由后者计算可以大大简化计算量，尤其是运动员分布律比较复杂时，更有必要利用后者来求解问题。且由证明过程可以发现，对于阵容的选取，选取每个运动员的策略可以任意组合。例如，选取某套阵容时，运动员依据均值策略，根据最乐观策略。

5 结语

本文对已有平时训练成绩的运动员组合参赛问题进行了探析。鉴于该问题，已有很多学者进行研究，模型的建立和方法都很成熟，所以本文并没有重点讨论如何建立模型和如何求解，而是解决了众多文章中没有讨论所选方法合理性的问题，通过多个角度的方法解析和等效性证明，既明确了简便算法，也可以证明众多参考文献中模型求解算法的正确性。