模式搜索开窗拟合系统误差的滤波方法研究

2012-08-07刘庆元邹程昊

江汉大学学报（自然科学版） 2012年3期

关键词：系统误差开窗残差

刘庆元，邹程昊

（中南大学地球科学与信息物理学院，湖南长沙 410083）

模式搜索开窗拟合系统误差的滤波方法研究

刘庆元，邹程昊

（中南大学地球科学与信息物理学院，湖南长沙 410083）

为消除导航数据中的系统误差，提高定位精度，在开窗拟合系统误差的卡尔曼滤波基础上，研讨窗口长度的确定方法和过程。引入最优化思想，通过模式搜索的方法完善了窗口长度确定环节，使之更适于编程。模式搜索开窗拟合系统误差的滤波方法在过滤系统误差时有更广的适用性。

滤波；拟合；编程；搜索；系统误差

0 引言

随着现代科学技术的发展，对于定位精度的要求越来越高，定位和导航技术进入了一个崭新的时代。定位包含许多误差源，对其进行处理的重要方法之一是动态滤波法，经典的最优滤波包括维纳（Wiener）滤波和卡尔曼（Kalman）滤波。Wiener滤波采用频域法，其作用受到限制；Kalman滤波采用的是时域状态空间法，有适合多变量系统和时变系统、适合非平稳随机过程、算法原理是递推从而适合计算机编程实现这三大优点。因此，动态导航数据的实时处理或事后处理经常采用动态Kalman滤波方法[1］，将真正的信号和状态从含有随机干扰的观测信息中最优地实时估计出来。估计过程一般假设系统的动态噪声和观测噪声统计特性为已知的白噪声序列，该序列均值为零。

系统误差的特性非常复杂，既有延续性，又有偶然性[2］，所以当实时动态导航定位过程中含有系统误差时，偏离白噪声理想假设的观测向量或偏离理想假设的动力学模型可能会给动态滤波结果带来偏差甚至发散。国内一些学者用参数、非参数或半参数来估计系统误差[3-4］，本文则是对观测误差和模型误差做近似假设，即在较短的观测时间段内，如从时刻tk-n至时刻tk，观测系统差和动力模型系统差仅发生微小变化，则可以采用某些简单方法进行拟合[5］。对此杨元喜提出一种对观测系统差和动力学模型差直接拟合并对相应协方差矩阵做出近似估计的方法[6-7］。笔者试图深入探讨这一方法的实现细节，将模式搜索法[8］应用于窗口长度确定过程，最后使用仿真算例与原方法进行对比。

1 基于系统误差及其协方差矩阵拟合Kalman滤波模型

Kalman滤波的基本思想是用包含正交状态变量的微分方程模型来描述时变线性系统，将过去的测量估计误差合并到新的测量误差中来估计将来的误差。Kalman滤波是满足理想前提条件的最优状态估计法，从随机模型可以看出，只有在动力模型噪声向量和观测误差向量期望值都为零的前提条件下，它才能起到预期效果。而当系统误差出现时，滤波前提无法满足，于是滤波效果差甚至出现发散现象。滤波结果可见于本文的算例比较与分析。下面简单介绍在Kalman滤波中系统误差及其协方差的拟合原理和方法。

令Wk为动力模型噪声向量，ek为观测误差向量，分别为Wk和ek的协方差矩阵。若在固定的观测历元间视系统误差为常量或围绕某常量随机变化，则可以采用固定窗口内的观测残差和状态预测残差向量的均值进行拟合解算[9］。uk为观测误差向量存在的系统误差，sk为动力模型噪声向量存在的系统误差，因此观测模型和动力模型误差的期望不为零，即

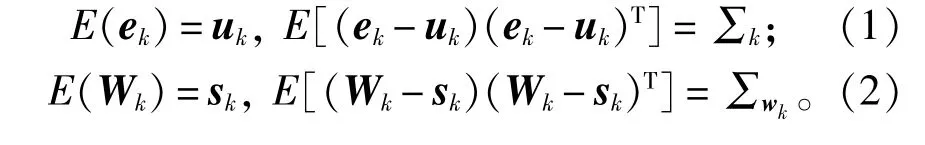
通过分析观测向量系统误差

其中Lk为观测向量，Ak为设计矩阵，Xk为载体的状态方程，Vk为Lk的残差向量。

当Lk存在系统误差时，导致系统状态估值有偏。而通过动力模型导致有偏。

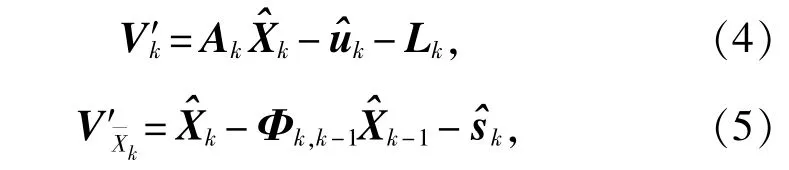
其中Φk，k-1为状态转移矩阵。与观测残差、预测残差以及状态残差所不同的是，V′k为Lk在含有系统误差前提下的残差向量，在含有系统误差前提下的残差向量。

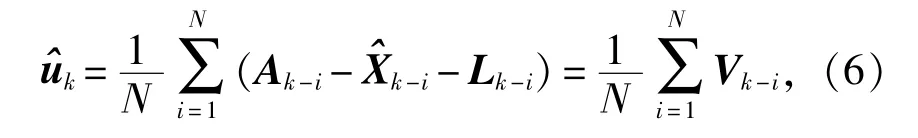
即通过前面的观测数据求出观测系统误差，由此得到观测向量消除了系统误差后的协方差矩阵拟合值

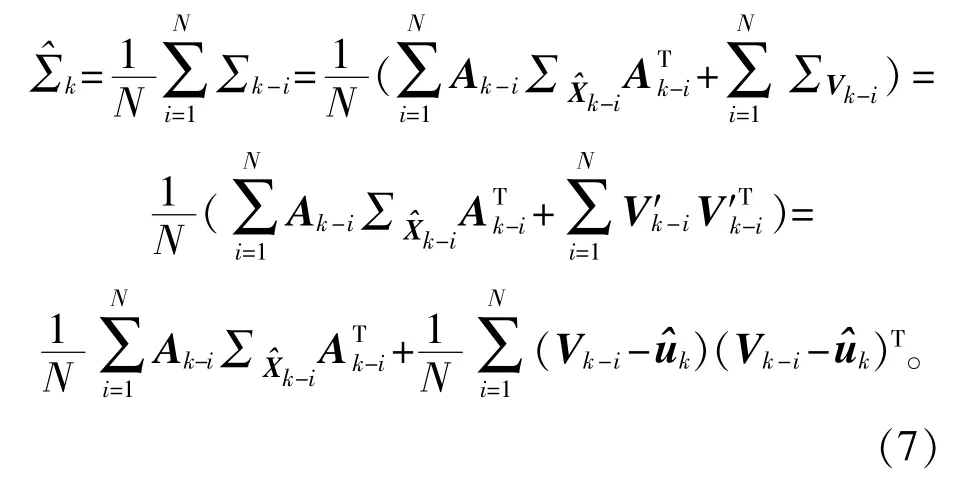
同样通过拟合求得动力模型系统差：

由此得到消除系统误差后的状态预报向量协方差矩阵拟合值

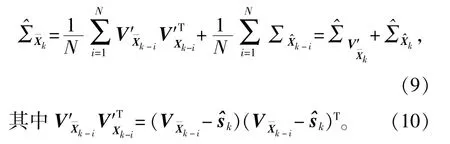
这种估计的直接好处是在卡尔曼滤波过程中，不仅抵制了观测系统偏差和动力模型系统偏差的影响，而且可以求出这些系统偏差的数值，即从函数模型和随机模型两方面同时改进导航滤波的可靠性。具体实施模型为，预测部分：

其中I为与KkAk同阶的单位矩阵。

因为指定窗口长度是一个可以人工调控的数值，不同大小的窗口长度会导致不一样的滤波结果。其目标函数可以表示为

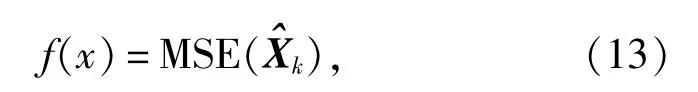
它是以窗口长度x为自变量，以滤波效果衡量指标均方误差MSE为因变量的函数。因窗口长度值必为整数的性质，这是一个离散不可导函数。指定合适的窗口长度以获得最佳的滤波效果是一个最优化问题。

2 模式搜索法在窗口长度搜索中的应用

解决最优化问题已有很多方法，例如遗传算法、神经网络、模拟退火等，这些方法在应用过程中各有优劣[10］。模式搜索法是一种解决最优化问题的直接方法，在计算时不需要目标函数的导数，所以在解决不可导的函数或者求导异常麻烦的函数的优化问题时非常有效。

模式搜索法也称步长加速法，用于求n元函数f（x1，x2，…，xn）的极大值或极小值，这个方法由两类“移动”组成：一类是“探索性”的移动，也叫轴向移动，用于探测函数的下降方向，在这一步骤，从起点分别沿各个方向按照初始步长a0进行探测，选出探测出的最优结果为这一步的终止点当探测不到更优结果时缩短步长，直到达到最小步长ε，这一步骤主要功能是揭示目标函数变化规律。另一类是“模式性”的移动，可以看成是一种加速，这种运动利用发现的函数变化规律，从而可以沿着有利的方向寻找更好的点，其探测的方向是上一步轴向移动的方向探测的步长则在这一方向上乘上加速因子λj，模式移动完成后，旋即在点上进行一次轴向搜索得到点然后分以下两种情况处理：

（II）若未能搜索到更优点，则回到上一轮轴向搜索的最终点：令将步长a缩小，重新进行探测性移动，如果步长a满足那么迭代结束。

模式搜索法可能要计算很多点的函数值才能得到目标函数的近似极小点。但是它易于在计算机上实现，实际效果也不错，因此被认为是一种很可靠的方法。

图1 添加搜索功能后流程

3 算例比较与分析

开窗拟合系统误差的Kalman滤波已被证实能有效去除观测信息中的系统误差，即使是在观测信息不含系统误差情况下，其仍能部分改善经典Kalman滤波[6］。

本文使用Matlab模拟数据说明模式搜索开窗拟合系统误差方法的先进性。模拟一个陀螺仪在旋转载体中的匀速转动。设载体观测方程为

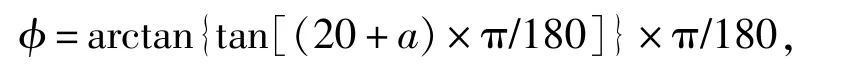
其中φ是角速度偏移量，观测速度扰动满足a～N（0，10），观测系统对角速度偏移进行采样，采样间隔为1 s，状态噪声满足w～N（0，1）。所以初始观测值方差与初始动力模型噪声矩阵分别为10和1。为计算简易起见，设状态转移矩阵Φk，k-1=1，观测变化矩阵Ak=1。

构造两个略有差异的观测模型系统误差，分别添加到载体观测方程。

本算例利用Matlab模拟200个历元观测值，在滤波过程中，设窗口长度为wN。然后对上述数据采用4种对比计算方案。

方案1：加入系统误差1的模式搜索开窗拟合系统误差Kalman滤波（见图2）。

图2 加入系统误差1的模式搜索开窗拟合系统误差Kalman滤波

方案2：加入系统误差2的模式搜索开窗拟合系统误差Kalman滤波（见图3）。

图3 加入系统误差2的模式搜索开窗拟合系统误差Kalman滤波

方案3：加入系统误差1的固定窗口长度（窗长为10）拟合系统误差Kalman滤波（见图4）。

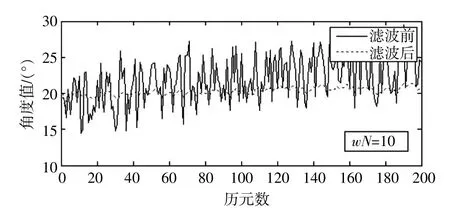
图4 加入系统误差1的固定窗口长度（窗长为10)拟合系统误差Kalman滤波

方案4：加入系统误差2的固定窗口长度（窗长为10）拟合系统误差Kalman滤波（见图5）。

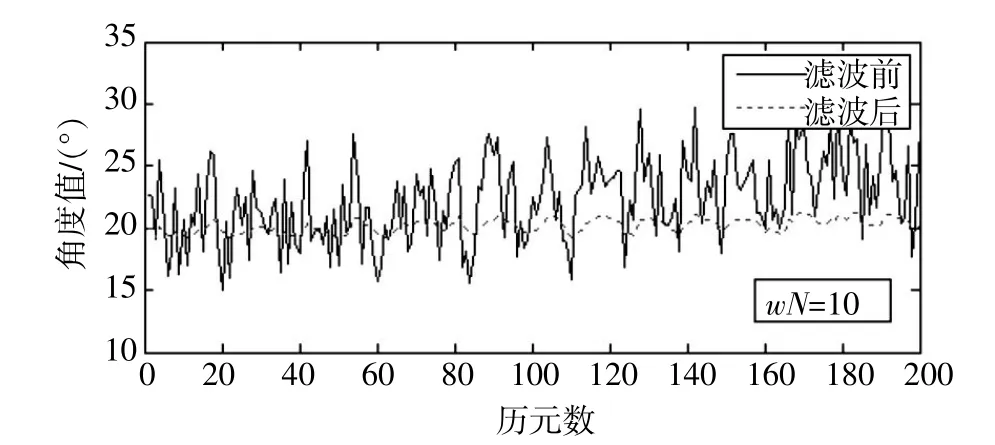
图5 加入系统误差2的固定窗口长度（窗长为10)拟合系统误差Kalman滤波

4种方案输出量统计与滤波前统计对比由直方图分别表示为图6～图9。

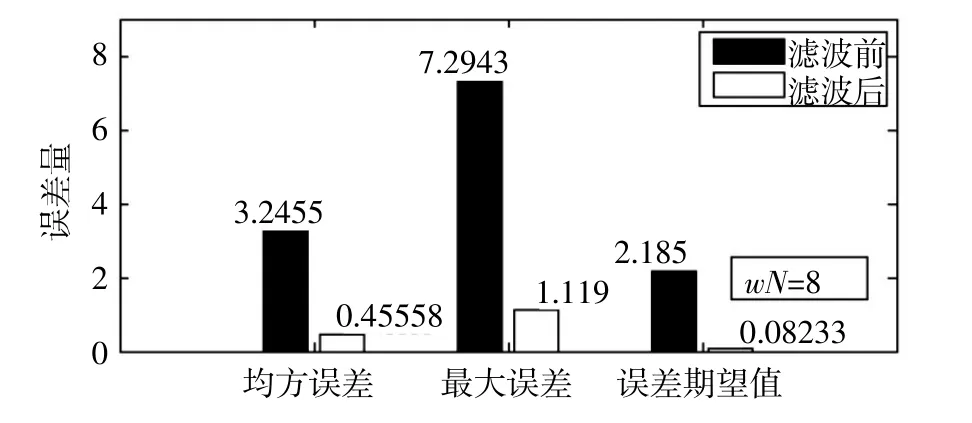
图6 方案1统计数据

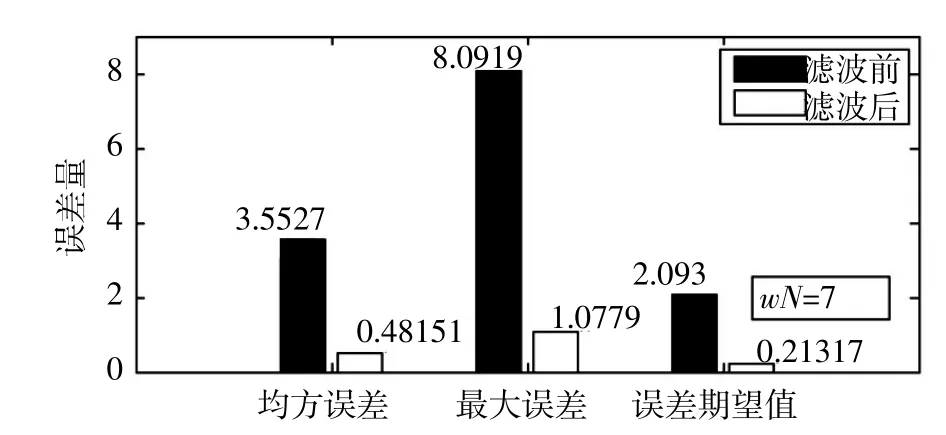
图7 方案2统计数据

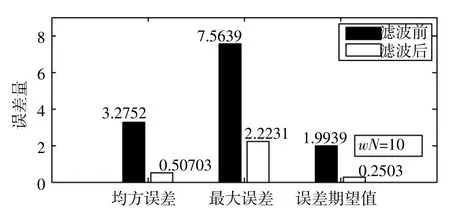
图8 方案3统计数据

图9 方案4统计数据

通过对算例图示的分析可以得出如下结论：

1）模式搜索开窗拟合系统误差的滤波方法能够适用于不同大小的系统误差，分别搜索出最优的窗口长度。对于系统误差1，得到的最优窗长为8（见图2和图6）；对于系统误差2，得到的最优窗长为7（见图3和图7）。

2）模式搜索开窗拟合系统误差的滤波方法相比取固定窗长的方法而言，滤波后的均方误差更小，由图6对比图8：0.455 58＜0.507 03；图7对比图9：0.481 51＜0.549 29。

4 结语

当观测模型和动力学模型含有系统误差时，经典Kalman滤波结果将受到歪曲，因为经典Kalman滤波器是满足理想条件下的一种最优状态估计算法。观测信息中存在系统误差时，相应的观测残差均值和状态预报残差均值不为零，利用开窗法拟合得到的系统误差对模型进行修正，则可在很大程度上减弱系统误差的影响，而以往方法没有解决滤波时如何选取窗口长度参数的问题。模式搜索法的引入，使得这一滤波方法更便于编程实现。它能较快地获取窗口长度参数，对不同的系统误差，能获取与之适应的窗口长度，从而使得原算法有了更广的适用性。

[1］胡国荣，欧吉坤.改进的高动态GPS定位自适应卡尔曼滤波方法[J］.测绘学报，1999，28（4）：290-294.

[2］周江文.系统误差的数学处理[J］.测绘工程，1999，8（2）：1-4.

[3］陈永奇，Chrzanowski A.模拟GPS精密测量系统误差的若干问题[J］.武汉测绘科技大学学报，1994，19（4）：310-314.

[4］施闯，刘经南，姚宜斌.高精度GPS网数据处理中的系统误差分析[J］.武汉大学学报：信息科学版，2002，27（2）：148-152.

[5］张金槐，蔡洪.飞行器试验统计学[M］.长沙：国防科技大学出版社，1995.

[6］杨元喜，张双成.导航解算中的系统误差及其协方差矩阵拟合[J］.测绘学报，2004，33（3）：189-194.

[7］Yang Y，Xu T H.An adaptive Kalman filter based on sage windowing weights and variance components[J］. The Journal of Navigation，2003，56（2）：231-240.

[8］席少霖，赵凤治.最优化计算方法[M］.上海：科学技术出版社，1983.

[9］张勤.非线性最小二乘理论及其在NQR定位中应用研究[D］.武汉：武汉大学，2002.

[10］吴兴远.模式搜索法在最优化问题中的应用[J］.软件导刊，2009，8（8）：122-123.

LIU Qing-yuan，ZOU Cheng-hao
（School of Geosciences and Info-Physics，Central South University，Changsha 410083，Hunan，China）

The paper discusses the way of improving positioning accuracy by eliminating the systematic errors in the navigation data.Based on the Kalman filter of window fitting systematic errors，the method and process for determining the window length are discussed.The optimized idea was introduced，which was made to be more suitable for coding by the pattern-search methods for determining window length.The Pattern-search moving windows method has wider applicability in fitting systematical errors.

filtering；fitting；coding；searching；systematic error