一种基于“莱因达”准则的区域自动站实时资料应用方法
2012-08-07陈正旭王俊骄洪月英
陈正旭,王俊骄,洪月英
(1.浙江省气象信息网络中心,浙江 杭州 310017; 2.杭州市气象局,浙江 杭州 310008)
一种基于“莱因达”准则的区域自动站实时资料应用方法
陈正旭1,王俊骄2,洪月英1
(1.浙江省气象信息网络中心,浙江 杭州 310017; 2.杭州市气象局,浙江 杭州 310008)
针对区域自动站降水实时资料应用中出现的问题,提出一种利用改进的 “莱因达”准则处理区域自动站实时降水数据的方法。首先由欧式距离聚类得到样本空间,再计算样本的均值和残差,然后给出了可疑度的定义,从而计算出各个站点的可疑度。最后通过实际数据进行参数分析,证明了算法的有效性、实用性。
区域自动站;质量控制;实时资料;莱因达准则
0 引言
区域自动站观测资料是中尺度、短时效天气预报不可缺少的重要资料源之一。由于仪器、维护、环境等多种原因,其探测资料的可靠性不如常规站。而往往在梅讯期期间、台汛期期间或某个降雨过程,需要利用区域自动站提供的数据资料制作决策服务材料。如在绘制等值线色块图时,往往会受“异常”数据的影响,导致生成的等值线色块图不美观、缺乏合理的逻辑性,或不能总体上把握研究对象的空间变化特征。
当然,处理类似问题最好的方法就是实时数据质量控制,将存在 “异常”的站点数据快速剔除,但国内对自动气象站数据质量控制主要是着眼于历史数据,而对实时数据质量控制的应用较少。传统的方法是通过人工审查、经验分析等方法剔除可疑数据。但随着计算机自动化的普及、信息量的增大,且需将各种AWS观测资料及时进行气象服务和业务使用,数据质量控制必须由计算机来完成。国外有许多学者对气象资料质量控制方法做过研究[1-2],王新华等[3]、任芝花等[4]对非实时资料做过质量控制,王海军等[5]提出自动气象站实时资料自动质量控制方法。但实时信息的检验和历史质量控制有一些不同,如对于历史质量控制可知道该时刻前后的时刻和空间的数据,而实时数据实效性强,只知道当前时刻空间的站点数据。如果分析某个时间段的数据,则就仅仅知道空间的数据。因此传统的质量控制方法不能满足服务的高时效性。
为了快速分析、处理和应用区域自动站观测的资料,并及时进行气象服务和业务使用,笔者提出一种结合改进“莱因达”准极值控制方法。通过该方法对所有站点数据进行综合分析,计算它们的可疑度,并对有“疑问”的数据进行标注。在数据应用中,使用人员可结合可疑度和实际需求对“疑问”数据进行合理的舍弃,使生成的等值线色块图可信、可用、美观。
1 基本原理
考虑到如果分析某个时间段的数据,区域自动站提供的资料则仅仅是分布在不同地理位置的空间站点数据,并不存在历史可比性。同时种种原因又会使少数区域自动站的数据出现 “异常”,降水资料特别明显,在实际业务中,通过软件监控、人工判断(结合雷达估测等),往往已经对一些不合理的异常大值进行了处理,但对异常小值未进行处理。因此,如果直接利用区域自动站的数据绘制等值线图时[6],会发生“在降水量大值区出现梯度递减区域”、“较多逗点状小值”等不符合逻辑的问题。同时,考虑到任何质量控制的方法都不能保证找出所有的“异常点”,也不能保证不误判。因此本文仅仅是根据算法计算各个数据的可疑度,至于是否采用均由数据应用人员决定。由于降水资料具有标量单位的气象要素,故可利用极值控制方法对区域自动站提供的原始数据进行分析[2],计算出站点数据的可疑度。
由于传统的“莱因达”准则可用于判别样本集合中的某个样本是否为异常点,本文仅给出可疑度,由数据使用人员判别是否异常。为此,根据整个区域的站点分布,针对第i个站点找到距该站点最近的“欧式距离”的N个其他站点,作为该站点的站点集合Ωi。在一定的假设基础上,利用改进的“莱因达”法则计算站点的可疑度Wi,从而完成数据质量的预处理控制。
2 极值控制法
根据气象要素的特点,用各种方法确定出适当的极值作为判断数据正确与否的上下限。当实时观测数据超出极限,则认为该数据是可疑的,将其剔除。利用极值法进行数据质量检查的关键是如何确定极值的大小,极值的大小关系到是否能够达到预期的目的。上下限过大,达不到控制目的;过小,会造成 “弃真”,把真实的数据当作错误的处理。极值的选取方法多种多样,一般通过凭经验或者历史资料给某个要素确定极值上下限,不具有通用性,特别是当只有空间数据时。
因此,本文通过最短距离聚类得到某个站点的样本集合,再利用“莱因达”准则计算数据合理范围[7],从而得到该站点的可疑度。
2.1 最短距离聚类和标准“莱因达”准则
在整个区域的站点分布下,在聚类水平N下,假设某些站点的“欧式距离”相对较短,则认为这些站点的数据服从同一个正态分布,那么就可认为这些站点的数据为一个站连续观测若干次的数据,可利用“莱因达”法则进行判别。
因此,针对第i个站点,根据其他站点与该站点之间的距离,将距离最短的N个站点作为该站点的站点集合Ωi(不包含第i个站点本身)。其中,在Ωi中的数据服从正态分布。
根据误差理论,一般情况下,在某个小区域内站点的随机误差vi服从正态分布,σ为标准差,一般是未知的,通常用贝塞尔公式算得S代替,以集合均值Ri代替真值,对某个观测数据Ri,若为异常点,其残差vi满足

其中k为阀值系数,一般取3(或2),至于3S或2S与显著性水平α有关,3S相当于α=0.01, 2S相当于α=0.05。表示Ωi内的站点个数。
2.2 改进的“莱因达”准则
残差vi是否满足(1)式与参数有关。但由于在站点集合Ωi中,两两站点之间存在不同的距离,因此对于集合的均值不能简单取算术平均值。在运用中,业务人员对异常大值和异常小值的容忍度往往不一样,因此阀值系数k可设定不同的阀值系数k1、k2。为了消除量纲,使S能适用于同一组阀值系数,对于集合Ωi中的数据必须先标准化后才可分析。
将公式(1)改写如下:

定义1 对于第i个观测点,在集合Ωi中其观测数据Ri的可疑度Wi定义为

从定义1可知,任何数据Ri的可疑度Wi均为0或正数。若Ri满足(2)式,则可疑度不为零,反之则为0。
2.3 算法的基本流程图
综合以上分析,得到本研究的算法基本流程图(见图1)。

图1 算法的基本流程图
3 实证应用
以浙江省2011年6月5日20点至2011年6月21日20点的1 627个区域自动站观测的累计降水资料为数据源,利用算法计算可疑度大于零的站点。
为了能分析算法的效能,针对该数据源进行人工审核和确认,从而确定有问题的站点信息,总共有18个站点在该过程中存在问题(用于计算误判和漏判的站点数),全部集中在异常偏小值。主要原因在于:站点设备故障数据不能正确采集或者未连续上传小时文件,从而导致累计值偏小很多。
根据本文的算法,自动站降水资料使用效果直接取决于各种参数:阀值系数k1、k2;聚类水平N。在以下的参数分析中,以18个故障站点作为参考标准,计算误判数和漏判数,进而分析各类参数。
3.1 阀值系数k1、k2的分析
根据定义1可知:k1、k2分别控制异常大值和异常小值可疑的站点数。取N=50[7],对k1、k2取不同值的情况进行分析(见表1),其中结果表示式为:可疑站点(误判,漏判)。站点数与k1、k2的关系见图2、图3。

表1 k1、k2取不同值的分析结果
分析表1、图2和图3可知:漏判站点数与k1未呈相关关系,而可疑站点数和误判站点数总体与k1呈负相关关系,但当k1大于某个值时,两者固定不变;漏判站点数随着k2的增大而增多,但当k2大于某个值时,则保持不变 (全部漏判,算法失效),而可疑站点数和误判站点数与k2的关系类似于k1的关系。
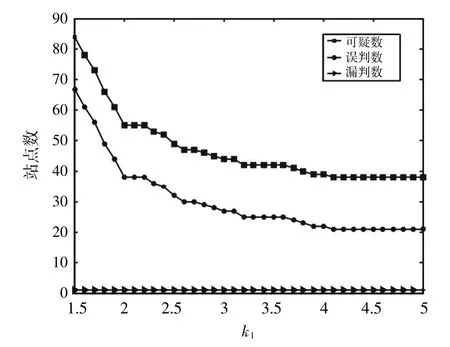
图2 站点数与k1的关系图(k2=2.0)

图3 站点数与k2的关系图(k1=4.1)
从以上分析发现误判和漏判的站点具有以下特征:站点数据偏大值,而根据它所选的样本均值偏小,且均差也小;漏判的站点具有的特性恰好与误判的特性相反,即站点数据偏小值,故在假设标准差稳定的前提下,误判的站点多数为大值,漏判的站点多数为小值。故对于阀值系数k1可稍取偏大值,反之k2可取稍小值,如k1=3.6和k2=1.8,并非一定依据标准莱因达准则 (k1=k2=3)。
出现以上结果主要因为在此次实证数据中,故障站点全部为异常偏小值,但这不能成为定律,在实际中,也有可能某些站点因为故障出现异常大值。
3.2 聚类水平N的分析
“莱因达”准则的前提是在分析范围内要有一定数量的样本数据。如果N越小,样本集合偏少,则漏判概率较高;反之,N越大,样本集合过大,则样本之间的相关性越小,算法的失效概率越高,且N越大会导致算法运算的时间越长。由以上的分析可知,取k1=3.6、k2=1.8时,算法的效果最好(见表2,图4)。

表2 k1=3.6、k2=1.8时N取不同值的分析表

图4 k1=3.6、k2=1.8时站点数与N之间的关系
分析表2、图4可知:随着N增大,算法开始收敛,基本不存在漏判站点,可疑站点的数目减少,但大于70后整体趋于稳定。
3.3 应用测试
为了验证以上参数的有效性、可用性,分别取k1=3.6、k2=1.8,N=70,对浙江省2011年3月1日20点至2011年3月31日20点的1 553个区域自动站观测的累计降水资料进行分析,结果为可疑度大于零的站点数为77个。考虑到2月份降雪后部分自动站出现故障,尚未修复,我们将37个可疑度大于0.5的站点数据不纳入分析的范围[8],得到的对比图如图5、图6。

图5 未经任何处理的原始资料分析效果

图6 经本文算法处理的资料分析效果
从图5和图6可知:利用原始数据绘制降水等值线色块图会在大值区出现 “梯度递减区域”、“较多逗点状小值”等不符合逻辑的问题,从而造成图形不可用、欠美观。而利用本文的算法可解决相关的问题。
4 结语
本文设计的算法在浙江气象部门经长时间的应用、服务,经过大量的数据测试,发现在区域大、时间长的降水过程效果较好,如:台风期、梅讯期等。而对于小尺度的降水或者局地大降水会偶尔失效。针对区域自动站数据应用问题,目前,气象部门尚未建立一套技术规范,本研究具有一定的科学性和实用性,对质量控制技术规范提供一种参考。
本文的算法中参数需大量的数据统计测试,才能投入业务使用,且参数仅仅适用于降水数据,对于其他气象要素的处理还有待于进一步的研究。
[1]Shafer M A,Fiebrich C A,Amdt S E,et al.Quality assurance procedures in the oklahoma mesonet[J].Journal of atmospheric and Oceanic Technology,2000,17:474-494.
[2]Eischeid J K,Baker C B,Karl T R,et al.The quality control of long-term climatological data using objective data analysis[J].Journal of Applied Meteorology, 1995,34(12):2787-2795.
[3]王新华,罗四维,刘小宁,等.国家级地面自动站A文件质量控制方法及软件开发[J].气象,2006,32(3):107-112.
[4]任芝花,刘小宁,杨文霞.极端异常气象资料的综合性质量控制与分析[J].气象学报,2005,63(4):526-533.
[5]王海军,杨志彪,杨代才,等.自动气象站实时资料自动质量控制方法及其应用[J].气象,2007,33(10):102-109.
[6]何平.剔除测量数据中异常值的若干方法[J].航空计测技术,1995,15(1):19-22.
[7]李学坤,李凤金.海洋水文气象实时数据质量控制[J].海洋预报,1997,14(3):71-76.
[8]陈正旭,封秀燕,王亚云.多岛屿地图上绘制气象要素等值线色块的自适应方法[J].气象科技,2009,37(3):356-359.
CHEN Zheng-xu1,WANG Jun-jiao2,HONG Yue-ying1
(1.Zhejiang Provincial Meteorological Information and Network Center,Hangzhou 310017,Zhejiang,China;2.Hangzhou Meteorological Bureau,Hangzhou 310008,Zhejiang,China)
In this paper,a new data processing method based on a kind of improved"PauTa" criterion is put forward for the treatment of real time precipitation data of regional automatic weather stations,to solve the problems occurred in related data applications.First,sample space is collected by Euclidean distance clustering,then the sample mean and the residuals are calculated,after that the definition for a suspicious degree is given,to calculate real suspicious degree of various sites.In the end,actual data in Zhejiang Province are used for parameter analysis,which proves the validity and practicability of the new method.
automatic station;quality control;real time information;"PauTa"rule

P415.12;O213.1
:A
:1673-0143(2012)03-0033-05
(责任编辑:强士端)
2011-10-18
浙江省气象局一般项目(2010YB02)
陈正旭 (1984—),男,工程师,硕士,研究方向:气象资料信息化处理和应用软件开发。
