三能级V型原子自发辐射的双色相位控制

2012-08-07石文星张立辉

江汉大学学报（自然科学版） 2012年3期

关键词：双色谱线能级

石文星，张立辉

（江汉大学物理与信息工程学院，湖北武汉 430056）

三能级V型原子自发辐射的双色相位控制

石文星，张立辉

（江汉大学物理与信息工程学院，湖北武汉 430056）

利用密度矩阵方程和量子回归理论研究了在一对双色场驱动下的三能级V型原子的自发辐射。研究结果表明，原子的自发辐射强烈依赖于这对双色场的相对相位差，而不依赖于双色场各自相位或相对相位。通过改变场的相对相位差，能够对原子的自发辐射实现选择性抑制或消除。

自发辐射；密度矩阵方程；共振荧光；量子回归理论

0 引言

原子自发辐射控制是激光物理与量子光学中最基本的问题。原子相干和量子干涉是控制自发辐射的基本机制，并由此产生了许多新颖现象，如电磁诱导透明[1］、无反转激光[2］、非线性增益[3］等。通常控制原子自发辐射的方法有两种，一种是利用外加相干场驱动与原子自发跃迁有相同能级的辅助跃迁[4-8］，量子干涉发生在原子跃迁之间。另一种是运用相干场激发原子自发跃迁。对于一个在近共振、强单色场激发下的二能级原子[9］，Mollow预言了其荧光谱是一个对称三峰结构。中心峰的频率与驱动场的频率相同，边峰位于中心峰两侧，且决定于驱动场的拉比频率。边峰强度只有中心峰强度的1/3，而线宽是中心峰的3/2。这个三峰谱的不同成份是由于不同的修饰态双线间的跃迁构成的。

近年来，人们已经更多地关注多色激发自发辐射的控制。Blind等[10］预测了一个被调制场驱动的原子可以产生荧光谱的新成分。Zhu等[11］用实验观察了二能级原子在强多色场激发下的这种荧光谱，发现谱线和Mollow谱在许多方面存在差异。这种谱线呈梳状结构，相邻峰的间距由调制频率决定。而对比于单色情况，边峰与中心峰的距离决定于拉比频率。Ficek等利用谐振分离和连分法[12-13］作出了更进一步的理论分析，同时显示如果增加调制场的数目将会导致谱线向Mollow三峰谱演化[14］。然而，这些研究主要限于二能级原子系统。最近，笔者的研究表明，多色激发三能级原子共振荧光具有强烈的相位依赖性[15-17］，通过改变激发场的相对相位差，原子的自发辐射谱线将被有选择性地抑制或完全抑制。

本文将进一步延伸前期的研究工作，考虑利用一对等频差双色场激发一个三能级V型原子系统，并关注双色场的相位对原子自发辐射的影响。

1 模型与方程

考虑一个由一对等频差双色场驱动的三能级V型原子系统，如图1所示。

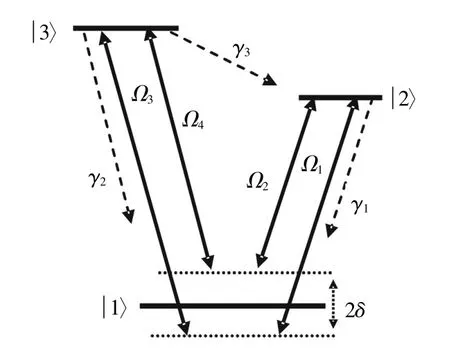
图1 V型三能级原子系统模型

双色场

在旋转波近似和偶极近似下，系统的约化密度矩阵方程为

其中系统哈密顿量H为

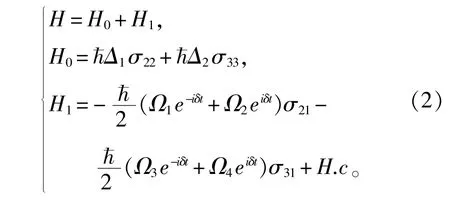
（2）式中已经定义了原子对场的失谐量Δ1=ω21-ωa，Δ2=ω31-ωb。其中ω21和ω31分别是原子跃迁的共振频率，ωa=（ω1+ω2）/2和ωb=（ω3+ω4）/2分别是耦合到跃迁和的光场的平均频率，2δ=ω1-ω2=ω3-ω4是相应驱动场的频率差。Ωj（j=1，2）和Ωk（k=3，4）是场与原子耦合的拉比频率，

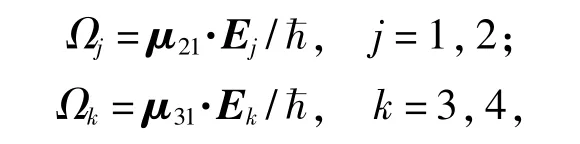
其中μ21和μ31是相应的电偶矩阵元。算符σij=对于i=j是原子的投影算符，而i≠j时为自旋算符。Lijρ描述了原子从能级到能级的衰减，形成

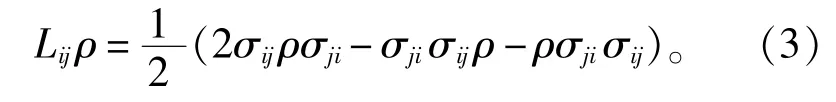
定义一个列矢量

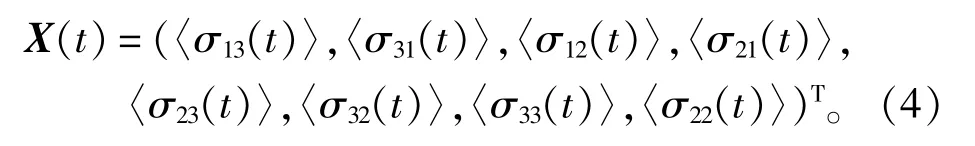
利用（1）～（4）式及封闭三能级原子系统的布居守恒条件ρ11+ρ22+ρ33=1，可得到原子算符期望值的运动方程

其中Q（t）是一个8×8矩阵，

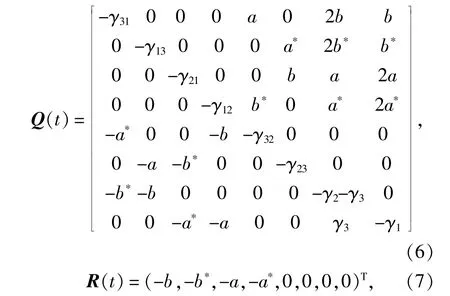
R（t）是一个列矢量，（6）式和（7）式中参数分别表示为

为了求解（5）式，使用谐振展开和矩阵反转，则密度矩阵元Xk（t）（k=1，2，…，8）展开为

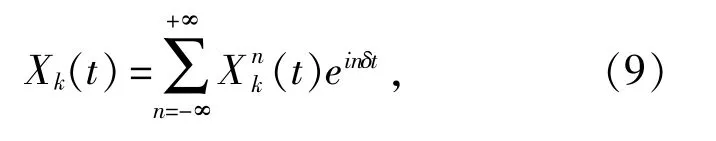
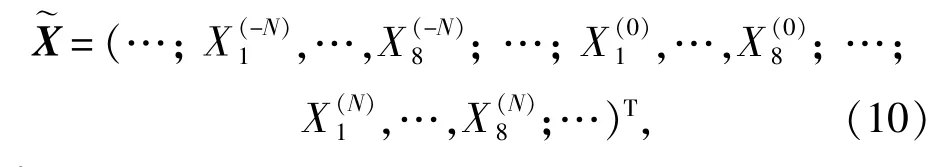
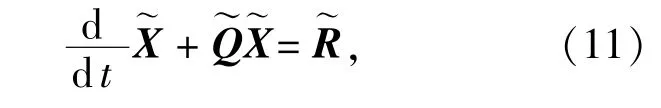
2 共振荧光谱

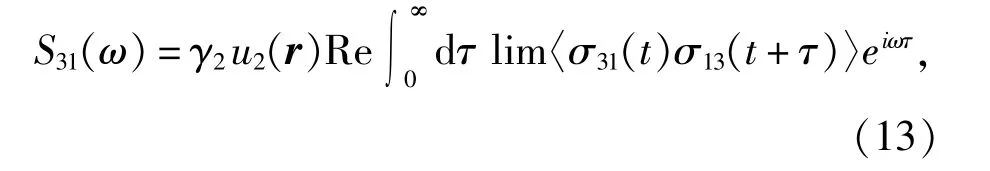
其中u2（r）=（3/8π）sin2θ2，θ2是位置矢量r与原子偶极矩矢量μ之间的夹角。（13）式中的关联函数可通过引入一个双时关联列矢量Y（t，τ）得到，列矢量Y（t，τ）的元为

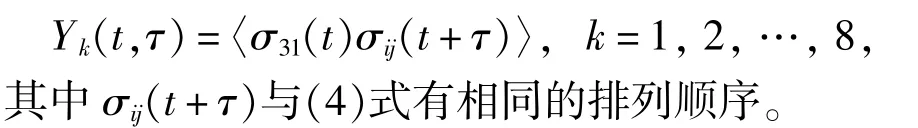
根据量子回归理论[9，18］，双时关联函数Y（t，τ）与单时关联函数X（t）具有相同的运动方程形式，即（5）式，除了将其中的列矢量R（t）替换成X2（t）R（t+τ）。然后利用前面相同的方法谐振展开，并进行傅里叶变换同时忽略自发辐射的相干部分，即傅里叶变换后含有δ函数部分。由于只有Y1（t，τ）=〈σ31（t）σ13（t+τ）〉的零阶分量对辐射的非相干荧光谱有贡献，则辐射的稳态共振荧光谱可表示为

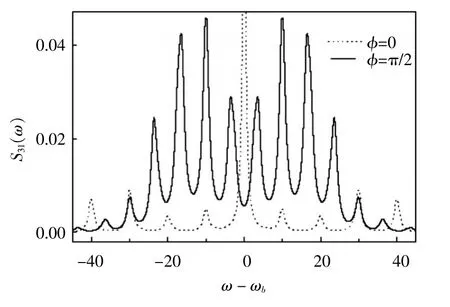
图2 |3〉→|1〉辐射的共振荧光谱

结果表明，在共振情况下，当φ=0时，荧光谱线相对于ω-ωb=0具有对称性，谱峰位于频率ω31±nδ（n为整数）位置处，相邻峰之间的距离为调制频率δ，且中心峰的强度最强。这种间距为δ的梳状结构谱线是由于驱动场与原子耦合导致能级分裂成梯状修饰态，如图3所示，修饰态能级间距为δ，即说明了相邻峰之间的间距为δ。

图3 共振修饰态能级图

并且，荧光谱强烈依赖于相干场分量的相对相位差φ。这是由于在修饰原子绘景中形成一个封闭环，相位依赖性出现在封闭环中。当改变相对相位差φ从0到π/2时，中心峰将被抑制且对称分裂成左右两个边峰，同时位于ω31±2nδ（n=1，2，…）的谱峰也将被抑制并分裂成两个谱峰，而成为谷。然而，位于频率ω31±（2n+1）δ（n=0，1，2，…）处的谱峰将不被抑制而仍然存在。此时，位于ω31±δ处的内边峰的强度加强并成为最大，但小于φ=0时中心峰的强度。

3 结语

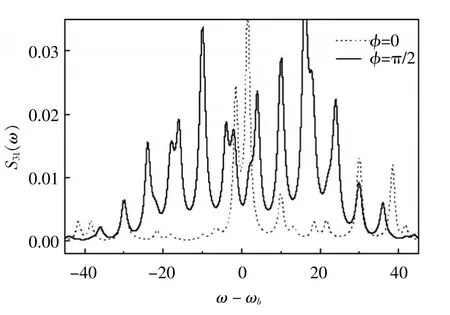
图4 |3〉→|1〉辐射的非共振荧光谱

本文研究了在一对相干双色场驱动下的V型三能级原子的荧光谱。研究表明，原子的自发辐射谱强烈依赖于双色场的相对相位差，而不依赖于双色场各自相位或相对相位。在共振条件下，原子的自发辐射谱呈现对称的梳状结构。在相对相位差为0时，中心峰位于驱动场的平均频率处，强度最强，相邻峰的间距为调制频率δ。当双色场的相对相位差从0改变到π/2时，荧光谱的中心峰被抑制并分裂成两个对称的边峰，同时位于偶边频处的谱峰亦被抑制并分裂成两个峰。通过改变驱动场的相对相位差，对原子的自发辐射谱实现了选择性抑制或消除，从而控制原子的自发辐射。

[1］Harris S E.Electromagnetically induced transparency [J］.Physics Today，1997，50（9）：36-42.

[2］Kocharovskaya O.Amplification and lasing without inversion[J］.Physics Report，1992，219（3/4/5/6）：175-190.

[3］Harris S E，Field J E，Imamoglu A.Nonlinear optical processesusing electromagnetically induced transparency[J］.Phys Rev Lett，1990，64（10）：1107-1110.

[4］Zhu S Y，Narducci L M，Scully M O.Quantum-mechanical interference effects in the spontaneous-emission spectrum of a driven atom[J］.Phys Rev A，1995，52（6）：4791-4802.

[5］Zhou P，Swain S.Ultranarrow spectral lines via quantum interference[J］.Phys Rev Lett，1996，77（19）：3995-3998.

[6］Paspalakis E，Knight P L.Phase control of spontaneous emission[J］.Phys Rev Lett，1998，81（2）：293-296.

[7］Keitel C H.Narrowing spontaneous emission without intensity reduction[J］.Phys Rev Lett，1999，83（7）：1307-1310.

[8］Ghafoor F，Zhu S Y，Zubairy M S.Amplitude and phase control of spontaneous emission[J］.Phys Rev A，2000，62（1）：013811-013817.

[9］Mollow B R.Power spectrum of light scattered by twolevel systems[J］.Phys Rev，1969，188（5）：1969-1975.

[10］Blind B，Fontana P R，Thomann P.Resonance fluorescence spectrum of intense amplitude modulated laser light[J］.J Phys B：At Mol Phys，1980，13（14）：2717-2727.

[11］Zhu Y F，Wu Q L，Lezama A，et al.Resonance fluorescence of two-level atoms under strong bichromatic excitation[J］.Phys Rev A，1990，41（11）：6574-6576.

[12］Ficek Z，Freedhoff H S.Resonance-fluorescence and absorption spectra of a two-level atom driven by a strong bichromatic field[J］.Phys Rev A，1993，48（4）：3092-3104.

[13］Aronstein D L，Bennink R S，Boyd R W，et al.Comment on“Resonance-fluorescence and absorption spectra of a two-level atom driven by a strong bichromatic field”[J］.Phys Rev A，2002，65（6）：067401-067405.

[14］Ficek Z，Seke J，Soldatov A V，et al.Fluorescence spectrum of a two-level atom driven by a multiple modulated field[J］.Phys Rev A，2001，64（1）：013813-013822.

[15］Hu X M，Shi W X，Xu Q，et al.Phase control of spontaneous emission by cascade bichromatic excitation [J］.Phys Lett A，2006，352（6）：543-549.

[16］Hu X M，Xu Q，Li J Y，et al.Bichromatic and trichromatic manipulation of spontaneous emission in a three-level Λ system [J］.Optics Communications，2006，260（1）：196-202.

[17］Li X X，Hu X M，Shi W X，et al.Phase control of spontaneous emission of a three-level atom in two bichromatic fields[J］.Chin Phys Lett，2006，23（2）：340-343.

[18］Narducci L M，Scully M O，Oppo G L，et al.Spontaneous emission and absorption properties of a driven three-level system[J］.Phys Rev A，1990，42（3）：1630-1649.

SHI Wen-xing，ZHANG Li-hui
（School of Physics and Information Engineering，Jianghan University，Wuhan 430056，Hubei，China）

Spontaneous emission of a three-level V-type atom driven by a pair of bichromatic fields on the basis of density matrix equation and quantum regression theories are studied.The results show that the spontaneous emission depends strongly on the difference between the relative phases of two bichromatic fields，without depending on the respective phase or relative phase.Selective elimination of the spontaneous emission can be achieved simply by varying the relative phase difference.

spontaneous emission；density matrix equation；resonance fluorescence；quantum regression theorem