构造零和区分器的新方法

董乐，吴文玲，吴双，邹剑

(1. 中国科学院 软件研究所，北京 100190；2. 中国科学院 研究生院，北京 100190)

1 引言

2001年，AES[1]被美国国家标准技术研究所（NIST）颁布为新的加密标准，其结构被密码工作者广为研究。随着RFID标签、智能卡和无线传感器等智能设备的推广，轻量级杂凑函数的设计成为近年热点之一。在2011年美洲密码年会上发布的、采用类似AES结构置换的PHOTON[2,3]族杂凑函数就是其中的一个。而在近年来举办的 SHA-3竞赛中，很多算法也都有和AES相似的结构或者设计理念，包括进入最终轮的JH[4]算法，其核心置换就采用了多维AES设计理念。这些与AES有相似结构的置换通常被称为AES类置换。

PHOTON杂凑函数族是由J Guo等设计，它采用了AES类置换。设计者在设计文档中给出了几种区分器攻击[2]。其中反弹区分器可以攻击到8轮，积分区分器可以攻击到 7轮。除此之外，基于对代数次数的估计，零和区分器可以对其中4个版本攻击到全轮12轮，对采用8bit S盒的版本攻击到8轮。

JH杂凑函数是进入SHA-3竞赛最终轮的5个算法之一，由学者H Wu独立设计。该杂凑函数采用了一种新的压缩函数结构。除此之外，在其轮函数的设计中，还采用了广义AES的设计理念。对于JH算法，V Rijmen等利用反弹攻击的思想，构造了杂凑函数16轮的半自由起始碰撞，和22轮压缩函数的半自由起始近似碰撞[5]。在2010年的SHA-3第2次会议上，M S Turan等以可实现的223.24的时间复杂度，构造了10轮压缩函数的半自由起始近似碰撞[6]。在 2011年的美洲密码年会上，N-Plasencia将 V Rijmen等的22轮半自由起始近似碰撞的时间和空间复杂度均降低至 295[7]。除此之外，在文献[8]中，C Boura等对JH置换的代数次数进行了新的估计，得出8轮置换的代数次数至多为409, PHOTON2个置换和JH的现有攻击比较如表1所示。

1994年，来学嘉教授提出了离散函数“高阶微分”的概念[9]，此后高阶差分[10]便成为分组密码分析的一个有力的工具。2009年，学者J P Aumasson基于对 3个 SHA-3候选算法 KECCAK、Luffa和Hamsi的区分攻击，提出了构造“零和区分器”[11]的攻击方式，这种区分器的构造便是基于算法的高阶差分性质。2010年，C Boura和A Canteaut等发现迭代置换的一些特殊性质[12]，并将其应用于KECCAK-f和Hamsi-256。而后，C Boura等改进了此方法，并构造出来全轮的KECCAK-f置换的零和区分器[13]。除此之外，J P Aumasson等人还给出了Hamsi-256的一些“2i-和”区分器[14]。

本文应用高阶积分攻击和高阶差分攻击，针对AES类置换的扩散性质，提出一种构造零和区分器的新方法。并对PHOTON和JH中的置换，构造出由高阶积分路径和高阶差分路径组成的组合路径。基于这些路径，建立了JH的31.5轮核心函数的“零和区分器”，并改进了 PHOTON杂凑函数族中 2个置换的“零和区分器”。

2 PHOTON杂凑函数族与JH杂凑函数

本节对PHOTON杂凑函数族和JH杂凑函数进行介绍，其中主要介绍它们所使用的置换。

2.1 PHOTON杂凑函数族

PHOTON[2,3]杂凑函数族是由Guo J等人设计的一族轻量级杂凑函数，正式发布于 2011年美洲密码年会。PHOTON采用了2个主要技术：1）扩展的海绵结构；2）AES类置换。

海绵函数是一种由固定置换构建杂凑函数的新选择。为了增加灵活性，PHOTON采用了扩展的海绵结构。它允许每次置换P之后的“比特榨取”时析出比特的个数可以与“比特吸收”时吸收的比特个数不相同，这样可以减少“比特榨取”过程的时间。

PHOTON的内部置换使用的是一个AES类函数。中间状态可被表示为一个sb2bit大小的b×b的方阵，本文中称状态矩阵中的元素为“单元”，这里s表示每个单元的大小，即每个S盒的大小,b表示每行（或者每列）包含的单元个数。PHOTON的每一轮包含4个基本运算，如图1所示。

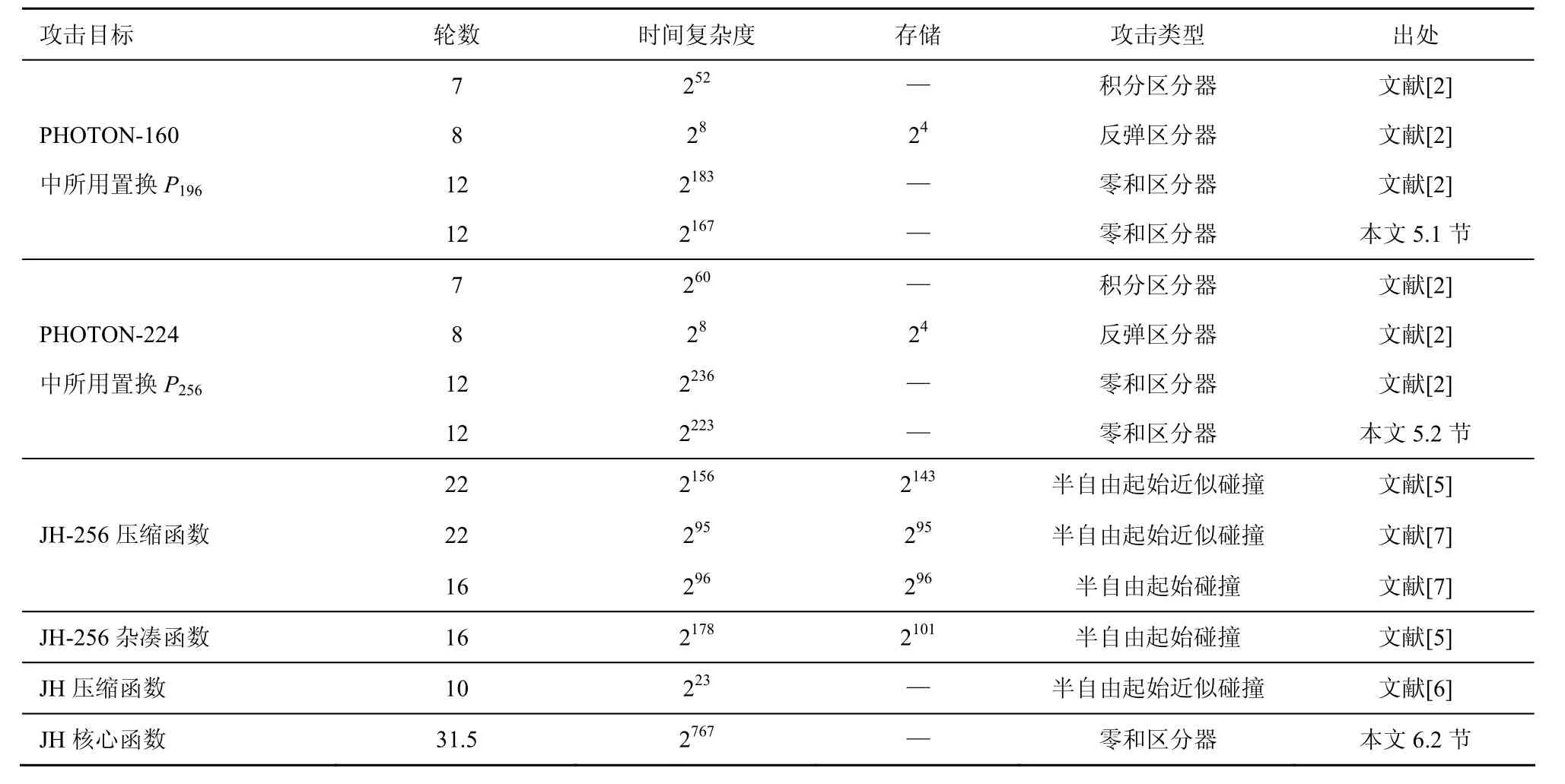
表1 PHOTON 2个置换和JH的现有攻击比较

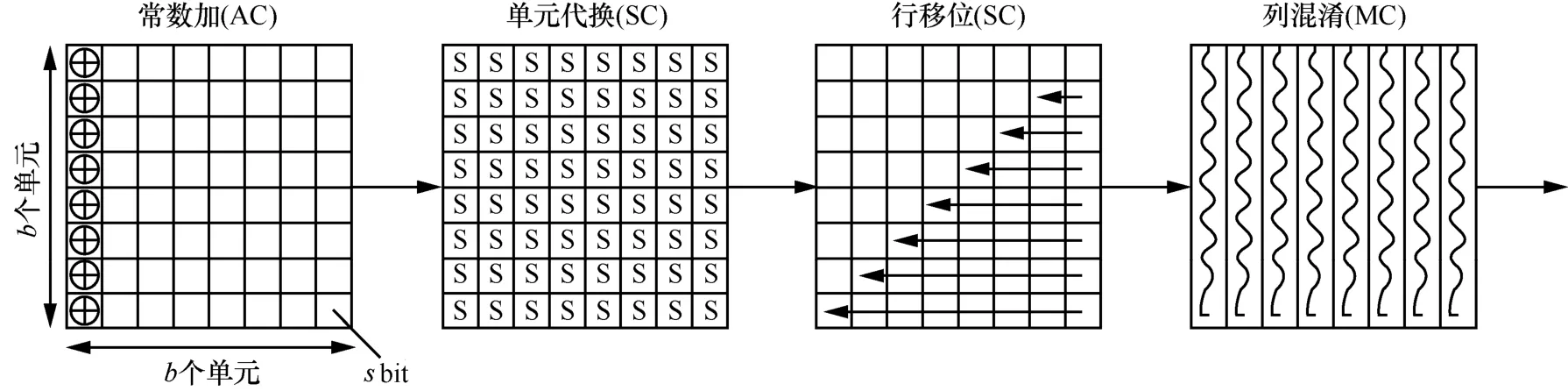
图1 PHOTON置换P256的一轮

1) 常数加(AC)：状态中第一列的每个单元异或上一个常数，以破坏列之间的对称性，并区分置换的每一轮。

2) 单元代换(SC)：2种S盒被用来构建置换层，PRESENT算法中的4bit S盒，与AES算法中的8bit S盒。其中，8bit S盒只用在PHOTON函数族的一个置换中。

3) 行移位(SR)：与AES的行移位非常相似。简单地说，就是第i行向左循环移动i个单元，i从0开始。

4) 列混淆(MC)：为了降低实现代价，PHOTON的混淆层使用一个含很多0的矩阵，并用一系列的迭代更新列向量。这个过程相当于乘以一个 MDS矩阵。

这样，PHOTON的轮函数可以表示为

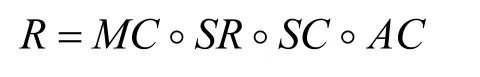
PHOTON杂凑函数族共包含5个成员，它们使用的内部置换分别为P100、P144、P196、P256和P288。表 2给出这些置换内部状态大小t、每行或者每列的单元个数b、S盒大小s和轮数Nr。

从表中可知，除了最后一个置换，其余置换都采用了4×4的S盒。此外，每一个置换的轮数都是12。文献[2]还给出随着轮数增加，5个版本的置换代数次数的上界。其中5轮P196和P256置换的代数次数上界分别为157和197。

表2 5个内部置换的参数

使用 PHOTON对一个消息进行杂凑，首先填充消息，使得填充之后的长度为每次吸收比特数 r的倍数。而后将它们分为r比特的块 M1,… ,MN。每一次吸收，状态Si吸收消息块Mi，然后进入置换Pt更新状态。可以用下式表示。

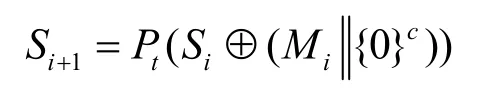
所有消息块都被吸收之后，便开始榨取部分。摘要值就是将每次r′比特的输出连结起来，直到达到所需长度[2,3]。

2.2 JH杂凑函数

JH是进入SHA-3竞赛最终轮的5个杂凑函数之一。它是一个迭代型的杂凑函数，其设计理念有2个重要部分：1）多维AES的设计；2）一个新的压缩函数结构。JH的压缩函数采用一种新的结构，如图2所示。

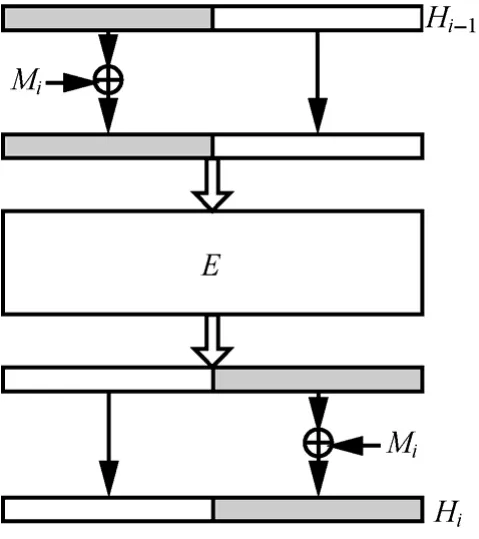
图2 JH的压缩函数结构

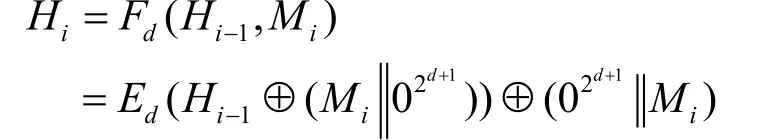
其中，Fd为压缩函数，Ed为一个双射函数。本文中称Ed为JH的核心函数。d表示JH状态的维数，即其状态可以记为一个d维的矩阵。笔者推荐d=8。

JH杂凑函数处理的消息长度需要是 512bit的倍数，最后生成的摘要长度为224bit、256bit、384bit或512bit。为了使处理的消息比特长度为512的倍数，需对消息按一定规则进行填充，填充后的消息被分为N个512bit的块， M1,M2,… ,MN。

核心函数中，2d+2个输入首先用“比特切片”的方式分为2d个4bit大小的“半字节”。而后，这些半字节经过包含6(d - 1 )轮的轮函数Rd。最后再应用开始的“比特切片”的逆变换。轮函数Rd共包含3种运算。

1) S盒：JH有2个4×4的S盒，每次使用哪一个取决于轮常数。

2) 线性扩散层：运算L将2个4bit的字(A,B)变为2个4bit字(C,D)，运算规则为

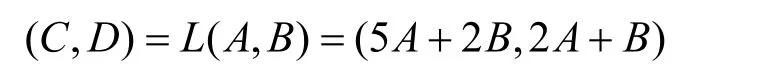
3) 置换 Pd：交换状态中“半字节”的次序，与AES轮函数中的行移位（shiftrows）运算相似。

JH的轮函数Rd的一轮可以用Pd◦L◦ S来表示。以d=4时为例，设 a1, … ,a15和b1,… ,b15分别为一轮的输入输出，则轮函数R4的一轮可以用图3来表示。

笔者推荐的版本中维数为 8，所以核心函数的总轮数为42。此外，状态大小为1 024bit，生成摘要的时候截取最后一个链值HN的一部分比特[4]。

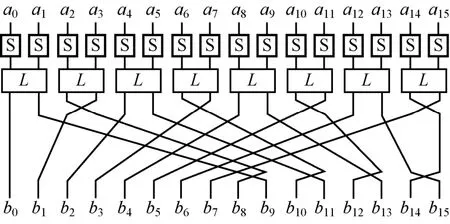
图3 R4的一轮

3 高阶差分与零和区分器

3.1 高阶差分

1994年，学者来学嘉给出了密码函数的微分的定义[9]。

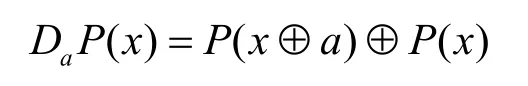
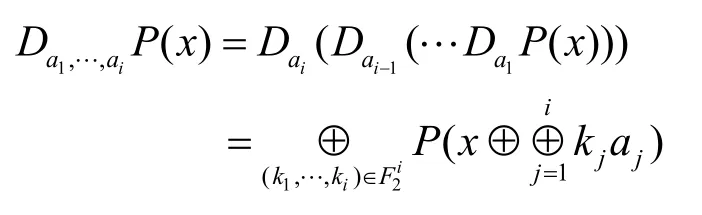
而P在点a1,…,ai处的i阶微分定义为对于任意的上的m维子空间V，P在V上的m阶微分为函数

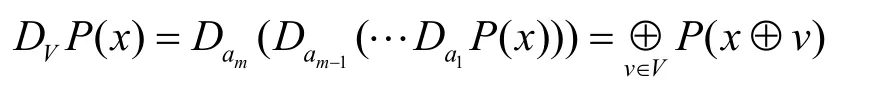
其中， a1,… ,am为V的一组基。

一个函数的一阶微分的代数次数有性质deg(DaP( x) )≤ deg P ( x)-1。所以，对于任意的(deg P + 1 )维的子空间 V或者是任意的(deg P +1)个点 a1, … ,adegP+1，置换P的(deg P + 1 )阶微分为0。

3.2 积分攻击

积分攻击[15～18]是一种基于字节的分组密码攻击方法。这种攻击的基本思想是：考虑一些值和的传播性质，并利用这些性质来验证所猜测密钥。

攻击中，一些明文字节被选定为常数，记为C，其他字节，一般称为活跃字节，取遍所有的256个值，这些字节记为A。对于活跃字节来说，通过S盒变换之后仍然是活跃的。也就是说，活跃字节通过S盒之后的像仍然取遍所有的256个值。而且通过轮常数加运算之后，活跃性也不变。如果通过行移位运算，活跃字节的位置会发生变化。

文献[15,17]还提出了高阶积分的思想。和原始的积分攻击不同，高阶积分的起始点为多个活跃字节，这些字节之间独立，它们在通过开始的几轮S盒和线性扩散层之后仍然是活跃的。原因为S盒和线性扩散层都是置换，只要输入取遍所有情况，输出一定也可以取遍。当然，利用积分攻击也可以攻击基于“半字节”的算法。

3.3 零和区分器

零和区分器由学者J P Aumasson于2009年提出[11]。

定义2 设F为一个 F2n上的函数。如果F的输入集， { x1, … ,xK} ⊂ F2n，满足下面2个条件。

1) 所有这些元素的和为0。

2) 所有这些元素在F下的像的和为0。则称其为F的大小为K的零和。

本文以高阶差分为工具，来构造某些密码函数的零和区分器。由前面的高阶差分的性质，如果已知一个 F2n上的置换P的代数次数的上界l。在P的输入中任意选择 n - ( l + 1 )个比特位置，选定这些比特的值，遍历剩下的(l + 1 )个比特（称其为活跃比特）的所有可以取到的值。则由高阶差分性质，这2l+1个输入的输出之和为0。

对于由轮函数迭代构成的置换，这里用P = Rr◦…◦R1来表示，选择合适的整数 t，1≤t≤r，将置换P分成2部分，Fr-t=Rr◦…◦Rt+1和令

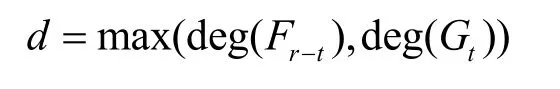
如果中间状态含有的比特数大于d+1，可以在第t轮的输出状态中选择d+1bit作为活跃比特，向两边计算，最后在两端得到平衡的状态，即输入输出的和都为0（如图4所示）。

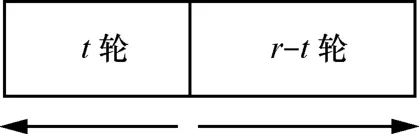
图4 零和攻击结构

4 构造零和区分器的新方法

本节介绍一种针对 AES类置换，构造零和区分器的新方法。这种方法组合高阶积分攻击和高阶差分攻击，针对 AES类置换的扩散特点，构造一条由高阶积分路径和高阶差分路径组合而成的组合路径。

本文所研究的AES类置换，状态可以表示成一个方阵，轮函数使用的是SP结构，各单元需要平行独立地通过S盒，然后一列（或者一行）再进入一个线性扩散层进行混淆。具体来说，考虑F为一个上的由轮函数迭代而成的AES类置换，其状态为一个d维方阵，状态中单元大小为sbit，每行（或者每列）含有b个单元，即状态大小为sbdbit。轮函数使用的SP结构满足，状态先通过多个置换S盒并置的代换层，然后再进入一个一维的线性扩散层P。除此之外还有一个交换单元位置的移位运算和一个常数加运算（如果没有常数加，可以看作加上全为0的常数）。设P的分支数达到最大的b+1，则对于这类置换，有下面结果。

命题1 置换F如上所述，则选定状态中的一个单元，达到完全扩散（即某中间状态中每个单元都与所选单元相关）至少需要d轮；同样地，逆向计算达到完全扩散也至少需要d轮。

证明 由于线性扩散层只在一维（即一行或者一列）上进行，而其分支数达到最大的b+1，所以经过一轮运算，状态矩阵中有b个单元与所选单元相关。考虑到单元换位运算，两轮之后至多有 b2个单元与所选单元相关。由此继续推导，则经过 i轮运算，至多有bi个单元与所选单元相关。所以，由于状态为一个d维方阵，若使得所有bd个单元与所选单元相关，至少需要d轮。逆向结果利用同样证明过程可得。证毕。

命题2 置换F如上所述，设其d轮可达到完全扩散。选定状态中的一个单元，则从此状态出发，第d–1轮的输出状态中有 bd-1个单元与所选单元相关，即第d轮的S盒计算中有1 b与其相关；同样地，逆向计算第d–1轮的输出状态中也有 bd-1个单元与所选单元相关，但逆向第d轮的S盒全部与其相关。

证明 由于使用的一维线性扩散层，而达到完全扩散需要d轮，所以d–1轮之后能且只能有 bd-1个单元与所选单元相关。再进入第d轮的S盒层时有bd-1个S盒计算与其相关。而对于逆向计算，易知同样有d–1轮之后能且只能有 bd-1个单元与所选单元相关。但是，由于逆向计算第d轮时，先进入线性扩散层P，然后进入S盒层，所以逆向第d轮的S盒全部与其相关。证毕。

命题3 置换F如上所述，并且d轮可达到完全扩散。则至多需要选择 bd-1个单元作为高阶积分攻击中的活跃单元，即取遍这些单元中的所有2s(bd-1)种情况，剩余的一个单元取定值，记为 Ci，能够使得：

1) 正向计算，第 d轮的 S盒层的输出中，有(b - 1 )bd-1个单元是活跃且独立的（相互独立，并且与其他 bd-1个单元也无关，下文中的“独立”也代表同一意思）；

2) 逆向计算，第d–1轮的S盒层的输出中，有(b - 1 )bd-1个单元是活跃且独立的。

证明 由命题2可知，正向计算第d–1轮，有bd-1个单元与取定值的单元 Ci相关。又由于S盒层和一维线性扩散层，包括单元换位运算和常数加运算，都是置换，即双射，所以其他的 (b - 1 )bd-1个单元是活跃且独立的。这些单元在经过第d轮的S盒层后，仍然是活跃且独立的。

而对于逆向计算，由于S盒层在扩散层P之后，所以只能保证在第 d–1轮的 S盒层的输出中，有(b - 1 )bd-1个单元是活跃且独立的。证毕。

对于某个具体算法，可能不必选择 bd-1个活跃单元，有时更少的活跃单元也可以得到同样的结果。以已知密钥的AES为例，取15个字节为活跃字节，剩下的一个字节取定值，则通过第2轮的S盒层之后，仍然有 12个字节活跃且独立。但是事实上，取状态矩阵中主对角线之外的 12个字节为活跃字节，也能达到这个结果。

基于这些结果，针对上述 d轮可完全扩散的AES类置换，可以利用高阶积分攻击和高阶差分攻击思想，用如下步骤构造零和区分器。

1) 选择一个中间状态，称其为起始状态，在此状态中选择一个单元。对此单元任选一个定值，而对其他单元取遍所有的 2s(bd-1)种情况，也就是说，其他单元为高阶积分攻击中的活跃单元。

2) 由命题3，正向计算第d轮的S盒层之后有(b - 1 )bd-1个单元是活跃且独立的。另一方面，可以保证在逆向计算d-1轮后，有 (b - 1 )bd-1个单元是活跃且独立的。这样就建立了一条(2d-1.5)轮的高阶积分路径。

3) 计算若干轮正向迭代后的代数次数。如果j轮迭代后的代数次数小于 s ( b - 1 )bd-1，而 j+1轮代数次数大于等于 s ( b - 1 )bd-1，则以上述高阶积分路径的终点作为起始点，进行j轮的高阶差分攻击。虽然高阶差分路径是从第 2)步剩下的一个 P置换（0.5轮）开始，但是由于P置换是线性的，也就是说代数次数为 1，不影响高阶差分路径的代数次数，所以在高阶差分路径的终点得到平衡状态。逆向的攻击和正向相似。

这样就得到了一个(2 d -1 + j+ j′)轮的零和区分器。图5表示了整个攻击过程。

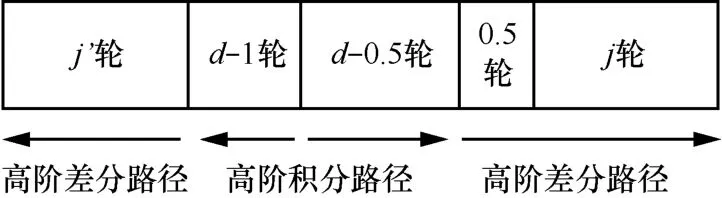
图5 改进的零和攻击结构

值得注意的是，针对某些具体算法，有时可以选取具有更少活跃单元的中间起始状态，来降低攻击的复杂度。但是，有些情况更少的活跃单元可能会导致攻击的轮数略有减少。

5 2个PHOTON置换的改进零和攻击

PHOTON杂凑函数族中采用的置换为 d=2维AES结构，S盒层采用的是PRESENT的4bit S盒，或者是AES的8bit S盒，所以s=4或s=8。状态中单元为字节或半字节，个数b2分别为25，36，49，64和 36。扩散层分支数均达到最大，并且经过 2轮可以达到完全扩散。则在中间可以构造一条1+1.5=2.5轮的高阶积分路径，并且在积分路径的两端保证有sd(d–1)个比特活跃。这样可以对置换P196和P256进行13轮的零和攻击。但是，这2个置换全轮只有 12轮，基于这个考虑，如果选择合适的单元作为活跃单元，可以在攻击轮数减少一轮的情况下，大大降低攻击的复杂度。

5.1 对P196的改进零和攻击

P196采用4bit S盒，状态中含有72=49个“半字节”。攻击中每一步攻击的轮数为

具体攻击过程如下。

1) 在整个12轮置换中，选择第6轮的输出作为起始状态，并选择状态中的前6列活跃，即选择最后1列为定值，遍历前6列的2168种情况（如图6所示，灰色表示活跃半字节，白色表示非活跃半字节，取图中MC的输出，即第6轮的输出为起始状态）。

2) 正向计算，这6个活跃列在通过第7轮的S盒之后仍然是活跃且独立的，后面的行移位和线性扩散层归到高阶差分路径中去，并不影响其代数次数；而逆向计算，由于列混淆运算是一个置换，所以，这6列在通过第6轮的列混淆的逆之后仍然活跃且独立，通过行移位的逆之后活跃半字节只是位置发生变化，通过S盒层的逆之后仍然有42个活跃且独立的半字节，包含168bit。

3) 由5轮代数次数至多为157，并且其逆函数次数与其相同可知，从168个活跃比特出发，经过5轮之后的状态是平衡的。

这样就以2168的复杂度，构造了一个P196的零和区分器。

5.2 对P256的改进零和攻击

P256采用4bit S盒，状态中含有82=64个“半字节”。每一步攻击的轮数与上述对P196的攻击中的轮数相同。攻击过程也是从选择第6轮输出开始，选择前7列活跃，则正向计算0.5轮，逆向计算1轮之后仍然有224个活跃比特，而其5轮的代数次数至多为 197，所以可以在高阶差分路径的两端得到平衡状态。

这样就以2224的复杂度，构造了一个P256的零和区分器。

图6 P196零和攻击的中间1.5轮

6 JH核心函数的零和区分器

本节对 JH的核心函数进行零和攻击。首先分析了一下4维的核心函数，然后在此基础上得到8维的分析结果。

JH核心函数的轮函数是一个广义的AES构造。它以4bit的“半字节”为单元，先通过一个S盒层提供非线性性，然后是4bit元素进行两两线性混淆，最后是一个元素换位。这里的S盒是4bit入、4bit出的平衡S盒。线性扩散层是一个双射，分支数为2。考虑积分攻击，2个活跃且独立的“半字节”通过此扩散层，仍然是2个活跃且独立的“半字节”。如果一个活跃，一个非活跃或者2个活跃不独立的“半字节”通过此扩散层，则输出2个“半字节”不能达到活跃且独立的要求。

这里，参数b=2，s=4，对于一个d维状态来说，共有2d个“半字节”，状态大小为2d+2bit，并且正向和逆向达到完全扩散均需要d轮，和状态的维数相等。

6.1 4维JH核心函数E4的零和攻击

对4维JH核心函数E4，可以构造一个15轮的零和区分器（总轮数为18）。攻击同样包含3个步骤，每一步攻击的轮数为

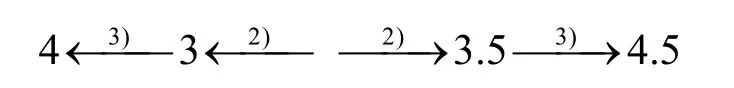
具体攻击过程如下。

1) 根据第4节的方法，首先需要在第7轮的输出状态中选定一个“半字节”的值，遍历其他 15个“半字节”的值。这样在第10轮中S盒层的输出状态和第4轮的输出状态中，存在 ( 2 - 1 )24-1=8个活跃且独立的“半字节”。但是，由 JH轮函数的扩散特点，如果选择后8个“半字节”作为活跃“半字节”，正向计算，在第10轮S盒层输出的第2、4、6、8、9、11、13、15个“半字节”活跃且独立，个数仍然是8个；并且，如果选择第2、4、6、8、9、11、13、15个“半字节”作为活跃“半字节”，逆向计算3轮，在第4轮的输出状态中，后8个“半字节”活跃且独立。综合正向逆向考虑，在第7轮的输出状态中，只需选择后8个“半字节”和前 8个“半字节”中的第 2、4、6、8个作为活跃“半字节”，即可保证在第4轮的输出状态和第10轮的S盒层输出中存在8个活跃且独立的“半字节”，共包含32个比特。如图7所示，活跃且独立“半字节”用加粗的黑线表示。需要注意的是，只有2个粗黑线入的扩散层L才能保证2个粗黑线出，即满足活跃且独立的条件，其他情况均不行。

2) 正向计算3.5轮，逆向计算3轮，在第10轮中S盒层的输出和第4轮的输出，得到含有8个活跃且独立的“半字节”状态，共包含32bit。需要注意的是，剩下的8个“非活跃半字节”的值并不是固定的。总的来说，它们也有 248-32= 216种情况，但是，由于它们和8个“活跃半字节”是独立的，所以，对于每一种情况，8个“活跃半字节”都会取遍所有的 232种情况。如果每一种情况都会得到平衡状态，即和为0的状态，则综合起来考虑，和仍然为0，仍然为平衡状态。

3) 由文献[8]中Boura C等给出的结果，4轮的JH的代数次数至多是25，所以加上次数为1的半轮，再正向计算4.5轮；此外，还可以再逆向计算4轮。

综上所述，以 248的复杂度（事实上，只需选择全部“半字节”的 3/4作为活跃“半字节”即可），对轮函数R4构造一个15轮的零和区分器。事实上，由于逆向计算先进入一个线性扩散层 L，再进入 S盒层，所以可以在最左端再加上0.5轮，得到和原来4轮逆向函数的代数次数相同的4.5轮逆向函数，使得攻击复杂度不变，而攻击轮数增加0.5轮。

和轮函数R4相比，核心函数E4多了开始的“比特切片”和最后的“比特切片”逆运算。这只会变换比特的位置，不影响其平衡性。至此，得到了核心函数E4的15.5轮的零和区分器。

6.2 8维JH核心函数E8的零和攻击

JH的推荐版本中，维数d=8。参照4维版本的攻击过程对其进行攻击，构造一个 31轮的零和区分器（总轮数为42），每一步的攻击轮数为

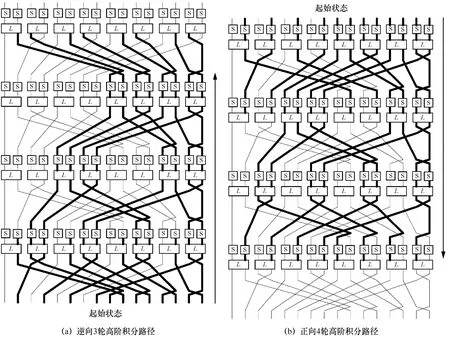
图7 P4构造的7轮高阶积分路径

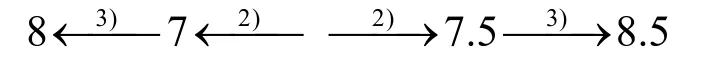
根据4维版本的攻击步骤，首先需要在第15轮的输出状态中，选择个活跃“半字节”，其他的取为定值。分别进行正向和逆向计算，在第23轮中S盒层的输出状态，和第8轮的输出状态中，有(2 - 1 )× 28-1= 1 28个活跃且独立的“半字节”，共包含512bit。这样就可以以积分路径的终点作为起始点，来构造高阶差分路径。8轮的JH核心函数的代数次数至多是 409[8]，所以用具有 512个活跃比特的状态作为起始点，8轮之后必为平衡状态。加上次数为1的半轮，可以正向计算8.5轮；此外，还可以再逆向计算8轮。

而根据零和区分器特点，在构造的时候只需要找到其所需的输入即可，也就是说，只需进行逆向计算，这样可以节省大约一半的时间，所以其时间复杂度为2767。

在SHA-3竞赛第1、第2轮中，JH采用的轮数为5(d-1)+0.5，对其轻量级版本，即d=4时的核心函数来说，其轮数为15.5，而本文中构造的零和区分器也可以区分4.5+3+4+4=15.5轮。基于安全性考量，本文在第3轮将轮数增加到6(d-1)。

7 结束语

本文根据AES类置换的特点，提出了一种针对这类置换构造零和区分器的新方法。这种方法是高阶积分攻击和高阶差分攻击的组合。如果有若干轮轮函数代数次数上界的一个估计，则可以根据此上界，在中间先构造一条高阶积分路径，然后以这条高阶积分路径的2个终点作为起始点，再进行高阶差分攻击。

利用这一方法，对PHOTON算法中的2个置换进行零和攻击，分别以2168和2224的复杂度，构造了P196和P256的零和区分器。此外，还对JH中的置换进行零和攻击，以 2768的复杂度构造了 JH核心函数的31.5轮零和区分器。如何构造出轮数更多的区分器值得将来的研究和关注。

[1] JOAN D, VINCENT R. The Design of Rijndael: AES—the Advanced Encryption Standard[M]. Springer-Verlag, 2002.

[2] GUO J, THOMAS P, AXEL P. The photon family of lightweight hash functions[EB/OL]. http://eprint.iacr.org/2011/609.pdf, 2011.

[3] GUO J, THOMAS P, AXEL P. The Photon family of lightweight hash functions[A]. Proc of the Advances in Cryptology-CAYPTO 2011[C].Santa Barbara, CA, USA, 2011. 222-239.

[4] WU H. The Hash Function JH[EB/OL]. http://icsd.i2r.a-star.edu.sg/staff/hongjun/jh/jh_round2.pdf, 2008.

[5] RIJMEN V, TOZ D, VANCI. Rebound attack on reduced-round versions of JH[A]. Proc of the Fast Software Encryption-FSE 2010[C].Seoul, Korea, 2010. 286-303.

[6] TURAN M-S, UYAN E. Practical near–collisions for reduced round blake, fugue, Hamsi and JH[EB/OL]. http://csrc.nist.gov/ groups/ST/hash/sha-3/Round2/Aug2010/documents/papers/TURAN_Paper_Erde ner.pdf, 2010.

[7] N-PLASENCIA M. How to improve rebound attacks[A]. Proc of the Advances in Cryptology-CAYPTO 2011[C]. Santa Barbara, CA, USA,2011. 188-205.

[8] BOURA C, CANTEAUT A. On the influence of the algebraic degree of F-1 on the algebraic degree of G circ F[EB/OL]. http://eprint.iacr.org/ 2011/503.pdf, 2011.

[9] LAI X J. Higher order derivatives and differential cryptanalysis[A].Proc of Symposium on Communication, Coding and Cryptography, in honor o] James L. Massey on the Occasion of His 60'th Birthday[C].Monte-Verita, Ascona, Switzerland, 1994. 10-13.

[10] KNUDSEN L R. Truncated and higher order differentials[A]. Proc of the Fast Software Encryption-FSE 1994[C]. Leuven, Belgium, 1995.196-211.

[11] AUMASSON J-P, MEIER W. Zero-sum distinguishers for reduced keccak-f and for the core functions of luffa and hamsi[EB/OL]. http://www.131002.net/data/papers/AM09.pdf, 2009.

[12] BOURA C, CANTEAUT A. Zero-sum distinguishers for iterated permutations and application to KECCAK-f and Hamsi-256[A]. Proc of the Selected Areas in Cryptography-SAC 2010[C]. Waterloo, Ontario, Canada, 2011. 1-17.

[13] BOURA C, CANTEAUT A, CANNIÈRE C D. Higher-order differential properties of Keccak and Luffa[A]. Proc of the Fast Software Encryption-FSE 2011[C]. Lyngby, Denmark, 2011. 252-269.

[14] AUMASSON J-P, KÄSPER E, KNUDSEN L R, et al. Distinguishers for the compression function and output transformation of hamsi-256[A].Proc of the Information Security and Privacy-ACISP 2010[C]. Sydney,Australia, 2010. 87-103.

[15] KNUDSEN L R, WAGNER D. Integral cryptanalysis[A]. Proc of the Fast Software Encryption-FSE 2002[C]. Leuven, Belgium, 2002.112-127.

[16] DAEMEN J, KNUDSEN L R, RIJMEN V. The block cipher square[A].Proc of the Fast Software Encryption-FSE 1997[C]. Haifa, Israel, 1997.149-165.

[17] FERGUSON N, KELSEY J, LUCKS S, et al. Improved cryptanalysis of rijndael[A]. Proc of the Fast Software Encryption-FSE 2000[C].New York, NY, USA, 2001. 213-230.

[18] GALICE S, MINIER M. Improving integral attacks against rijndael-256 up to 9 rounds[A]. Proc of the Progress in Cryptology – AFRICACRYPT 2008[C]. Casablanca, Morocco, 2008. 1-15.