针对随机伪操作的简单功耗分析攻击

王敏，吴震

（成都信息工程学院 网络工程学院，四川 成都 610225）

1 引言

功耗分析攻击是利用运算电路的功耗信息泄露，对密码芯片加解密过程的功耗进行分析，猜测出密码芯片加解密所使用密钥的一种攻击手段[1,2]。

在抵抗功耗分析攻击的各种策略中，使用随机动作来破坏功耗和密钥间的相关性是一种重要的方法，正确的使用这种技术确实能很好地达到抗功耗分析攻击目的。然而，错误的使用方式反而会使算法安全性大大下降。随机伪操作椭圆曲线密码标量乘算法就是这样的一个实例。

椭圆曲线密码（ECC, elliptic curve cryptography）是基于椭圆曲线数学的一种公钥密码。该算法与其他公钥密码算法相比具有比特强度高，计算速度快，存储空间小等特点，在资源受限的嵌入式系统（如智能卡）等安全领域广泛应用。

自从功耗分析攻击提出以后，公钥算法实现如何在兼顾效率的同时抵抗功耗分析攻击，成为密码学研究的一个重点。随机伪操作椭圆曲线标量乘算法[3]是在固定添加伪点加法算法（又称 double and add always算法）[4,5]基础上引入随机机制而形成的一种提高效率的改进型算法，该算法试图用随机性保持其抗简单功耗分析（SPA, simple power analysis）攻击能力的同时提高运算效率。但该类算法在设计实现中对随机性的使用存在一定缺陷，为提高效率而引入的随机伪操作反而可能成为 SPA攻击成功的决定因素。

下面从添加伪点加法算法的抗 SPA攻击原理入手，具体分析添加随机伪操作的椭圆曲线标量乘算法的缺陷及其多样本 SPA攻击实现方法，并给出实测结果，最后给出抗多样本SPA攻击的改进建议。

2 椭圆曲线密码算法的随机伪操作标量乘法

2.1 椭圆曲线密码算法的标量乘法

椭圆曲线密码算法的核心运算为标量乘kP的计算，而标量乘法运算过程中包含有密钥k的信息，因此对于标量乘法的功耗分析攻击成为了椭圆曲线密码算法重要的攻击点。

在标量乘实现算法中主要使用点加(QQP= + )和倍点( 2PP= ) 2种定义在椭圆曲线上的运算[6,7]，SPA攻击可利用这2种运算在功耗曲线上的不同形状，直接恢复出K值[3]。

2.2 添加伪点加法

针对标量乘的添加伪点加法是根据 SPA攻击原理，为了掩盖密钥k与运算间的操作相关性，对标量乘实现算法进行修改，使得当密钥k对应比特是“0”或“1”时，都进行点加和倍点2种运算，来达到掩盖密钥与运算间的操作相关性的目的，其具体实现算法、抗SPA攻击能力和算法效率见文献[3]。

2.3 随机伪操作法实现原理

文献[3]提出的随机伪操作法是将上述添加伪点加实现算法进行的修改，当密钥k对应比特为0时不再单纯地添加一次伪点加操作，而是随机添加一次伪操作，该伪操作为点加、倍点、无操作三者之一，并且为了既能提高抵抗SPA攻击能力，又能尽可能地减少效率损失，对添加伪操作各类型概率进行控制，将添加无操作的概率控制在50%左右，添加点加和倍点的概率总和控制在50%左右，随机伪操作法程序流程如图1所示。

算法原意是想利用随机伪操作来掩盖功耗曲线与密钥K之间的相关性，同时对固定添加伪点加的算法加以效率上的改进，详见文献[3]。然而，在下面的分析中可以看到，这种添加伪操作的方法如果没有其他防护措施的配合，实际上破坏了原固定添加伪点法的安全性，仅使用 SPA攻击便可获取密钥。

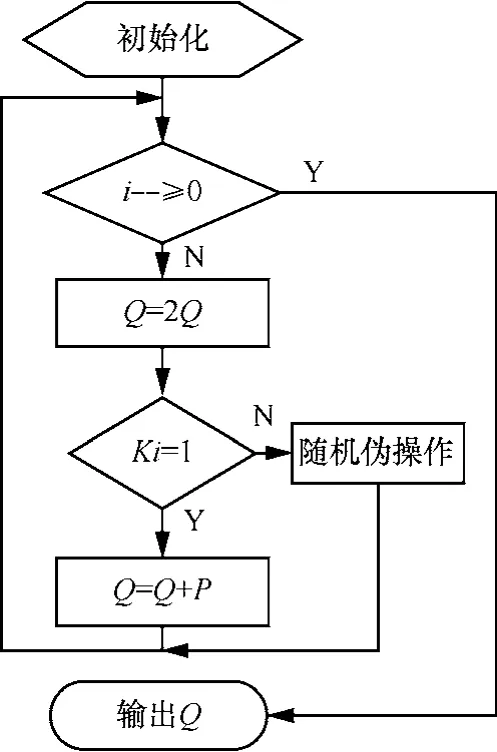
图1 随机伪操作法程序流程

3 针对随机伪操作的SPA攻击分析

3.1 单样本SPA攻击分析

根据随机伪操作算法可知，当密钥比特为0时，随机添加伪点加、伪倍点运算或无操作。当添加伪点加运算时，则该比特使真“0”变为假“1”，从波形上看无法区分；当添加伪倍点时，该比特会使单比特的“0”变为双比特的“00”；但当无操作时，真“0”将真实地表现出来。

首先，根据文献[2,8,9]以及实测数据发现，如图1所示的算法中，每个循环内部2个运算之间的时间间隔较小，而循环之间的时间间隔比较大。用时间间隔的差别，可以在单样本中定位各个不同循环轮数，这就是利用计时攻击（TA, timing attack）在单样本中获取定位信息。由于每轮循环均可被定位，而每轮循环只会对应单比特二进制数“0”或“1”。则填加的伪倍点运算会被识别出来，这是因为该运算对应的双比特“00”不可能存在于同一个轮循环中。由此可知，单样本下，每轮中观测到的“00”波形均可被还原为真实值“0”。与之相对应，固定添加伪操作算法每轮边界被区分出来也得不到对K有用的SPA攻击信息。

其次，在单样本中，还可提取密钥K汉明重量的上限。令HW（C）为二进制序列C的汉明重量（即二进制序列C中“1”的个数），K为nbit的真实密钥值，其汉明重量HW（K）为nk，Ke为单样本SPA攻击下获取K的估计值，其汉明重量HW（Ke）为ne，则有

通过计算Ke的汉明重量，可获得K的汉明重量上限。即可确定在K中最多有nk个“1”，至少存在n-ne个“0”。从暴力破解的难度上看，只需对nkbit的“1”进行真假猜测，最坏情况计算复杂度从原来的2n降到 2ne。若K为真随机数，在大数情况下，nk= [ 0.5n]的概率趋近 1，这意味着在ne中猜测有[0.5n]个“1”的猜中几率最大，即进行次猜中的几率最大。根据式（1），有

可知单样本 SPA攻击可使基于概率最大化暴力破解法的复杂度也大幅减小。由于“0”的个数下限及其位置信息的暴露，还可综合使用其他方法进行更有力、快速的密钥破解。而固定添加伪操作算法也不存在这样的缺陷。

3.2 基于SPA的多样本递推逼近攻击

由上述分析可知，想让破解复杂度降低，在n不变的情况下，应尽量使ne的值接近nk。进行SPA攻击时，可先进行L个样本获取，然后对每个样本进行SPA攻击，获取不同Kei(1≤i≤L)，选取其中汉明重量最小的猜测值Kej(1≤j≤L)，再进行其他类型攻击。事实上，在多样本条件下，还存在更有效的分析攻击方法。

3.2.1 随机伪操作的分析模型

从密码分析和波形分析的角度看，随机伪操作法可看作将K中的“0”进行掩码保护，随机编码成“0”、 “00”或“1”，而对K中的“1”并未进行掩码，仅编码成“1”。由于单样本 TA攻击在可直接将“00”反推成“0”，故“00”这种情况在下面的分析中将归结于“0”中而不单独讨论。

根据这种规则，可得如下密码分析模型：

其中，K为nbit的真实密钥，R为nbit的真随机数，Ke为单样本SPA攻击后猜测值，运算符“+”为按比特做逻辑“或”运算。易验证该模型完全符合以上编码规则。

3.2.2 多样本递推逼近SPA攻击的原理

在多样本条件下，令L为采集的样本次数，则第i个样本利用真随机数Ri形成的猜测值Kei为

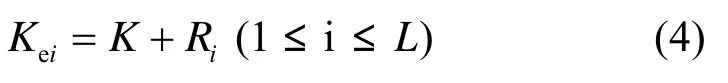
其中， 当i≠j时 ,Ri≠Rj。

令KL'为多样本综合猜测值，构造以下运算：

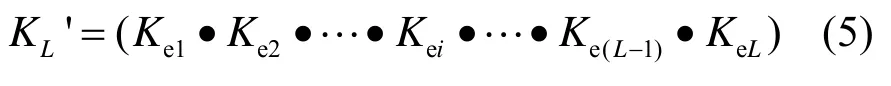
其中，运算符“·”为按比特做逻辑“与”运算。

将式（4）代入式（5），根据逻辑运算规则，有：

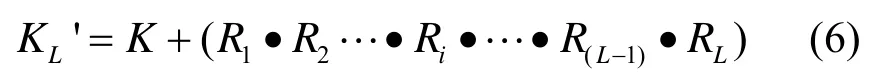
从密码破译的角度看，KL'和真实值K两者的差值正是随机数RL'，该随机数中“1”的个数越少，则猜测值越接近于真实值。

根据随机数性质，当L充分大的时候，有

则当L充分大时：

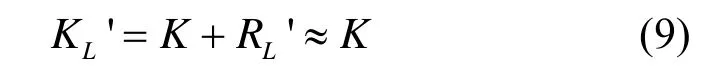
另外，当在原样本集合中再增加一条新样本时，有

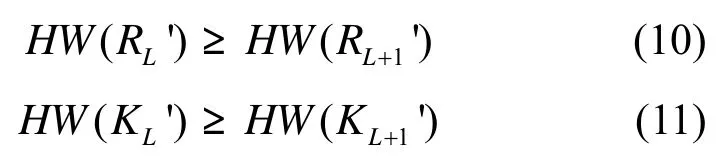
这说明每增加一条新样本，KL+1'将越接近于真实值K。

3.2.3 多样本递推逼近SPA攻击的实现算法

根据以上性质，构造新型多样本攻击算法如下。

算法1多样本递推逼近S PA攻击算法

输入：C=[K]P

输出：Ki' =K

1) 初 始化：K0'为全1的比特序列，i=0

2)i=i+ 1， 单样本S PA攻击出猜测值Kei

5)若Ci≠C，则转至2）继续

6)返 回Ki'

在真随机数条件下，根据其均匀性有

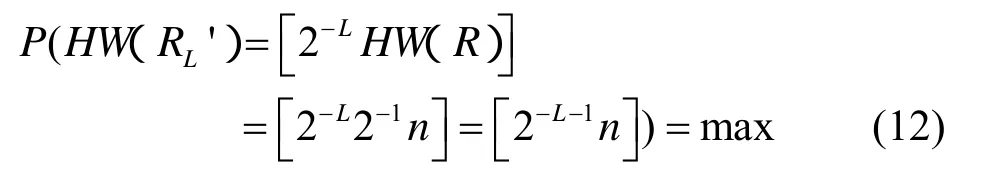
根据上面的讨论可知，L个样本猜测后得到的猜测值K'正确猜出密钥的概率最高，当L= l bn-1时，有

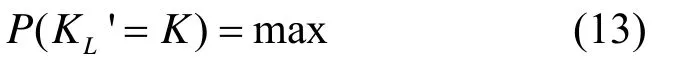
由信息熵理论也可得到类似的结果。

如此可见，攻击样本数L与受攻击K的比特数n之间呈对数关系，计算复杂度极小，攻击效率比一般的多样本攻击高得多。例如一个n=256的K在7个样本下就有极高的几率被完全攻破。

3.2.4 多样本递推逼近攻击实测实验结果分析

实验1 在n=256bit时，对一个汉明重量为130的密钥K，实施多样本递推逼近攻击，共独立测试10 000组，每组均用不同的随机数进行伪随机操作。测试结果频数直方图如图2所示，7个样本攻击成功的频数最高，为2 401次，占总次数的24.01%。其次是6个样本攻击成功，频数为2 336次，占总次数23.36%。攻击成功所花样本数 11L≤ 的百分比为97.03%， 13L≤ 的百分比是99.25%

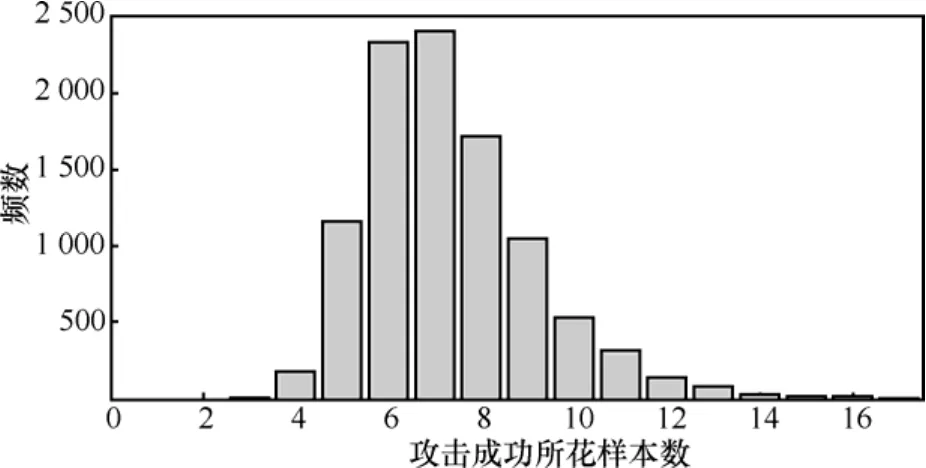
图2n=256bit密钥K的10 000组攻击成功样本数频数直方图

实验2 对n=1 024bit，汉明重量为541的密钥K，对其实施多样本递推逼近攻击。10 000组测试后，测试结果频数直方图如图3所示。

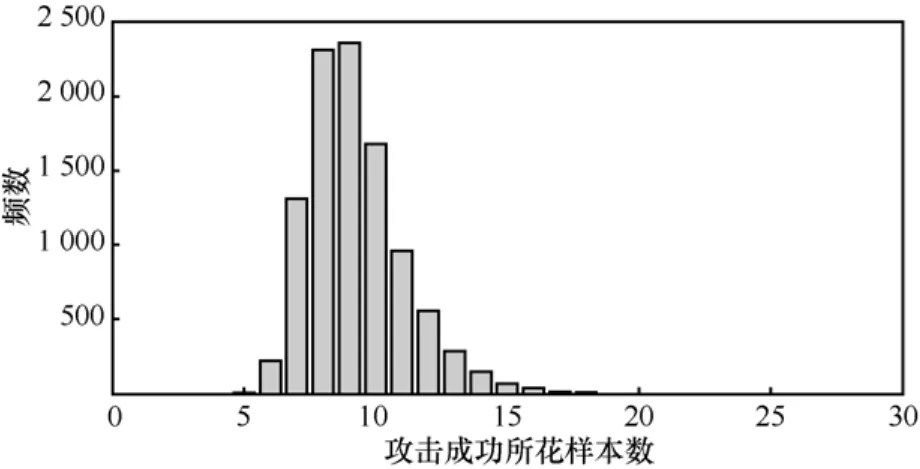
图3n=1 024bit密钥K的10 000组攻击成功样本数频数直方图

由图3可知，当成功攻击样本L=9时的频数最高，为2362次，占23.62%；其次为L=8，为2 313次，占 23.13%，攻击成功所花样本数L≤ 1 3的百分比为97.09%,L≤ 1 5的百分比是99.28%。

经过大量实验统计分析得到，对于nbit的密钥K，成功攻击所花样本数L≤lbn+3的概率大于97%，L≤lbn+5的概率大于99%。这说明只需小于等于lbn+3个样本，就有97%的概率破解出完整的nbit密钥，在此基础上再增加2个样本则有大于99%的概率成功破解。

4 随机伪操作算法抗 SPA攻击可能的改进措施

随机伪操作算法中存在的多样本递推逼近攻击缺陷主要由以下原因造成。

1) 由于轮与轮之间的时间间隔与循环体内的时间间隔不同，可获得定位信息。

2) 由于运算的不同，倍点和点加运算在功耗曲线上很容易被辨识出来。结合随机伪操作算法，可获得每轮K的信息。

3) 掩码采用真随机数，对于相同的K每次都用不同的随机数进行掩码，而多样本递推逼近攻击正是针对这种随机机制实施的攻击。

针对第1个缺陷，需在精确测量的基础上，加入适当的延时机制，使得各运算之间的时间间隔相等，消除TA攻击的隐患。

针对第2种缺陷，需要在倍点和点加运算算法中加以改进，使得2种运算的操作相等，这样在功耗曲线上无法区分2种不同运算，给SPA攻击识别“0”、“1”增加难度。

针对第3种缺陷，则需规定随机数生成算法的规则，对相同的K生成相同的随机数R，不同的K生成不同的随机数R。固定添加伪点加算法是该改进的一个特例，其添加的随机数R为K的反码，这样可使得任意K对应的Ke均为固定值：全“1”。值得指出的是，该随机数产生算法最好能保证其单向性，即使在获得随机数R信息的条件下，仍无法逆推出K的值。其实现方案可使用散列技术或将K作为随机数发生器的种子，其破解的复杂度就等价于破解散列算法或随机数发生器。

特别要指出的是，修正以后的算法，其安全性仍然低于固定添加伪点加算法。首先，攻击者仍可获得K序列汉明重量的上限，其次，虽然不能确定“0”的绝对位置，但可确定“0”和“1”的相对前后位置，最后，还可通过观察“0”和“1”的行程来确定子序列中“0”的最少个数和“1”的最多个数，这些信息均可使攻击难度大大下降，由此可见，消除倍点和点加运算之间的差别也非常重要，具体攻击过程另文撰述。

5 结束语

随机伪操作椭圆曲线标量乘算法虽然将运算效率提高，但本文证明，其抗 SPA攻击能力大大降低。本文提出的多样本递推逼近攻击，利用在多样本中消除随机数的方法，实测结果表明只需小于等于lbn+3个样本，就有97%的概率破解出完整密钥。该类攻击的存在证明，不恰当的应用随机性，不但不能增加安全性，反而会产生极大的安全缺陷。

在改进措施中，将随机数生成算法进行改进，有效抵抗了多样本递推逼近攻击；同时平衡了运算之间的时间间隔。但必须认识到，由于随机添加伪操作算法本身的缺陷，其安全性仍弱于固定添加伪点加算法，建议不使用该类算法。

[1] KOCHER P, JAFFE J, JUN B. Differential power analysis[A]. Lecture Notes in Computer Science; Proceedings of the 19th Annual International Cryptology. Conference on Advances in Cryptology[C]. 1999.388- 397.

[2] KOCHER P C. Timing attacks on implementations of Diffie-Hellman,RSA, DSS, and other systems[A]. Advances in Cryptology-CRYPTO'96, of Lecture Notes in Computer Science[C]. 1996.104-113.

[3] 朱冰, 陈运, 吴震等. 一种抗简单功耗分析攻击的椭圆曲线标量乘快速实现算法[J]. 成都信息工程学院学报. 2011, 28(1):5-10.ZHU B, CHEN Y, WU Z,et al. A fast algorithm of scalar multiplication on ECC resistant against SPA[J]. Journal of Chengdu University of Information Technology, 2011, 28(1):5-10.

[4] 廖嘉, 夏国坤, 王立鹏等. 抵抗SPA和 DPA的椭圆曲线上点的标量乘法[J]. 天津科技大学学报, 2009, 24(2):67-70.LIAO J, XIA G K, WANG L P,et al. Scalar multiplication on ECC resistant against SPA and DPA[J]. Journal of Tianjin University of Science and Technology,2009,24(2): 67-70

[5] TETSUYA I, BODO M, TSUYOSH T. Improved elliptic curve multiplication methods resistant against side channel attacks[A].Progress in Cryptology, LNCS 2551[C]. Springer-Verlag, 2002.295-313.

[6] MILLER V S. Use of elliptic curves in cryptography[A]. Proceedings of Crypto 85 LNCS 218[C]. Springer, 1986. 417-426.

[7] KOBLITZ N. Elliptic curve cryptosystems[J]. Mathematics of Computation, 1987,(48):203- 209.

[8] ACICMEZ O, SEIFERT J P, KOC C K. Predicting secret keys via branch prediction[A]. Topics in Cryptology-CT-RSA 2007, Leture Notes in Computer Science[C]. 2006.225-242.

[9] ACIICMEZ O, KOC C K, SEIFERT J P. On the Power of Simple Branch Prediction Analysis[R]. Cryptology ePrint Archive, 2006.312-320.