基于AF协作的多中继M2M通信系统的SER性能分析

张南，宫丰奎，葛建华

（西安电子科技大学 ISN国家重点实验室，陕西 西安 710071）

1 引言

随着无线通信越来越广泛的应用，移动终端对移动终端(M2M, mobile-to-mobile)通信场景引起了更多的关注，例如机车间通信、移动ad hoc网、军事通信等。不同于传统的固定终端对固定终端(F2F,fixed-to-fixed)或固定终端对移动终端(F2M,fixed-to-mobile)通信，M2M通信场景中的收发机都处于移动状态，从而收发机之间构成双移动通信信道，而且，由于移动终端配置的通常都是低仰角天线，传统的F2F和F2M场景下的瑞利衰落等信道衰落模型已不适用。目前，研究如何对M2M信道建模已经是一个热点问题，成果表明[1～3]：M2M信道经历的衰落更为严重，其中，N×Nakagami-m分布[1]可以很好地表征典型的M2M信道衰落分布。

在克服信道衰落的方案中，实现复杂度较低的放大转发(AF, amplify-and-forward)中继辅助通信是传统通信场景下一种比较有效的方案。目前，相关的性能研究取得了众多成果，如文献[4]和文献[5]分析了采用最大比合并时AF系统在瑞利和Nakagami衰落信道下的平均误符号率(SER, symbol error rate)和中断概率。但是，目前很少有论文涉及协作M2M系统的性能分析问题。文献[6]利用信道自相关函数特性提出了针对移动中继场景的信道估计算法，但没有分析中继移动时的系统性能。基于重叠Nakagami-m信道，宫丰奎等[7]推导了基于译码转发(DF, decode-andforward)协议的单中继M2M系统的精确SER和渐进SER表达式。文献[8] 基于该类信道研究了AF中继模型下系统的成对错误概率，但文献[8]仅考虑了单中继场景。本文正是考虑到文献[8]的研究局限性，针对更一般化的多 AF中继场景，从矩母函数(MGF,moment generating function)分析的角度，推导了系统SER性能下界表达式和近似SER表达式。

2 MAF-M2M系统和信道模型

2.1 MAF-M2M系统模型

MAF-M2M通信系统如图1所示。系统中包含一个移动源节点(MS)、一个移动目的节点(MD)以及N个移动中继节点(MR)。hSD、hSRk、hRDk(k= 1,…,N)分别表示链路MS-MD、MS-MRk以及MRk-MD的复信道衰落系数。假定节点以半双工模式工作，配置单发单收天线。第1个时隙(S1)，MS以功率PS向所有MR以及MD发送信息x，第2个时隙(S2)到第N+1个时隙(SN+1)，中继节点 MR1，MR2，…，MRN分别将接收到的信号以功率Pk发送到MD。最后，MD将N+1个时隙接收到的信号进行合并，从而获得空间分集增益。为了获取最大的合并增益，本文考虑最大比合并(MRC, maximum ratio combining)算法[9]。

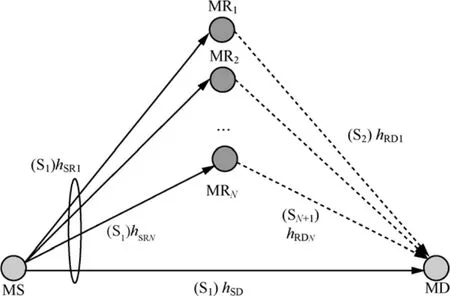
图1 MAF-M2M通信系统模型

2.2 重叠Nakagami-m信道模型

第一时隙，源节点以功率PS向MD以及所有MR发送信息x，目的端MD与中继MRk接收到的信号rSD、rSRk分别表示为

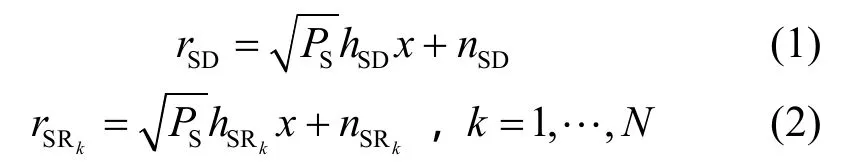
设复信号x平均功率为1，第k个中继MRk的放大增益是kα，则第k+1个时隙MD接收到的信号可以表示为[6]

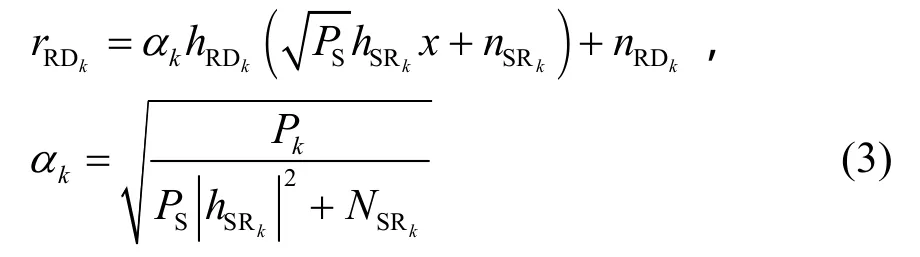
式(1)～式(3)中,nSD、nSRk、nRDk均为零均值高斯白噪声，方差分别为NSD、NSRk以及NRDk。信道衰落系数hSD、hSRk、hRDk服从独立但不同分布的重叠Nakagami-m分布。

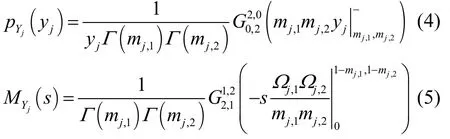
其中，Г(·) 为 Gamma 函数,G(·) 为 Meijer-G函数[11]，且表示数学期望。

2.3 接收合并信号及接收信噪比表示

MD采用性能最优的MRC合并算法时[9], 接收信号可以表示为

将式(1)、式(3)代入式(6)可得：

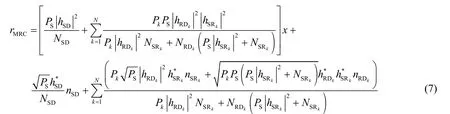
由式(7)，假定目的端已知准确的信道状态信息(CSI, channel state information)hSD、hSRk和hRDk，则输出信噪比(SNR)可以计算为

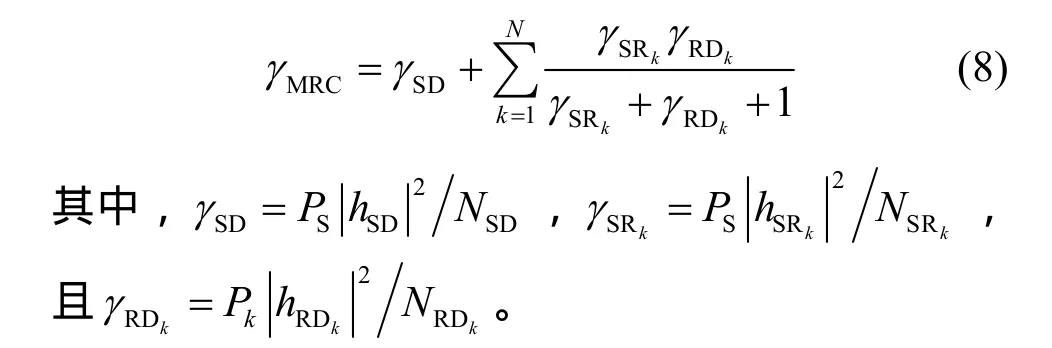
3 MRC合并下的SER性能分析

由于对M-PSK调制信号而言，任意信噪比γ下的条件SER为[4]

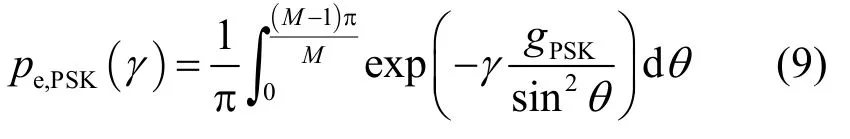
这样，假定MD端已知准确的CSI信息hSD、hSRk和hRDk，采用相干检测，基于信道衰落系数的条件SER可以表示为pe（hSD,hSRk,hRDk）

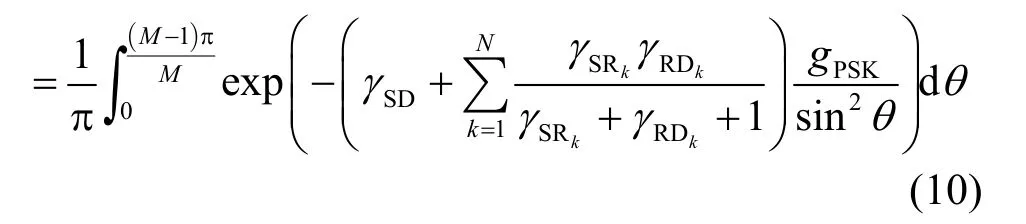
对各个信道衰落系数求期望，可以得到平均SER

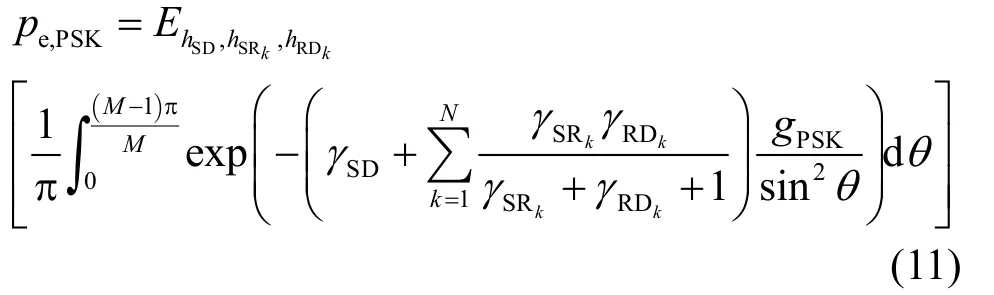
直接求解式(11)是一个非常复杂的数学问题。据查，目前已有成果基本都基于Rayleigh或者Gamma分布的假设[12]，在重叠Nakagami-m分布下还没有很好的解决方法，因此，本文转而利用算术—几何不等式[13]来求解 SER的宽松下界，并利用概率密度函数(PDF)近似的方法得出其较为精确的近似表达式。

3.1 基于算术—几何不等式的SER下界

为了得到式(11)中求和各部分对应变量的MGF，考虑到

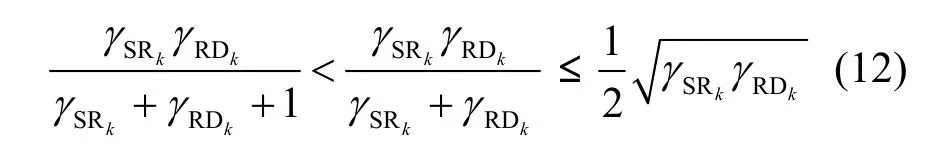
式(11)可以进一步化简为

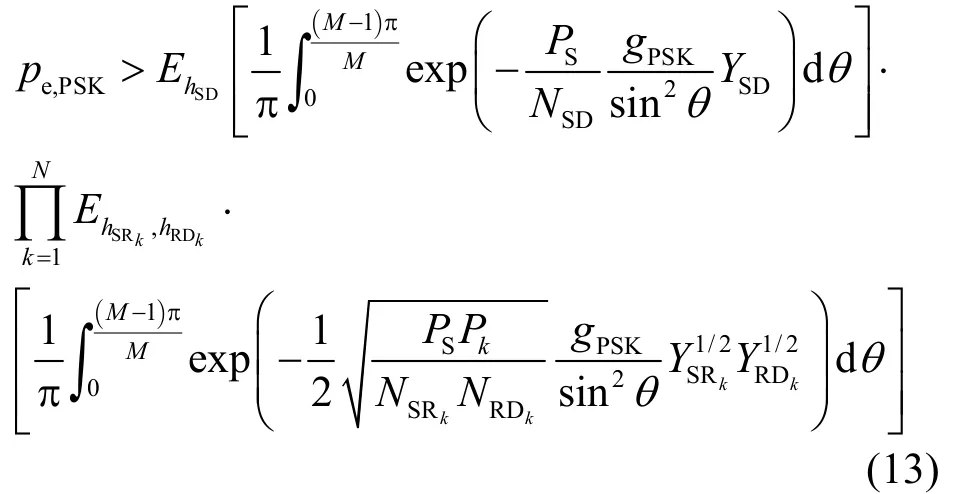
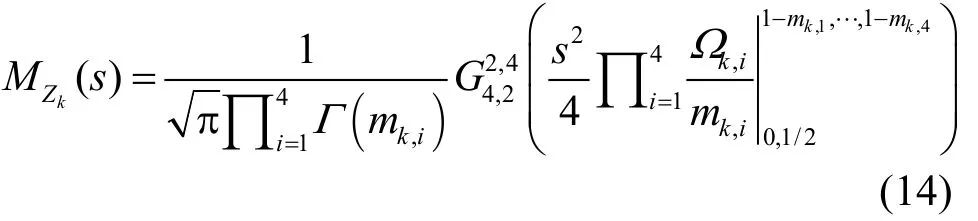
结合式(5)，交换式(13)中求期望和求积分的次序，于是得到：

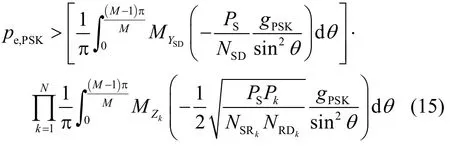
上述 SER的下界表达式含有单积分。由于Meijer-G函数在MAPLE等数学计算软件中为标准函数，因此式(16)可以通过软件求数学积分得值。

3.2 基于近似PDF的SER计算

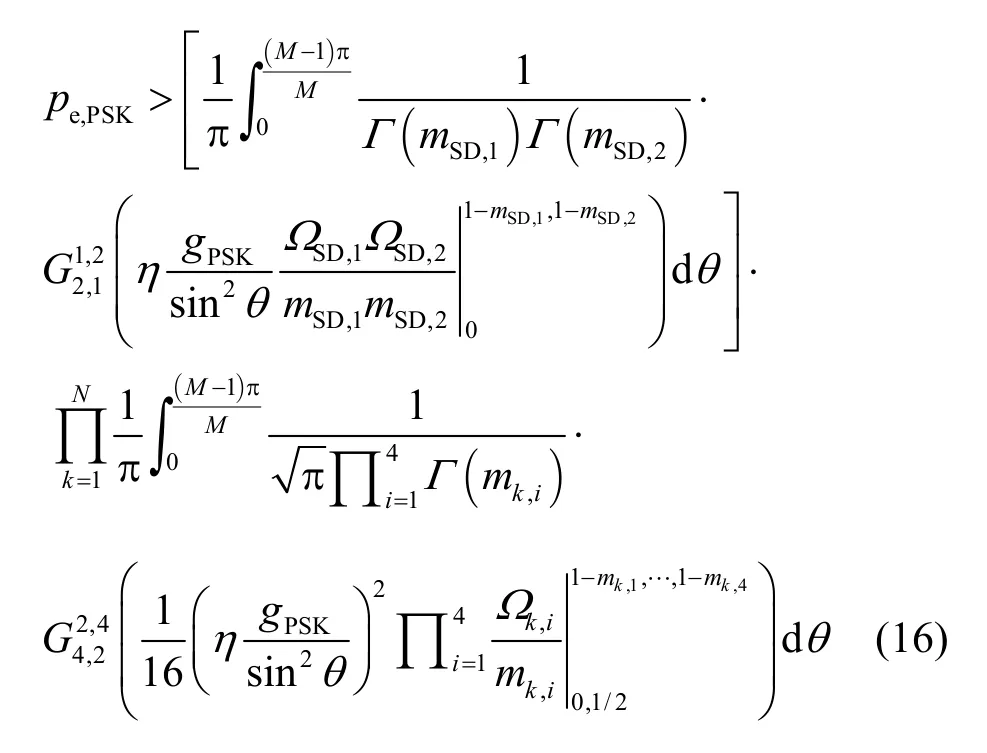
注意到，式(16)的推导过程中利用了算术—几何不等式，导致理论结果和实际结果可能差距较大，特别是当参数m取值较小时。为了得到更为精确的SER表达式，考虑等功率分配以及独立同分布场景，且mk,1=mk,2=m，此时部分转化为式(17)，定义为YHM。

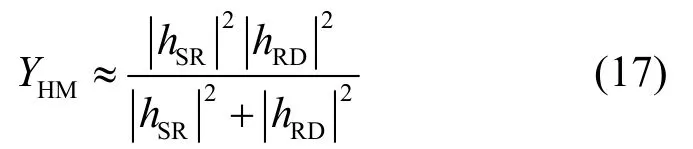
由于直接求解YHM的准确 PDF表达式非常困难，类似文献[14]以及文献[15]，转而通过统计方法求其近似PDF。统计研究结果表明：YHM的PDF和Gamma分布[11]匹配较好，如图 2所示。因此，采用Gamma分布代替YHM的精确PDF。通过利用一些数学软件中的通用函数，很容易得到Gamma 分布的最佳参数(a和b), 如MATLAB中的gamfit函数。 例如，对应m=0.5计算得到的最佳参数a和b分别为0.287 8 和 0.474 8，如图2所示。这样，式(16)成为

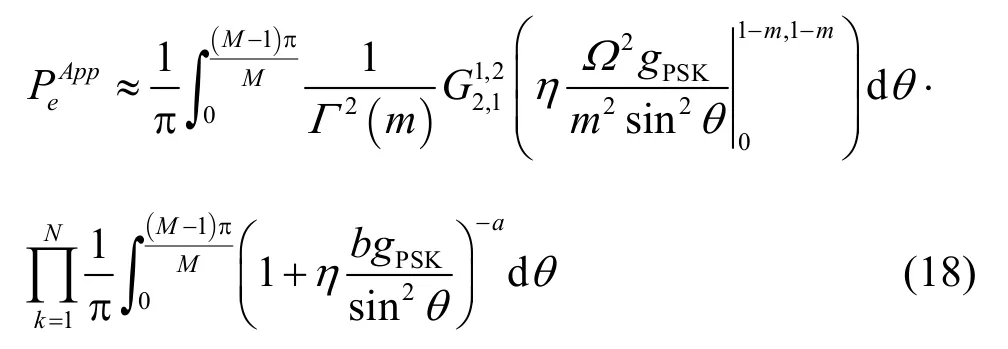
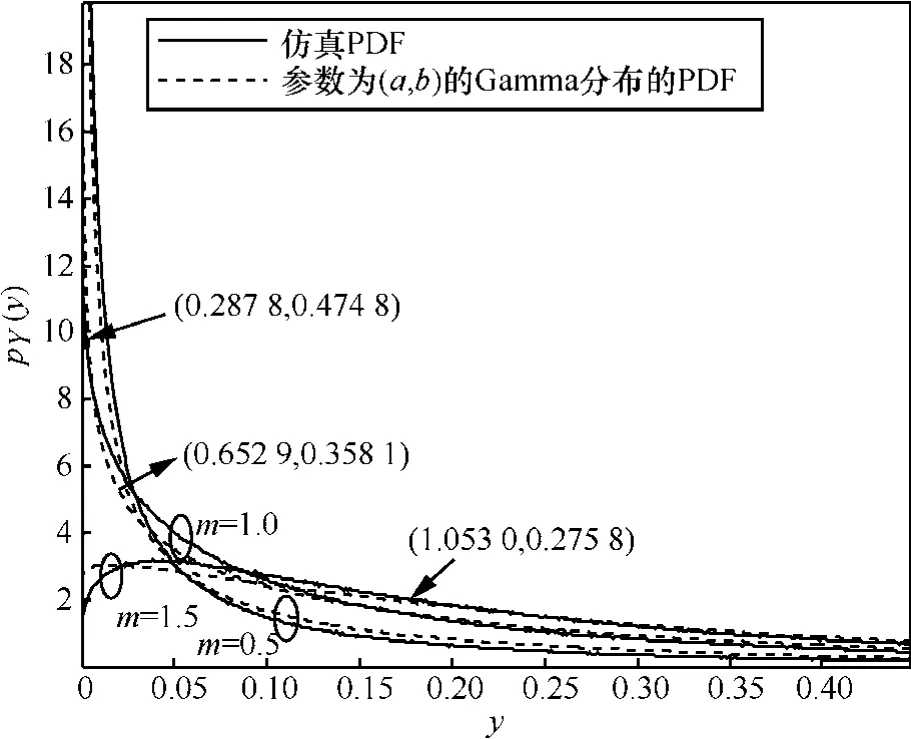
图2 仿真PDF和标准Gamma分布的比较(最佳参数由MATLAB中gamfit函数得到)

4 计算机仿真

本节通过计算机仿真证明前文推导理论结果的准确性。仿真条件：假定mSD,1=mSD,2=mk,i=m，ΩSD,1=ΩSD,2=Ωk,i= 1 ，i= 1 ,2,3,4，不失一般性，同时假定NSD=NSRk=NRDk=N0，PS=Pk=P，并定义SNR≜η=P/N。其中，本节蒙特卡罗仿真中每信噪比点的SER结果是在迭代1 000次，每次106个调制符号的条件下得出。

图3给出了m取值为1时，不同中继数配置条件下(中继数N为1～4)，基于4-PSK调制的AF协作系统在典型重叠 Nakagami-m信道[6]下的SER性能曲线比较，其中虚线表示的理论性能下界根据式(16)得到，此时M=4，gPSK= 1/2。图4给出了中继数N为1，m分别取值为2, 4, 8时，基于 4-PSK调制的 AF协作系统在典型重叠Nakagami-m信道下的SER性能曲线。由图3和图4可知，目的端采用MRC合并时，AF中继可以明显改善不同m参数下M2M通信系统性能，说明MAF-M2M方案不失为一种提高M2M通信可靠性的有效手段。图3和图4还表明：当m较小时, 理论下界和仿真曲线差距较大，如考虑单中继且m=1，当SER=10-4时，两者之间的差距接近5dB；随着m增大，理论下界越接近仿真性能，如图4所示，m增至8时，差距小于1dB。这个差距是因为：式(15)及式(16)的推导过程中利用了式(12)所示的算术—几何平均不等式，该不等式在2个变量相等时等号成立，反之，若两变量差距较大，不等式两边差距也较大。m等于1时，信道等效为层叠Rayleigh衰落信道，信道衰落变化较剧烈，从而导致不等式两边差距较大，体现在理论界和实际仿真曲线间的误差较大；m越大，衰落幅度起伏越平缓，不等式差距减小，相应SER曲线间的误差减小。由图3和图4还可以近似得出理论下界和仿真结果曲线近似平行，该结论可以应用到下一步的分集度分析等方面。

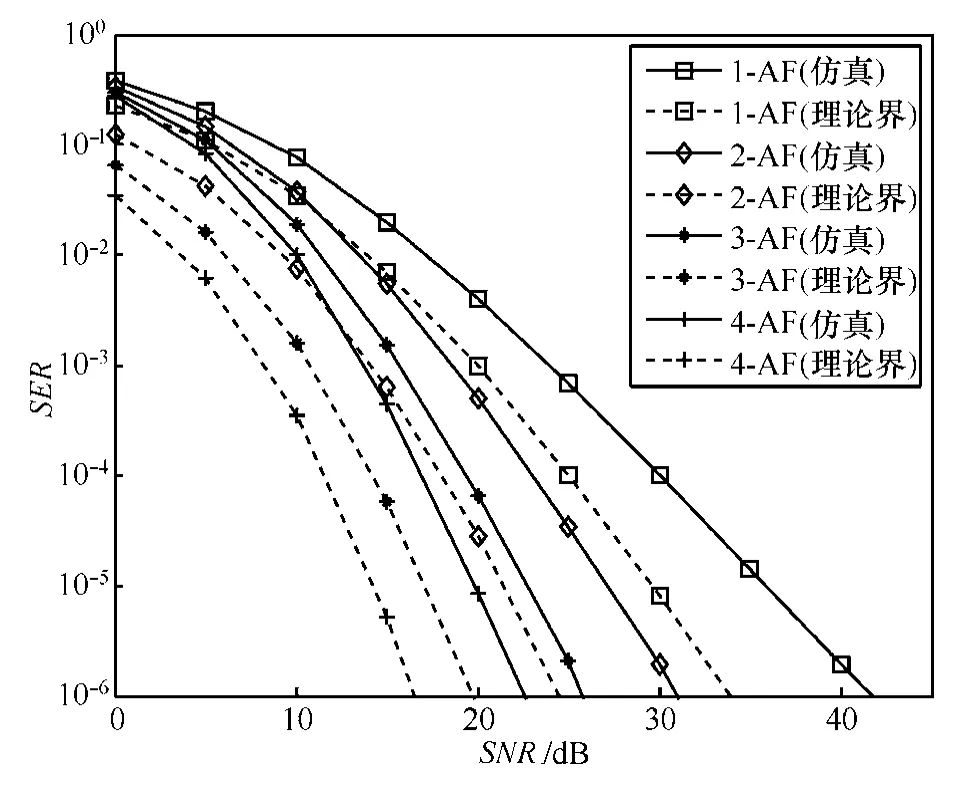
图3 4-PSK，m=1时MAF-M2M系统SER仿真和理论界比较（中继数1～4）

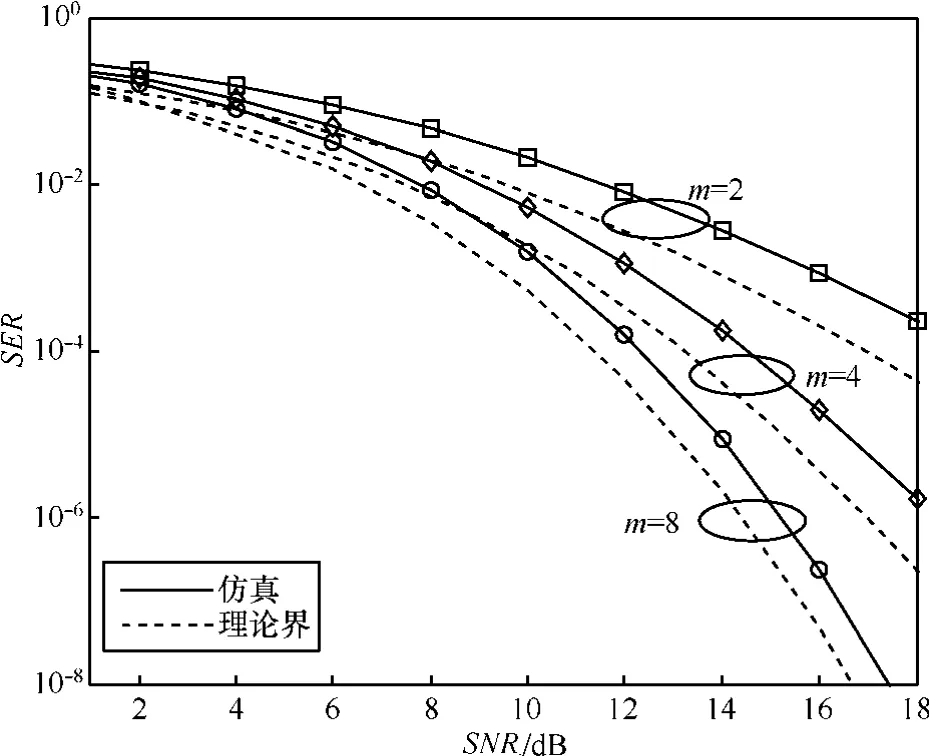
图4 4-PSK，m=2, 4, 8时MAF-M2M系统SER仿真和理论界比较（中继数为1）

图5进一步给出了单中继条件下近似SER和SER下界性能以及仿真结果的比较, 其中，m选择为0.5, 1.0, 1.5。如图5所示, 相较SER下界，近似PDF方法得到的 SER性能曲线和仿真结果在中高信噪比区间匹配较好，和m取值无关，低信噪比时的性能差异是由于式(17)分母中省略了式(12)中的常数项1导致的。

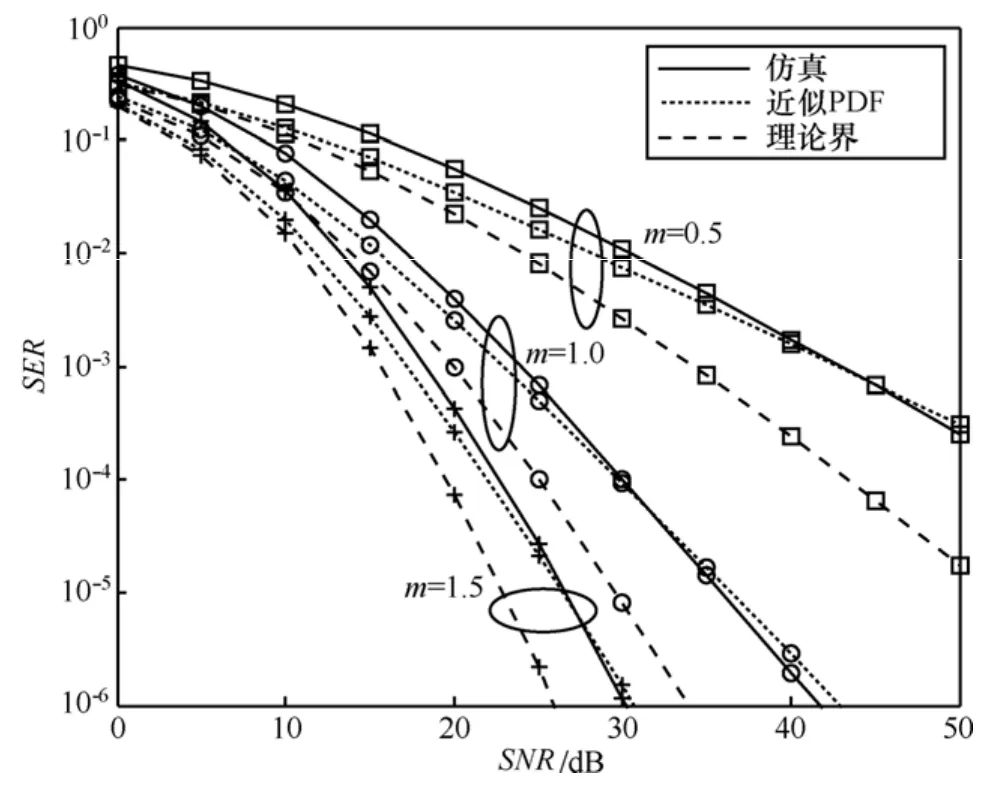
图5 4-PSK调制，单AF中继场景下近似PDF方法和SER下界以及仿真结果的比较

5 结束语

通过理论界推导、近似SER计算和计算机仿真联合说明MAF-M2M系统方案在重叠Nakagami-m衰落信道下的性能，结果表明了协作 AF方案在M2M信道中应用的有效性。基于MGF函数的SER公式推导方法的关键在于：接收等效信噪比计算和其MGF推导，本文通过计算SER下界避免了过于繁琐的数学处理。仿真结果同时表明了近似PDF方法的紧致性。

[1] KARAGIANNIDIS G K, SAGIAS N C, MATHIOPOULOS P T.N*Nakagami: a novel stochastic model for cascaded fading channels[J].IEEE Trans on Commun, 2007, 55(8):1453-1458.

[2] PATEL C S, STÜBER G L, PRATT T G. Simulation of Rayleigh-faded mobile-to-mobile communication channels[J]. IEEE Trans on Commun, 2005, 53(11):1876-1884.

[3] ZAJI´C A G, STÜBER G L. Three-dimensional modeling and simulation of wideband MIMO mobile-to-mobile channels[J]. IEEE Trans on Wireless Commun, 2009, 8(3):1260-1275.

[4] RIBEIRO A, CAI X, GIANNAKIS G B. Symbol error probabilities for general cooperative links[J]. IEEE Transactions on Wireless Communications, 2005, 4(3):1264-1273.

[5] IKKI S, AHMED M H. Performance analysis of cooperative diversity wireless networks over Nakagami-mfading channel[J]. IEEE Communications Letters, 2007, 11(4):334-336.

[6] PATEL C S, STÜBER G L. Channel estimation for amplify and forward relay based cooperation diversity systems[J]. IEEE Trans onWireless Commun, 2007, 6(6):2348-2356.

[7] GONG F K, GE J H, ZHANG N. SER analysis of the mobile-relay-based M2M communication over double Nakagami-mfading channels [J]. IEEE Commun Letters, 2011, 15(1): 34-36.

[8] İLHAN H, UYSAL M, ALTUNBAŞ İ. Cooperative diversity for intervehicular communication performance analysis and optimization[J]. IEEE Trans on Veh Technol, 2009, 58(7):3301-3310.

[9] BRENNAN D G. Linear diversity combining techniques [J]. Proceedings of the IEEE, 2003, 91(2):331-356.

[10] KARAGIANNIDIS G K, TSIFTSIS T A, MALLIK R K. Bound for multihop relayed communications in Nakagami-mfading[J]. IEEE Trans on Communications, 2006, 54(1):18-22.

[11] GRADSHTEYN I S, RYZHIK I M. Table of Integrals, Series, and Products[M]. New York: Academic, 2007.

[12] HASNA M O, ALOUINI M S. Harmonic mean and end-to-end performance of transmission systems with relays[J]. IEEE Trans on Commun, 2004, 52(1):130-133.

[13] CHEN X, ZHOU Q F, SIU T W,et al. Asymptotic analysis of opportunistic relaying based on the max-generalized-mean selection criterion[J]. IEEE Trans on Wireless Communications, 2011, 10(4):1050-1057.

[14] SEDDIK K G, SADEK A K, SU W,et al. Outage analysis of multi-node amplify-and-forward relay networks[A]. IEEE Wireless Communications & Networking Conference,WCNC2006[C]. Las Vegas, NV USA, 2006.1184-1188.

[15] Al-AHMADI S, YANIKOMEROGLU H. On the approximation of the generalized-KPDF by a Gamma PDF using the moment matching method [A]. IEEE Wireless Communications & Networking Conference, WCNC2009[C]. Budapest, Hungary, 2009.1-6.

[16] BEAULIEU N C, CHENG C. Efficient Nakagami-mfading channel simulation[J]. IEEE Trans on Veh Technol, 2005, 54(2):413-424.