基于协作认知网络的虚拟MIMO信号及干扰分布特性研究
2012-08-04鲍煦宋铁成沈连丰
鲍煦,宋铁成,沈连丰
(1.江苏大学 计算机科学与通信工程学院,江苏 镇江 212013;2.东南大学 移动通信国家重点实验室,江苏 南京 210096)
1 引言
虚拟MIMO技术继承了MIMO技术的优点并且更适合在分布式无线网络中应用(每个节点只配有单天线),因此近来越来越受到研究者的关注[1~3]。为了度量虚拟MIMO技术给网络传输容量带来的提升,文献[4]引入了节点传输成功概率的概念。此成功概率的计算需要通过推导信号和干扰的互补累积分布函数 (CCDF, complimentary cumulative distribution function)来实现[5]。然而,由于无线网络中节点空间位置的随机性使得信号和干扰的CCDF分布很难求得。文献[6]推导了干扰的CCDF上下界,但其上界并不紧致,与仿真的实际结果有较大的差异。此外,关于虚拟MIMO信号的分布特性在最近的文献中都没有提及。本文提出一种应用于认知网络的虚拟 MIMO传输方案,推导虚拟MIMO信号和干扰的CCDF分布函数的上下界及其渐进特性。
2 系统模型及传输方案
2.1 系统模型
系统模型如图1所示,主从用户共同存在同一区域,从用户与主用户共用频谱资源。主从用户节点构成分布式ad hoc网络,其发送端节点在空间中的坐标位置建模为均匀泊松点过程(HPPP, homogeneous poisson point process)Φ={x1,x2,…}⊂ℝ2。从用户发送端与接收端的距离假设是固定的,并且接收端的空间坐标并不在泊松点过程Φ内。将主用户发送端的位置设置为坐标原点,主用户接收端位于坐标z= (0,z)。在该系统中,主用户已知从用户节点的存在并能相互协作。从用户发送端以概率p发送数据,概率=1-p侦听主用户的活动。该系统中所有的节点假设同步,从用户之间的同步可以通过侦听主用户收发双方传输数据的同步前缀来实现。假设主用户发射功率为Pp,从用户发射功率为Ps。信道衰落假设在空间和时间上相互独立,并且具有单位方差。任意节点位置x和y之间的信道衰落功率函数定义为hxy,大尺度路径损耗函数定义为,其中,α是路径损耗因子,满足α>2。因此主用户接收端所受到的系统干扰为
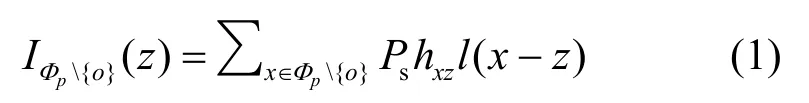
其中,Φp表示主从用户发送节点的集合(以概率p发送数据),Φp表示静默从用户集合(即以概率=1-p静默)。由于主用户发送端在集合Φp内且位于原点o,因此主用户接收端的干扰来自集合Φp {o}内。当从用户空间密度较大时,用户之间的干扰远远大于背景噪声,所以本文不考虑噪声对系统的影响。

图1 系统模型
2.2 传输方案
主用户与从用户工作在同一频段,为了提高主用户传输数据的抗干扰能力,主用户为邻近的静默从用户分配若干时隙以便静默从用户为其转发数据。具体方案如图2所示。
1) 主用户首先向周围的从用户发送“询问”数据分组。该数据分组类似于训练序列,一方面可供静默从用户测试信道信干比(SIR, signal interference ratio),另一方面“询问”数据分组也包含主用户的身份号,以区分不同的主用户。
2) 邻近的静默从用户接收到“询问”数据分组后,立即测量SIR值,若其SIR满足式(2),则向主用户发送“应答”数据分组通知主用户其符合协作
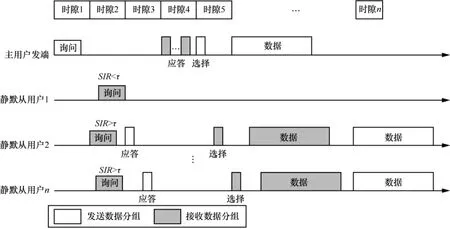
图2 虚拟MIMO传输方案举例
条件,主用户则发送“选择”数据分组通知被选从用户准备组成虚拟MIMO阵列为其转发数据。
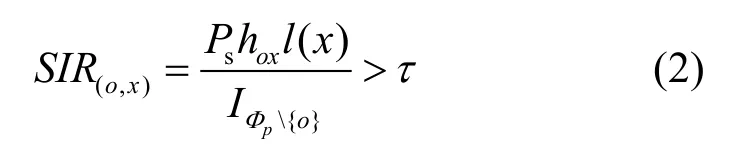
其中,τ是SIR阈值,IΦp{o}表示静默从用户在位置x处所受到的干扰:
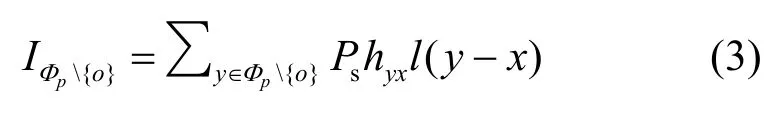
3) 当主用户完成数据传输后,虚拟MIMO阵列中的从用户利用主用户为其分配的时隙同时译码转发(decode and forward)至主用户接收端,完成协作传输。
基于以上传输方案,在主用户接收端的信号可以表示为
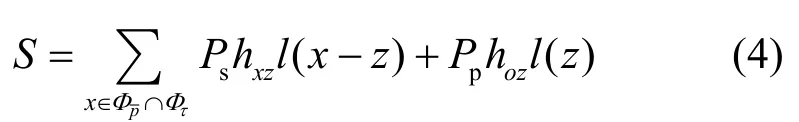
其中,
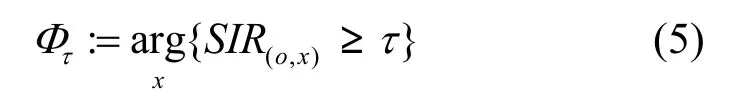
通常ad hoc网络干扰信号是空间相关的,因此式(4)中虚拟MIMO信号同样空间相关,所以Φτ不是泊松点过程。然而当信道路径衰落模型为l(x)=| |x||-α时空间相关性趋于 0[5],因此本文中随机点过程Φτ可以视作泊松点过程。
3 虚拟MIMO信号和干扰的CCDF上下界及其渐进分布
本节分析协作认知网络中虚拟 MIMO信号和系统干扰的CCDF上下界,并给出渐进分布。分析的结果具有普适性,并不拘泥于第2节提出的虚拟MIMO传输方案。
定义E!o(·)为去心 Palm测度(reduced palm measure)的数学期望[7],它是点过程的条件期望函数(即给定点过程中某个点在坐标原点,但不包括该点的期望)。用点来表示条件生成函数G作用的变量,例如下文的分析将用到随机几何知识,特别是泊松点过程的概率生成函数(PGFL, probability generating functional)和Palm分布以及Campbell-Mecke定理[7]。
定理 1 当从用户发送节点为空间密度是λ的均匀泊松点过程时,假设节点发送数据概率为p,条件生成函数为G,虚拟MIMO信号的互补累积分布函数:的下界是上界是
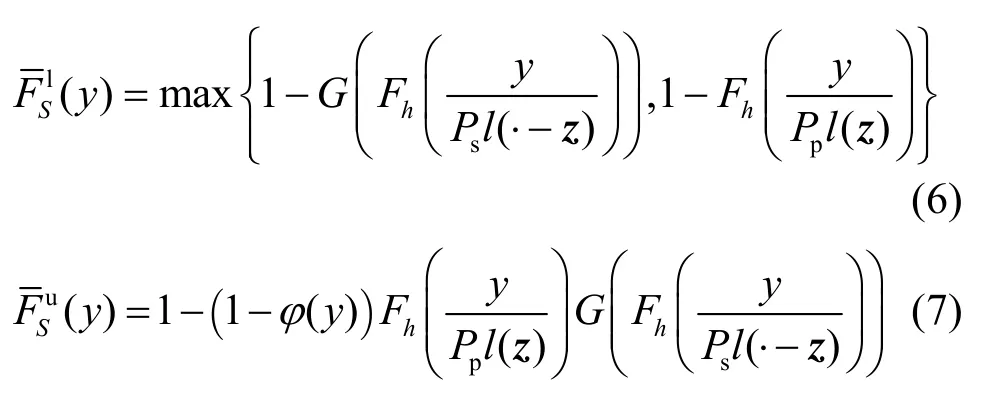
其中,Fh(·)为信道功率衰落的累积分布函数(CDF,cumulative density function)。
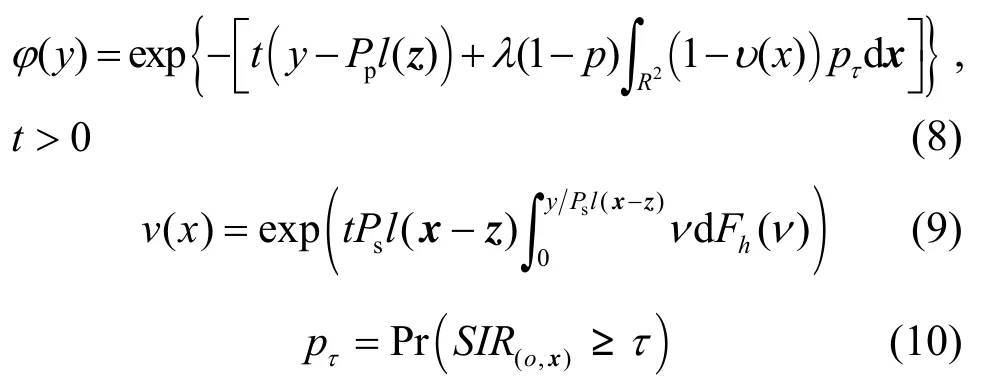
证明 由于Φτ和都是泊松点过程,根据泊松点过程的定义[7],集合∩Φτ仍然是泊松点过程,将其分为2个子集:
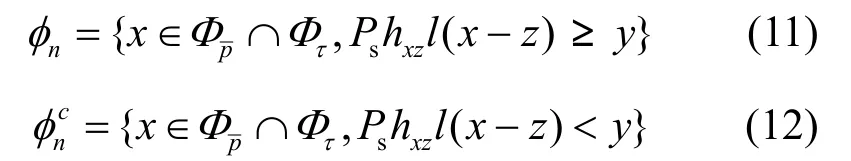
所以虚拟MIMO信号的CCDF函数为
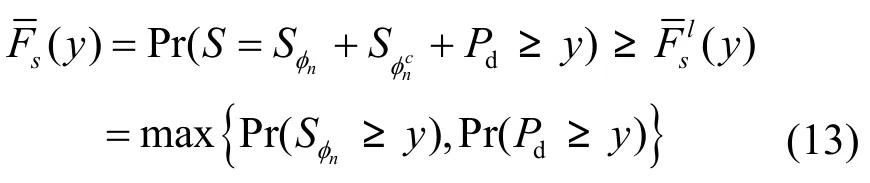
其中,dP为在主用户接收端的直接传输功率:
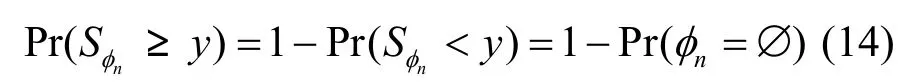
集合nφ为空集的概率可以用去心条件期望函数(reduced conditional expectation function)得到:
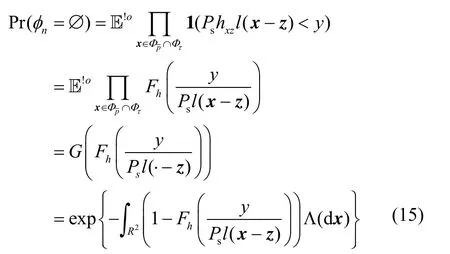
上式中最后一行根据泊松点过程的概率生成函数定义可得。
Λ(·)定义为∩Φτ集合中的二维随机测度,这是非均匀泊松点过程。因为在集合Φτ中不同的节点具有不同的阈值概率 P r(SIR(o,x)≥τ),即非均匀分布。因此,随机测度Λ(·)可以表示为
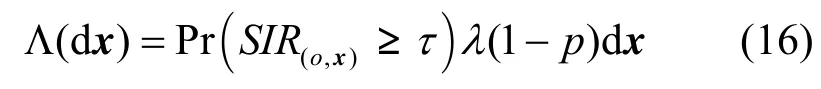
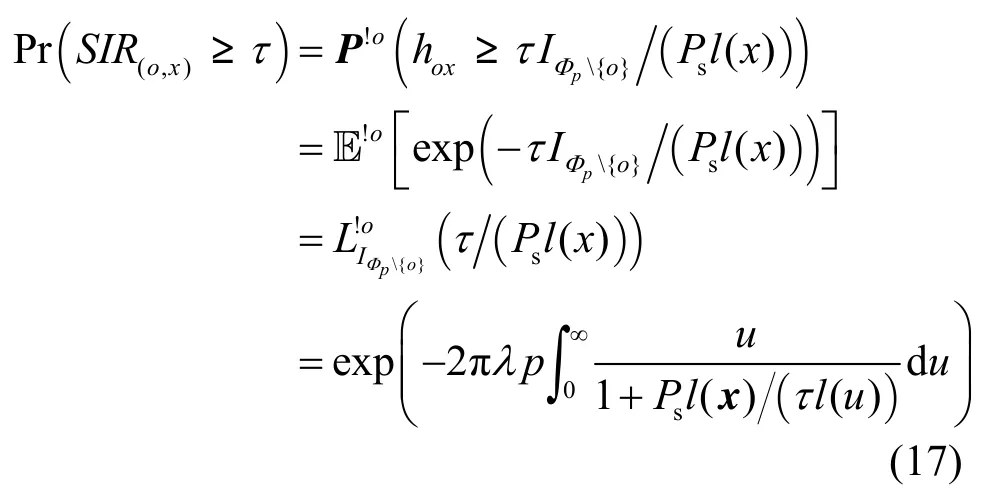
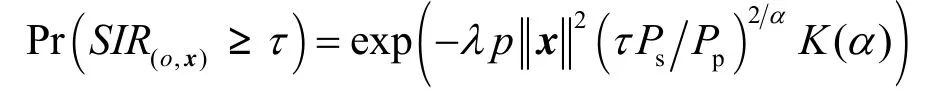
其中,
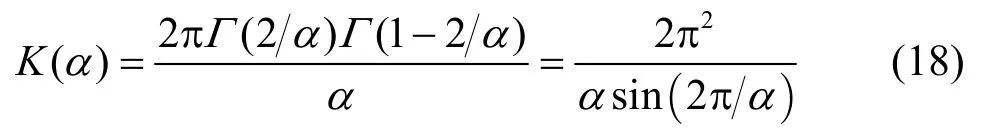
虚拟MIMO信号的CCDF表达式为
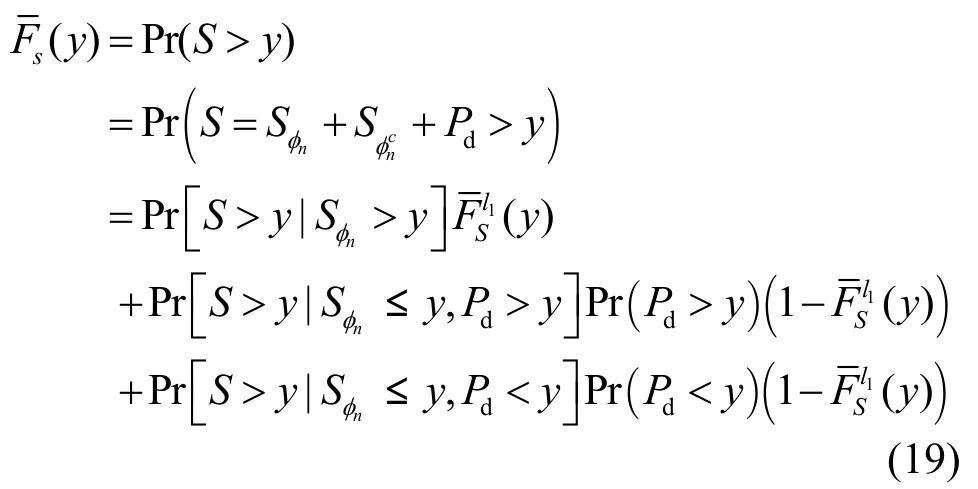
利用Chernoff界,可得
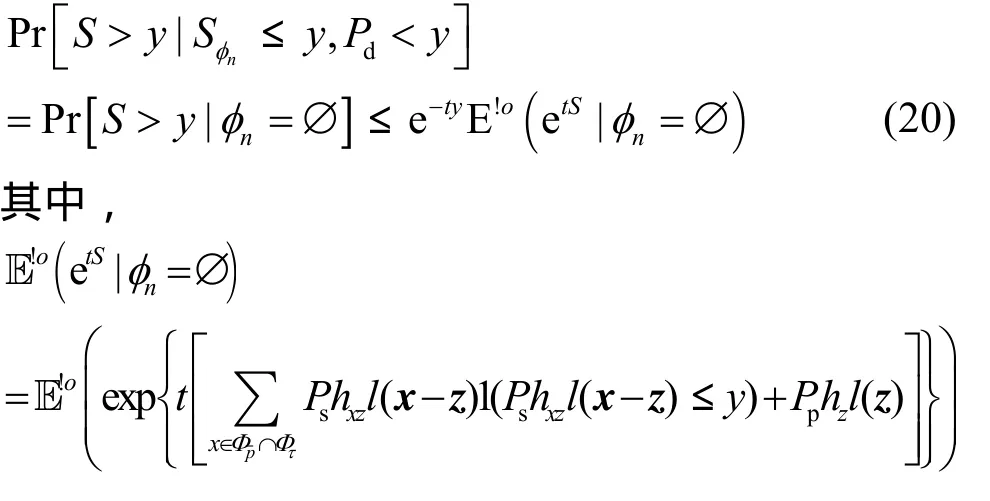
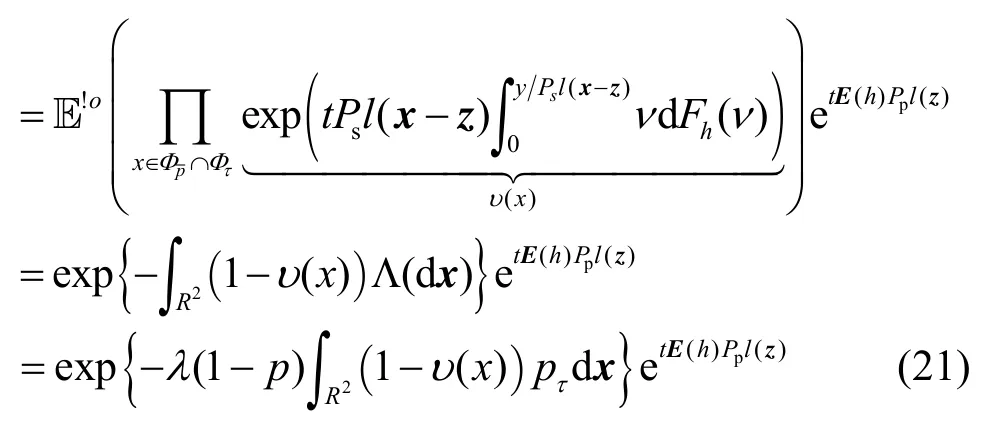
因此,式(20)可以写为
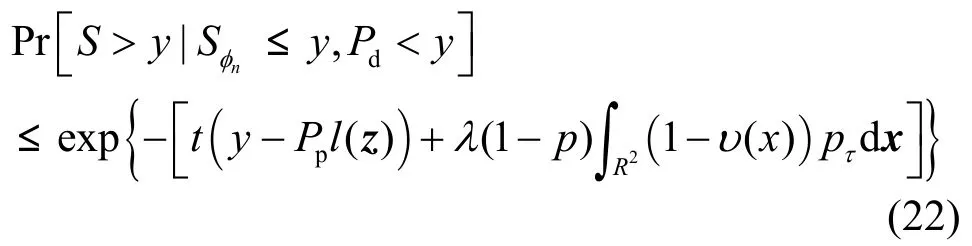
根据式(19)和式(22),上界(y)为
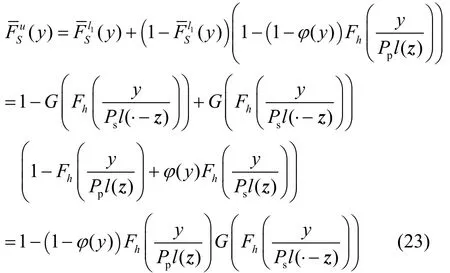
其中,
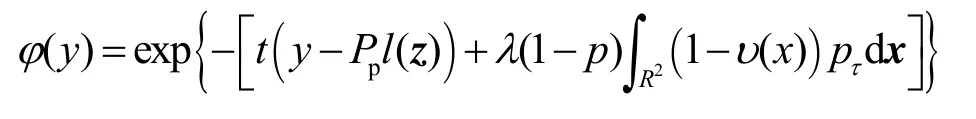
定理1证毕。
推论 1 假设信道为单位方差的瑞利衰落且l(x)=| |x||-α,虚拟MIMO信号的CCDF上下界的渐进分布(当y→∞时)相同。
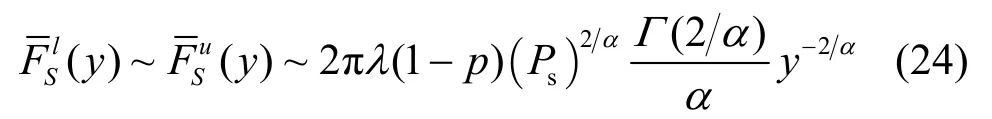
证明 显然,在瑞利衰落信道下式(13)中(y)趋于0的速率远远大于(y)。因此,(y)与(y)具有相同的渐进分布(y→∞),分布特性如下:
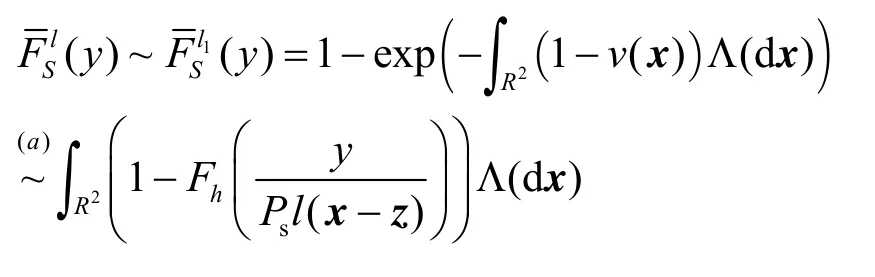
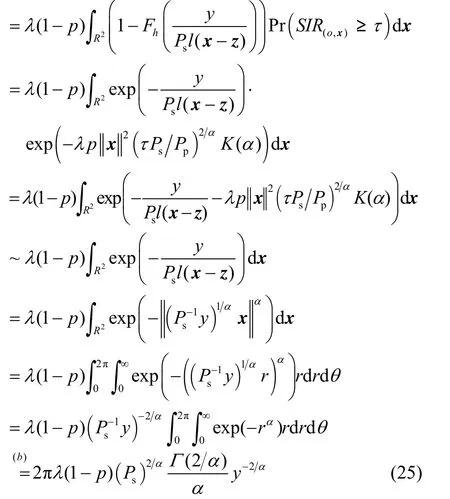
(a)根据1 e~xx-- , 0x→ 。(b)基于
φ(y)的渐进分布为,因为当y→∞时,υ(x)中的积分项趋于常数且得到 CCDF上界的渐进分布:
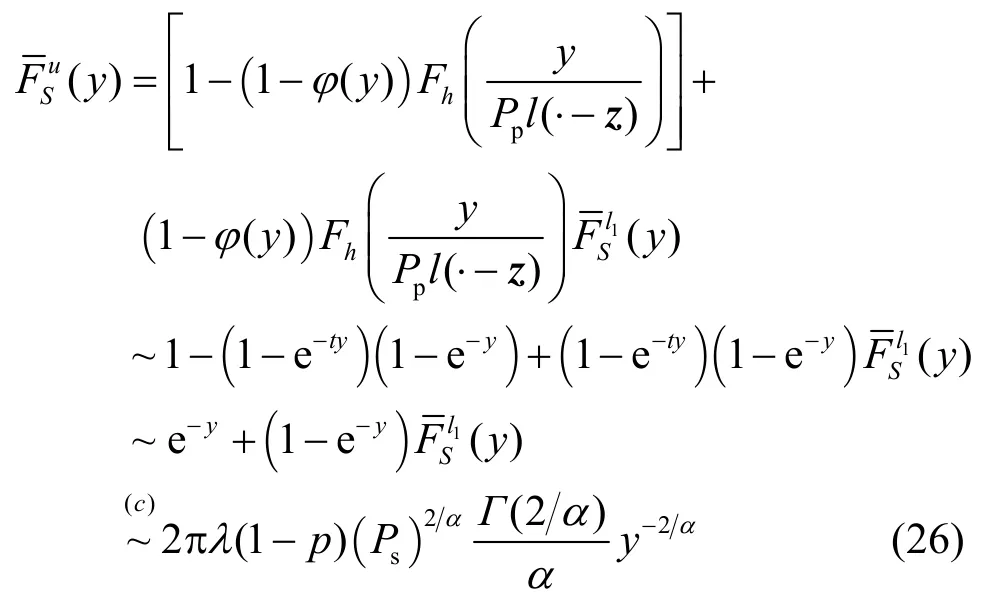
(c)成立因为e-y渐进趋于 0的速率远远大于y-2α。式(25)和式(26)表明虚拟MIMO信号的CCDF上下界具有相同的渐进分布,因此推论1渐进紧致。
推论1证毕。
图3显示了在从用户密度λ(lamda) = 0.5,0.1时的虚拟MIMO信号Monte Carlo仿真及上下界,其中,Pp= 2 ,Ps= 1。可以看到当阈值y增大时,上下界是紧致的,且定理1中的上界优于Markov上界[6]。事实上,在瑞利衰落信道且l(x)=| |x||-α条件下,参与协同的从用户数可以表示为
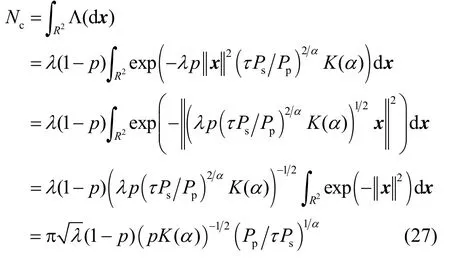
由于参与协同的从用户节点数随着空间密度增大而增多,虚拟MIMO信号的CCDF分布具有较大的拖尾,即从用户干扰增大时主用户信号衰减较慢,有利于信号的传输。
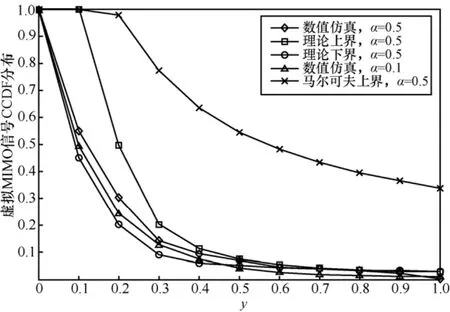
图3 虚拟MIMO信号的仿真及上下界比较
定理 2 当从用户发送节点为空间密度是λ的均匀泊松点过程时,假设节点发送数据概率为p,条件生成函数为G,系统干扰的互补累积分布函数:的下界是上界是
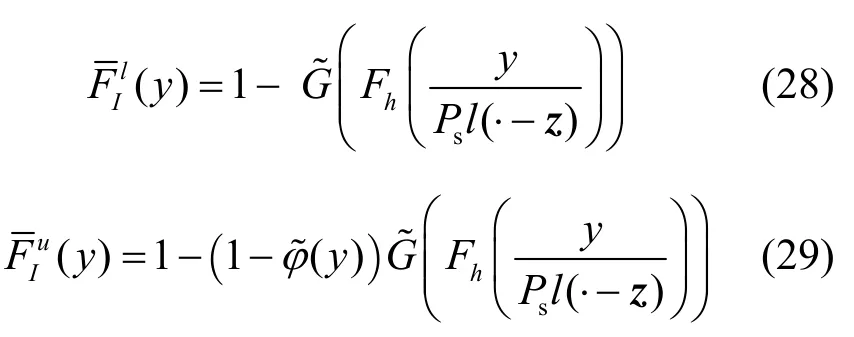
其中,(·)是pΦ的PGFL函数,
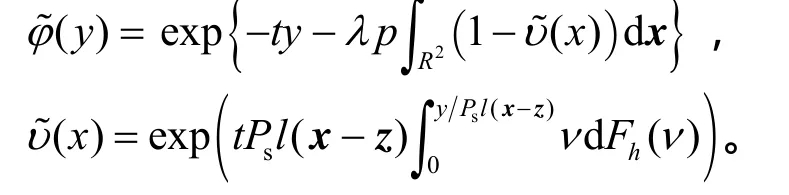
推论 2 假设信道为单位方差的瑞利衰落且l(x)=| |x||-α,主用户受到的干扰CCDF上下界的渐进分布(当y→∞时)相同。
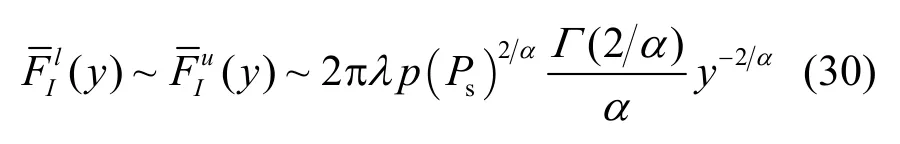
证明方法与推论1相同。
从推论1,2可以看出当p=0.5时虚拟MIMO信号与干扰具有相同的渐进分布,即采用虚拟MIMO技术可以大大提高信号的抗干扰能力。
4 结束语
本文提出了在认知网络中主从用户利用虚拟MIMO技术的协作方案,推导了虚拟MIMO信号及主用户所受干扰的CCDF上下界及其渐进分布表达式,证明了其上下界具有相同的渐进分布。这些结论能够用于估计网络中主从用户最大的传输容量。
[1] LANEMAN J, TSE D, WORNELL G. Cooperative diversity in wireless networks: efficient protocols and outage behavior[J]. IEEE Trans Inf Theory, 2004, 50(12): 3062-3080.
[2] SADEK A, SU W, LIU K. Multinode cooperative communications in wireless networks[J]. IEEE Trans Signal Process, 2007, 55(1): 341-355.
[3] QU Q, MILSTEIN L, VAMAN D. Cooperative and constrained MIMO communications in wireless ad hoc/sensor networks[J]. IEEE Trans Wirel Commun, 2010, 9(10): 3120-3129.
[4] WEBER S, YANG X, ANDREWS J. Transmission capacity of wireless ad hoc networks with outage constraints[J].IEEE Trans Inf Theory, 2005, 51(12):4091-4102.
[5] HAENGGI M, GANTI R. Interference in large wireless networks[J].Foundations and Trends in Networking, 2008, 3(2): 127-248.
[6] GANTI R, HAENGGI M. Interference and outage in clustered wireless ad hoc networks[J].IEEE Trans Inf Theory, 2009, 55(9):4067-4086.
[7] STOYAN D, KENDALL W, MECKE J. Stochastic Geometry and Its Applications[M]. New York: Wiley, 1995.
[8] GRADSHTEYN I, RYZHIK I. Table of Integrals, Series and Products[M]. London, UK: Elsevier Academic Press, 2007.
